Celebratio Mathematica

The A-B slice prob­lem is a for­mu­la­tion of the 4-di­men­sion­al to­po­lo­gic­al sur­gery con­jec­ture, the main open prob­lem re­main­ing in the geo­met­ric clas­si­fic­a­tion the­ory of to­po­lo­gic­al 4-man­i­folds since Mike Freed­man’s fam­ous proof in the simply con­nec­ted case [1]. He also showed that sur­gery works for fun­da­ment­al groups of poly­no­mi­al growth [2]. Since the early 1980s, the class of groups for which sur­gery is known to hold (“good groups”) has been ex­ten­ded some­what to groups of subex­po­nen­tial growth [6], [e2]. The class of good groups is closed un­der the op­er­a­tions of tak­ing sub­groups, ex­ten­sions and dir­ect lim­its, and all cur­rently known good groups are amen­able.

The con­jec­ture of Mike [2], dat­ing back to 1983, as­serts that sur­gery fails for non-Abeli­an free groups. It is not dif­fi­cult to see that the valid­ity of sur­gery for free groups would in fact im­ply valid­ity for all groups. In­deed, the ques­tion is wheth­er a giv­en sur­gery ker­nel — a hy­per­bol­ic pair \( \bigl(\begin{smallmatrix} 0&1\\ 1&0 \end{smallmatrix} \bigr) \) in \( {\pi}_2(M^4) \) — may be rep­res­en­ted by em­bed­ded spheres in­ter­sect­ing in a single point. The al­geb­ra­ic in­ter­sec­tion num­bers are coun­ted in \( {\mathbb Z}[{\pi}_1] \), so geo­met­ric­ally the start­ing data is a pair of im­mersed 2-spheres in a 4-man­i­fold \( M \), whose self-in­ter­sec­tions and ex­tra in­ter­sec­tions are paired up so that the Whit­ney loops are trivi­al in \( {\pi}_1(M) \). A reg­u­lar neigh­bor­hood \( N \) of the 2-com­plex giv­en by the 2-spheres to­geth­er with the Whit­ney disks is it­self a sur­gery prob­lem with free fun­da­ment­al group; clearly, solv­ing all “ca­non­ic­al” prob­lems \( N \) con­struc­ted in this way would im­ply a solu­tion of an ar­bit­rary sur­gery prob­lem.

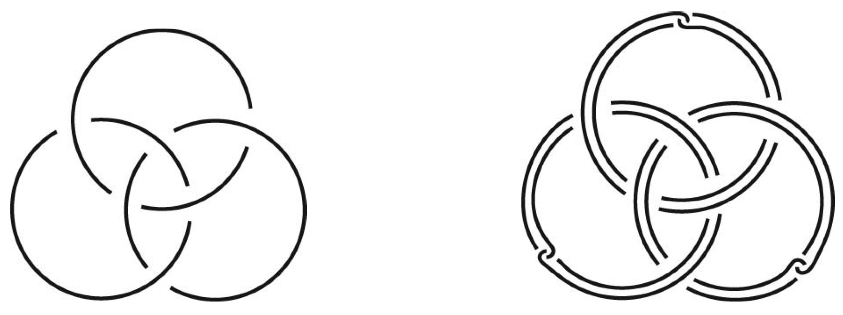
An­oth­er col­lec­tion of ca­non­ic­al sur­gery prob­lems is con­struc­ted as fol­lows: Con­sider the Bor­romean rings (and more gen­er­ally the fam­ily of links giv­en by it­er­ated Bing doub­lings of the Hopf link, where one can also take par­al­lel cop­ies of the com­pon­ents at each stage of the it­er­a­tion). Then, the sur­gery con­jec­ture is equi­val­ent to the ques­tion of wheth­er the un­twis­ted White­head doubles of the links in this col­lec­tion (Fig­ure 1) are freely slice. Here, a link is freely slice if it is to­po­lo­gic­ally slice, and moreover the fun­da­ment­al group of the slice com­ple­ment in \( \mathbb D^4 \) is freely gen­er­ated by me­ridi­ans to the slices. Con­sid­er­ing the slice com­ple­ment, one ob­serves that this ques­tion (say, for the simplest link in this col­lec­tion, pic­tured in Fig­ure 1 is equi­val­ent to the ex­ist­ence of a to­po­lo­gic­al 4-man­i­fold \( M \) ho­mo­topy equi­val­ent to the wedge of three circles and whose bound­ary is giv­en by the zero-framed sur­gery on the White­head double of the Bor­romean rings, \( \mathrm{Wh}(\mathit{Bor}) \). Mike’s con­jec­ture [2] is that such \( M \) does not ex­ist; prov­ing this would ex­hib­it a counter­example of the sur­gery con­jec­ture.

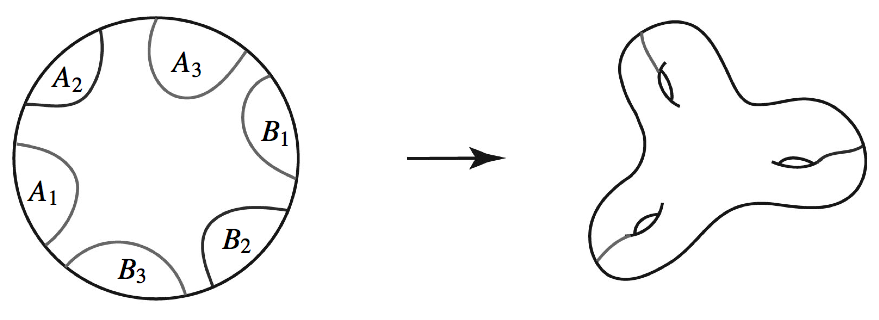
In [3], [4] Mike in­tro­duced an ap­proach to this con­jec­ture, known as the A-B slice prob­lem. This ap­proach re­places the slice prob­lem for a very “weak” link \( \mathrm{Wh}(\mathit{Bor}) \) by a gen­er­al­ized slice prob­lem for a much more “ro­bust” link, the Bor­romean rings. More con­cretely, sup­pose the hy­po­thet­ic­al 4-man­i­fold \( M \), dis­cussed above, ex­ists. Then, con­sider its uni­ver­sal cov­er \( \widetilde M \). It is shown in [3] that the end-point com­pac­ti­fic­a­tion of \( \widetilde M \) is homeo­morph­ic to the 4-ball. The group of cov­er­ing trans­form­a­tions (the free group on three gen­er­at­ors) acts on \( \mathbb D^4 \) with a pre­scribed ac­tion on the bound­ary, and roughly speak­ing the A-B slice prob­lem is a pro­gram for find­ing an ob­struc­tion to the ex­ist­ence of such ac­tions. Fig­ure 2 il­lus­trates a fun­da­ment­al do­main for this ac­tion on \( \mathbb D^4 \) where, for each \( i=1,2,3 \), the free gen­er­at­or \( g_i \) of the cov­er­ing trans­la­tion group takes \( A_i \) to the com­ple­ment \( \mathbb D^4\smallsetminus B_i \).

To de­scribe the prob­lem in more de­tail, con­sider de­com­pos­i­tions \( \mathbb D^4=A\cup B \) of the 4-ball in­to two codi­men­sion-zero smooth sub­man­i­folds \( A \) and \( B \), ex­tend­ing the stand­ard genus-one Hee­gaard de­com­pos­i­tion of the 3-sphere, \( \partial\mathbb D^4=\mathbb S^1\times\mathbb D^2\,\cup\,\mathbb D^2\times\mathbb S^1 \). The com­pon­ents of the Hopf link \( \mathbb S^1\times 0\,\sqcup\, 0 \times \mathbb S^1 \) are thought of as the “at­tach­ing curves” of \( A \) and \( B \). The sub­man­i­folds \( A \) and \( B \) are dis­joint ex­cept for their bound­ary.

An \( n \)-com­pon­ent link \( L \) is A-B slice if there ex­ist \( n \) de­com­pos­i­tions of the 4-ball, \( \mathbb D^4=A_i\cup B_i \) for \( i=1,\ldots, n \), and dis­joint em­bed­dings of all \( 2n \) pieces \( \{A_i, B_i\} \) in­to \( \mathbb D^4 \) so that the at­tach­ing curves of the \( \{ A_i\} \) form the link \( L \), and the at­tach­ing curves of the \( \{ B_i\} \) form a par­al­lel copy of \( L \). Moreover, the cov­er­ing group ac­tion is en­coded in the fur­ther re­quire­ment that each one of the em­bed­dings of \( A_i, B_i \) is iso­top­ic to the ori­gin­al em­bed­ding, which is spe­cified by the de­com­pos­i­tion \( \mathbb D^4=A_i\cup B_i \).

There­fore, the sur­gery con­jec­ture is re­for­mu­lated in­to the ques­tion of wheth­er the Bor­romean rings (and a fam­ily of their gen­er­al­iz­a­tions, dis­cussed above) are A-B slice. An easy ar­gu­ment, us­ing Al­ex­an­der du­al­ity, im­plies that the Hopf link is not A-B slice, and one is led to be­lieve that a vari­ant of such an ar­gu­ment us­ing Mil­nor’s \( \bar\mu \)-in­vari­ants [e1] would give an ob­struc­tion for the Bor­romean rings as well. However, the step from the link­ing num­ber to \( \bar\mu_{123} \) turns out to be chal­len­ging. A par­tic­u­lar is­sue that comes up is the in­de­term­in­acy of the high­er Mil­nor’s in­vari­ants; while usu­ally it is not hard to ana­lyze spe­cif­ic giv­en ex­amples of de­com­pos­i­tions, it has been hard to for­mu­late an in­vari­ant work­ing uni­formly for all de­com­pos­i­tions.

The A-B slice ap­proach to sur­gery was fur­ther de­veloped in Mike’s joint pa­per with Xiao-Song Lin [5]. This pa­per in­tro­duced a col­lec­tion of mod­el de­com­pos­i­tions that ap­peared to ap­prox­im­ate, in a cer­tain al­geb­ra­ic sense, an ar­bit­rary de­com­pos­i­tion \( \mathbb D^4=A\cup B \). It seemed reas­on­able to think then that, if a suit­able ob­struc­tion is for­mu­lated for these mod­els, one should be able to ex­tend it to all de­com­pos­i­tions. [5] also de­veloped the re­l­at­ive-slice re­for­mu­la­tion of the prob­lem, use­ful in par­tic­u­lar for ana­lyz­ing spe­cif­ic ex­amples of de­com­pos­i­tions.

Us­ing a gen­er­al­iz­a­tion of the Mil­nor group, an ob­struc­tion was giv­en for mod­el de­com­pos­i­tions in [e3]. A subtle phe­nomen­on was ob­served in [e4] which showed that there ex­ist de­com­pos­i­tions \( \mathbb D^4=A_i\cup B_i \) and dis­joint em­bed­dings of the six pieces in the 4-ball with the re­quired bound­ary con­di­tions, there­fore es­tab­lish­ing that the Bor­romean rings are weakly A-B slice. This dis­proved a stronger ver­sion of the con­jec­ture of Mike, stated in [5]; however, these ex­amples do not solve the A-B slice prob­lem in the af­firm­at­ive, be­cause the equivari­ance con­di­tion is not sat­is­fied: the re-em­bed­dings of \( A_i, B_i \) are not stand­ard (that is, are not iso­top­ic to the ori­gin­al ones).

More re­cently, the no­tion of to­po­lo­gic­al ar­bit­ers was stud­ied in [7]. A to­po­lo­gic­al ar­bit­er is an in­vari­ant which as­signs either 0 or 1 to each side \( A, B \) of any de­com­pos­i­tion, sub­ject to cer­tain nat­ur­al ax­ioms. In par­tic­u­lar, it is a to­po­lo­gic­al in­vari­ant, and the val­ues as­so­ci­ated to the two sides of a de­com­pos­i­tion are re­quired to be dif­fer­ent. The no­tion of a to­po­lo­gic­al ar­bit­er, to­geth­er with an ad­di­tion­al “Bing doub­ling” prop­erty, ax­io­mat­ize the prop­er­ties that an ob­struc­tion to the A-B slice prob­lem should sat­is­fy. [7] proved the ex­ist­ence of an un­count­able col­lec­tion of to­po­lo­gic­al ar­bit­ers in di­men­sion 4, but the ex­ist­ence of one also sat­is­fy­ing the Bing-doub­ling ax­iom re­mains an open ques­tion.