Celebratio Mathematica

Most math­em­aticians can­not define the spaces of al­geb­ra­ic geo­metry, called schemes, off the top of their heads, nor the morph­isms \( f:S \to S^{\prime} \) map­ping one scheme al­gebro-geo­met­ric­ally to an­oth­er. But they can define the cartesian product \( S \times S^{\prime} \) and the cop­roduct, or uni­on, \( S \cup S^{\prime} \) of schemes (up to iso­morph­ism) by fa­mil­i­ar dia­grams of morph­isms, as in the fig­ure.

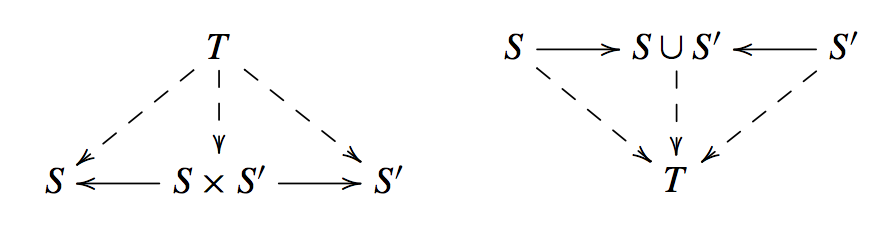
Mac Lane wrote two auto­bi­o­graph­ies. Ob­vi­ously there is his Math­em­at­ic­al Auto­bi­o­graphy [38]. Less ob­vi­ous is Math­em­at­ics: Form and Func­tion [23], aimed at philo­soph­ers. It sur­veys the math­em­at­ics Mac Lane wanted philo­soph­ers to know. Nat­ur­ally, that is the math­em­at­ics Mac Lane wanted to know over the years, so this sweep­ing sur­vey is little more sweep­ing than his own ca­reer. Hav­ing at­ten­ded lec­tures by Dav­id Hil­bert and Emmy No­eth­er, and stud­ied with Paul Bernays and Her­mann Weyl, Mac Lane made noted con­tri­bu­tions to al­gebra, to­po­logy and group the­ory. He was in­flu­en­tial in lo­gic. He pub­lished on geo­metry, mech­an­ics and on teach­ing cal­cu­lus. He looked over the whole scope of math­em­at­ics as vice pres­id­ent of the Na­tion­al Academy of Sci­ences and the Amer­ic­an Philo­soph­ic­al So­ci­ety.2 He was pres­id­ent of the Math­em­at­ic­al As­so­ci­ation of Amer­ica and the Amer­ic­an Math­em­at­ic­al So­ci­ety, and chair of Math­em­at­ics at Chica­go from 1952 to 1958, where the math­em­at­ics de­part­ment was com­pet­ing to be the strongest in the world.

His cent­ral achieve­ment was the co-cre­ation, with Samuel Ei­len­berg, of cat­egory the­ory, which be­came the way math­em­aticians or­gan­ize each branch of math­em­at­ics and es­pe­cially the re­la­tions between branches. Math­em­at­ics: Form and Func­tion comes sur­pris­ingly close to re­peat­ing, in chro­no­lo­gic­al or­der, his own math­em­at­ic­al in­terests. It de­vel­ops a philo­sophy already re­cog­niz­able in his Journ­al of Sym­bol­ic Lo­gic re­views in the 1930s and 1940s, yet which fi­nally re­lied on Wil­li­am Lawvere’s cat­egor­ic­al found­a­tions ([e18], [e8]).

Mac Lane was dis­tinct­ively Amer­ic­an. His out­look was cos­mo­pol­it­an and pro­gress­ive. His trade­mark Mac Lane tartan suit showed his ex­uber­ant pride in his im­mig­rant fam­ily past. He traced his in­tel­lec­tu­al roots to a Pres­by­teri­an grand­fath­er “of­fi­cially charged with heresy for preach­ing on the writ­ings of Charles Dar­win” in Ohio in 1883 ([38], p. 3).3 In many ways his ca­reer fol­lowed that of Eliakim Hast­ings Moore (1862–1932), who set out to make Amer­ica a world force in math­em­at­ics.

Re­tired but still teach­ing, Pro­fess­or Moore made a tre­mend­ous im­pres­sion on the be­gin­ning gradu­ate stu­dent ([38], p. 36). Both had stud­ied at Yale. Moore stud­ied in Ger­many and headed the math­em­at­ics de­part­ment at Chica­go from the time the uni­versity first opened in 1892. Mac Lane went to Göttin­gen for his doc­tor­ate in 1931 and later headed the de­part­ment at Chica­go. Both were lead­ers in the re­search-ori­ented Amer­ic­an Math­em­at­ic­al So­ci­ety. Moore’s in­terest in math­em­at­ics edu­ca­tion made him a co-founder of the Math­em­at­ic­al As­so­ci­ation of Amer­ica to com­ple­ment the AMS. As pres­id­ent of the MAA in the 1950s, Mac Lane worked to up­date math­em­at­ics teach­ing. Moore was the doc­tor­al teach­er of G. D. Birk­hoff, fath­er of Gar­rett Birk­hoff who co-au­thored [9] and [16]. And Moore had a prin­ciple:

The ex­ist­ence of ana­lo­gies between cent­ral fea­tures of vari­ous the­or­ies im­plies the ex­ist­ence of a gen­er­al ab­stract the­ory which un­der­lies the par­tic­u­lar the­or­ies and uni­fies them with re­spect to those cent­ral fea­tures. ([e2], p. 98)

Cat­egory the­ory was cre­ated to find the unity be­hind deep ana­lo­gies between to­po­logy and al­gebra. Today it is a stand­ard format for giv­ing such “gen­er­al ab­stract” the­or­ies. Con­sid­er­a­tion of the re­la­tion of Moore to Mac Lane would re­pay far more at­ten­tion than it has got­ten.4 Study­ing lo­gic in Göttin­gen from 1931 to 1933, right after Gödel’s in­com­plete­ness the­or­em, Mac Lane de­veloped a strong feel­ing for Hil­bert’s “form­al­ism.” He had an ex­change in the New York Re­view of Books with Free­man Dys­on on the point. Dys­on claimed Hil­bert had gone “in­to a blind al­ley of re­duc­tion­ism … re­du­cing math­em­at­ics to a set of marks writ­ten on pa­per, and de­lib­er­ately ig­nor­ing the con­text of ideas and ap­plic­a­tions that give mean­ing to the marks.” Mac Lane said to the con­trary that Hil­bert meant quite con­crete math­em­at­ic­al know­ledge in his fam­ous slo­gan Wir müssen wis­sen; wir wer­den wis­sen (We must know, we will know): “This was the tone of his gen­er­al lec­ture course on the philo­sophy of sci­ence which I heard him give in late 1931.” Hil­bert used form­al­iz­a­tion in its own prop­er do­main:

Hil­bert him­self called this “metamathem­at­ics.” He used this for a spe­cif­ic lim­ited pur­pose, to show math­em­at­ics con­sist­ent. Without this re­duc­tion, no Gödel’s the­or­em, no defin­i­tion of com­put­ab­il­ity, no Tur­ing ma­chine, and hence no com­puters.

Dys­on simply does not un­der­stand re­duc­tion­ism and the deep pur­poses it can serve. Hil­bert was not “sterile.”

Dys­on fi­nally agreed with him about Hil­bert and said “Hil­bert him­self was, of course, a mas­ter of both [form­al and con­crete] kinds of math­em­at­ics,” but oddly Dys­on would not ex­tend the same con­ces­sion to Mac Lane. He in­sisted Mac Lane “is by tem­pera­ment a re­duc­tion­ist.” In fact, Mac Lane was no kind of re­duc­tion­ist. He saw what form­al­iz­a­tion could achieve while he was con­stantly in­volved with the ideas and ap­plic­a­tions that give it mean­ing.5 The spe­cif­ic pro­ject of his Göttin­gen dis­ser­ta­tion was to give form­al means of ab­bre­vi­at­ing form­al proofs. But the lar­ger goal was to bring form­al lo­gic closer to prac­tice and make it ex­press more dir­ectly how

A proof is not just a series of in­di­vidu­al steps, but a group of steps, brought to­geth­er ac­cord­ing to a def­in­ite plan or pur­pose …. So we af­firm that every math­em­at­ic­al proof has a lead­ing idea, which de­term­ines all the in­di­vidu­al steps, and can be giv­en as a plan of the proof. ([1], p. 60)

This lar­ger pro­ject be­came a philo­soph­ic­al art­icle in the Mon­ist the year that Mac Lane star­ted pub­lish­ing [2]. It is re­af­firmed, for ex­ample, in [35].

Mac Lane’s most pen­et­rat­ing work in math­em­at­ics, philo­sophy and his­tory of math­em­at­ics came from his en­counter with Emmy No­eth­er in Göttin­gen. He went there for Hil­bert’s lo­gic and be­cause Øys­tein Ore at Yale had told him of No­eth­er, who was yet little known in the U.S. He had trouble ab­sorb­ing her ideas on factor sets and crossed products, which re­placed massive amounts of cal­cu­la­tion in num­ber the­ory with sharp con­cep­tu­al ar­gu­ments, al­though he notes that “they still in­volve heavy com­pu­ta­tion.”6 Mac Lane al­ways said that a math­em­atician needs to keep prac­ticed at long cal­cu­la­tion. Over time, Mac Lane cla­ri­fied factor sets and crossed products by a yet tight­er con­cep­tu­al frame­work: group co­homo­logy. No­eth­er’s uni­fic­a­tion of arith­met­ic and ab­stract al­gebra be­came a uni­fic­a­tion of group the­ory and to­po­logy in a thor­oughly cat­egor­ic­al way. He later wrote his­tor­ic­al ex­pos­it­ory art­icles with philo­soph­ic in­vest­ig­a­tion of cre­ation and con­cep­tu­al­iz­a­tion, al­gebra and geo­metry.7 These ideas are om­ni­present in ad­vanced num­ber the­ory today, in the form of their des­cend­ants Galois co­homo­logy, étale co­homo­logy and oth­ers; see, e.g., [e15].

Mac Lane’s most sus­tained ped­ago­gic­al ef­fort began with No­eth­er as well. That was the 25 year evol­u­tion of his al­gebra text­book with Birk­hoff. First [9] was an Amer­ic­an take on the No­eth­er school of al­gebra. Even­tu­ally [16] be­came many stu­dents’ first look at cat­egor­ic­al math­em­at­ics.8 Göttin­gen is also the reas­on, though, that philo­soph­ers today have trouble read­ing Mac Lane, es­pe­cially his Math­em­at­ics: Form and Func­tion. He pur­sued philo­sophy at length with Her­mann Weyl and worked on re­vis­ing [e3]. As part of his D. Phil. de­gree, he stud­ied philo­sophy of math­em­at­ics with phe­nomen­o­lo­gist and Hil­bert dis­ciple Mor­itz Gei­ger.9 For Göttin­gen math­em­aticians at that time, philo­sophy was phe­nomen­o­logy. This phe­nomen­o­logy came from Ed­mund Husserl, who had trained in math­em­at­ics with Karl Wei­er­strass and Leo­pold Kro­neck­er and whose doc­tor­al dis­ser­ta­tion was on cal­cu­lus of vari­ations. Hil­bert got him hired in philo­sophy at Göttin­gen.10 At Har­vard, from the mid-1930s to 1947, Mac Lane spoke of­ten with Wil­lard Quine but re­jec­ted Quine’s “un­due con­cern with lo­gic, as such.” ([23], p. 443) Mac Lane would ab­sorb a good dose of Karl Pop­per. But his base note would re­main 1930s Göttin­gen phe­nomen­o­logy — the philo­sophy of math­em­aticians.

Phe­nomen­o­lo­gists ac­cept many dif­fer­ent at­ti­tudes to­wards be­ing. Gei­ger es­pe­cially de­scribes the “nat­ur­al­ist­ic at­ti­tude,” which re­duces everything to phys­ic­al ex­ist­ence, the “im­me­di­ate at­ti­tude,” which re­cog­nizes so­cial ex­ist­ence (as of a poem or a law), psych­ic ex­ist­ence (as of a feel­ing or per­cep­tion) and more. None of these is right or wrong for Gei­ger; rather each has its role in life. At times they com­pete for a role. He says some people take a nat­ur­al­ist­ic at­ti­tude to­wards lo­gic and thus re­duce it to a branch of psy­cho­logy, which he finds mis­taken. For Gei­ger, math­em­at­ics can only be un­der­stood in the im­me­di­ate at­ti­tude. Its ob­jects ex­ist as forms (Gestal­ten, Ge­bilde), which may be forms of phys­ic­al ob­jects but are not them­selves phys­ic­ally real ([e4], esp. pp. 82, 86–88, 115).

Thus for Mac Lane, math­em­at­ics stud­ies forms or as­pects, which can be ap­plied to study phys­ic­ally real things. All of the Eu­c­lidean and non-Eu­c­lidean geo­met­ries can be ap­plied to phys­ic­al space by suit­able defin­i­tions of “dis­tance.” Which one best suits phys­ics is not a math­em­at­ic­al ques­tion. Math­em­at­ic­al state­ments may be proved or not, il­lu­min­at­ing or not, but they can­not be true or false, be­cause they are not em­pir­ic­ally falsifi­able. So math­em­at­ics makes no on­to­lo­gic­al com­mit­ments. Mac Lane nev­er be­came a Quinean, far less a post-Hil­ary Put­nam Quinean.11

Back in the 1930s, re­turned from Ger­many, Mac Lane fo­cussed on al­gebra be­cause it was hard to get a job in lo­gic ([38], p. 62). He joined the As­so­ci­ation for Sym­bol­ic Lo­gic and wrote a sur­vey of top­ics in lo­gic for dis­cus­sion in math clubs [5]. His lo­gic and philo­sophy are scattered, of­ten in re­views. He shows far more know­ledge of proof the­ory in [3] than in his 1934 dis­ser­ta­tion. He re­views many ideas on the found­a­tions of math­em­at­ics in his [8] and [11].12 He en­dorses Church:

This is an up-to-date de­scrip­tion of the cent­ral prob­lem in the found­a­tions of math­em­at­ics. This prob­lem is taken to be “the con­struc­tion of a sym­bol­ic sys­tem with­in which the body of ex­tant math­em­at­ics may be de­rived in ac­cord­ance with sharply stated and im­me­di­ately ap­plic­able form­al rules.” Oth­er prob­lems, con­nec­ted with the ul­ti­mate nature of math­em­at­ics or with the pos­sible char­ac­ter­iz­a­tion of math­em­at­ics as a branch of form­al lo­gic, must wait on this cent­ral prob­lem for solu­tion. [8]

Mac Lane, too, was un­sat­is­fied with ex­ist­ing set the­or­ies. He would much later re­peat “there is yet no simple and ad­equate way of con­cep­tu­ally or­gan­iz­ing all of Math­em­at­ics” though he con­sidered cat­egor­ic­al found­a­tions the best pro­spect and he no longer saw this is­sue as pri­or to all oth­ers ([23], p. 407).

He treated themes that would re­appear after he met Lawvere. Mar­shall Stone “shows sur­pris­ing geo­met­ric con­tent in many ap­par­ently purely al­geb­ra­ic or lo­gic­al ideas” in ways topos the­ory would later ex­tend [6], [28]. Work by Tarski does the same [4]. J-L. Destouches pro­poses a “new lo­gic” for phys­ics but:

This cal­cu­lus is sym­bol­ized only in­com­pletely, and tends to con­fuse sys­tem with meta-sys­tem. It is not free from tech­nic­al er­rors …. Any such “new lo­gic” for Phys­ics must re­main a gra­tu­it­ous spec­u­la­tion un­til someone pro­duces such a lo­gic and uses it in Phys­ics in some way not pos­sible for the clas­sic­al lo­gic. [7]

Later he would find that [e11] and re­lated works suc­ceeded at this.

Mac Lane had great fun re­view­ing Eric Temple Bell’s De­vel­op­ment of Math­em­at­ics. His re­view is worth read­ing today for dis­cus­sion of many math­em­at­ic­al ad­vances — and for Mac Lane’s de­fence of the philo­soph­ers: “Is Pla­to as vi­cious as Bell’s every­where dense cracks would in­dic­ate? … The philo­soph­er will dis­agree with the jabs at Kant.” It dis­cusses am­bi­gu­ities in the idea of “struc­ture.” And it con­veys Mac Lane’s ap­proach to every ac­count of math­em­at­ics and its philo­sophy: “don’t won­der about it, but go, read, and dis­agree for your­self” [13].

From 1944 to 1948, Mac Lane was on the Coun­cil of the As­so­ci­ation for Sym­bol­ic Lo­gic. Around that time, as ed­it­or of the Carus Math­em­at­ic­al Mono­graphs, he urged Steph­en Kleene and Barkley Ross­er to write on lo­gic. “In Kleene’s case this led to the pre­par­a­tion of his mag­ni­fic­ant volume In­tro­duc­tion to Metamathem­at­ics.” ([31], p. 4)13 He be­came the Ph.D. ad­visor to lo­gi­cians Wil­li­am Howard, Mi­chael Mor­ley, Anil Ner­ode, Robert So­lovay and Steven Awodey.

His math­em­at­ics stayed in touch with found­a­tions. The found­ing pa­per of cat­egory the­ory made a start­ling claim.14 While giv­ing trivi­al ex­amples from lin­ear al­gebra, and deep ap­plic­a­tions to ex­tremely ad­vanced to­po­logy, Ei­len­berg and Mac Lane say:

In a metamathem­at­ic­al sense our the­ory provides gen­er­al con­cepts ap­plic­able to all branches of math­em­at­ics, and so con­trib­utes to the cur­rent trend to­wards uni­form treat­ment of dif­fer­ent math­em­at­ic­al dis­cip­lines. ([12], p. 236)

The pa­per also gives sev­er­al strategies for the set-the­or­et­ic prob­lems posed by large cat­egor­ies ([12], p. 246).

The great math­em­at­ic­al de­bate over cat­egory the­ory took place in private over the next few years, in­deed in closed meet­ings of the Bourbaki group, with Ei­len­berg a mem­ber and Mac Lane some­times vis­it­ing. He was pho­to­graphed at one ([e17], p. 85). Cat­egory the­ory lost in de­bate and won in prac­tice. Bourbaki for­mu­lated a set-the­or­et­ic no­tion of “struc­ture” as basis for their en­cyc­lo­ped­ic Ele­ments of Math­em­at­ics [e6], yet even their own later volumes nev­er use this the­ory. Mem­bers who re­lied on (and in­ven­ted much) cat­egory the­ory in their work were bit­terly dis­ap­poin­ted.15 Bourbaki struc­tures are something like Tarski mod­els.16 Mac Lane made at least one ef­fort to deal with “struc­tures” in this sense since it is fa­mil­i­ar to philo­soph­ers [32]. But com­pare [23], p. 33, where these are called sets-with-struc­ture and treated as im­port­ant ex­amples but not the only kind of “struc­ture.” He could nev­er really en­gage with ver­sions of “struc­tur­al­ism” which neg­lect the tools math­em­aticians use. To say the least, math­em­aticians handle struc­tures by the morph­isms between them which are neg­lected by philo­soph­ic­al “ struc­tur­al­ists.” To say the truth, math­em­aticians handle morph­isms by cat­egory the­ory.

His en­counter with Lawvere brought Mac Lane back to a fo­cus on lo­gic, found­a­tions and philo­sophy of math­em­at­ics.17 When he first heard of Lawvere’s ideas on set the­ory, which be­came the Ele­ment­ary the­ory of the cat­egory of sets or ETCS for short, he found them en­tirely im­plaus­ible. He found the ax­ioms en­tirely per­suas­ive when he learned them. Un­for­tu­nately, in one of those mis­placed jokes that so com­plic­ate the his­tory of thought, Mac Lane was fond of call­ing ETCS “set the­ory without ele­ments” ([38], at length on p. 192). Set the­ory is no jok­ing mat­ter. A good num­ber of lo­gi­cians have taken him lit­er­ally, not­with­stand­ing that ele­ments are defined early in any ac­count of ETCS ([e8], p. 1507). Mac Lane has con­sist­ently backed ETCS as the best work­ing found­a­tion for math­em­at­ics ([37], Ap­pendix).

To philo­soph­ers, though, he says there is no single “found­a­tion” for math­em­at­ics and the pur­por­ted found­a­tions are bet­ter seen as “pro­pos­als for the or­gan­iz­a­tion of Math­em­at­ics” ([23], p. 406). They can­not be “start­ing points” or “jus­ti­fic­a­tions” for math­em­at­ics which is far older and more se­curely known than they are.

Mac Lane had used cat­egory the­ory to sim­pli­fy many as­pects of math­em­at­ics. Lawvere brought a rad­ic­al idea that even the simplest no­tions — such as the nat­ur­al num­bers or sets of func­tions — have simple cat­egor­ic­al ver­sions which could bring found­a­tions closer to nor­mal prac­tice. Found­a­tions could use the very tools that math­em­aticians use daily. Mac Lane jumped onto this pro­gram. He re­garded it as mark­ing a deep shift in the dir­ec­tion of cat­egory the­ory and part of a lar­ger shift away from gen­er­al­ity and to­wards fo­cussed themes in ab­stract al­gebra. See es­pe­cially his [21], [24].

This brings us up to Mac Lane’s first auto­bi­o­graphy, writ­ten “as a back­ground for the philo­sophy of Math­em­at­ics” ([23], back cov­er).18 Like his ca­reer it be­gins with the found­a­tions of al­gebra plus the ba­sic to­po­logy Mac Lane learned from Haus­dorff’s Men­gen­lehre: “the first ser­i­ous math­em­at­ic­al text that I read” ([27], p. 6). It moves to ax­io­mat­ic geo­metry, group the­ory and Galois the­ory, all close to themes of his 1930s re­search; then cal­cu­lus and lin­ear al­gebra which he taught in the 1940s; and then com­plex ana­lys­is and mech­an­ics which he began to teach in the 1950s and 1960s. (I find no trace of his war work in ap­plied math­em­at­ics.) It ends with found­a­tions and philo­sophy. Of course that puts philo­sophy out of or­der. He stud­ied it early and late. The book is not meant to be chro­no­lo­gic­al. It is just such a power­fully, per­son­ally in­formed, view of math­em­at­ics that it nat­ur­ally fol­lows his course. The later auto­bi­o­graphy [38] has great per­son­al de­tail and great math­em­at­ics. In­deed it has more ad­vanced math­em­at­ics than Math­em­at­ics: Form and Func­tion.19 But Math­em­at­ics: Form and Func­tion is what Saun­ders had to say to the philo­soph­ers.

Let him have the last word, from a talk he gave at mid-ca­reer, fifty-one years ago:

It can­not be too of­ten re­it­er­ated that the aim of col­legi­ate math­em­at­ics is the un­der­stand­ing of math­em­at­ic­al ideas per se. The ap­plic­a­tions sup­port the un­der­stand­ing, and not vice versa…

We must con­trive ever anew to ex­pose our stu­dents — be they gen­er­al stu­dents or spe­cial­ized stu­dents — to the beauty and ex­cite­ment and rel­ev­ance of math­em­at­ic­al ideas. We must set forth the ex­traordin­ary way in which math­em­at­ics, spring­ing from the soil of ba­sic hu­man ex­per­i­ence with num­bers and data and space and mo­tion, builds up a far-flung ar­chi­tec­tur­al struc­ture com­posed of the­or­ems which re­veal in­sights in­to the reas­ons be­hind ap­pear­ances and of con­cepts which re­late totally dis­par­ate con­crete ideas…

Math­em­at­ics as it is today … can no longer be presen­ted by piece­meal courses, for it is simply no longer true that ad­vanced math­em­at­ics can be split neatly in­to com­part­ments la­belled “al­gebra,” “ana­lys­is,” “geo­metry,” and “ap­plied math­em­at­ics”…

You may protest that I am talk­ing about re­search and not about edu­ca­tion… I an­swer, first: The char­ac­ter and dir­ec­tion of cur­rent re­search is the best in­dic­a­tion of the ideas which we ought to be teach­ing. I an­swer, second: One of our main re­spons­ib­il­it­ies is that of train­ing the re­search math­em­aticians of the fu­ture. Amer­ic­an Math­em­at­ics has made tre­mend­ous strides [by] the in­fu­sion of European math­em­at­ic­al tal­ent. In the dec­ades to come, we must pro­duce a sim­il­ar in­fu­sion on our own and from our own stu­dents…

The prop­er treat­ment of cal­cu­lus for func­tions of sev­er­al vari­ables re­quires vec­tor ideas; the bud­ding stat­ist­i­cian and the com­ing phys­i­cist need them; mod­ern ana­lys­is is un­think­able without the no­tion of lin­ear de­pend­ence and all that flows from it. Throughout these courses the in­fu­sion of a geo­met­ric­al point of view is of para­mount im­port­ance. A vec­tor is geo­met­ric­al; it is an ele­ment of a vec­tor space, defined by suit­able ax­ioms — wheth­er the scal­ars be real num­bers or ele­ments of a gen­er­al field. A vec­tor is not an \( n \)-tuple of num­bers un­til a co­ordin­ate sys­tem has been chosen. Any teach­er and any text book which starts with the idea that vec­tors are \( n \)-tuples is com­mit­ting a crime for which the prop­er pun­ish­ment is ri­dicule. The \( n \)-tuple idea is not “easi­er,” it is harder; it is not clear­er, it is more mis­lead­ing. By the same token, lin­ear trans­form­a­tions are ba­sic and matrices are their rep­res­ent­a­tions… ([15], pp. 152–154)

A bib­li­o­graphy of Mac Lane’s works through 1978 is in [19], pp. 545–553. The present bib­li­o­graphy lists works of philo­soph­ic in­terest. Mac Lane’s re­views are lis­ted only when cited above. Mac Lane also made three 60 minute video­tapes for the Amer­ic­an Math­em­at­ic­al So­ci­ety, Provid­ence, Rhode Is­land: “Al­gebra as a means of un­der­stand­ing math­em­at­ics” (a joint AMS-MAA lec­ture, Colum­bus, Ohio, Au­gust 1990), “Fifty years of Math­em­at­ic­al Re­views” (a joint AMS-MAA lec­ture, Louis­ville, Ken­tucky, Janu­ary 1990), “Some ma­jor re­search de­part­ments of math­em­at­ics” (a joint AMS-MAA in­vited ad­dress, Provid­ence, Rhode Is­land, Au­gust 1988).