Celebratio Mathematica

Every planar map of con­nec­ted coun­tries can be colored us­ing four col­ors in such a way that coun­tries with a com­mon bound­ary seg­ment (not just a point) re­ceive dif­fer­ent col­ors. It is amaz­ing that such a simply stated res­ult res­isted proof for one and a quarter cen­tur­ies, and even today it is not yet fully un­der­stood. In this art­icle I con­cen­trate on re­cent de­vel­op­ments: equi­val­ent for­mu­la­tions, a new proof, and pro­gress on some gen­er­al­iz­a­tions.

The Four-Col­or Prob­lem dates back to 1852 when Fran­cis Gu­thrie, while try­ing to col­or the map of the counties of Eng­land, no­ticed that four col­ors suf­ficed. He asked his broth­er Fre­d­er­ick if it was true that any map can be colored us­ing four col­ors in such a way that ad­ja­cent re­gions (i.e., those shar­ing a com­mon bound­ary seg­ment, not just a point) re­ceive dif­fer­ent col­ors. Fre­d­er­ick Gu­thrie then com­mu­nic­ated the con­jec­ture to De­Mor­gan. The first prin­ted ref­er­ence is by Cay­ley in 1878.

A year later the first “proof” by Kempe ap­peared; its in­cor­rect­ness was poin­ted out by Heawood el­ev­en years later. An­oth­er failed proof was pub­lished by Tait in 1880; a gap in the ar­gu­ment was poin­ted out by Petersen in 1891. Both failed proofs did have some value, though. Kempe proved the five-col­or the­or­em (The­or­em 2 be­low) and dis­covered what be­came known as Kempe chains, and Tait found an equi­val­ent for­mu­la­tion of the Four-Col­or The­or­em in terms of edge 3-col­or­ing, stated here as The­or­em 3.

The next ma­jor con­tri­bu­tion came in 1913 from G. D. Birk­hoff, whose work al­lowed Frank­lin to prove in 1922 that the Four-Col­or Con­jec­ture is true for maps with at most 25 re­gions. The same meth­od was used by oth­er math­em­aticians to make pro­gress on the Four-Col­or Prob­lem. Im­port­ant here is the work by Heesch, who de­veloped the two main in­gredi­ents needed for the ul­ti­mate proof — “re­du­cib­il­ity” and “dis­char­ging”. While the concept of re­du­cib­il­ity was stud­ied by oth­er re­search­ers as well, the idea of dis­char­ging, cru­cial for the un­avoid­ab­il­ity part of the proof, is due to Heesch, and he also con­jec­tured that a suit­able de­vel­op­ment of this meth­od would solve the Four-Col­or Prob­lem. This was con­firmed by Ap­pel and Haken (ab­bre­vi­ated A&H) when they pub­lished their proof of the Four-Col­or The­or­em in two 1977 pa­pers, the second one joint with Koch. An ex­pan­ded ver­sion of the proof was later re­prin­ted in [1].

Let me state the res­ult pre­cisely. Rather than try­ing to define maps, coun­tries, and their bound­ar­ies, it is easi­er to re­state Gu­thrie’s 1852 con­jec­ture us­ing planar du­al­ity. For each coun­try we se­lect a cap­it­al (an ar­bit­rary point in­side that coun­try) and join the cap­it­als of every pair of neigh­bor­ing coun­tries. Thus we ar­rive at the no­tion of a plane graph, which is form­ally defined as fol­lows.

A graph \( G \) con­sists of a fi­nite set \( V (G) \), the set of ver­tices of \( G \), a fi­nite set \( E(G) \), the set of edges of \( G \), and an in­cid­ence re­la­tion between ver­tices and edges such that every edge is in­cid­ent with two dis­tinct ver­tices, called its ends. (Thus I per­mit par­al­lel edges, but do not al­low edges that are loops.) A plane graph is a graph \( G \) such that \( V (G) \) is a sub­set of the plane, each edge \( e \) of \( G \) with ends \( u \) and \( v \) is a poly­gon­al arc in the plane with end-points \( u \) and \( v \) and oth­er­wise dis­joint from \( V (G) \), and every two dis­tinct edges are dis­joint ex­cept pos­sibly for their ends. A re­gion of \( G \) is an ar­c­wise-con­nec­ted com­pon­ent of the com­ple­ment of \( G \). A graph is planar if it is iso­morph­ic to a plane graph. (Equi­val­ently, one can re­place “poly­gon­al” in the above defin­i­tion by “con­tinu­ous im­age of \( [0, 1] \)” or, by Fáry’s the­or­em, by “straight line seg­ment”, and the class of planar graphs re­mains the same.) For an in­teger \( k \), a \( k \)-col­or­ing of a graph \( G \) is a map­ping \[ \phi : V (G) \to \{1, \dots, k\} \] such that \( \phi(u) = \phi(v) \) for every edge of \( G \) with ends \( u \) and \( v \). An ex­ample of a plane graph with a 4-col­or­ing is giv­en in the left half of Fig­ure 1 be­low. The Four-Col­or The­or­em (ab­bre­vi­ated 4CT) now can be stated as fol­lows.

While The­or­em 1 presen­ted a ma­jor chal­lenge for sev­er­al gen­er­a­tions of math­em­aticians, the cor­res­pond­ing state­ment for five col­ors is fairly easy to see. Let us state and prove that res­ult now.

Proof.  Let \( G \) be a plane graph, and let \( R \) be the num­ber of re­gions of \( G \). We pro­ceed by in­duc­tion on \( |V (G)| \). We may as­sume that \( G \) is con­nec­ted, has no par­al­lel edges, and has at least three ver­tices. By Euler’s for­mula \[ |V (G)| + R = |E(G)| + 2 .\] Since every edge is in­cid­ent with at most two re­gions and the bound­ary of every re­gion has length at least 3, we have \( 2|E(G)| \geq 3R \). Thus \[ |E(G)| \leq 3|V (G)| - 6 .\] The de­gree of a ver­tex is the num­ber of edges in­cid­ent with it. Since the sum of the de­grees of all ver­tices of a graph equals twice the num­ber of edges, we see that \( G \) has a ver­tex \( v \) of de­gree at most 5.

If \( v \) has de­gree at most 4, we con­sider the graph \( G\backslash v \) ob­tained from \( G \) by de­let­ing \( v \) (and all edges in­cid­ent with \( v \)). The graph \( G\backslash v \) has a 5-col­or­ing by the in­duc­tion hy­po­thes­is, and since \( v \) is ad­ja­cent to at most four ver­tices, this 5-col­or­ing may be ex­ten­ded to a 5-col­or­ing of \( G \). Thus we may as­sume that \( v \) has de­gree 5. I claim that \( J \), the sub­graph of \( G \) in­duced by the neigh­bors of \( v \), has two dis­tinct ver­tices that are not ad­ja­cent to each oth­er. In­deed, oth­er­wise \( J \) has \( \bigl(\begin{smallmatrix}5\\2\end{smallmatrix}\bigr) = 10 \) edges, and yet \[ |E(J)| \leq 3|V (J)| - 6 = 9 \] by the in­equal­ity of the pre­vi­ous para­graph. Thus there ex­ist two dis­tinct neigh­bors \( v_1 \) and \( v_2 \) of \( v \) that are not ad­ja­cent to each oth­er in \( J \), and hence in \( G \). Let \( H \) be the graph ob­tained from \( G\backslash v \) by identi­fy­ing \( v_1 \) and \( v_2 \); it is clear that \( H \) is a graph (it has no loops) and that it may be re­garded as a plane graph. By the in­duc­tion hy­po­thes­is the graph \( H \) has a 5-col­or­ing. This 5-col­or­ing gives rise to a 5-col­or­ing \( \phi \) of \( G\backslash v \) such that \( \phi (v_1 ) = \phi (v_2) \). Thus the neigh­bors of \( v \) are colored us­ing at most four col­ors, and hence \( \phi \) can be ex­ten­ded to a 5-col­or­ing of \( G \), as de­sired. □

For fu­ture ref­er­ence it will be use­ful to sketch an­oth­er proof of The­or­em 2. The ini­tial part pro­ceeds in the same man­ner un­til we reach the one and only non­trivi­al step, namely, when we have a ver­tex \( v \) of de­gree 5 and a 5-col­or­ing \( \phi \) of \( G\backslash v \), giv­ing the neigh­bors of \( v \) dis­tinct col­ors. Let the neigh­bors of \( v \) be \( v_1, v_2, \dots, v_5 \), lis­ted in the or­der in which they ap­pear around \( v \); we may as­sume that \( \phi (v_i ) = i \). Let \( J_{13} \) be the sub­graph of \( G\backslash v \) in­duced by ver­tices \( u \) with \( \phi (u) \in \{1, 3\} \). Let \( \phi^{\prime} \) be the 5-col­or­ing of \( G\backslash v \) ob­tained from \( \phi \) by swap­ping the col­ors 1 and 3 on the com­pon­ent of \( J_{13} \) con­tain­ing \( v_1 \). If \( v_3 \) does not be­long to this com­pon­ent, then \( \phi^{\prime} \) can be ex­ten­ded to a col­or­ing of \( G \) by set­ting \( \phi^{\prime} (v) = 1 \). We may there­fore as­sume that \( v_3 \) be­longs to said com­pon­ent and hence there ex­ists a path \( P_{13} \) in \( G\backslash v \) with ends \( v_1 \) and \( v_3 \) such that \( \phi (u) \in \{1, 3\} \) for every ver­tex \( u \) of \( P_{13} \). Now let \( J_{24} \) be defined ana­log­ously, and by ar­guing in the same man­ner we con­clude that we may as­sume that there ex­ists a path \( P_{24} \) in \( G\backslash v \) with ends \( v_2 \) and \( v_4 \) such that \( \phi(u) \in \{2, 4\} \) for every ver­tex \( u \) of \( P_{24} \). Thus \( P_{13} \) and \( P_{24} \) are ver­tex-dis­joint, con­trary to the Jordan curve the­or­em.

An­oth­er at­tract­ive fea­ture of the 4CT, apart from the sim­pli­city of its for­mu­la­tion, is that it has many equi­val­ent for­mu­la­tions us­ing the lan­guages of sev­er­al dif­fer­ent branches of math­em­at­ics. In­deed, in a 1993 art­icle Kauff­man and Saleur write: “While it has some­times been said that the four-col­or prob­lem is an isol­ated prob­lem in math­em­at­ics, we have found that just the op­pos­ite is the case. The four-col­or prob­lem and the gen­er­al­iz­a­tion dis­cussed here is cent­ral to the in­ter­sec­tion of al­gebra, to­po­logy, and stat­ist­ic­al mech­an­ics.”

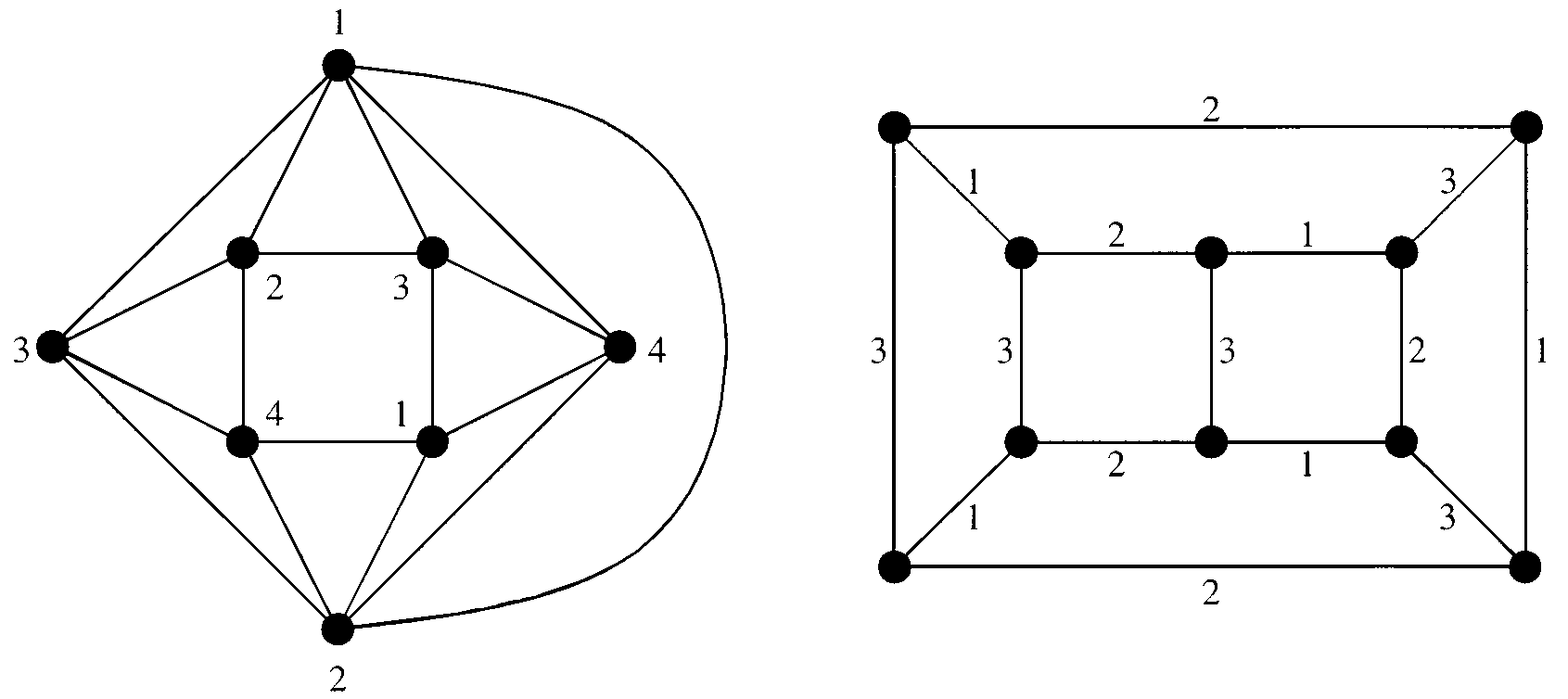
Saaty [e1] presents 29 equi­val­ent for­mu­la­tions of the 4CT. In this art­icle let me re­peat the most clas­sic­al re­for­mu­la­tion and then men­tion three new ones. A graph is cu­bic if every ver­tex has de­gree 3, that is, is in­cid­ent with pre­cisely three edges. An edge 3-col­or­ing of a graph \( G \) is a map­ping \[ \psi : E(G) \to \{1, 2, 3\} \] such that \( \psi (e) \neq \psi (f ) \) for every two edges \( e \) and \( f \) of \( G \) that have a com­mon end. Ex­amples of a cu­bic graph and an edge 3-col­or­ing are giv­en in the right half of Fig­ure 1. A cut-edge of a graph \( G \) is an edge \( e \) such that the graph \( G\backslash e \) ob­tained from \( G \) by de­let­ing \( e \) has more con­nec­ted com­pon­ents than \( G \). It is easy to see that if a cu­bic graph has an edge 3-col­or­ing, then it has no cut-edge. Tait (see also [e2], or [e5]) showed in 1880 that the 4CT is equi­val­ent to the fol­low­ing.

In this art­icle let me re­peat the most clas­sic­al re­for­mu­la­tion and then men­tion three new ones. A graph is cu­bic if every ver­tex has de­gree 3, that is, is in­cid­ent with pre­cisely three edges. An edge 3-col­or­ing of a graph \( G \) is a map­ping \[ \psi : E(G) \to \{1, 2, 3\} \] such that \( \psi (e) =\psi (f ) \) for every two edges \( e \) and \( f \) of \( G \) that have a com­mon end. Ex­amples of a cu­bic graph and an edge 3-col­or­ing are giv­en in the right half of Fig­ure 1. A cut-edge of a graph \( G \) is an edge \( e \) such that the graph \( G\backslash e \) ob­tained from \( G \) by de­let­ing \( e \) has more con­nec­ted com­pon­ents than \( G \). It is easy to see that if a cu­bic graph has an edge 3-col­or­ing, then it has no cut-edge. Tait (see also [e2] or [e5]) showed in 1880 that the 4CT is equi­val­ent to the fol­low­ing.

The equi­val­ence of The­or­ems 1 and 3 is not hard to see and can be found in most texts on graph the­ory. To il­lus­trate where the equi­val­ence comes from, let us see that The­or­em 1 im­plies The­or­em 3. Let \( G \) be a cu­bic plane graph with no cut-edge; we may as­sume that \( G \) is con­nec­ted. The 4CT im­plies that the re­gions of \( G \) can be colored us­ing four col­ors in such a way that the two re­gions in­cid­ent with the same edge re­ceive dif­fer­ent col­ors (those two re­gions are dis­tinct, be­cause \( G \) has no cut-edge). Let us use the col­ors \( (0, 0) \), \( (1, 0) \), \( (0, 1) \), and \( (1, 1) \) in­stead of \( 1, 2, 3, 4 \). Giv­en such a 4-col­or­ing, give an edge of \( G \) the col­or that is the sum of the col­ors of the two re­gions in­cid­ent with it, the sum taken in \( \mathbb{Z}_2\times \mathbb{Z}_2 \). Since the two re­gions in­cid­ent with an edge are dis­tinct, only the col­ors \( (1, 0) \), \( (0, 1) \), and \( (1, 1) \) will be used to col­or the edges of \( G \), giv­ing rise to an edge 3-col­or­ing of \( G \), as de­sired.

Let me now de­scribe three strik­ing re­for­mu­la­tions of the 4CT. The first is sim­il­ar but deep­er than a res­ult found by Whit­ney and dis­cussed in [e1]. Let \( \times \) de­note the vec­tor cross product in \( \mathbb{R}^3 \). The vec­tor cross product is not as­so­ci­at­ive, and hence the ex­pres­sion \[ v_1 \times v_2 \times \cdots \times v_k \] is not well defined, un­less \( k \leq 2 \). In or­der to make the ex­pres­sion well defined, one needs to in­sert par­en­theses to in­dic­ate the or­der of eval­u­ation. By an as­so­ci­ation we mean an ex­pres­sion ob­tained by in­sert­ing \( k - 2 \) pairs of par­en­theses so that the or­der of eval­u­ation is de­term­ined. Thus \[ (v_1 \times v_2 ) \times (v_3 \times v_4 ) \quad \text{and} \quad ((v_1 \times v_2 ) \times v_3 ) \times v_4 \] are two ex­amples of as­so­ci­ations. One can ask wheth­er giv­en two as­so­ci­ations of \[ v_1 \times v_2 \times \cdots \times v_k \] there ex­ists some choice of vec­tors such that the eval­u­ations of the two as­so­ci­ations are equal. This is easy to do by choos­ing \( v_1 = v_2 = \cdots = v_k \). But how about mak­ing the two eval­u­ations equal and nonzero? Kauff­man [e3] has shown the fol­low­ing.

At this point in­ter­ested read­ers might try to prove The­or­em 4 be­fore read­ing fur­ther. After all, it is only a state­ment about the vec­tor cross product in a 3-di­men­sion­al space, and so it can­not be too hard. Or can it? Kauff­man [e3] has also shown:

Let me cla­ri­fy that Kauff­man proves The­or­em 4 by re­du­cing it to the Four-Col­or The­or­em, and so des­pite The­or­em 5 he did not ob­tain a new proof of the 4CT.

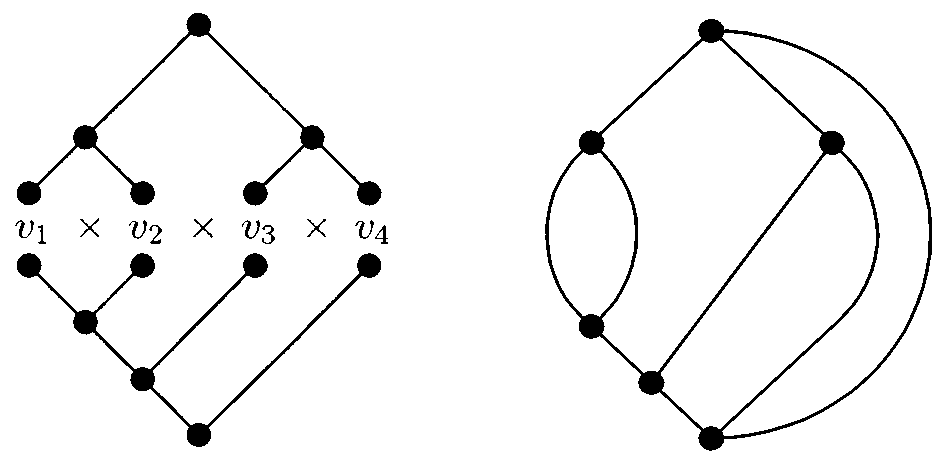
Where does The­or­em 5 come from? To un­der­stand it, we should think of an as­so­ci­ation as a rooted tree in the nat­ur­al sense. Giv­en two as­so­ci­ations \( A_1 \) and \( A_2 \) of \[ v_1 \times v_2 \times \cdots\times v_k ,\] let us grow the cor­res­pond­ing trees \( T_1 \) and \( T_2 \) ver­tic­ally in op­pos­ite dir­ec­tions, as in the left half of Fig­ure 2. Let us join the roots of \( T_1 \) and \( T_2 \) by an edge, identi­fy the leaves cor­res­pond­ing to the same vari­able, and sup­press the res­ult­ing ver­tices of de­gree 2, form­ing a cu­bic plane graph \( H \). This pro­cess is il­lus­trated in the right half of Fig­ure 2. It is easy to see that \( H \) has no cut-edge and hence has an edge 3-col­or­ing by the 4CT. Let us use the col­ors \( \mathbf{i}, \mathbf{j}, \mathbf{k} \) in­stead of 1, 2, 3. No­ti­cing that each vari­able \( v_i \) cor­res­ponds to an edge of \( H \), we see that this edge 3-col­or­ing gives an as­sign­ment of \( \mathbf{i}, \mathbf{j}, \mathbf{k} \) to the vari­ables \( v_1, v_2, \dots, v_k \) and it fol­lows from the con­struc­tion that for this as­sign­ment the ab­so­lute val­ues of the eval­u­ations of \( A_1 \) and \( A_2 \) are equal to the col­or as­signed to the edge of \( H \) that joins the roots of \( T_1 \) and \( T_2 \). Thus we have shown that the 4CT gives an as­sign­ment such that the cor­res­pond­ing eval­u­ations are nonzero and either they are equal or one equals the neg­at­ive of the oth­er. It can in fact be shown that the eval­u­ations are in­deed equal, but we shall not prove that here.

This ex­plains why the 4CT im­plies The­or­em 4. To prove the con­verse, one must show that it suf­fices to prove The­or­em 3 for cu­bic graphs \( H \) that arise in the above man­ner. That fol­lows from a deep the­or­em of Whit­ney on hamilto­ni­an cir­cuits in planar tri­an­gu­la­tions.

For the next re­for­mu­la­tion let \( L \) de­note the Lie al­gebra \( \operatorname{sl}(N) \), that is, the vec­tor space of all real \( N \times N \) matrices with trace zero and with the product \( [A, B] \) defined by \[ [A, B] = AB - BA .\] Let \( \{A_i\} \) be a vec­tor space basis of \( L \). The met­ric tensor \( t_{ij} \) is defined by \( t_{ij} = \operatorname{tr} (A_i, A_j) \), where \( \operatorname{tr} \) de­notes the trace of a mat­rix. Let \( t^{ij} \) de­note the in­verse of the met­ric tensor, and let \( f_{ijk} \) be the struc­ture con­stants of \( L \), defined by \[ f_{ijk} = \operatorname{tr} (A_i [A_j, A_k ]) .\] Now let \( G \) be a cu­bic graph, and let us choose, for every ver­tex \( v \in V (G) \), a cyc­lic per­muta­tion of the edges of \( G \) in­cid­ent with \( v \). Our ob­ject­ive is to define an in­vari­ant \( W_L (G) \). To this end, let us break every edge of \( G \) in­to two half-edges and la­bel all the half-edges by in­dices from \( \{1, 2, \dots \), \( \dim L\} \). With each such la­beling \( \lambda \) we as­so­ci­ate the product \[ \pi(\lambda) = \prod_{v\in V(G)} fv \prod_{e\in E(G)}t^e, \] where \( t^e = t^{ij} \) if the two half-edges of \( e \) have la­bels \( i \) and \( j \) (no­tice that \( t^{ij} = t^{ji} \)) and \( f_v = f_{ijk} \) if the three half-edges in­cid­ent with \( v \) have la­bels \( i, j, k \) and oc­cur around \( v \) in the cyc­lic or­der lis­ted (no­tice that \( f_{ijk} = f_{jki} = f_{kij} \)). Fi­nally, we define \( W_L (G) \) as the ab­so­lute value of the sum of \( \pi (\lambda) \) taken over all la­belings \( \lambda \) of the half-edges of \( G \) by ele­ments of \( \{1, 2, \dots \), \( \dim L\} \). It fol­lows that \( W_L (G) \) does not de­pend on the choice of the cyc­lic per­muta­tions. It can also be shown that \( W_L (G) \) does not de­pend on the choice of basis, but for our pur­poses it suf­fices to stick to one fixed basis. Fur­ther, it can be shown that \( W_L (G) \) is a poly­no­mi­al in \( N \) of de­gree at most \( k = \frac{1}{2} |V (G)| + 2 \), and so we can define \( W^{\operatorname{top}}_L (G) \) to be the coef­fi­cient of \( N^k \) in \( W_L(G) \). The next res­ult, due to Bar-Natan [e8], is best in­tro­duced by a quote from his pa­per: “For us who grew up think­ing that all there is to learn about \( \operatorname{sl}(N) \) is already in \( \operatorname{sl}(2) \), this is not a big sur­prise.”

However, the fol­low­ing the­or­em of Bar-Natan is sur­pris­ing, re­gard­less of what one grew up think­ing about the re­la­tion­ship of \( \operatorname{sl}(2) \) and \( \operatorname{sl}(N) \).

Like The­or­em 4, The­or­em 6 is de­duced from the Four-Col­or The­or­em, and hence The­or­em 7 does not yield a new proof of the 4CT.

There is an easy hint as to why The­or­em 7 holds. Pen­rose has shown that \( W_{\operatorname{sl}(2)} (G) \) is a nonzero con­stant mul­tiple of the num­ber of edge 3-col­or­ings of \( G \). Bar-Natan has shown that if \( G \) is a con­nec­ted cu­bic graph, then \( W^{\operatorname{top}}_{\operatorname{sl}(N)} (G) \) is 0 if \( G \) has a cut-edge and is equal to the num­ber of em­bed­dings of \( G \) in the sphere oth­er­wise. The two res­ults com­bined with The­or­em 3 im­me­di­ately es­tab­lish The­or­ems 6 and 7. The de­tails may be found in [e8].

The last re­for­mu­la­tion, in terms of di­vis­ib­il­ity, is due to Matiy­a­sevich [e9].

In fact, Matiy­a­sevich found the func­tions \( A_k \), \( B_k \), \( C_k \), and \( D_k \) ex­pli­citly, and he con­jec­tures that a more gen­er­al state­ment holds.

Let us try to un­der­stand where this the­or­em comes from. Let \( \mathbb{N} \) de­note the set of non­neg­at­ive in­tegers. For a pos­it­ive in­teger \( n \) let \( S_n \) de­note the in­fin­ite graph with ver­tex-set \( \mathbb{N} \) in which ver­tices \( i \) and \( j \) are ad­ja­cent if \( |i - j| = 1 \) or \( |i - j| = n \). A dis­crete map is a pair \( (n, \mu) \), where \( n \in \mathbb{N} \) and \( \mu : \mathbb{N} \to \mathbb{N} \) is a map­ping such that \( \mu(i) = 0 \) for all but fi­nitely many \( i \in \mathbb{N} \). A dis­crete map \( (n, \mu) \) gives rise to a graph as fol­lows. Let \( H^{\prime} \) be the sub­graph of \( S_n \) in­duced by all ver­tices \( i \) with \( \mu(i) \neq 0 \), and let \( H \) be ob­tained from \( H^{\prime} \) by con­tract­ing all edges with ends \( i, j , \) where \( \mu(i) = \mu (j) \). Then \( H \) is in­deed a graph (it is loop­less), and \( \mu \) is a col­or­ing of \( H \). We say that two dis­crete maps \( (n, \mu) \) and \( (n^{\prime}, \mu^{\prime}) \) are equi­val­ent if

• \( n = n^{\prime} \),
• \( \mu(i) = 0 \) if and only if \( \mu^{\prime}(i) = 0 \),
• \( \mu (i) = \mu (i + 1) \) if and only if \( \mu^{\prime}(i) = \mu^{\prime}(i + 1) \), and
• \( \mu (i) = \mu(i + n) \) if and only if \( \mu^{\prime} (i) = \mu^{\prime} (i + n) \).

It is not too dif­fi­cult to show that every planar graph arises as the planar graph \( H \) above for some dis­crete map and hence the 4CT is equi­val­ent to

By The­or­em 2 we can in the above the­or­em con­fine ourselves to dis­crete maps \( (n, \mu) \) such that \( \mu (i) \in \{0, 1, 2, 3, 4,5\} \) for all \( i \in \mathbb{N} \). Each such func­tion \( \mu \) can be en­coded as an in­teger \[ m =\sum^{\infty}_{i=0} \mu (i)7^i .\] Thus the phrase “for every two in­tegers \( n, m \)” in The­or­em 8 plays the role of “for every plane graph”. Sim­il­arly, the func­tion \( \lambda \) can be en­coded as an in­teger, but we prefer to en­code it us­ing the 20 in­tegers \( c_1, c_2, \dots, c_{20} \) defined for \( i = 0, 1, \dots, 4 \) and \( j = 1, 2, 3, 4 \) by \[ c_{4i+j} =\sum (7^k : \mu(k) = i + 1, \lambda(k) = j). \] Now there are con­di­tions the in­tegers \( c_1, c_2,\dots, c_{20} \) have to sat­is­fy in or­der to rep­res­ent a val­id dis­crete map \( (n, \lambda) \) as in The­or­em 9, but each such con­di­tion can be ex­pressed in the form “7 does not di­vide \( \bigl(\begin{smallmatrix} A+7^nB\\C+7^n D\end{smallmatrix}\bigr) \)”, where \( A, B, C, D \) are lin­ear func­tions of \( m, c_1, c_2, \dots, c_{20} \). The read­er may find more de­tails in [e9].

The work of Ap­pel and Haken un­doubtedly rep­res­ents a ma­jor break­through in math­em­at­ics, but, un­for­tu­nately, there re­mains some skep­ti­cism re­gard­ing the valid­ity of their proof. To il­lus­trate the nature of those con­cerns, let me quote from a 1986 art­icle by Ap­pel and Haken them­selves: “This leaves the read­er to face 50 pages con­tain­ing text and dia­grams, 85 pages filled with al­most 2500 ad­di­tion­al dia­grams, and 400 mi­crofiche pages that con­tain fur­ther dia­grams and thou­sands of in­di­vidu­al veri­fic­a­tions of claims made in the 24 lem­mas in the main sec­tions of text. In ad­di­tion, the read­er is told that cer­tain facts have been veri­fied with the use of about 1200 hours of com­puter time and would be ex­tremely time-con­sum­ing to veri­fy by hand. The pa­pers are some­what in­tim­id­at­ing due to their style and length and few math­em­aticians have read them in any de­tail.”

A dis­cus­sion of er­rors, their cor­rec­tion, and oth­er po­ten­tial prob­lems may be found in the above art­icle, in [1], and in F. Bernhart’s re­view of [1]. For the pur­pose of this sur­vey, let me tele­scope the dif­fi­culties with the A&H proof in­to two points:

1. part of the proof uses a com­puter and can­not be veri­fied by hand, and
2. even the part that is sup­posedly hand-check­able has not, as far as I know, been in­de­pend­ently veri­fied in its en­tirety.

To my know­ledge, the most com­pre­hens­ive ef­fort to veri­fy the A&H proof was un­der­taken by Schmidt. Ac­cord­ing to [1], dur­ing the one-year lim­it­a­tion im­posed on his mas­ter’s thes­is Schmidt was able to veri­fy about 40 per­cent of part I of the A&H proof.

Neil Robertson, Daniel P. Sanders, Paul Sey­mour, and I tried to veri­fy the Ap­pel–Haken proof, but soon gave up and de­cided that it would be more prof­it­able to work out our own proof. So we did and came up with the proof that is out­lined be­low. We were not able to elim­in­ate reas­on (1), but we man­aged to make pro­gress to­ward (2).

The ba­sic idea of our proof is the same as Ap­pel and Haken’s. We ex­hib­it a set of 633 “con­fig­ur­a­tions” and prove each of them is “re­du­cible”. This is a tech­nic­al concept that im­plies that no con­fig­ur­a­tion with this prop­erty can “ap­pear” in a min­im­al counter­example to the Four-Col­or The­or­em. It can also be used in an al­gorithm, for if a re­du­cible con­fig­ur­a­tion ap­pears in a suf­fi­ciently con­nec­ted planar graph \( G \), then one can con­struct in con­stant time a smal­ler planar graph \( G^{\prime} \) such that any 4-col­or­ing of \( G^{\prime} \) can be con­ver­ted to a 4-col­or­ing of \( G \) in lin­ear time.

Birk­hoff showed in 1913 that every min­im­al counter­example to the Four-Col­or The­or­em is an “in­tern­ally 6-con­nec­ted” tri­an­gu­la­tion. In the second part of the proof we prove that at least one of our 633 con­fig­ur­a­tions ap­pears in every in­tern­ally 6-con­nec­ted planar tri­an­gu­la­tion (not ne­ces­sar­ily a min­im­al counter­example to the 4CT). This is called prov­ing un­avoid­ab­il­ity and uses the “dis­char­ging meth­od” first sug­ges­ted by Heesch. Here our meth­od dif­fers from that of Ap­pel and Haken.

The main as­pects of our proof are as fol­lows. We con­firm a con­jec­ture of Heesch that in prov­ing un­avoid­ab­il­ity a re­du­cible con­fig­ur­a­tion can be found in the second neigh­bor­hood of an “over-charged” ver­tex; this is how we avoid “im­mer­sion” prob­lems that were a ma­jor source of com­plic­a­tion for Ap­pel and Haken. Our un­avoid­able set has size 633 as op­posed to the 1,476-mem­ber set of Ap­pel and Haken; our dis­char­ging meth­od uses only 32 dis­char­ging rules in­stead of the 487 of Ap­pel and Haken; and we ob­tain a quad­rat­ic al­gorithm to 4-col­or planar graphs, an im­prove­ment over the quart­ic al­gorithm of Ap­pel and Haken. Our proof, in­clud­ing the com­puter part, has been in­de­pend­ently veri­fied, and the ideas have been and are be­ing used to prove more gen­er­al res­ults. Fi­nally, the main steps of our proof are easi­er to present, as I will at­tempt to demon­strate be­low.

Be­fore I turn to a more de­tailed dis­cus­sion of con­fig­ur­a­tions, re­du­cib­il­ity, and dis­char­ging, let me say a few words about the use of com­puters in our proof. The the­or­et­ic­al part is com­pletely de­scribed in [e6], but it re­lies on two res­ults that are stated as hav­ing been proven by a com­puter. The rest of [e6] con­sists of tra­di­tion­al (com­puter-free) math­em­at­ic­al ar­gu­ments. There is noth­ing ex­traordin­ary about the the­or­et­ic­al ar­gu­ments, and so the main bur­den of veri­fic­a­tion lies in those two com­puter proofs. How is one sup­posed to be con­vinced of their valid­ity? There are ba­sic­ally two ways. The read­er can either write his or her own com­puter pro­grams to check those res­ults (they are eas­ily seen to be fi­nite prob­lems), or he or she can down­load our pro­grams along with their sup­port­ing doc­u­ment­a­tion and veri­fy that those pro­grams do what we claim they do.

The re­du­cib­il­ity part is easi­er to be­lieve, be­cause we are do­ing al­most the same thing as many au­thors be­fore us (in­clud­ing Ap­pel and Haken) have done, and so it is pos­sible to com­pare cer­tain nu­mer­ic­al in­vari­ants ob­tained dur­ing the com­pu­ta­tion to gain faith in the res­ults. This is not pos­sible in the un­avoid­ab­il­ity part, be­cause our ap­proach to it is new. To fa­cil­it­ate check­ing, we have writ­ten this part of the com­puter proof in a form­al lan­guage so that it will be ma­chine veri­fi­able. Every line of the proof can be read and checked by a hu­man, and so can (at least the­or­et­ic­ally) the whole ar­gu­ment. However, the en­tire ar­gu­ment oc­cu­pies about 13,000 lines, and each line takes some thought to veri­fy. There­fore, veri­fy­ing all of this without a com­puter would re­quire an amount of per­sist­ence and de­term­in­a­tion my coau­thors and I do not pos­sess. The com­puter data, pro­grams, and doc­u­ment­a­tion are avail­able by an­onym­ous ftp1 and can also be con­veni­ently ac­cessed on the World Wide Web.2

Two of my stu­dents in­de­pend­ently veri­fied the com­puter work. Tom Fowl­er veri­fied the re­du­cib­il­ity part (and in fact ex­ten­ded it to ob­tain a more gen­er­al res­ult — see later), and Chris­toph­er Carl Heck­man wrote an in­de­pend­ent ver­sion of the un­avoid­ab­il­ity part us­ing a dif­fer­ent pro­gram­ming lan­guage. Bojan Mo­har also in­formed us that his stu­dent Gašper Fijavž wrote in­de­pend­ent pro­grams and was able to con­firm both parts of the com­puter proof. The com­puter veri­fic­a­tion can be car­ried out in a mat­ter of sev­er­al hours on stand­ard com­mer­cially avail­able equip­ment.

I should men­tion that both our pro­grams use only in­teger arith­met­ic, and so we need not be con­cerned with round-off er­rors and sim­il­ar dangers of float­ing point arith­met­ic. However, an ar­gu­ment can be made that our “proof” is not a proof in the tra­di­tion­al sense, be­cause it con­tains steps that most likely can nev­er be veri­fied by hu­mans. In par­tic­u­lar, we have not proven the cor­rect­ness of the com­piler on which we com­piled our pro­grams, nor have we proven the in­fal­lib­il­ity of the hard­ware on which we ran our pro­grams. These have to be taken on faith and are con­ceiv­ably a source of er­ror. However, from a prac­tic­al point of view, the chance of a com­puter er­ror that ap­pears con­sist­ently in ex­actly the same way on all runs of our pro­grams on all the com­pilers un­der all the op­er­at­ing sys­tems that our pro­grams run on is in­fin­ites­im­ally small com­pared to the like­li­hood of a hu­man er­ror dur­ing the same amount of case-check­ing. Apart from this hy­po­thet­ic­al pos­sib­il­ity of a com­puter con­sist­ently giv­ing an in­cor­rect an­swer, the rest of our proof, in­clud­ing the pro­grams, can be checked in the same way as tra­di­tion­al math­em­at­ic­al proofs. My coau­thors and I con­cede, however, that check­ing a com­puter pro­gram is much more dif­fi­cult than veri­fy­ing a math­em­at­ic­al proof of the same length.

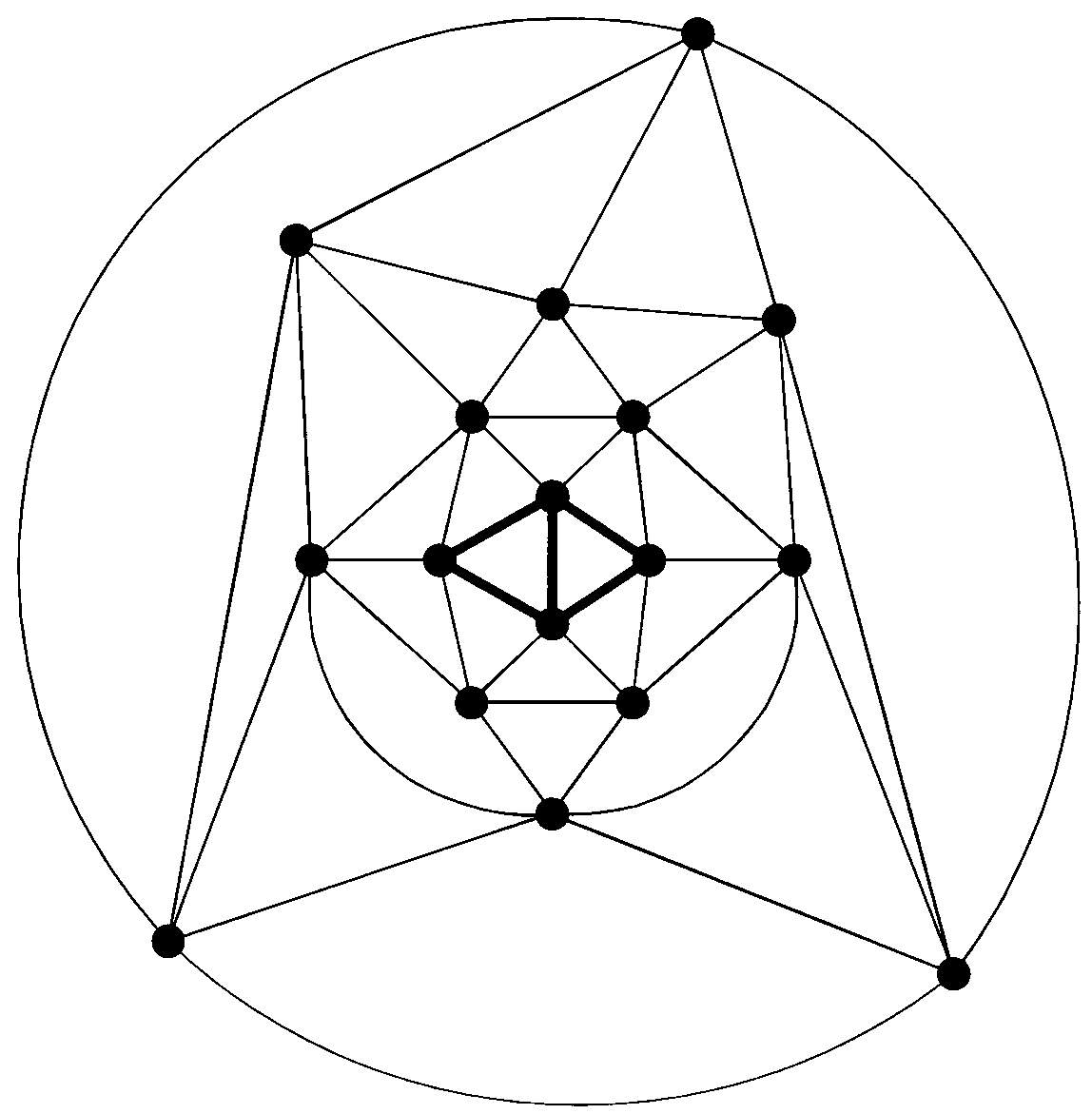
First we need a res­ult of Birk­hoff about con­nectiv­ity of min­im­al counter­examples. Let \( G \) be a plane graph. A tri­angle is a re­gion of \( G \) bounded by pre­cisely three edges of \( G \). A plane graph \( G \) is a tri­an­gu­la­tion if every re­gion of \( G \) (in­clud­ing the un­boun­ded re­gion) is a tri­angle. See Fig­ure 3 for an ex­ample. A graph \( G \) is in­tern­ally 6-con­nec­ted if for every set \( X \) of at most five ver­tices, either the graph \( G\backslash X \) ob­tained from \( G \) by de­let­ing \( X \) is con­nec­ted, or \( |X| = 5 \) and \( G\backslash X \) has ex­actly two con­nec­ted com­pon­ents, one of which con­sists of a single ver­tex. Thus every ver­tex of an in­tern­ally 6-con­nec­ted graph has de­gree at least 5. For ex­ample, the tri­an­gu­la­tion in Fig­ure 3 is in­tern­ally 6-con­nec­ted. Let me form­ally state the res­ult of Birk­hoff men­tioned earli­er. A proof can be ob­tained by push­ing the ar­gu­ments presen­ted in the two proofs of The­or­em 2.

Next we need to in­tro­duce the concept of a con­fig­ur­a­tion, which is cent­ral to the rest of the proof. Con­fig­ur­a­tions are tech­nic­al devices that per­mit us to cap­ture the struc­ture of a small part of a lar­ger tri­an­gu­la­tion. A graph \( G \) is an in­duced sub­graph of a graph \( T \) if \( G \) is a sub­graph of \( T \) and every edge of \( T \) with both ends in \( V (G) \) be­longs to \( G \). If \( (G, \gamma) \) is a con­fig­ur­a­tion, one should think of \( G \) as an in­duced sub­graph of an in­tern­ally 6-con­nec­ted tri­an­gu­la­tion \( T \), with \( \gamma(v) \) be­ing the de­gree of \( v \) in \( T \). This no­tion can be traced back to Birk­hoff’s 1913 pa­per and has been used in vari­ous forms by many re­search­ers since then. Here is the form­al defin­i­tion of the ver­sion that we use.

A near-tri­an­gu­la­tion is a non­null con­nec­ted plane graph with one re­gion des­ig­nated as spe­cial such that every re­gion, ex­cept pos­sibly the spe­cial re­gion, is a tri­angle. A con­fig­ur­a­tion \( K \) is a pair \( (G, \gamma) \), where \( G \) is a near-tri­an­gu­la­tion and \( \gamma \) is a map­ping from \( V(G) \) to the in­tegers with the fol­low­ing prop­er­ties:

1. for every ver­tex \( v \) of \( G \), if \( v \) is not in­cid­ent with the spe­cial re­gion of \( G \), then \( \gamma(v) \) equals \( \deg(v) \), the de­gree of \( v \), and oth­er­wise \( \gamma(v) > \deg(v) \), and in either case \( \gamma(v) \geq 5 \);
2. for every ver­tex \( v \) of \( G \), \( G\backslash v \) has at most two com­pon­ents, and if there are two, then the de­gree of \( v \) in \( G \) is \( \gamma (v) - 2 \);
3. \( K \) has ring-size at least 2, where the ring-size of \( K \) is defined to be \[ \sum(\gamma(v) - \deg(v) - 1) ,\] summed over all ver­tices \( v \) in­cid­ent with the spe­cial re­gion of \( G \) such that \( G\backslash v \) is con­nec­ted.

The sig­ni­fic­ance of con­di­tion (1) will be­come clear­er from the defin­i­tion of “ap­pears” be­low; con­di­tions (2) and (3) are needed for the defin­i­tion of the “free com­ple­tion”, dis­cussed in the next sec­tion.

When draw­ing pic­tures of con­fig­ur­a­tions, one pos­sib­il­ity is to draw the un­der­ly­ing graph and write the value of \( \gamma \) next to each ver­tex. There is a more con­veni­ent way, in­tro­duced by Heesch. The spe­cial re­gion is the un­boun­ded re­gion, and the shapes of ver­tices in­dic­ate the value of \( \gamma(v) \) as fol­lows: A sol­id black circle means \( \gamma(v) = 5 \), a dot (or what ap­pears in the pic­ture as no sym­bol at all) means \( \gamma(v) = 6 \), a hol­low circle means \( \gamma(v) = 7 \), a hol­low square means \( \gamma(v) = 8 \), a tri­angle means \( \gamma(v) = 9 \), and a pentagon means \( \gamma(v) = 10 \). In Fig­ure 4, 17 of our 633 re­du­cible con­fig­ur­a­tions are dis­played us­ing the in­dic­ated con­ven­tion. The whole set can be found in [e6] and can be viewed elec­tron­ic­ally.3

Iso­morph­ism of con­fig­ur­a­tions is defined in the nat­ur­al way. Any con­fig­ur­a­tion iso­morph­ic to one of the 633 con­fig­ur­a­tions ex­hib­ited in [e6] is called a good con­fig­ur­a­tion. Let \( T \) be a tri­an­gu­la­tion. A con­fig­ur­a­tion \( (G, \gamma) \) ap­pears in \( T \) if \( G \) is an in­duced sub­graph of \( T \), every re­gion of \( G \) ex­cept pos­sibly the spe­cial re­gion is a re­gion of \( T \), and \( \gamma(v) \) equals the de­gree of \( v \) in \( T \) for every ver­tex \( v \) of \( G \). See Fig­ure 3 for an ex­ample of a con­fig­ur­a­tion iso­morph­ic to the first con­fig­ur­a­tion in Fig­ure 4 ap­pear­ing in an in­tern­ally 6-con­nec­ted tri­an­gu­la­tion. We prove the fol­low­ing two state­ments.

For ex­ample, the good con­fig­ur­a­tion in the up­per left corner of Fig­ure 4 ap­pears in the cen­ter of Fig­ure 3.

From The­or­ems 10, 11, and 12 it fol­lows that no min­im­al counter­example ex­ists, and so the 4CT is true. I will dis­cuss the proofs of the lat­ter two the­or­ems in the next two sec­tions.

Re­du­cib­il­ity is a tech­nique for prov­ing state­ments such as The­or­em 11. Qual­it­at­ively it can be de­scribed by say­ing that it is ob­tained by push­ing to the lim­it the ar­gu­ments used in the two proofs of The­or­em 2. It was de­veloped from Kempe’s failed at­tempt at prov­ing the 4CT by Birk­hoff, Bernhart, Heesch, Al­laire, Swart, Ap­pel and Haken, and oth­ers.

I will ex­plain the idea of re­du­cib­il­ity by giv­ing an ex­ample; in­ter­ested read­ers may find the pre­cise defin­i­tion in [e6]. Let us con­sider the first con­fig­ur­a­tion in Fig­ure 4, and let us call it \( K = (G, \gamma) \). Sup­pose for a con­tra­dic­tion that \( K \) ap­pears in a min­im­al counter­example \( T \) to the 4CT. Giv­en that \( \gamma(v) \) is equal to the de­gree in \( T \) of the ver­tex \( v \) of \( G \), we can de­duce what \( T \) looks like in a small “neigh­bor­hood” of \( G \). In fact, since \( T \) is in­tern­ally 6-con­nec­ted by The­or­em 10, it fol­lows that the graph \( S \) pic­tured in Fig­ure 5 is iso­morph­ic to a sub­graph of \( T \), and so we may as­sume that \( S \) is ac­tu­ally a sub­graph of \( T \). No­tice that \( G \) is a sub­graph of \( S \), that \( R = S\backslash V (G) \) is a (simple) cir­cuit with ver­tex-set \( \{v_1, v_2, \dots \), \( v_6\} \), and that the length of \( R \) is equal to the ring-size of \( K \). We call \( S \) the free com­ple­tion of \( K \).

(Here we were lucky — for lar­ger con­fig­ur­a­tions it does not fol­low that the free com­ple­tion is a sub­graph of \( T \). However, the most that can hap­pen, giv­en that \( G \) is an in­duced sub­graph of \( T \), is that for some dis­tinct ver­tices of \( R \) the cor­res­pond­ing ver­tices of \( T \) are equal. On the oth­er hand, this does not mat­ter for the forth­com­ing ar­gu­ment, and so for the pur­pose of this art­icle let me ig­nore this pos­sib­il­ity.)

Now let us con­sider \[ T^{\prime} = T \backslash V (G) .\] Let \( \mathcal{K} \) be the set of all 4-col­or­ings of \( R \), and let \( \mathcal{C}^{\prime}\subseteq \mathcal{K} \) be the set of all those 4-col­or­ings of \( R \) that ex­tend to a 4-col­or­ing of \( T^{\prime} \). Since \( T \) is a min­im­al counter­example, \( T^{\prime} \) has a 4-col­or­ing, and hence \( \mathcal{C}^{\prime} = \emptyset \). To ob­tain a con­tra­dic­tion, let me prove that \( \mathcal{C}^{\prime} = \emptyset \). Let \( \mathcal{C} \) be the set of all 4-col­or­ings of \( R \) that ex­tend to a 4-col­or­ing of \( S \). No­tice that \( \mathcal{C} \) can be com­puted from the know­ledge of the con­fig­ur­a­tion \( K \). Since \( T \) is a counter­example to the 4CT, \( \mathcal{C}^{\prime} \subseteq \mathcal{K} - \mathcal{C} \) (oth­er­wise a 4 -col­or­ing of \( R \) that ex­tends to both \( S \) and \( T^{\prime} \) ex­tends to a 4-col­or­ing of \( T \)). We need a meth­od that would al­low us to show that a 4-col­or­ing \( \phi \in \mathcal{K} - \mathcal{C} \) does not be­long to \( \mathcal{C}^{\prime} \). As an ex­ample let us con­sider the 4-col­or­ing \( \phi \) of \( R \) defined by \[ (\phi(v_1 ), \phi(v_2 ), \dots, \phi(v_6)) = (1, 2, 1, 3, 1, 2) ,\] where \( v_1, v_2, \dots, v_6 \) are the ver­tices of \( R \), numbered as in Fig­ure 5. To sim­pli­fy the nota­tion, I shall write \( \phi = 121312 \) and sim­il­arly for oth­er col­or­ings. Sup­pose for a con­tra­dic­tion that \( \phi \in \mathcal{C}^{\prime} \), and let \( \kappa \) be a 4-col­or­ing of \( T^{\prime} \) ex­tend­ing \( \phi \). Let \( T_{14} \) be the sub­graph of \( T^{\prime} \) in­duced by the ver­tices \( v \in V (T^{\prime}) \) with \( \kappa(v) \in \{1, 4\} \), and let \( L \) be the com­pon­ent of \( T_{14} \) con­tain­ing the ver­tex \( v_1 \). Let \( \kappa^{\prime} \) be ob­tained from \( \kappa \) by ex­chan­ging col­ors 1 and 4 on ver­tices of \( L \), and let \( \phi^{\prime} \) be the re­stric­tion of \( \kappa^{\prime} \) to \( R \). Thus \( \phi^{\prime} \in \mathcal{C}^{\prime} \). If \( v_3 , v_5 \notin V (L) \), then \( \phi^{\prime} = 421312 \), and if \( v_3 \notin V (L) \), \( v_5 \in V (L) \), then \( \phi^{\prime} = 421342 \). In either case \( \phi^{\prime} \in \mathcal{C} \) (see Fig­ure 6), a con­tra­dic­tion. Thus \( v_3 \in V (L) \), and hence there ex­ists a path \( P \) in \( T^{\prime} \) with ends \( v_1 \) and \( v_3 \) such that \( \kappa(v) \in \{1, 4\} \) for every \( v \in V (P ) \). Let \( T_{23} \) be defined ana­log­ously, and let \( J \) be the com­pon­ent of \( T_{23} \) con­tain­ing \( v_2 \). Since \( V (J) \cup V (P ) = \emptyset \) we de­duce from the Jordan curve the­or­em that \( v_4, v_6 \notin V (J) \). Let \( \kappa^{\prime\prime} \) be ob­tained from \( \kappa \) by ex­chan­ging col­ors 2 and 3 on ver­tices of \( J \), and let \( \phi^{\prime\prime} \) be the re­stric­tion of \( \kappa^{\prime\prime} \) to \( R \). Then \( \phi^{\prime\prime} = 131312 \), and hence \( \phi^{\prime\prime} \in \mathcal{C} \) (see Fig­ure 6), and yet \( \phi^{\prime\prime} \in \mathcal{C}^{\prime} \), a con­tra­dic­tion. Thus \( \phi \notin \mathcal{C}^{\prime} \), as re­quired. The ar­gu­ments for oth­er col­or­ings in \( \mathcal{K} - \mathcal{C} \) pro­ceed sim­il­arly. The or­der in which col­or­ings are handled is im­port­ant here, be­cause for some col­or­ings it is ne­ces­sary to use the pre­vi­ously es­tab­lished fact that oth­er col­or­ings in \( \mathcal{K} - \mathcal{C} \) do not be­long to \( \mathcal{C}^{\prime} \).

The above ar­gu­ment is called D-re­du­cib­il­ity in the lit­er­at­ure. No­tice the way in which we used the fact that \( T \) is a min­im­al counter­example — we used it to de­duce that \( T^{\prime} \) has a 4-col­or­ing. This may seem waste­ful, for rather than de­let­ing \( G \), we could re­place it by a smal­ler graph \( G^{\prime} \). Do­ing so yields a more power­ful meth­od, called C-re­du­cib­il­ity. In our proof of the 4CT we use a spe­cial case of C-re­du­cib­il­ity, where \( G^{\prime} \) is ob­tained from \( G \) by con­tract­ing at most four edges. C-re­du­cib­il­ity is dan­ger­ous in gen­er­al, be­cause it re­quires check­ing that the new graph ob­tained by sub­sti­tut­ing \( G^{\prime} \) for \( G \) is loop­less, which can be rather te­di­ous. By lim­it­ing ourselves to graphs ob­tained by con­tract­ing at most four edges, we were able to elim­in­ate these dif­fi­culties.

D- and C-re­du­cib­il­ity can be auto­mated and car­ried out on a com­puter. In fact, they must be car­ried out on a com­puter, be­cause we need to test con­fig­ur­a­tions with ring-size as large as 14, in which case there are al­most 200,000 col­or­ings to be checked. At the present time there is little hope of do­ing this part of the proof by hand. Even writ­ing down the proof in a form­al lan­guage, as we did for the dis­char­ging part, does not seem prac­tic­al be­cause of the length of the ar­gu­ment.

Dis­char­ging is a clev­er and ef­fect­ive use of Euler’s for­mula, first sug­ges­ted by Heesch and later used by Ap­pel and Haken and many oth­ers since then. In fact, dis­char­ging has be­come a stand­ard tool in graph the­ory. In what fol­lows I will refer to Fig­ure 7, which some read­ers may find over­whelm­ing at the first sight. I re­com­mend fo­cus­ing at­ten­tion on the first row and think­ing of the rest as be­ing of sec­ond­ary im­port­ance. The first row has a geo­met­ric in­ter­pret­a­tion, dis­cussed be­low. Also, we will make use of Heesch’s nota­tion­al con­ven­tion in­tro­duced two para­graphs pri­or to The­or­em 11.

Let \( T \) be an in­tern­ally 6-con­nec­ted tri­an­gu­la­tion. Ini­tially, every ver­tex \( v \) is as­signed a charge of \[ 10(6 - \deg(v)) .\] It fol­lows from Euler’s for­mula that the sum of the charges of all ver­tices is 120; in par­tic­u­lar, it is pos­it­ive. We now re­dis­trib­ute the charges ac­cord­ing to the fol­low­ing rules. Whenev­er \( T \) has a sub­graph iso­morph­ic to one of the graphs in Fig­ure 7 sat­is­fy­ing the de­gree spe­cific­a­tions (for a ver­tex \( v \) of one of those graphs with a minus sign next to \( v \), this means that the de­gree of the cor­res­pond­ing ver­tex of \( T \) is at most the value spe­cified by the shape of \( v \), and ana­log­ously for ver­tices with a plus sign next to them; equal­ity is re­quired for ver­tices with no sign next to them), a charge of 1 (2 in case of the first graph) is to be sent along the edge marked with an ar­row.

This pro­ced­ure defines a new set of charges with the same total sum. For in­stance, if \( T \) is the tri­an­gu­la­tion de­pic­ted in Fig­ure 3, then only the rule cor­res­pond­ing to the first graph in Fig­ure 7 ap­plies, and it causes a charge of 2 to be sent along each edge in either dir­ec­tion. Hence the net ef­fect of all the rules is zero, and so every ver­tex ends up with a fi­nal charge of 10.

Since the total sum of the new charges is pos­it­ive, there is a ver­tex \( v \) in \( T \) whose new charge is pos­it­ive. We show that a good con­fig­ur­a­tion ap­pears in the second neigh­bor­hood of \( v \) (that is, the sub­graph in­duced by ver­tices at dis­tance at most 2 from \( v \)). If the de­gree of \( v \) is at most 6 or at least 12, then this can be seen fairly eas­ily by a dir­ect ar­gu­ment. (See [e6] for de­tails; for this ar­gu­ment the con­fig­ur­a­tions of Fig­ure 4 suf­fice. In fact, when \( v \) has de­gree at most 6, this fol­lows im­me­di­ately from the geo­met­ric in­ter­pret­a­tion of the first row of Fig­ure 7 giv­en at the end of this sec­tion.) For the re­main­ing cases, however, the proofs are much more com­plic­ated. Since the amount of charge a ver­tex of \( T \) re­ceives de­pends only on its second neigh­bor­hood (and not on the rest of \( T \)), it suf­fices to ex­am­ine all pos­sible second neigh­bor­hoods of ver­tices of de­gree 7, 8, 9, 10, and 11. It is easy to see that this re­duces to a fi­nite prob­lem. Strictly speak­ing, there are in­fin­itely many such second neigh­bor­hoods, but for ver­tices of de­gree at least 12 the ac­tu­al de­gree af­fects neither the amount of charge nor the pres­ence of re­du­cible con­fig­ur­a­tions. Thus all pos­sible second neigh­bor­hoods can be di­vided in­to fi­nitely many classes, where for every two second neigh­bor­hoods in the same class, the same good con­fig­ur­a­tions ap­pear and the cent­ral ver­tex has the same charge. There­fore, it suf­fices to ex­am­ine all these equi­val­ence classes. As men­tioned earli­er, this part of the proof has ac­tu­ally been writ­ten down in a form­al lan­guage.

The rules cor­res­pond­ing to the first row in Fig­ure 7 were de­rived from an el­eg­ant meth­od of May­er and have the fol­low­ing geo­met­ric in­ter­pret­a­tion. Let \( v \in V (T ) \) have de­gree 5, and as­sume, as we may in the proof of The­or­em 12, that no good con­fig­ur­a­tion ap­pears in the second neigh­bor­hood of \( v \). The ver­tex \( v \) is ori­gin­ally as­signed a charge of 10. The rules in the first row are de­signed to send this charge from \( v \) to ver­tices of de­gree at least 7. Let \( e \) be an edge in­cid­ent with \( v \), let \( u \) be the oth­er end of \( e \), and let \( x \) be a com­mon neigh­bor of \( u \) and \( v \). Since \( T \) is in­tern­ally 6-con­nec­ted, there are ex­actly ten such pairs \( (e, x) \). For each such pair a charge of 1 will be sent away from \( v \) in­to a suit­able ver­tex, found as fol­lows. If the de­gree of \( u \) is at least 7, the unit of charge will be de­pos­ited in­to \( u \). Oth­er­wise, if \( x \) has de­gree at least 7, the unit of charge will be de­pos­ited in­to \( x \). Fi­nally, if both \( u \) and \( x \) have de­gree at most 6, let \[ z_1 = v, \,z_2 = u, \,z_3, \,z_4, \dots \] be the neigh­bors of \( x \) lis­ted in the or­der in which they ap­pear around \( x \). Since no good con­fig­ur­a­tion ap­pears in the second neigh­bor­hood of \( v \), one of these ver­tices has de­gree at least 7, as is eas­ily seen. Thus we may take the smal­lest in­teger \( i \geq 2 \) such that \( z_i \) has de­gree at least 7, and the unit of charge cor­res­pond­ing to \( (e, x) \) will be de­pos­ited in­to \( z_i \).

While this re­dis­tri­bu­tion of charges seems nat­ur­al, un­for­tu­nately it is not true that a re­du­cible con­fig­ur­a­tion ap­pears in the second neigh­bor­hood of every ver­tex of pos­it­ive charge. There­fore, we had to in­tro­duce ad­di­tion­al rules to make small changes to this dis­tri­bu­tion to take care of second neigh­bor­hoods of ver­tices with pos­it­ive charge in which no re­du­cible con­fig­ur­a­tion ap­peared. The ad­di­tion­al rules were ob­tained by tri­al and er­ror; there is a lot of flex­ib­il­ity in their choice, but they were not de­signed with any geo­met­ric in­tu­ition be­hind them.

The new proof of the 4CT gives hope that oth­er more gen­er­al con­jec­tures that are known to im­ply the 4CT could be settled by an ap­pro­pri­ate ad­apt­a­tion of the same meth­ods. Let me start by dis­cuss­ing a res­ult of my stu­dent Tom Fowl­er on unique col­or­ab­il­ity. A graph \( G \) is uniquely 4-col­or­able if it has a 4-col­or­ing and every two 4-col­or­ings dif­fer only by a per­muta­tion of col­ors. Here is a con­struc­tion. Start with the com­plete graph on four ver­tices. Giv­en a plane graph \( G \) con­struc­ted thus far, pick a tri­angle in \( G \), and add a new ver­tex ad­ja­cent to all ver­tices in­cid­ent with the tri­angle. It is easy to see that every graph con­struc­ted in this fash­ion is uniquely 4-col­or­able. Fiorini and Wilson con­jec­tured in 1977 that every uniquely 4-col­or­able plane graph on at least four ver­tices can be ob­tained this way. Fowl­er in his Ph.D. thes­is ex­ten­ded our proof of the 4CT to prove this con­jec­ture. More pre­cisely, he has shown

By The­or­em 10 this gen­er­al­izes the Four-Col­or The­or­em, and it im­plies the Fi­o­ri­ni–Wil­son con­jec­ture by a res­ult of Gold­was­ser and Zhang, who have shown that a min­im­al counter­example is in­tern­ally 6-con­nec­ted. (The proof of the lat­ter is ana­log­ous to that of The­or­em 10.)

While the 4CT be­comes false very quickly once we leave the world of planar graphs, Tutte no­ticed that The­or­em 3 re­mains true for a reas­on­ably large class of non­planar graphs. The smal­lest cu­bic graph with no cut-edge and no edge 3-co­lo­ring is the fam­ous Petersen graph de­pic­ted in Fig­ure 8. We say that a graph \( G \) has an \( H \) minor if a graph iso­morph­ic to \( H \) can be ob­tained from a sub­graph of \( G \) by con­tract­ing edges. Tutte con­jec­tured the fol­low­ing.

Tutte’s con­jec­ture im­plies the 4CT by The­or­em 3 (be­cause the Petersen graph is not planar, and con­trac­tion pre­serves pla­na­ri­ty), but it seems to be much stron­ger. However, it now ap­pears that there is a good chance that Tutte’s con­jec­ture can be proven. In­deed, Robertson, Sey­mour, and I have re­duced the prob­lem to the fol­low­ing two classes of graphs. We say that a graph \( G \) is apex if \( G\backslash v \) is planar for some ver­tex \( v \) of \( G \), and we say that a graph is doublecross if it can be drawn in the plane with two cross­ings in such a way that the two cross­ings be­long to the same re­gion (see Fig­ure 9). Robertson, Sey­mour, and I [e7] have shown the fol­low­ing.

Thus, in or­der to prove Con­jec­ture 14 it suf­fices to prove it for apex and doublecross graphs, two classes of graphs that are “al­most” planar. In fact, my re­cent work with Sanders sug­gests that it might be pos­sible to ad­apt our proof of the 4CT to show that no apex graph is a counter­example to Tutte’s con­jec­ture. There is an in­dic­a­tion that the doublecross case will be easi­er, but we can­not con­firm that yet.

There is a way to gen­er­al­ize the 4CT along the lines of (ver­tex) 4-col­or­ing. Had­wi­ger con­jec­tured the fol­low­ing.

This is trivi­al for \( t \leq 2 \), and for \( t = 3 \) it was shown by Had­wi­ger and Dir­ac (this case is also reas­on­ably easy). However, for every \( t \geq 4 \), Had­wi­ger’s con­jec­ture im­plies the 4CT. To see this, take a plane graph \( G \), and con­struct a graph \( H \) by adding \( t - 4 \) ver­tices ad­ja­cent to each oth­er and to every ver­tex of \( G \). Then \( H \) has no \( K_{t+1} \) minor (be­cause no plane graph has a \( K_5 \) minor) and hence has a \( t \)-col­or­ing by the as­sumed truth of Had­wi­ger’s con­jec­ture. In this \( t \)-col­or­ing, ver­tices of \( G \) are colored us­ing at most four col­ors, as re­quired. Thus there is a rather sharp in­crease in the level of dif­fi­culty of Had­wi­ger’s con­jec­ture between \( t = 3 \) and \( t = 4 \). On the oth­er hand, Wag­n­er showed in 1937 that Had­wi­ger’s con­jec­ture for \( t = 4 \) is in fact equi­val­ent to the 4CT. (No­tice that this res­ult pre­ceded the proof of the 4CT by four dec­ades and, in fact, in­spired Had­wi­ger’s con­jec­ture.) Re­cently, Robertson, Sey­mour, and I were able to show that the next case is also equi­val­ent to the 4CT [e4]. More pre­cisely, we man­aged to prove (without us­ing the 4CT) the fol­low­ing.

By the 4CT every apex graph has a 5-col­or­ing, and so Had­wi­ger’s con­jec­ture for \( t = 5 \) fol­lows. The cases \( t \geq 6 \) are still open.