Celebratio Mathematica — Baum

Twisted K-homology and Paul Baum

by Alan L. Carey

1. Preamble

It may seem hard to believe but I am not exactly sure when I first met Paul. However the occasion of a meeting organised by David Evans in 1987 in Warwick may well qualify. Our first substantial mathematical interaction, however, did not occur until an Oxford meeting organised by John Roe in the early 90s. There Paul, Varghese Mathai and I enjoyed a number of entertaining conversations and Paul made some very helpful comments which played a role in securing Mathai a prestigious Australian Research Council Fellowship soon after. Paul has been to Australia on several occasions visiting Sydney, Melbourne, Newcastle and finally Canberra. He achieved some notoriety for breaking into song at the Australian Mathematical Society conference dinner in La Trobe University in 2007. He was in very good spirits after giving the best plenary of the meeting a day or two beforehand. Paul was awarded an honorary doctorate from the Australian National University in 2013 in recognition of his lengthy and significant support of Australian mathematicians.

Our substantial research interaction began in Texas Christian University at a meeting in honour of Jonathan Rosenberg. Before launching into that it is useful to recall some history of twisted K-theory and this will occupy the next section. After that I will cover the basics on twisted K-theory. Then in the main section of the paper I will describe twisted geometric cycles from two viewpoints, BB (before Baum) and AB (after Baum). The story ends on a happy note.

2. History

The story brings together a number of mathematical topics: gerbes, continuous trace $C^{*}$ algebras, K-homology (both analytic and geometric) and $D$ -branes from string theory. This is a broad set of topics but they all fit into the jigsaw puzzle.

Continuous trace algebras have their roots in work of Grothendieck [e3] and Dixmier and Douady [e1], who studied bundles of algebras over a paracompact space $X$ with fibre either a matrix algebra or the compact operators on an infinite-dimensional Hilbert space. They are characterised by an associated invariant; a class in degree-3 Čech cohomology of the base was identified (it is now known as the Dixmier–Douady class). From these papers two independent lines of development began. The first, the theory of gerbes, began with [e5] and was extended and applied to problems in string theory in [e13].

The other line of development is the theory of continuous trace $C^{*}$ -algebras. These are algebras of sections of the bundles introduced by Dixmier and Douady. Their history can be found in the monograph of Raeburn and Williams [e17].

Twisted K-theory now comes into the picture. Given a paracompact space $X$ with a “twist”, namely a degree-3 cohomology class $[α]$ on $X,$ there is a principal bundle with fibre the projective unitary group of a separable Hilbert space over $X$ characterised by $[α] .$ Now regard the projective unitary group as the automorphism group of the compact operators on this Hilbert space. Then, following Rosenberg [e10], the twisted K-theory of $X$ is the K-theory of the continuous trace $C^{*}$ -algebra of sections of the bundle over $X$ associated to the given principal bundle with twist $[α] .$ The twist only specifies an equivalence class of continuous trace algebras, so this means that twisted K-theory with twist $[α]$ is only defined by this method up to an isomorphism.

These two disparate lines formed the motivation for the work of Murray [e15] on bundle gerbes. Bundle gerbes provide a differential geometric way to approach twisted K-theory, as explained in [e24], that is closely aligned with the geometry that is used in string theory.

The additional ingredient in this picture that we need from the string theory side is the notion of $D$ -branes [e14]. They were proposed as a mechanism for providing boundary conditions for the dynamics of open strings moving in space-time. Initially they were thought of as submanifolds. As $D$ -branes themselves can evolve over time, one needs to study equivalence relations on the set of $D$ -branes. An invariant of the equivalence class is the topological charge of the $D$ -brane, which should be thought of as an analogue of the Dirac monopole charge as these $D$ -brane charges are associated with gauge fields (connections) on vector bundles over the $D$ -brane. These vector bundles are known as Chan–Paton bundles.

In [e16] Minasian and Moore made the proposal that $D$ -brane charges should take values in K-groups and not in the cohomology of the space-time or the $D$ -brane. However, they proposed a cohomological formula for these charges which might be thought of as a kind of index theorem in the sense that, in general, index theory associates to a K-theory class a number which is given by an integral of a closed differential form. In string theory there is an additional field on space-time known as the $H$ -flux which may be thought of as a global closed 3-form. Locally it is given by a family of “2-form potentials” known as the $B$ -field. Mathematically these $B$ -fields are in fact defining a degree-3 integral Čech class on the space-time, that is, the “twist”. Witten [e18], extending [e16], gave a physical argument for the idea that $D$ -brane charges should be elements of K-groups and, in addition, proposed that the $D$ -brane charges in the presence of a twist should take values in twisted K-theory (at least in the case where the twist is torsion). The mathematical ideas he relied on were due to Donovan and Karoubi [e4]. Subsequently Bouwknegt and [e20] extended Witten’s proposal to the nontorsion case using ideas from [e10]. A geometric model (that is, a “string geometry” picture) for some of these string theory constructions and for twisted K-theory was proposed in [e24] using the notion of bundle gerbes and bundle gerbe modules. Various refinements of twisted K-theory that are suggested by these applications are also described in the article of Atiyah and Segal [e27] and their ideas play a role in the next development.

2.1 Mathematical perspective

The contributions of physicists raise some immediate questions. When there is no twist, the relationship between K-theory and index theory of elliptic operators is now well-established, including the geometric cycle approach to K-homology. In fact one version of the Atiyah–Singer index theorem due to Baum, Higson, and Schick [3] establishes a relationship between the analytic viewpoint provided by elliptic differential operators and the geometric viewpoint provided by the notion of geometric cycle introduced in the fundamental paper of Baum and Douglas [1]. The viewpoint that geometric cycles in the sense of [1] are a model for $D$ -branes in the untwisted case is expounded in [e29], [e36], [e34]. Note that in this viewpoint $D$ -branes are no longer submanifolds (as envisaged originally by physicists) but the images of manifolds under a smooth map.

It is thus tempting to conjecture that there is an analogous picture of $D$ -branes as a type of geometric cycle in the twisted case as well. More precisely the question is whether there is a way to formulate the notion of “twisted geometric cycle” (in analogy with [2] and [1]) and to prove an index theorem in the spirit of [3] for twisted K-homology. An approach to answering this question was proposed in [e33], though there is a step in the proof that is omitted. Wang understood that the missing step requires a twisted version of the Conner–Floyd splitting theorem [e7] for ${Spin}^{c}$ -bordism; however a complete version of Bai-Ling Wang’s argument has not appeared. The good news is that there is an argument that is similar in spirit to what Wang proposed due to Paul and collaborators that overcomes not just this one difficulty but provides a construction of twisted K-homology for CW-complexes [5]. In the last section we will describe briefly this new approach that is in preparation. It is important to emphasise that string geometry ideas from [e19] played a key role in finding the correct way to generalise [2].

In this enterprise, Paul entered the picture via his interaction with Bai-Ling Wang over the ideas introduced in [e33]. I want to explain this in detail in this essay. I will also fill in many of the details for the matters discussed previously in this introduction. I have borrowed very freely from a review article that I wrote with Bai-Ling Wang after our meeting with Paul in Texas Christian University [e37] (though whether it was an epiphany is hard to determine).

It is essential to remark that none of the existing arguments that are used in the geometric cycle approach to index theory (the general index problem of Paul) extend to cover the twisted version for CW-complexes. In the final section I am pleased to announce that there is now a very general argument that applies to all instances.

This article contains nothing original but does draw together the many threads that have led us to the present understanding of K-homology in the twisted case.

3. Topological and analytic twisted K-theory

Though our focus is twisted K-homology, in the literature on this topic, extensive use is made of Poincaré duality. For this reason it is important to review first some aspects of twisted K-theory.

We begin with the notion of a “twisting”. Let $H$ be an infinite-dimensional, complex and separable Hilbert space. We shall consider locally trivial principal $PU (H)$ -bundles over a paracompact Hausdorff topological space $X;$ the structure group $PU (H)$ is equipped with the norm topology. The projective unitary group $PU (H)$ with the topology induced by the norm topology on $U (H)$ (see [e2]) has the homotopy type of an Eilenberg–MacLane space $K (Z, 2) .$ The classifying space of $PU (H),$ denoted by $BPU (H),$ is a $K (Z, 3) .$ The set of isomorphism classes of principal $PU (H)$ -bundles over $X$ is given by (Proposition 2.1 in [e27]) homotopy classes of maps from $X$ to any $K (Z, 3)$ and there is a canonical identification $[X, BPU (H)] ≅ H^{3} (X, Z) .$

A twisting of complex K-theory on $X$ is given by a continuous map $α : X \to K (Z, 3) .$ For such a twisting, we can associate a canonical principal $PU (H)$ -bundle $P_{α}$ through the usual pull-back construction from the universal $PU (H)$ bundle denoted by $E K (Z, 2),$ as summarised by the diagram $\begin{matrix} (1) & \begin{matrix} P_{α} & \to_{}^{} & E K (Z, 2) \\ ↓ & ↓ \\ X & \to_{α}^{} & K (Z, 3) \end{matrix} \end{matrix}$ We will use $PU (H)$ as a group model for a $K (Z, 2) .$ We write $Fred (H)$ for the connected component of the identity of the space of Fredholm operators on $H$ equipped with the norm topology. There is a base-point-preserving action of $PU (H)$ given by the conjugation action of $U (H)$ on $Fred (H) :$ $\begin{matrix} (2) & PU (H) \times Fred (H) ⟶ Fred (H) . \end{matrix}$

The action $(2)$ defines an associated bundle over $X$ which we denote by $P_{α} (Fred) = P_{α} \times_{PU (H)} Fred (H) .$ We write ${Ω_{X}^{n} P_{α} (Fred) = P_{α} \times_{PU (H)} Ω^{n} Fred}$ for the fibre-wise iterated loop spaces.

Definition: The (topological) twisted K-groups of $(X, α)$ are defined to be $K^{- n} (X, α) := π_{0} (C_{c} (X, Ω_{X}^{n} P_{α} (Fred))),$ the set of homotopy classes of compactly supported sections (meaning they are the identity operator in $Fred$ off a compact set) of the bundle of $P_{α} (Fred) .$

Due to Bott periodicity, we only have two different twisted K-groups $K^{0} (X, α)$ and $K^{1} (X, α) .$ Given a closed subspace $A$ of $X,$ $(X, A)$ is a pair of topological spaces, and we define relative twisted K-groups to be $K^{ev / odd} (X, A; α) := K^{ev / odd} (X - A, α) .$

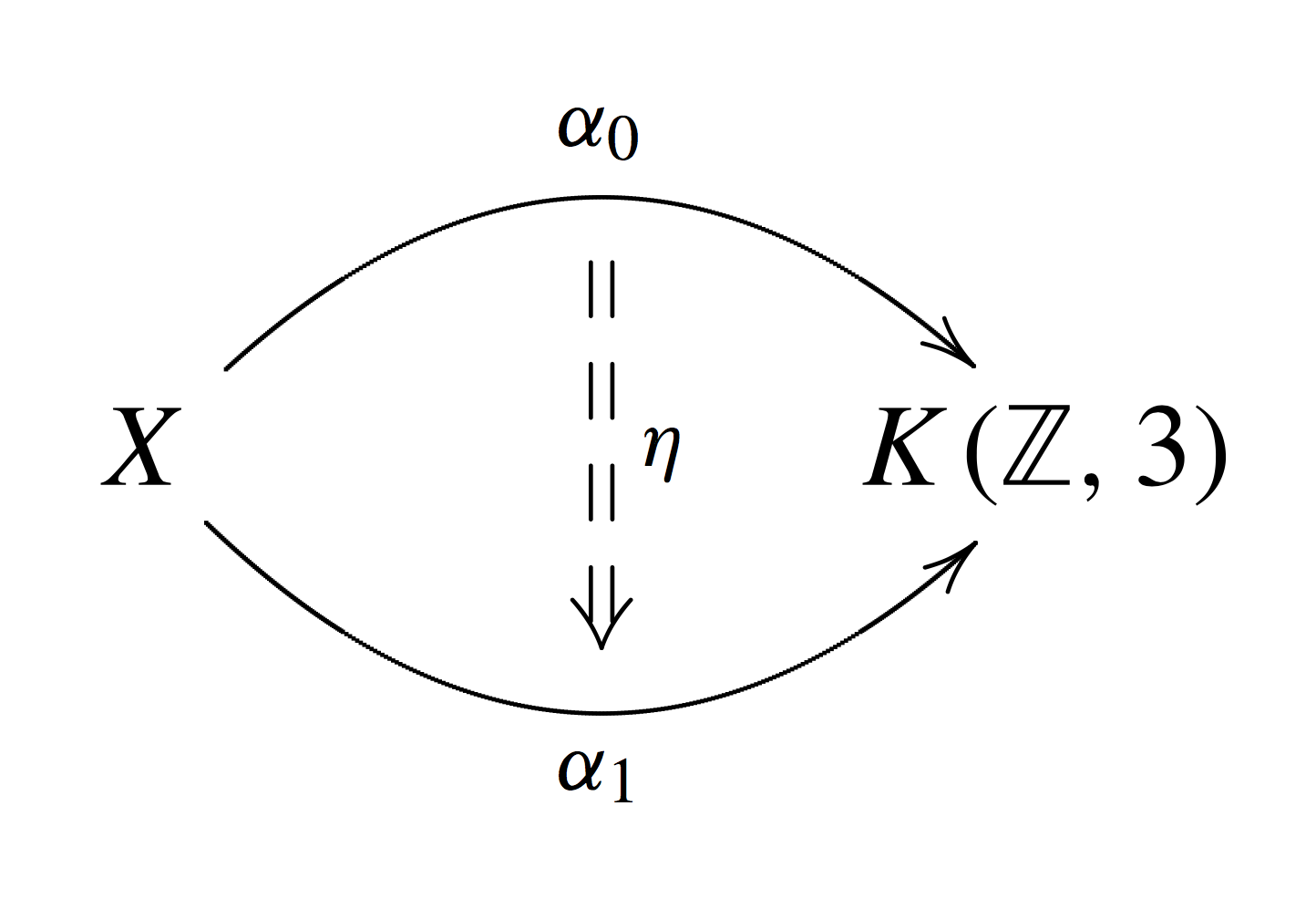
Take a pair of twistings $α_{0}, α_{1} : X ⟶ K (Z, 3),$ and a map $η : X \times [1, 0] ⟶ K (Z, 3)$ which is a homotopy between $α_{0}$ and $α_{1},$ represented diagrammatically by the figure shown to the right. Then there is a canonical isomorphism $P_{α_{0}} ≅ P_{α_{1}}$ induced by $η .$ This canonical isomorphism determines a canonical isomorphism on twisted K-groups $\begin{matrix} (3) & η_{*} : K^{ev / odd} (X, α_{0}) \overset{≅}{\to} K^{ev / odd} (X, α_{1}) . \end{matrix}$ This isomorphism $η_{*}$ depends only on the homotopy class of $η .$ The set of homotopy classes of maps between $α_{0}$ and $α_{1}$ is labelled by $[X, K (Z, 2)] .$ Recall the first Chern class isomorphism ${Vect}_{1} (X) ≅ [X, K (Z, 2)] ≅ H^{2} (X, Z),$ where ${Vect}_{1} (X)$ is the set of equivalence classes of complex line bundles on $X .$ We remark that the isomorphisms induced by two different homotopies between $α_{0}$ and $α_{1}$ are related through an action of complex line bundles.

Let $K$ be the $C^{*}$ -algebra of compact operators on $H .$ The isomorphism $PU (H) ≅ Aut (K)$ via the conjugation action of the unitary group $U (H)$ provides an action of a $K (Z, 2)$ on the $C^{*}$ -algebra $K .$ Hence, any $K (Z, 2)$ -principal bundle $P_{α}$ defines a locally trivial bundle of compact operators, denoted by $P_{α} (K) = P_{α} \times_{PU (H)} K .$

Let $Γ_{0} (X, P_{α} (K))$ be the $C^{*}$ -algebra of sections of $P_{α} (K)$ vanishing at infinity. Then $Γ_{0} (X, P_{α} (K)$ is the (unique up to isomorphism) stable separable complex continuous-trace $C^{*}$ -algebra over $X$ with Dixmier–Douady class $[α] \in H^{3} (X, Z)$ (here we identify the Čech cohomology of $X$ with its singular cohomology; see [e10] and [e27]).

Theorem 1 ([e27],[e10]): The topological twisted K-groups

K^{ev / odd} (X, α)

are canonically isomorphic to analytic K-theory of the

C^{*}

-algebra

Γ_{0} (X, P_{α} (K))

K^{ev / odd} (X, α) ≅ K_{ev / odd} (Γ_{0} (X, P_{α} (K))),

where the latter group is the K-theory of

Γ_{0} (X, P_{α} (K)),

defined to be

\underset{k \to \infty}{\lim_{\to}} π_{1} ({GL}_{k} (Γ_{0} (X, P_{α} (K)))) .

Note that the K-theory of

Γ_{0} (X, P_{α} (K))

is isomorphic to Kasparov’s

K K

-theory [e6], [e9], [e8]

K K^{ev / odd} (C, Γ_{0} (X, P_{α} (K)) .

It is important to recognise that these groups are only defined up to isomorphism by the Dixmier–Douady class $[α] \in H^{3} (X, Z) .$ To distinguish these two definitions of twisted K-theory we will write $K_{top}^{ev / odd} (X, α)$ and $K_{an}^{ev / odd} (X, α)$ for the topological and analytic twisted K-theories of $(X, α)$ respectively. Twisted K-theory is a 2-periodic generalised cohomology theory: a contravariant functor on the category consisting of pairs $(X, α),$ with the twisting $α : X \to K (Z, 3),$ to the category of $Z_{2}$ -graded abelian groups. Note that a morphism between two pairs $(X, α)$ and $(Y, β)$ is a continuous map $f : X \to Y$ such that $β \circ f = α .$

3.1. Twisted K-theory for torsion twistings

There are some subtle issues in twisted K-theory and to handle these we have chosen to use the language of bundle gerbes, connections and curvings as explained in [e15]. We explain first the so-called “lifting bundle gerbe” $G_{α}$ [e15] associated to the principal $PU (H)$ -bundle $π : P_{α} \to X$ and the central extension $\begin{matrix} (4) & 1 \to U (1) ⟶ U (H) ⟶ PU (H) \to 1. \end{matrix}$ This is constructed by starting with $π : P_{α} \to X,$ forming the fibre product $P_{α}^{[2]},$ which is a groupoid $P_{α}^{[2]} = P_{α} \times_{X} P_{α} \begin{matrix} \overset{π_{1}}{\to} \\ \to_{π_{2}}^{} \end{matrix} P_{α}$ with source and range maps $π_{1} : (y_{1}, y_{2}) ⟼ y_{1} and π_{2} : (y_{1}, y_{2}) ⟼ y_{2} .$ There is an obvious map from each fibre of $P_{α}^{[2]}$ to $PU (H)$ and so we can define the fibre of $G_{α}$ over a point in $P_{α}^{[2]}$ by pulling back the fibration $(4)$ using this map. This endows $G_{α}$ with a groupoid structure (from the multiplication in $U (H)$ ) and in fact it is a $U (1)$ -groupoid extension of $P_{α}^{[2]} .$

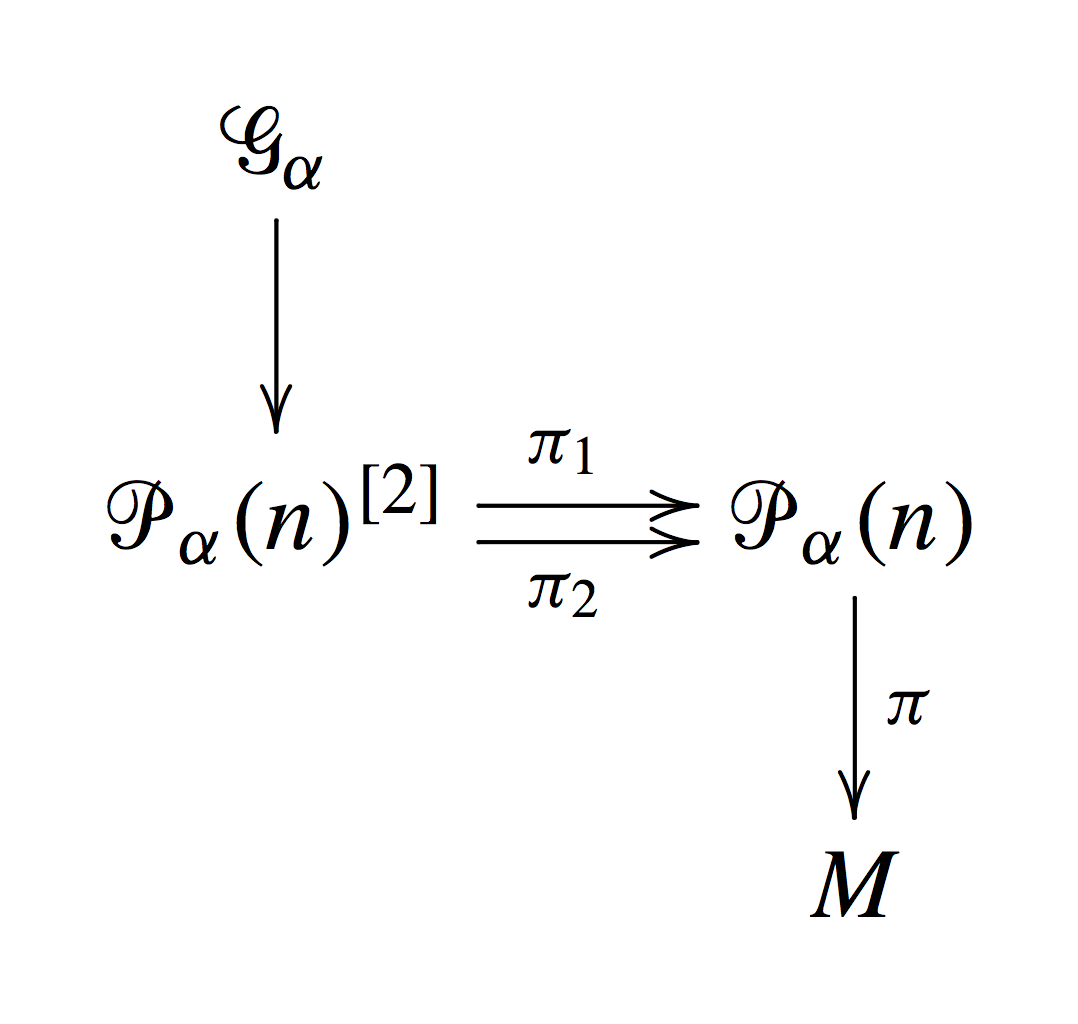
A torsion twisting $α$ is a map $α : X \to K (Z, 3)$ representing a torsion class in $H^{3} (X, Z) .$ Every torsion twisting arises from a principal $PU (n)$ -bundle $P_{α} (n)$ with its classifying map $X \to BPU (n),$ or a principal $PU (H)$ -bundle with a reduction to $PU (n) \subset PU (H) .$ For a torsion twisting $α : X ⟶ BPU (n) ⟶ BPU (H),$ the corresponding lifting bundle gerbe $G_{a}$ shown to the right is defined by $P_{α} (n)^{[2]} ≅ P_{α} (n) ⋊ PU (n) ⇉ P_{α} (n)$ (as a groupoid) and the central extension $1 \to U (1) ⟶ U (n) ⟶ PU (n) \to 1.$

There is an Azumaya bundle associated to $P_{α} (n)$ arising naturally from the $PU (n)$ action on the $n \times n$ matrices. We denote this associated Azumaya bundle by $A_{α} .$ An $A_{α}$ -module is a complex vector bundle $E$ over $M$ with a fibre-wise $A_{α}$ action $A_{σ} \times_{M} E ⟶ E .$ The $C^{*}$ -algebra of continuous sections of $A_{α},$ vanishing at infinity if $X$ is noncompact, is Morita equivalent to a continuous trace $C^{*}$ -algebra $Γ_{0} (X, P_{α} (K)) .$ Hence there is an isomorphism between $K^{0} (X, α)$ and the K-theory of the bundle modules of $A_{a} .$

There is an equivalent definition of twisted K-theory using bundle gerbe modules (see [e24] and [e32]). A bundle gerbe module $E$ of $G_{α}$ is a complex vector bundle $E$ over $P_{α} (n)$ with a groupoid action of $G_{α},$ i.e., an isomorphism $φ : G_{α} \times_{(π_{2}, p)} E ⟶ E,$ where $G_{α} \times_{(π_{2}, π)} E$ is the fibre product of the source $π_{2} : G_{α} \to P_{α} (n) and p : E \to P_{α} (n)$ such that

$p \circ φ (g, v) = π_{1} (g)$ for $(g, v) \in G_{α} \times_{(π_{2}, p)} E,$ and $π_{1}$ is the target map of $G_{α};$
$φ$ is compatible with the bundle gerbe multiplication $m : G_{a} \times_{(π_{2}, π_{1})} G_{α} \to G_{α},$ which means $φ \circ (id \times φ) = φ \circ (m \times id) .$

Note that the natural representation of $U (n)$ on $C^{n}$ induces a $G_{α}$ bundle gerbe module $S_{n} = P_{α} (n) \times C^{n} .$ Here we use the fact that $G_{α} = P_{α} (n) ⋊ U (n) ⇉ P_{α} (n)$ (as a groupoid). Similarly, the dual representation of $U (n)$ on $C^{n}$ induces a $G_{- α}$ bundle gerbe module $S_{n}^{*} = P_{α} (n) \times C^{n} .$ Note that $S_{n}^{*} \otimes S_{n} ≅ π^{*} A_{α}$ descends to the Azumaya bundle $A_{α} .$ Given a $G_{α}$ bundle gerbe module $E$ of rank K, as a $PU (n)$ -equivariant vector bundle, $S_{n}^{*} \otimes E$ descends to an $A_{α}$ -bundle over $M .$ Conversely, given an $A_{α}$ -bundle $E$ over $M,$ $S_{n} \otimes_{π^{*} A_{α}} π^{*} E$ defines a $G_{α}$ bundle gerbe module. These two constructions are inverse to each other due to the fact that $\begin{aligned} S_{n}^{*} \otimes (S_{n} \otimes_{π^{*} A_{α}} π^{*} E) & ≅ (S_{n}^{*} \otimes S_{n}) \otimes_{π^{*} A_{α}} π^{*} E \\ ≅ π^{*} A_{α} \otimes_{π^{*} A_{α}} π^{*} E \\ ≅ π^{*} E . \end{aligned}$ Therefore, there is a natural equivalence between the category of $G_{α}$ bundle gerbe modules and the category of $A_{α}$ bundle modules, as discussed in [e32]. In summary, we have the following proposition.

Proposition 2 ([e24],[e32]): For a torsion twisting

α : X ⟶ BPU (n) ⟶ BPU (H),

twisted K-theory

K^{0} (X, α)

has another two equivalent descriptions:

the Grothendieck group of the category of $G_{α}$ bundle gerbe modules,
the Grothendieck group of the category of $A_{σ}$ bundle modules.

One important example of torsion twistings comes from real oriented vector bundles. Consider an oriented real vector bundle $E$ of even rank over $X$ with a fixed fibre-wise inner product. Denote by $ν_{E} : X \to BSO (2 k)$ the classifying map of $E .$ The twisting $o (E) := W_{3} \circ ν_{E} : X ⟶ BSO (2 k) ⟶ K (Z, 3)$ will be called the orientation twisting associated to $E .$ Here $W_{3}$ is the classifying map of the principal $BU (1)$ -bundle ${BSpin}^{c} (2 k) \to BSO (2 k) .$ Note that the orientation twisting $o (E)$ is null-homotopic if and only if $E$ is K-oriented.

Proposition 3: Given an oriented real vector bundle

E

of even rank over

X

with an orientation twisting

o (E),

there is a canonical isomorphism

K^{0} (X, o (E)) ≅ K^{0} (X, W_{3} (E)),

where

K^{0} (X, W_{3} (E))

is the K-theory of the Clifford modules associated to the bundle

Cliff (E)

of Clifford algebras.

Proof. Denote by $F r$ the frame bundle of $V,$ the principal $SO (2 k)$ -bundle of positively oriented orthonormal frames, i.e., $E = F r \times_{ρ_{2 n}} R^{2 k},$ where $ρ_{n}$ is the standard representation of $SO (2 k)$ on $R^{n} .$ The lifting bundle gerbe associated to the frame bundle and the central extension $1 \to U (1) ⟶ {Spin}^{c} (2 k) ⟶ SO (2 k) \to 1$ is called the ${Spin}^{c}$ bundle gerbe $G_{W_{3} (E)}$ of $E,$ whose Dixmier–Douady invariant is given by the integral third Stiefel–Whitney class $W_{3} (E) \in H^{3} (X, Z) .$ The canonical representation of ${Spin}^{c} (2 k)$ gives a natural inclusion ${Spin}^{c} (2 k) \subset U (2^{k})$ which induces a commutative diagram $\begin{matrix} U (1) & \to_{}^{} & {Spin}^{c} (2 k) & \to_{}^{} & SO (2 k) \\ ↓ = & ↓ & ↓ \\ U (1) & \to_{}^{} & U (2^{k}) & \to_{}^{} & PU (2^{k}) \\ ↓ = & ↓ & ↓ \\ U (1) & \to_{}^{} & U (H) & \to_{}^{} & PU (H) \end{matrix}$ This provides a reduction of the principal $PU (H)$ -bundle $P_{o (E)} .$ The associated bundle of Azumaya algebras is in fact the bundle of Clifford algebras, whose bundle modules are called Clifford modules [e12]. Hence, there exists a canonical isomorphism between $K^{0} (X, o (E))$ and the K-theory of the Clifford modules associated to the bundle $Cliff (E) .$ ☐

4. Topological and analytic twisted K-homology

Let $X$ be a CW-complex (or paracompact Hausdorff space) with a twisting $α : X \to K (Z, 3)$ and $P_{α}$ be the corresponding principal $K (Z, 2)$ -bundle. Any base-point-preserving action of a $K (Z, 2)$ on a space defines an associated bundle by the standard construction. In particular, as a classifying space of complex line bundles, $K (Z, 2)$ acts on the complex K-theory spectrum $K$ representing the tensor product by complex line bundles, where $K_{ev} = Z \times BU (\infty), K_{odd} = U (\infty) .$ Denote by $P_{α} (K) = P_{α} \times_{K (Z, 2)} K$ the bundle of based K-theory spectra over $X .$ There is a section of $P_{α} (K) = P_{α} \times_{K (Z, 2)} K$ defined by taking the base points of each fibre. The image of this section can be identified with $X$ and we denote by $P_{α} (K) / X$ the quotient space of $P_{α} (K)$ obtained by collapsing the image of this section.

The stable homotopy groups of $P_{α} (K) / X$ by definition give the topological twisted K-homology groups $K_{ev / odd}^{top} (X, α) .$ (There are only two due to Bott periodicity of $K .$ ) Thus we have $K_{ev}^{top} (X, α) = \underset{k \to \infty}{\lim_{\to}} π_{2 k} (P_{α} (BU (\infty)) / X)$ and $K_{odd}^{top} (X, α) = \underset{k \to \infty}{\lim_{\to}} π_{2 k + 1} (P_{α} (BU (\infty)) / X) .$ Here the direct limits are taken by the double suspension $π_{n + 2 k} (P_{α} (BU (\infty)) / X) ⟶ π_{n + 2 k + 2} (P_{α} (S^{2} \land BU (\infty)) / X)$ and then followed by the standard map $\begin{aligned} π_{n + 2 k + 2} (P_{α} (S^{2} \land BU (\infty)) / X) & \overset{b \land 1}{\to} π_{n + 2 k + 2} (P_{α} (BU (\infty) \land BU (\infty)) / X) \\ \overset{m}{\to} π_{n + 2 k + 2} (P_{α} (BU (\infty)) / X), \end{aligned}$ where $b : R^{2} \to BU (\infty)$ represents the Bott generator in $K^{0} (R^{2}) ≅ Z,$ $m$ is the base-point-preserving map inducing the ring structure on K-theory.

For a relative CW-complex $(X, A)$ with a twisting $α : X \to K (Z, 3),$ the relative version of topological twisted K-homology, denoted by $K_{ev / odd}^{top} (X, A, α),$ is defined to be $K_{ev / odd}^{top} (X / A, α),$ where $X / A$ is the quotient space of $X$ obtained by collapsing $A$ to a point. Then we have the exact sequence $\begin{matrix} K_{odd}^{top} (X, A; α) & \to_{}^{} & K_{ev}^{top} (A, α |_{A}) & \to_{}^{} & K_{ev}^{top} (X, α) \\ ↑ & ↓ \\ K_{odd}^{top} (X, α) & \leftarrow_{}^{} & K_{odd}^{top} (A, α |_{A}) & \leftarrow_{}^{} & K_{ev}^{top} (X, A; α) \end{matrix}$ and the excision properties $K_{ev / odd}^{top} (X, B; α) ≅ K_{ev / odd}^{top} (A, A - B; α |_{A})$ for any CW-triad $(X; A, B)$ with a twisting $α : X \to K (Z, 3) .$ A triple $(X; A, B)$ is a CW-triad if $X$ is a CW-complex, and $A,$ $B$ are two subcomplexes of $X$ such that $A \cup B = X .$

Analytic twisted K-homology, denoted by $K_{ev / odd}^{an} (X, α),$ is defined to be $K_{ev / odd}^{an} (X, α) := K K^{ev / odd} (Γ_{0} (X, P_{α} (K)), C),$ Kasparov’s $Z_{2}$ -graded K-homology of the $C^{*}$ -algebra $Γ_{0} (X, P_{α} (K)) .$

For a relative CW-complex $(X, A)$ with a twisting $α : X \to K (Z, 3),$ the relative version of analytic twisted K-homology $K_{ev / odd}^{an} (X, A, α)$ is defined to be $K_{ev / odd}^{an} (X - A, α) .$ Then we have the exact sequence $\begin{matrix} K_{odd}^{an} (X, A; α) & \to_{}^{} & K_{ev}^{an} (A, α |_{A}) & \to_{}^{} & K_{ev}^{an} (X, α) \\ ↑ & ↓ \\ K_{odd}^{an} (X, α) & \leftarrow_{}^{} & K_{odd}^{an} (A, α |_{A}) & \leftarrow_{}^{} & K_{ev}^{an} (X, A; α) \end{matrix}$ and the excision properties $K_{ev / odd}^{an} (X, B; α) ≅ K_{ev / odd}^{an} (A, A - B; α |_{A})$ for any CW-triad $(X; A, B)$ with a twisting $α : X \to K (Z, 3) .$

Theorem 4 (Theorem 5.1 in [e33]): There is a natural isomorphism

Φ : K_{ev / odd}^{top} (X, α) ⟶ K_{ev / odd}^{an} (X, α)

for any smooth manifold

X

with a twisting

α : X \to K (Z, 3) .

The proof of this theorem requires Poincaré duality between twisted K-theory and twisted K-homology (we describe this duality in the next theorem), and the isomorphism (Theorem 1) between topological twisted K-theory and analytic twisted K-theory.

Fix an isomorphism $H \otimes H ≅ H$ which induces a group homomorphism $U (H) \times U (H) \to U (H)$ whose restriction to the centre is the group multiplication on $U (1) .$ So we have a group homomorphism $PU (H) \times PU (H) ⟶ PU (H)$ which defines a continuous map, denoted by $m_{*},$ of CW-complexes $BPU (H) \times B P U (H) ⟶ BPU (H) .$ As $BPU (H)$ is identified as $K (Z, 3),$ we may think of this as a continuous map taking $K (Z, 3) \times K (Z, 3) to K (Z, 3),$ which can be used to define $α + o_{X} .$

There are natural isomorphisms from twisted K-homology (topological, resp. analytic) to twisted K-theory (topological, resp. analytic) of a smooth manifold $X$ where the twisting is shifted by $α \mapsto α + o_{X},$ where $τ : X \to BSO$ is the classifying map of the stable tangent space and $α + o_{X}$ denotes the map $X \to K (Z, 3),$ representing the class $[α] + W_{3} (X) in H^{3} (X, Z) .$

Theorem 5: Let

X

be a smooth manifold with a twisting

α : X \to K (Z, 3) .

There exist isomorphisms

K_{ev / odd}^{top} (X, α) ≅ K_{top}^{ev / odd} (X, α + o_{X})

and

K_{ev / odd}^{an} (X, α) ≅ K_{an}^{ev / odd} (X, α + o_{X}),

with the degree shifted by

\dim X (\mod 2) .

Analytic Poincaré duality was established in [e31] and [e35], and topological Poincaré duality was established in [e33]. Theorem 4 and the exact sequences for a pair $(X, A)$ imply the following corollary.

Corollary 6: There is a natural isomorphism

Φ : K_{ev / odd}^{top} (X, A, α) ⟶ K_{ev / odd}^{an} (X, A, α)

for any smooth manifold

X

with a twisting

α : X \to K (Z, 3)

and a closed submanifold

A \subset X .

Remark: In fact, Poincaré duality as in Theorem 5 holds for any compact Riemannian manifold $W$ with boundary $\partial W$ and a twisting $α : W \to K (Z, 3) .$ This duality takes the form $K_{ev / odd}^{top} (W, α) ≅ K_{top}^{ev / odd} (W, \partial W, α + o_{W})$ and $K_{ev / odd}^{an} (W, α) ≅ K_{an}^{ev / odd} (X, \partial X, α + o_{W}),$ with the degree shifted by $\dim W (\mod 2) .$ From this, we have a natural isomorphism $Φ : K_{ev / odd}^{top} (X, A, α) ⟶ K_{ev / odd}^{an} (X, A, α)$ for any CW pair $(X, A)$ with a twisting $α : X \to K (Z, 3)$ using the five lemma.

5. Geometric cycles and geometric twisted K-homology

This is the main section of this essay. Here we outline both the ideas due to Bai-Ling Wang and the ideas due mostly to Paul. One may easily move between these points of view.

As usual $X$ is a paracompact Hausdorff space and $α : X \to K (Z, 3)$ is a twisting over $X .$

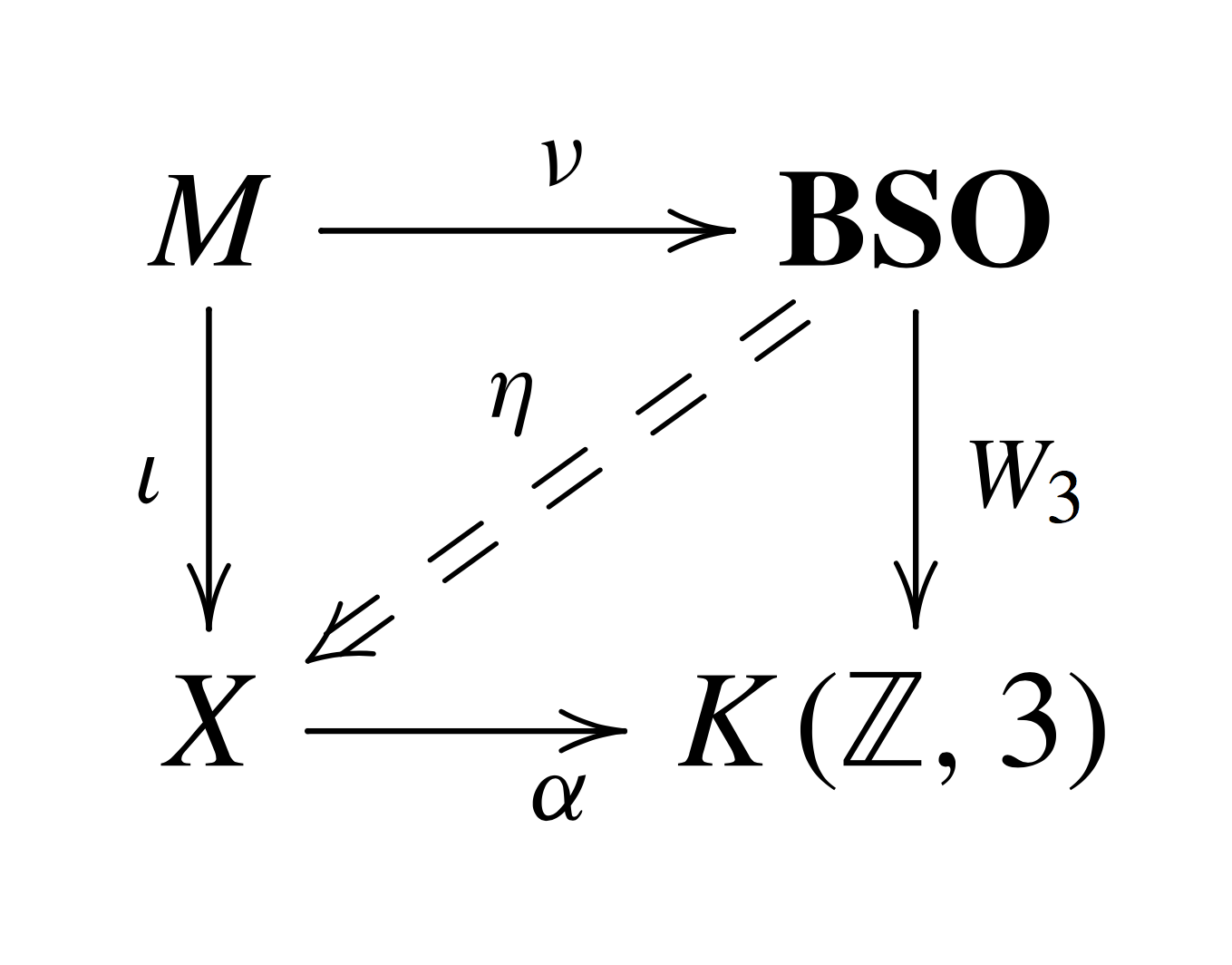
Definition: Given a smooth oriented manifold $M$ with a classifying map $ν$ of its stable normal bundle, we say that $M$ is an $α$ -twisted ${Spin}^{c}$ manifold over $X$ if $M$ is equipped with an $α$ -twisted ${Spin}^{c}$ structure, that means, a continuous map $ι : M \to X$ such that the diagram shown to the right commutes up to a fixed homotopy $η$ from $W_{3} \circ ν$ and $α \circ ι .$ Such an $α$ -twisted ${Spin}^{c}$ manifold over $X$ will be denoted by $(M, ν, ι, η) .$

Proposition 7:

M

admits an

α

-twisted

{Spin}^{c}

structure if and only if there is a continuous map

ι : M \to X

such that

ι^{*} ([α]) + W_{3} (M) = 0.

ι

is an embedding, this is the anomaly cancellation condition obtained by Freed and Witten in [e19].

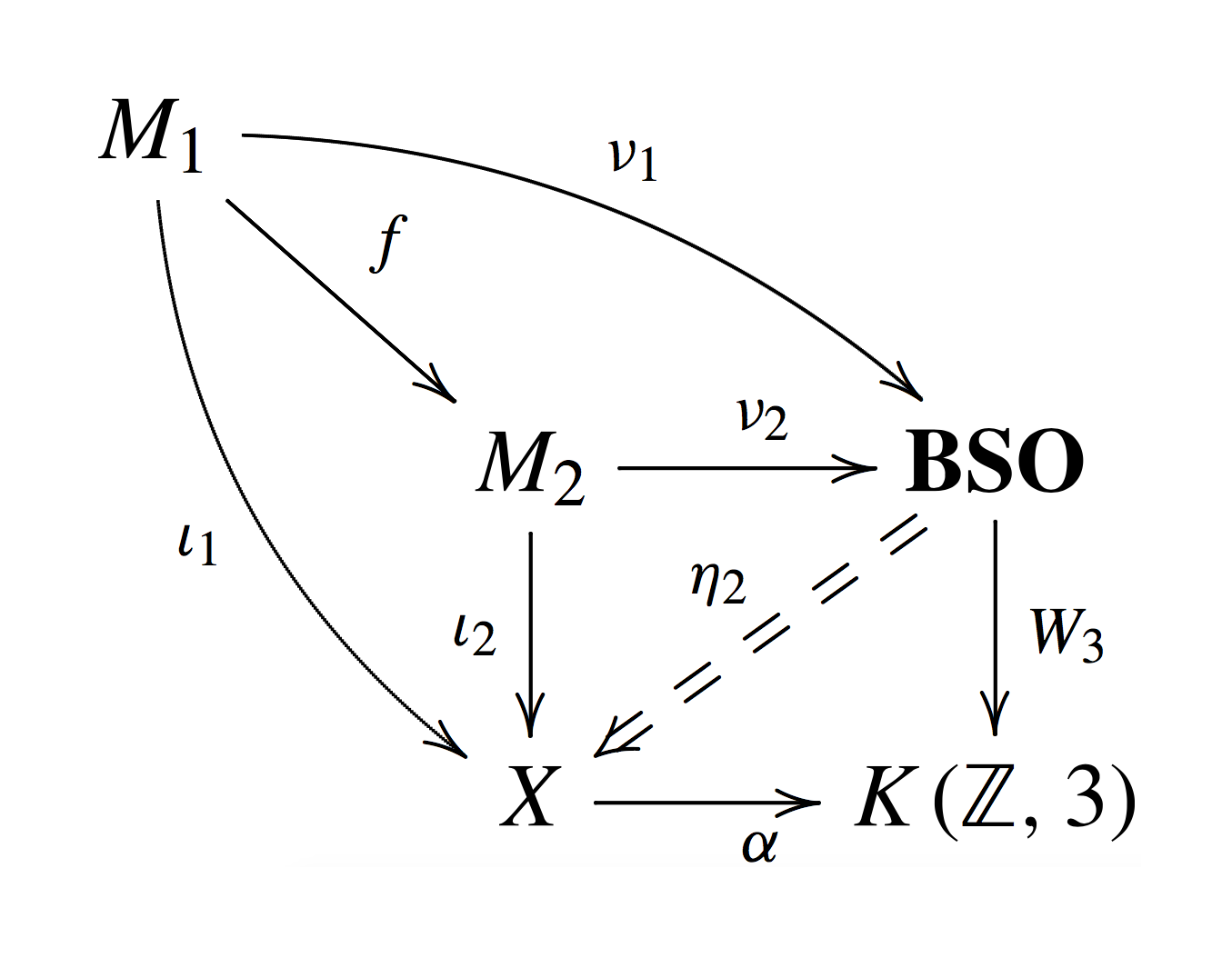
As shown in [e33], this way of thinking about twisted ${Spin}^{c}$ structures generalises to cover higher-degree twists. The latter are important in string topology.

A morphism between $α$ -twisted ${Spin}^{c}$ manifolds $(M_{1}, ν_{1}, ι_{1}, η_{1}) and (M_{2}, ν_{2}, ι_{2}, η_{2})$ is a continuous map $f : M_{1} \to M_{2}$ where the diagram shown to the right is a homotopy commutative diagram such that

$ν_{1}$ is homotopic to $ν_{2} \circ f$ through a continuous map $ν : M_{1} \times [0, 1] \to BSO;$
$ι_{2} \circ f$ is homotopic to $ι_{1}$ through a continuous map $ι : M_{1} \times [0, 1] \to X;$
the composition of homotopies $(α \circ ι) * (η_{2} \circ (f \times id)) * (W_{3} \circ ν)$ is homotopic to $η_{1} .$

Two $α$ -twisted ${Spin}^{c}$ manifolds $(M_{1}, ν_{1}, ι_{1}, η_{1})$ and $(M_{2}, ν_{2}, ι_{2}, η_{2})$ are called isomorphic if there exists a diffeomorphism $f : M_{1} \to M_{2}$ such that the above holds. If the identity map on $M$ induces an isomorphism between $(M, ν_{1},$ $ι_{1}, η_{1})$ and $(M, ν_{2},$ $ι_{2}, η_{2}),$ then these two $α$ -twisted ${Spin}^{c}$ structures are called equivalent.

Orientation reversal in the Grassmannian model defines an involution $r : BSO \to BSO .$ Using this, one may determine a unique equivalence class of $α$ -twisted ${Spin}^{c}$ structures on $- M,$ called the opposite $α$ -twisted ${Spin}^{c}$ structure, simply denoted by $- (M, ν, ι, η) .$

5.1. Bai-Ling Wang’s approach to twisted geometric cycles or BB

I will first review the original approach to twisted geometric cycles and then review the ideas originating with Paul.

Definition: A geometric cycle for $(X, α)$ is a quintuple $(M, ι, ν, η, [E]),$ where $[E]$ is a K-class in $K^{0} (M)$ and $M$ is a smooth closed manifold equipped with an $α$ -twisted ${Spin}^{c}$ structure $(M, ι, ν, η) .$

Two geometric cycles $(M_{1}, ι_{1}, ν_{1}, η_{1}, [E_{1}])$ and $(M_{2}, ι,_{2} ν_{2}, η_{2}, [E_{2}])$ are isomorphic if there is an isomorphism $f : (M_{1}, ι_{1}, ν_{1}, η_{1}) ⟶ (M_{2}, ι_{2}, ν_{2}, η_{2}),$ as $α$ -twisted ${Spin}^{c}$ manifolds over $X,$ such that $f_{!} ([E_{1}]) = [E_{2}] .$

Let $Γ (X, α)$ be the collection of all geometric cycles for $(X, α) .$ We now impose an equivalence relation $\sim$ on $Γ (X, α)$ generated by the following three elementary relations:

Direct sum–disjoint union: If $(M, ι, ν, η, [E_{1}])$ and $(M, ι, ν, η, [E_{2}])$ are two geometric cycles with the same $α$ -twisted ${Spin}^{c}$ structure, then $(M, ι, ν, η, [E_{1}]) \cup (M, ι, ν, η, [E_{2}]) \sim (M, ι, ν, η, [E_{1}] + [E_{2}]) .$
Bordism: Given two geometric cycles $(M_{1}, ι_{1}, ν_{1}, η_{1}, [E_{1}])$ and $(M_{2}, ι_{2},$ $ν_{2},$ $η_{2}, [E_{2}]),$ we call them bordant if there exists an $α$ -twisted ${Spin}^{c}$ manifold $(W, ι, ν, η)$ and $[E] \in K^{0} (W)$ such that $\partial (W, ι, ν, η) = - (M_{1}, ι_{1}, ν_{1}, η_{1}) \cup (M_{2}, ι_{2}, ν_{2}, η_{2})$ and $\partial ([E]) = [E_{1}] \cup [E_{2}] .$ Here $- (M_{1}, ι_{1}, ν_{1}, η_{1})$ denotes the manifold $M_{1}$ with the opposite $α$ -twisted ${Spin}^{c}$ structure.
${Spin}^{c}$ vector bundle modification: Suppose we are given a geometric cycle $(M, ι, ν, η, [E])$ and a ${Spin}^{c}$ vector bundle $V$ over $M$ with even-dimensional fibres. Denote by $\underset{―}{R}$ the trivial rank-1 real vector bundle. Choose a Riemannian metric on $V \oplus \underset{―}{R},$ and let $\hat{M} = S (V \oplus \underset{―}{R})$ be the sphere bundle of $V \oplus \underset{―}{R} .$ Then the vertical tangent bundle $T^{v} (\hat{M})$ of $\hat{M}$ admits a natural ${Spin}^{c}$ structure with an associated $Z_{2}$ -graded spinor bundle $S_{V}^{+} \oplus S_{V}^{-}$ . Denote by $ρ : \hat{M} \to M$ the projection which is K-oriented. Then $(M, ι, ν, η, [E]) \sim (\hat{M}, ι \circ ρ, ν \circ ρ, η \circ ρ, [ρ^{*} E \otimes S_{V}^{+}]) .$

Definition: Denote by $K_{*}^{geo} (X, α) = Γ (X, α) / \sim$ the geometric twisted K-homology. Addition is given by the direct sum - disjoint union relation. Note that the equivalence relation $\sim$ preserves the parity of the dimension of the underlying $α$ -twisted ${Spin}^{c}$ manifold. Now let $K_{0}^{geo} (X, α)$ (resp. $K_{1}^{geo} (X, α)$ ) be the subgroup of $K_{*}^{geo} (X, α)$ determined by all geometric cycles with even-dimensional (resp. odd-dimensional) $α$ -twisted ${Spin}^{c}$ manifolds.

Remark:

If $M,$ in a geometric cycle $(M, ι, ν, η, [E])$ for $(X, α),$ is a compact manifold with boundary, then $[E]$ has to be a class in $K^{0} (M, \partial M) .$
If $f : X \to Y$ is a continuous map and $α : Y \to K (Z, 3)$ is a twisting, then there is a natural homomorphism of abelian groups $f_{*} : K_{ev / odd}^{geo} (X, α \circ f) ⟶ K_{ev / odd}^{geo} (Y, α)$ sending $[M, ι, ν, η, E]$ to $[M, f \circ ι, ν, η, E] .$
Let $A$ be a closed subspace of $X$ and $α$ be a twisting on $X .$ A relative geometric cycle for $(X, A; α)$ is a quintuple $(M, ι, ν, η, [E])$ such that
1. $M$ is a smooth manifold (possibly with boundary), equipped with an $α$ -twisted ${Spin}^{c}$ structure $(M, ι, ν, η);$
2. if $M$ has a nonempty boundary, then $ι (\partial M) \subset A;$
3. $[E]$ is a K-class in $K^{0} (M)$ represented by a $Z_{2}$ -graded vector bundle $E$ over $M,$ or a continuous map $M \to BU (\infty) .$

The relation $\sim$ generated by direct sum - disjoint union, bordism and ${Spin}^{c}$ vector bundle modification is an equivalence relation. The collection of relative geometric cycles, modulo the equivalence relation is denoted by $K_{ev / odd}^{geo} (X, A; α) .$

5.2. $D$ -cycles or AB

The difficulty with the original approach to these twisted geometric cycles outlined in the previous subsection is that it is not clear how to construct them (that is, they do not solve the “general twisted index problem” that we will announce below). A new approach was suggested by Paul and explained in our joint paper [4]. The main difference between this new approach and the approach described earlier in this article is that we make much heavier use of the theory of continuous trace $C^{*}$ -algebras. We emphasise that in this new approach the projective unitary group is equipped with the strong operator topology, not the norm topology as was used in earlier sections.

We begin by recalling a few concepts.

Given an oriented real Euclidean vector bundle $F$ of rank K over a paracompact Hausdorff topological space $Y,$ a ${Spin}^{c}$ structure on $F$ is a lift of the oriented frame bundle $P_{SO} (F)$ to a principal ${Spin}^{c} (k)$ -bundle $P_{{Spin}^{c}} (F),$ where $1 \to U (1) ⟶ {Spin}^{c} (k) ⟶ SO (k) \to 1$ is the unique (for $k > 2$ ) nontrivial central extension of $SO (k)$ by $U (1) .$ See Appendix D in [e11] for an equivalent definition of ${Spin}^{c}$ structures (and note that there is a well-known modification needed for $k \leq 2$ ). A real vector bundle with a ${Spin}^{c}$ structure is called a ${Spin}^{c}$ vector bundle. ${Spin}^{c}$ structures are orientation conditions for complex K-theory in the sense that a ${Spin}^{c}$ vector bundle is a real vector vector bundle with a given complex spinor bundle or a K-theory Thom class. See Section 4 in [3] and Theorem C.12 in [e11] for more discussions of this. In particular, a spinor bundle for $F$ determines an orientation of $F .$
(two-out-of-three principle) Let $0 \to F^{'} ⟶ F ⟶ F^{''} \to 0$ be a short exact sequence of oriented real vector bundles on a paracompact Hausdorff topological space $Y .$ Then ${Spin}^{c}$ structures for any two of the vector bundles determine a ${Spin}^{c}$ structure for the third vector bundle.
A ${Spin}^{c}$ Riemannian manifold is a Riemannian manifold $W$ (perhaps with boundary) whose tangent bundle $T W$ is a ${Spin}^{c}$ vector bundle. If $W$ has a boundary $\partial W,$ at each boundary point, the outward normal vector defines a trivial rank-1 real vector bundle $N_{\partial W}$ over $\partial W$ and $0 \to T (\partial W) ⟶ T W |_{\partial W} ⟶ N_{\partial W} \to 0$ is an exact sequence of real Euclidean vector bundles over $\partial W .$ Therefore, the two-out-of-three principle implies that if a ${Spin}^{c}$ manifold $W$ has a boundary, then this boundary, $\partial W,$ is a ${Spin}^{c}$ manifold in a canonical way.

5.2.1. Twisting data

If $H$ is a complex Hilbert space, $K (H)$ will denote the $C^{*}$ -algebra of all compact operators on $H .$ Hilbert spaces will be assumed to be separable. Recall that a $C^{*}$ -algebra $A$ is an elementary $C^{*}$ -algebra if there exists a complex Hilbert space $H$ and an isomorphism of $C^{*}$ -algebras $A ≅ K (H) .$

Definition: Let $X$ be a second-countable locally compact Hausdorff topological space. A twisting datum on $X$ is a locally trivial bundle $A$ of elementary $C^{*}$ -algebras on $X,$ that is, each fibre of $A$ is an elementary $C^{*}$ -algebra with structure group the automorphism group of $K (H)$ for some complex Hilbert space.

If $E$ is a (locally trivial) bundle of Hilbert spaces on $X,$ then $K (E)$ is the twisting datum defined by $K (E)_{x} = K (E_{x}), x \in X .$ Any twisting datum $A$ is locally of the form $K (E);$ i.e., for any $x \in X$ there exists an open set $U$ in $X$ with $x \in U$ and a (locally trivial) Hilbert space vector bundle $E$ on $U$ with $A | U ≅ K (E) .$

For a $C^{*}$ -algebra $A,$ $A^{op}$ denotes the opposite $C^{*}$ -algebra. As Banach spaces $A = A^{op},$ and $*$ remains unchanged. Thus $a b$ in $A^{op}$ is $b a$ in $A .$ If $A$ is a twisting datum on $X,$ then $A^{op}$ is the twisting datum obtained by replacing each fibre $A_{x}$ by $A_{x}^{op} .$ If $A$ and $B$ are twisting data on $X,$ then $A \otimes B$ is the twisting datum on $X$ whose fibre at $x \in X$ is the $C^{*}$ -algebra $A_{x} \otimes B_{x} .$

Let $A$ be a twisting datum on $X,$ and assume that the fibre of $A$ is infinite-dimensional. As before $P$ denotes the principal $P U (H)$ bundle on $X$ whose fibre at $x \in X$ is $P_{x} = {C^{*} -algebra isomorphisms : K (H) \to A_{x}} .$ There is then the canonical isomorphism of twisting data on $X$ $A ≅ P \times_{U (H)} K (H) .$ Note that the principal $P U (H)$ bundle $P$ is classified by a continuous map $X \to B P U (H) .$ Let $DD (A)$ denote the Dixmier–Douady invariant of $A$ (in $H^{3} (X, Z)$ ).

On the other hand if $A$ has finite-dimensional fibres, we let $B$ be any twisting datum on $X$ with every fibre of $B$ infinite-dimensional and then $DD (A)$ is defined by $DD (A) =: DD (A \otimes B) - DD (B) .$ For any two twisting data $A, B$ on $X$ we have $DD (A \otimes B) = DD (A) + DD (B)$ and $DD (A^{op}) = - DD (A) .$

Definition: A spinor bundle for $A$ is a vector bundle $S$ of Hilbert spaces on $X$ together with a given isomorphism of twisting data $A ≅ K (S) .$ A spinor bundle for $A$ exists if and only if $DD (A) = 0.$

Lemma 8: Let $A$ be any twisting datum on $X .$ Then there is a canonical spinor bundle for $A \otimes A^{op} .$

Proof. The set of Hilbert–Schmidt operators on $H,$ denoted by $L_{H-S} (H),$ is an ideal in $K (H) .$ The $C$ -valued inner product $⟨ T_{1}, T_{2} ⟩ = Trace (T_{1} T_{2}^{*})$ makes $L_{H-S} (H)$ into a Hilbert space. Now let $A$ be an elementary $C^{*}$ -algebra. Choose an isomorphism of $C^{*}$ -algebras $ψ : A \to K (H) .$ Now, $ψ^{- 1} (L_{H-S} (H))$ is an ideal in $A$ and is independent of the choice of $ψ$ because the Hilbert–Schmidt operators are invariant under $Aut (K (H)) = P U (H) .$ Denote this ideal by $A_{H-S} .$ The left-multiplication and right-multiplication actions of $A$ on $A_{H-S}$ combine to give a left action of $A \otimes A^{op}$ on $A_{H-S}$ which identifies $A \otimes A^{op}$ with the compact operators on the Hilbert space $A_{H-S} :$ $A \otimes A^{op} ≅ K (A_{H-S}) .$ If $A$ is a twisting datum on $X,$ let $S$ be the vector bundle of Hilbert spaces on $X$ whose fibre at $x \in X$ is $(A_{x})_{H-S} .$ Then $S$ is a spinor bundle for $A \otimes A^{op}$ and is well-defined as our construction is independent of $ψ .$ ☐

We import our previous notation: if $A$ is a twisting datum on $X,$ then $Γ_{0} (X, A)$ denotes the $C^{*}$ -algebra of all continuous vanishing-at-infinity sections of $A .$ Recall that the compactly supported Kasparov group $K K_{c}^{*} (Γ_{0} (X, A), C)$ is $K K_{c}^{j} (Γ_{0} (X, A), C) := lim_{\begin{matrix} ⟶ \\ Δ \subset X \\ Δ compact \end{matrix}} K K^{j} (Γ (Δ, A), C), j = 0, 1,$ where $Γ (Δ, A)$ is the $C^{*}$ -algebra of all continuous sections of $A$ restricted to $Δ .$ Since $X$ is a CW-complex, this is equal to the direct limit over the finite sub-CW-complexes of $X .$ We will refer to $K K_{c}^{*} (Γ_{0} (X, A), C)$ as the twisted Kasparov K-homology of $X .$

We now expound some elementary results with proofs to give the flavour of the Kasparov theory we used.

Lemma 9: A spinor bundle

S

for

A \otimes B^{op}

determines a stable isomorphism between

Γ_{0} (X, A)

and

Γ_{0} (X, B),

and thus gives an isomorphism

Ψ_{S} : K K_{c}^{j} (Γ_{0} (X, A), C) ≅ K K_{c}^{j} (Γ_{0} (X, B), C), j = 0, 1.

Proof. Let $B_{H-S}$ be the spinor bundle for $B^{op} \otimes B .$ Lemma 8 implies $A \otimes B^{op} \otimes B ≅ A \otimes K (B_{H-S}) .$ If $S$ is a spinor bundle for $A \otimes B^{op},$ then $A \otimes B^{op} \otimes B ≅ K (S) \otimes B .$ Therefore $A \otimes K (B_{H-S}) ≅ K (S) \otimes B .$ Note that the Dixmier–Douady invariants of $K (B_{H-S})$ and $K (S)$ are zero. For any compact subspace $Δ \subset X,$ we have $\begin{array}{lll} K K^{j} (Γ (Δ, A), C) & ≅ & K K^{j} (Γ (Δ, A \otimes K (B_{H-S})), C) \\ ≅ & K K^{j} (Γ (Δ, K (S) \otimes B), C) \\ ≅ & K K^{j} (Γ (Δ, B), C) . \end{array}$ Here the first and the third isomorphisms are provided by Morita equivalence bimodules $B_{H-S}$ and $S$ respectively. Passing to the direct limit, we get the desired isomorphism $Ψ_{S} .$ ☐

5.2.2. K-cycles for twisted K-homology

As above, $X$ is a locally finite CW-complex and $A$ is a twisting datum on $X .$

Definition: A twisted-by- $A$ K-cycle on $X$ is a triple $(M, σ, φ)$ where

$M$ is a compact ${Spin}^{c}$ manifold without boundary,
$φ : M \to X$ is a continuous map,
$σ \in K_{0} (Γ (M, φ^{*} A^{op}))$ (the $K_{0}$ -group of the $C^{*}$ -algebra $Γ (M, φ^{*} A^{op})) .$

Remark: The twisted K-cycles defined here are closely related to the cycles in the original formulation of the Baum–Connes conjecture. Later we will define the notion of $D$ -cycles, motivated by $D$ -branes in string theory, which may be regarded as representing geometric cycles for $(X, A) .$ In fact the two resulting twisted K-homologies are isomorphic.

Keeping $X, A$ fixed, denote by ${(M, φ, σ)}$ the collection of all twisted-by- $A$ K-cycles on $X .$ On this collection impose the equivalence relation $\sim$ generated by the two elementary steps

bordism,
vector bundle modification.

Next, we elaborate on these two steps for the case of twisted K-cycles.

Isomorphism: We say $(M, φ, σ)$ is isomorphic to $(M^{'}, φ^{'}, σ^{'})$ if and only if there exists a diffeomorphism $ψ : M \to M^{'}$ preserving the ${Spin}^{c}$ -structures and with commutativity in the diagram shown to the right and in addition $ψ^{*} (σ^{'}) = σ,$ where $ψ^{*} : K_{0} Γ (M^{'}, φ^{' *} A) ⟶ K_{0} Γ (M, φ^{*} A)$ is the isomorphism of K-theory determined by the isomorphism of $C^{*}$ -algebras $Γ (M^{'}, φ^{' *} A^{op}) ≅ Γ (M, φ^{*} A^{op}) .$

Bordism: We say $(M_{0}, φ_{0}, σ_{0})$ is bordant to $(M_{1}, φ_{1}, σ_{1})$ if and only if there exists $(W, φ, σ)$ such that

$W$ is a compact ${Spin}^{c}$ manifold with boundary;
$φ$ is a continuous map from $W$ to $X;$
$σ \in K_{0} (Γ (W, φ^{*} A^{op}));$
$(\partial W, φ |_{\partial W}, σ |_{\partial W}) ≅ (M_{0}, φ_{0}, σ_{0}) ⊔ (- M_{1}, φ_{1}, σ_{1}) .$

Vector bundle modification: Let $(M, φ, σ)$ be a twisted-by- $A$ K-cycle on $X,$ and let $F$ be a ${Spin}^{c}$ vector bundle on $M$ of even rank. As in the untwisted case, $1_{R}$ denotes the trivial real line bundle on $M,$ $S (F \oplus 1_{R})$ is the unit sphere bundle of $F \oplus 1_{R}$ and $π : S (F \oplus 1_{R}) \to M$ is a fibration. Let $s : M \to S (F \oplus 1_{R})$ be the canonical unit section of $1_{R} .$ Then the given ${Spin}^{c}$ structure for $F$ determines a Gysin homomorphism (see [e32]) $s_{*} : K_{0} (Γ (M, φ^{*} A^{op})) ⟶ K_{0} (Γ (S (F \oplus 1_{R}), (φ \circ π)^{*} A^{op})) .$ Here we use the fact that $s^{*} (φ \circ π)^{*} A^{op} = φ^{*} A^{op} .$ Then $(M, φ, σ) \sim (S (F \oplus 1_{R}), φ \circ π, s_{*} σ) .$ In the following $(S (F \oplus 1_{R}), φ \circ π, s_{*} σ)$ will be denoted by $F # (M, φ, σ)$ and will be referred to as the modification of $(M, φ, σ)$ by $F .$

Composition Lemma: Let $(M, φ, σ)$ be a twisted-by- $A$ K-cycle on $X,$ and let $F$ be an even-rank ${Spin}^{c}$ vector bundle on $M .$ Let $F_{1}$ be an even-rank ${Spin}^{c}$ vector bundle on $S (F \oplus 1_{R}) .$ Then $F_{1} # (F # (M, φ, σ))$ is (in a canonical way) bordant to $(s^{*} F_{1} \oplus F) # (M, φ, σ) .$

Proof. We first construct a bordant manifold $W$ between $S (F_{1} \oplus 1_{R}) and S (s^{*} F_{1} \oplus F \oplus 1_{R}) .$ Let $D (F_{1} \oplus 1_{R})$ be the unit ball bundle of $F_{1} \oplus 1_{R};$ then $S (F_{1} \oplus 1_{R}) = \partial (D (F_{1} \oplus 1_{R}))$ is the underlying manifold for $F_{1} # (F # (M, φ, σ)) .$ Note that $s^{*} F \oplus F \oplus 1_{R}$ is isomorphic to the normal bundle $ν_{ι}$ for the inclusion map $ι : M \to D (F_{1} \oplus 1_{R}),$ where $ι$ is defined by the composition of $s : M \to S (F \oplus 1_{R})$ and the zero section of the bundle $F_{1} \oplus 1_{R}$ over $S (F \oplus 1_{R}) .$ This ensures that we can identify the sphere bundle of $s^{*} F_{1} \oplus F \oplus 1_{R}$ with the boundary of the ball bundle of radius $\frac{1}{4}$ in the normal bundle $ν_{ι} .$ Define $\tilde{W} = D (F_{1} \oplus 1_{R}) - D_{1 / 4} (ν_{ι}) .$ Then $\partial \tilde{W} ≅ S (F_{1} \oplus 1_{R}) ⊔ - S (s^{*} F_{1} \oplus F \oplus 1_{R}) .$ Let $\tilde{φ} : \tilde{W} \subset D (F_{1} \oplus 1_{R}) \overset{π}{\to} S (F \oplus 1_{R}) \overset{π_{F}}{\to} M$ be the obvious projection and $\tilde{s}$ be the composition of the canonical unit sections $s$ and $s_{1}$ for $F \oplus 1_{R}$ and $F_{1} \oplus 1_{R}$ respectively. Then $(\tilde{W}, \tilde{φ}, {\tilde{s}}_{*} σ)$ provides the bordism between $F_{1} # (F # (M, φ, σ))$ and $(s^{*} F_{1} \oplus F) # (M, φ, σ) .$ Here we applied the facts that the pushforward map ${\tilde{s}}_{*}$ is functorial and is also a homotopy invariant. ☐

Two twisted-by- $A$ K-cycles $(M, φ, σ)$ and $(M^{'}, φ^{'}, σ^{'})$ on $X$ are equivalent if and only if it is possible to pass from $(M, φ, σ)$ to $(M^{'}, φ^{'}, σ^{'})$ by a finite sequence of the two elementary steps. The K-cycle (or topological) twisted-by- $A$ K-homology of $X,$ denoted by $K_{*}^{top} (X, A),$ is the set of equivalence classes of twisted-by- $A$ K-cycles: $K_{*}^{top} (X, A) := {(M, φ, σ)} / \sim .$ Addition in $K_{*}^{top} (X, A)$ is defined by disjoint union of twisted-by- $A$ K-cycles: $(M, φ, σ) + (M^{'}, φ^{'}, σ^{'}) = (M ⊔ M^{'}, φ ⊔ φ^{'}, σ \oplus σ^{'}) .$

Definition: Let $(M, φ, σ)$ be a twisted-by- $A$ K-cycle on $X .$ We say $(M, φ, σ)$ bounds if and only if there exists $(W, \tilde{φ}, \tilde{σ}),$ where

$W$ is a compact ${Spin}^{c}$ manifold with boundary,
$\tilde{φ} : W \to X$ is a continuous map,
$\tilde{σ} \in K_{0} (Γ (W, {\tilde{φ}}^{*} A^{op})),$
$(\partial W, \tilde{φ} |_{\partial W}, \tilde{σ} |_{\partial W}) ≅ (M, φ, σ) .$

As in the untwisted case, the additive inverse of $(M, φ, σ)$ is $(- M, φ, σ) .$ The equivalence relation $\sim$ on twisted-by- $A$ K-cycles $(M, φ, σ)$ preserves the dimension of $M$ modulo 2. Therefore, as an abelian group, $K_{*}^{top} (X, A)$ is the direct sum $K_{*}^{top} (X, A) = K_{0}^{top} (X, A) \oplus K_{1}^{top} (X, A),$ where $K_{j}^{top} (X, A)$ is the subgroup of $K_{*}^{top} (X, A)$ generated by those twisted-by- $A$ K-cycles $(M, φ, σ)$ such that every connected component of $M$ has dimension $\equiv j modulo 2,$ $j = 0, 1.$

There is a natural map $η_{X} : K_{j}^{top} (X, A) ⟶ K K_{c}^{j} (Γ_{0} (X, A), C)$ defined as follows. Given a twisted-by- $A$ K-cycle $(M, φ, σ)$ on $X,$ by applying Poincaré duality in twisted K-theory (see [e31] and [e35]) $K K_{0} (C, Γ (M, φ^{*} A^{op})) ≅ K K^{j} (Γ (M, φ^{*} A), C),$ we have $P D (σ) \in K K^{j} (Γ (M, φ^{*} A), C) .$ Denote by $φ_{*} : K K^{*} (Γ (M, φ^{*} A), C) ⟶ K K_{c}^{*} (Γ_{0} (X, A), C)$ the map of abelian groups induced by $φ : M \to X .$ Then the natural map $η_{X}$ is given by $η_{X} (M, φ, σ) = φ_{*} (P D (σ)) .$ It is routine to check that $η_{X}$ is well-defined on $K_{j}^{top} (X, A)$ and is functorial in the following sense. Let $f : Y \to X$ be a continuous map and $X$ be equipped with a twisting datum $A;$ then the following diagram commutes: $\begin{matrix} K_{j}^{top} (Y, f^{*} A) & \to_{}^{f_{*}} & K_{j}^{top} (X, A) \\ ↓ η_{Y} & ↓ η_{X} \\ K K_{c}^{j} (Γ_{0} (Y, f^{*} A), C) & \to_{}^{f_{*}} & K K_{c}^{j} (Γ_{0} (X, A), C) . \end{matrix}$ Here $f_{*} : K_{j}^{top} (Y, f^{*} A) ⟶ K_{j}^{top} (X, A)$ is defined by $(M, φ, σ) ⟼ (M, f \circ φ, σ)$ on the level of K-cycles.

Paul has often enunciated the untwisted version of the following problem.

The General Twisted Index Problem: When $X$ is a locally finite CW-complex and $A$ is a twisting datum on $X$ then the general twisted index problem is: given an element $ξ \in K K_{c}^{*} (Γ_{0} (X, A), C),$ explicitly construct a twisted-by- $A$ K-cycle $(M, φ, σ)$ for $(X, A)$ with $η (M, φ, σ) = ξ .$

The issue in this problem is constructibility of the K-cycle.

In [4] the following is proved using the notion of normal bordism (introduced next) to establish the six-term exact sequence in Kasparov K-homology of $X .$

Theorem 10: Let $X$ be a locally finite CW-complex with a given twisting datum $A .$ Then the natural map $η_{X} : K_{j}^{top} (X, A) ⟶ K K_{c}^{j} (Γ_{0} (X, A), C), j = 0, 1,$ is an isomorphism of abelian groups.

5.2.3. Normal bordism

One of the main innovations in [4] was the elucidation of the fundamental role of normal bordism. Let $(M, φ, σ)$ be a twisted-by- $A$ K-cycle on $X .$ A normal bundle for $M$ is an real vector bundle $ν$ on $M$ together with a given short exact sequence $0 \to T M ⟶ M \times R^{q} ⟶ ν \to 0$ of real vector bundles on $M .$ Here $q$ is a positive integer and $M \times R^{q}$ is the trivial real vector bundle with fibre $R^{q} .$ The two-out-of-three principle implies that $ν$ is a ${Spin}^{c}$ vector bundle. If $ν$ has even-dimensional fibres, then the modification of $(M, φ, σ)$ by $ν$ will be denoted by $ν # (M, φ, σ) .$

Definition: Two twisted-by- $A$ K-cycles $(M, φ, σ)$ and $(M^{'}, φ^{'}, σ^{'})$ are normally bordant, denoted by $(M, φ, σ) \sim_{N} (M^{'}, φ^{'}, σ^{'}),$ if there exist normal bundles with even-dimensional fibres $ν$ and $ν^{'}$ for $M$ and $M^{'}$ respectively such that $ν # (M, φ, σ)$ is bordant to $ν^{'} # (M^{'}, φ^{'}, σ^{'}) .$

Lemma 11: Normal bordism is an equivalence relation.

Remark: The content of the next lemma is that for normal bordism there is no need to use elementary steps etc. The idea of normal bordism was first constructed by Jakob in [e22] for an alternative definition of generalised homology theory, and further applied in [e28] and [e38] in the study of various versions of geometric K-homology.

Lemma 12: Two twisted-by- $A$ K-cycles $(M, φ, σ)$ and $(M^{'}, φ^{'}, σ^{'})$ are equivalent if and only if they are normally bordant.

A twisted-by- $A$ K-cycle $(M, φ, σ)$ is zero in $K_{*}^{top} (X, A)$ if and only if $(M, φ, σ)$ is normally bordant to a twisted-by- $A$ K-cycle which bounds.

5.2.4. The group of $D$ -cycles

In this section, we introduce another notion of K-cycles for $(X, A),$ called $D$ -cycles, which are closely related to the notion of $D$ -branes in string theory. We begin with the following:

Definition: A $D$ -cycle for $(X, A)$ is a 4-tuple $(M, E, φ, S)$ such that

$M$ is a closed oriented $C^{\infty}$ Riemannian manifold;
$E$ is a complex vector bundle on $M;$
$φ$ is a continuous map from $M$ to $X;$
$S$ is a spinor bundle for ${Cliff}_{C}^{+} (T M) \otimes φ^{*} A^{op} .$

Remark:

If $M$ is even-dimensional, then ${Cliff}_{C}^{+} (T M)$ is the twisting datum on $M$ whose fibre at $p \in M$ is the complexified Clifford algebra $C \otimes_{R} Cliff (T_{p} M) .$ As usual, $T_{p} M$ is the tangent space to $M$ at $p .$ On the other hand, if $M$ is odd-dimensional, given $p \in M,$ choose a positively oriented orthonormal basis $e_{1}, e_{2}, \dots, e_{n}$ for $T_{p} M .$ Set $n = 2 r + 1$ and define $ω (p) \in C \otimes_{R} Cliff (T_{p} M)$ by $ω (p) = i^{r + 1} e_{1} e_{2} \dots e_{n} .$ Then $ω (p)$ does not depend on the choice of positively oriented orthonormal basis for $T_{p} M .$ Also $ω (p)$ is in the centre of ${Cliff}_{C} (T_{p} M) = C \otimes_{R} Cliff (T_{p} M)$ and $ω (p)^{2} = 1.$
Now set ${Cliff}_{C}^{+} (T_{p} M) = {a \in {Cliff}_{C} (T_{p} M) ∣ ω (p) a = a} .$ Then ${Cliff}_{C}^{+} (T M)$ is the twisting datum on $M$ whose fibre at $p \in M$ is ${Cliff}_{C}^{+} (T_{p} M) .$
The existence of a spinor bundle $S$ for ${Cliff}_{C}^{+} (T M) \otimes φ^{*} A^{op}$ implies $DD ({Cliff}_{C}^{+} (T M)) = φ^{*} (DD (A)) .$ By standard algebraic topology, $DD ({Cliff}_{C}^{+} (T M))$ is the third (integral) Stiefel–Whitney class of $M,$ so the existence of $S$ implies $W_{3} (M) = φ^{*} (DD (A)),$ which is the Freed–Witten anomaly cancellation condition for Type IIB $D$ -branes as explained in [e33].

Definition: Keeping $(X, A)$ fixed, denote by ${(M, E, φ, S)}$ the collection of all $D$ -cycles for $(X, A) .$ On this collection impose the equivalence relation $\sim$ generated by the three elementary steps

bordism,
direct sum - disjoint union,
vector bundle modification.

These three elementary moves can be precisely defined as follows.

Isomorphism: Two $D$ -cycles $(M, E, φ, S),$ $(M^{'}, E^{'}, φ^{'}, S^{'})$ for $(X, A)$ are isomorphic if there is an orientation-preserving isometric diffeomorphism $f : M \to M^{'}$ such that the diagram shown to the right commutes, and $f^{*} E^{'} ≅ E,$ $f^{*} S^{'} ≅ S .$

Bordism: Two $D$ -cycles $(M_{0}, E_{0}, φ_{0}, S_{0}),$ $(M_{1}, E_{1}, φ_{1}, S_{1})$ for $(X, A)$ are bordant if there exists a 4-tuple $(W, E, Φ, S)$ such that $W$ is a compact oriented Riemannian manifold with boundary, $E$ is a complex vector bundle on $W,$ $Φ$ is a continuous map from $W \to X$ and $(\partial W, E | \partial W, Φ | \partial W, S^{(+)} | \partial W) ≅ (M_{0}, E_{0}, φ_{0}, S_{0}) ⊔ (- M_{1}, E_{1}, φ_{1}, S_{1}) .$ When $W$ is of odd dimension, ${Cliff}_{C}^{(+)} (T W) | \partial W ≅ {Cliff}_{C} (T (\partial W) .$ Then $S^{(+)} = S .$ When $W$ is of even dimension, $S^{(+)}$ is the positive part of $S,$ the $(+ 1)$ -eigenbundle of the chirality section of ${Cliff}_{C}^{(+)} (T W) .$

Direct sum-disjoint union: Let $(M, E, φ, S)$ be a $D$ -cycle for $(X, A)$ and let $E^{'}$ be a complex vector bundle on $M;$ then $(M, E, φ, S) ⊔ (M, E^{'}, φ, S) \sim (M, E \oplus E^{'}, φ, S) .$

Vector bundle modification: Let $(M, E, φ, S)$ be a $D$ -cycle for $(X, A)$ and let $F$ be a ${Spin}^{c}$ vector bundle on $M$ with even-dimensional fibres. Then, with $S_{F}$ being the Spinor bundle for the ${Spin}^{c}$ vector bundle $F,$ $(M, E, φ, S) \sim (S (F \oplus 1_{R}), β \otimes π^{*} E, φ \circ π, π^{*} S_{F} \otimes π^{*} S),$ with the other notation in this equivalence being the same as that introduced previously. The group of $D$ -cycles for $(X, A),$ denoted by $K_{*}^{geo} (X, A),$ is the set of equivalence classes of these $D$ -cycles under the equivalence defined above in terms of the three relations. Addition in $K_{*}^{geo} (X, A)$ is disjoint union of $D$ -cycles: $(M, E, φ, S) + (M^{'}, E^{'}, φ^{'}, S^{'}) = (M ⊔ M^{'}, E ⊔ E^{'}, φ ⊔ φ^{'}, S ⊔ S^{'}) .$ The equivalence relation $\sim$ on $D$ -cycles $(M, E, φ, S)$ preserves the dimension of $M$ modulo 2 so that we have $K_{*}^{geo} (X, A) = K_{0}^{geo} (X, A) \oplus K_{1}^{geo} (X, A),$ where $K_{j}^{geo} (X, A)$ is the subgroup of $K_{*}^{geo} (X, A)$ generated by those $(X, A)$ $D$ -cycles $(M, E, φ, S)$ such that every connected component of $M$ has dimension $\equiv j$ modulo 2, $j = 0, 1.$

Let $(M, E, φ, S)$ be a $D$ -cycle on $(X, A)$ such that every connected component of $M$ has its dimension congruent to $j$ modulo $2.$ Let $D_{E}$ denote the Dirac element of $M$ tensored with $E .$ It can be described in terms of the $\frac{1}{2}$ -signature operator on $M .$ Then as in [e8], $D_{E}$ yields an element in the Kasparov K-homology group $[D_{E}] \in K K^{j} (C (M, {Cliff}_{C}^{(+)} (M)), C) .$ The isomorphism $Ψ_{S}$ defined in Lemma 9 in Section 5 reads as $Ψ : K K^{j} (C (M, {Cliff}_{C}^{(+)} (M)), C) ⟶ K K^{j} (Γ (M, φ^{*} A), C) .$ The map of $C^{*}$ -algebras $Γ (X, A) \to Γ (M, φ^{*} A)$ induces a homomorphism of abelian groups $φ_{*} : K K^{j} (Γ (M, φ^{*} A), C) ⟶ K K^{j} (Γ (X, A), C) .$ Then $(M, E, φ, S) \mapsto φ_{*} [D_{E}]$ yields a homomorphism of abelian groups, denoted by $μ : K_{*}^{geo} (X, A) ⟶ K K^{*} (Γ (X, A), C) .$ We call this the twisted index map in twisted K-homology of $(X, A) .$

5.2.5. The charge map $K_{}^{geo} (X, A) \to K_{}^{top} (X, A)$

We use normal bundle modification to define a homomorphism of abelian groups

h : K_{*}^{geo} (X, A) ⟶ K_{*}^{top} (X, A) .

Here

h

should be viewed as the map which sends a

D

-cycle

(M, E, φ, S)

to its charge.

Definition: Given a $D$ -cycle $(M, E, φ, S)$ choose a normal bundle $ν$ for $M,$ with even-dimensional fibres. Then $h (M, E, φ, S) := ν # (M, E, φ, S) = (S (ν \oplus 1_{R}), φ \circ π, σ) .$ Note that $S (ν \oplus 1_{R})$ is a ${Spin}^{c}$ manifold because its tangent bundle is stably trivialized. Here $σ$ is the element in $K_{0} (Γ (S (ν \oplus 1_{R}, (φ \circ π)^{*} A^{op}))$ obtained from $E$ as follows:

Denote by $s_{*} : K^{0} (M) ⟶ K_{0} (Γ (S (ν \oplus 1_{R}), π^{*} {Cliff}_{C} (ν)))$ the Gysin homomorphism associated to the canonical section $s : M \to S (ν \oplus 1_{R}) .$
Observe that, as twisting data on $M,$ a trivialisation of $T M \oplus ν$ gives an equivalence ${Cliff}_{C}^{+} (T M) \otimes φ^{*} A^{op} \sim {Cliff}_{C} (ν)^{op} \otimes φ^{*} A^{op},$ a stable isomorphism of bundles of elementary $C^{*}$ -algebras. Hence the given spinor bundle $S$ for ${Cliff}_{C}^{+} (T M) \otimes φ^{*} A^{op}$ determines a spinor bundle $\tilde{S}$ for ${Cliff}_{C} (ν)^{op} \otimes φ^{*} A^{op} .$ Then $π^{*} \tilde{S}$ is a spinor bundle for $π^{*} {Cliff}_{C} (ν)^{op} \otimes (φ \circ π)^{*} A^{op}$ and therefore yields an isomorphism of abelian groups $χ : K_{0} (Γ (S (ν \oplus 1_{R}), π^{*} {Cliff}_{C} (ν))) ⟶ K_{0} (Γ (S (ν \oplus 1_{R}), (φ \circ π)^{*} A^{op})) .$
$σ := χ (s_{*} [E]) .$

Question: Is the map $h : K_{j}^{geo} (X, A) ⟶ K_{j}^{top} (X, A)$ an isomorphism for any locally finite CW-complex?

Given a positive answer to this question then we would have the following corollary:

Consequence: Let $X$ be a locally finite CW-complex with a twisting datum $A$ defined by a principal $PU (H)$ -bundle $P,$ and $K_{*}^{geo} (X, P)$ be the twisted geometric K-homology of $(X, P)$ in [e33]. Then the twisted index map $μ : K_{*}^{geo} (X, P) ⟶ K K_{c}^{*} (Γ (X, A), C)$ is an isomorphism.

6. The latest chapter in the story

The authors of [4] have, both separately and in collaboration, come up with various proposals for answering the question posed above but a complete argument eluded us. Recently Paul and collaborators [5] answered the question in the affirmative, thus explaining how the original ideas of Bai-Ling Wang, in understanding the Freed–Witten anomaly cancellation condition, form the key assumption for creating twisted geometric cycles.

Moreover this very latest proof is the most general so far. It allows by one method to establish all previous versions of the general index problem in both the twisted and untwisted cases.

In this new argument Wang’s appeal to a twisted version of the Conner–Floyd splitting theorem is replaced by a twisted analogue of a theorem of Hopkins and Hovey. They proved that ${Spin}^{c}$ -bordism of a CW-complex determines its K-homology by a simple algebraic tensor product. That is, the affirmative answer to the question posed above that is established in [5] rests on a twisted version of this theorem of Hopkins and Hovey.

Recall that given a CW-complex $X$ with a twisting $α : X \to K (Z, 3),$ there are two approaches to define to twisted ${Spin}^{c}$ -bordism theory of $(X, α)$ in [e33]. The first approach is the geometric definition using a smooth manifold $M$ with a continuous map $ι : M \to X$ and a homotopy realising the Freed–Witten condition (see [e19]) $\begin{matrix} (5) & ι^{*} ([α]) + W_{3} (M) = 0, \end{matrix}$ where $W_{3} (M)$ is the third integral Stiefel–Whitney class of $M$ and $[α]$ denotes the homotopy class of $α$ in $[X, K (Z, 3)] ≅ H^{3} (X, Z) .$ The $α$ -twisted ${Spin}^{c}$ -bordism group of $X,$ denoted by $Ω_{*}^{{Spin}^{c}} (X, α),$ is defined to be the set of all isomorphism classes of closed $α$ -twisted ${Spin}^{c}$ manifolds over $X$ modulo null-bordism, with the sum given by the disjoint union. The twisted Hopkins–Hovey theorem in [5] gives a precise relationship between this former group and the $D$ -cycle model for twisted K-homology.

This result is the key to proving that the geometric model for twisted K-homology in terms of $D$ -cycles, (studied in one form by Bai-Ling Wang and reformulated by us as explained in [4]) is in fact isomorphic to Kasparov’s analytic twisted K-homology. Moreover these $D$ -cycles are a mathematical version of the physicists’ $D$ -branes.

The upshot for the present essay is that all of the models for the group of twisted K-homology classes discussed previously are isomorphic. I will not discuss the details of [5] here. Paul is preparing an expository account which will provide a useful overview.

References

[e1] J. Dixmier and A. Douady: “Champs continus d’espaces hilbertiens et de $C^{*}$ -algèbres,” Bull. Soc. Math. France 91 (1963), pp. 227–284. MR 163182 Zbl 0127.33102 article

[e2] N. H. Kuiper: “The homotopy type of the unitary group of Hilbert space,” Topology 3 (1965), pp. 19–30. MR 179792 Zbl 0129.38901 article

[e3] A. Grothendieck: “Le groupe de Brauer, I: Algèbres d’Azumaya et interprétations diverses,” pp. 199–219 in Séminaire Bourbaki, vol. 9, Exp. No. 290. Soc. Math. France (Paris), 1964–1966. Reprinted as pp. 46–66 in Dix exposés sur la cohomologie des schémas, Adv. Stud. Pure Math. 3, North-Holland, Amsterdam, 1968. Zbl 0186.54702 incollection

[e4] P. Donovan and M. Karoubi: “Graded Brauer groups and $K$ -theory with local coefficients,” Inst. Hautes Études Sci. Publ. Math. 38 (1970), pp. 5–25. MR 282363 Zbl 0207.22003 article

[e5] J. Giraud: Cohomologie non abélienne. Die Grundlehren der mathematischen Wissenschaften 179. Springer, 1971. MR 344253 Zbl 0226.14011 book

[e6] G. G. Kasparov: “Topological invariants of elliptic operators, I: $K$ -homology,” Izv. Akad. Nauk SSSR Ser. Mat. 39 : 4 (1975), pp. 796–838. In Russian; translated in Math USSR-Izv. 9:4 (1975), 751–792. MR 488027 Zbl 0337.58006 article

[e7] P. E. Conner: Differentiable periodic maps, 2nd edition. Lecture Notes in Mathematics 738. Springer, 1979. MR 548463 Zbl 0417.57019 book

[e8] G. G. Kasparov: “The operator $K$ -functor and extensions of $C^{*}$ -algebras,” Izv. Akad. Nauk SSSR Ser. Mat. 44 : 3 (1980), pp. 571–636. In Russian; translated in Math. USSR-Izv. 15:3 (1981), 513–572. MR 582160 Zbl 0448.46051 article

[e9] G. G. Kasparov: “Equivariant $K K$ -theory and the Novikov conjecture,” Invent. Math. 91 : 1 (1988), pp. 147–201. MR 918241 Zbl 0647.46053 article

[e10] J. Rosenberg: “Continuous-trace algebras from the bundle theoretic point of view,” J. Austral. Math. Soc. Ser. A 47 : 3 (1989), pp. 368–381. MR 1018964 Zbl 0695.46031 article

[e11] H. B. Lawson, Jr. and M.-L. Michelsohn: Spin geometry. Princeton Mathematical Series 38. Princeton University Press, 1989. MR 1031992 Zbl 0688.57001 book

[e12] N. Berline, E. Getzler, and M. Vergne: Heat kernels and Dirac operators. Grundlehren der Mathematischen Wissenschaften 298. Springer, 1992. MR 1215720 Zbl 0744.58001 book

[e13] J.-L. Brylinski: Loop spaces, characteristic classes and geometric quantization. Progress in Mathematics 107. Birkhäuser (Boston), 1993. MR 1197353 Zbl 0823.55002 book

[e14] J. Polchinski: “Dirichlet branes and Ramond–Ramond charges,” Phys. Rev. Lett. 75 : 26 (1995), pp. 4724–4727. MR 1366179 Zbl 1020.81797 article

[e15] M. K. Murray: “Bundle gerbes,” J. London Math. Soc. (2) 54 : 2 (1996), pp. 403–416. MR 1405064 Zbl 0867.55019 article

[e16] R. Minasian and G. Moore: “ $K$ -theory and Ramond–Ramond charge,” J. High Energy Phys. 11 (1997), pp. Paper~2. MR 1606278 Zbl 0949.81511 article

[e17] I. Raeburn and D. P. Williams: Morita equivalence and continuous-trace $C^{*}$ -algebras. Mathematical Surveys and Monographs 60. Amer. Math. Soc. (Providence, RI), 1998. MR 1634408 Zbl 0922.46050 book

[e18] E. Witten: “D-branes and $K$ -theory,” J. High Energy Phys. 12 (1998), pp. Paper~19. MR 1674715 Zbl 0959.81070 article

[e19] D. S. Freed and E. Witten: “Anomalies in string theory with D-branes,” Asian J. Math. 3 : 4 (1999), pp. 819–851. MR 1797580 Zbl 1028.81052 article

[e20] P. Bouwknegt and V. Mathai: “D-branes, $B$ -fields and twisted $K$ -theory,” J. High Energy Phys. 3 (2000), pp. Paper~7. MR 1756434 Zbl 0959.81037 article

[e21] D. S. Freed and M. Hopkins: “On Ramond–Ramond fields and $K$ -theory,” J. High Energy Phys. 5 (2000), pp. Paper~44. MR 1769477 Zbl 0990.81624 article

[e22] M. Jakob: “An alternative approach to homology,” pp. 87–97 in Une dégustation topologique [Topological morsels]: homotopy theory in the Swiss Alps (Arolla, 1999). Edited by D. Arlettaz and K. Hess. Contemp. Math. 265. Amer. Math. Soc. (Providence, RI), 2000. MR 1803953 Zbl 0971.55008 incollection

[e23] A. Kapustin: “D-branes in a topologically nontrivial $B$ -field,” Adv. Theor. Math. Phys. 4 : 1 (2000), pp. 127–154. MR 1807598 Zbl 0992.81059 article

[e24] P. Bouwknegt, A. L. Carey, V. Mathai, M. K. Murray, and D. Stevenson: “Twisted $K$ -theory and $K$ -theory of bundle gerbes,” Comm. Math. Phys. 228 : 1 (2002), pp. 17–45. MR 1911247 Zbl 1036.19005 article

[e25] V. Mathai, M. K. Murray, and D. Stevenson: “Type-I D-branes in an $H$ -flux and twisted $K O$ -theory,” J. High Energy Phys. 11 (2003), pp. art.~id.~053. MR 2039437 article

[e26] M. K. Murray and M. A. Singer: “Gerbes, Clifford modules and the index theorem,” Ann. Global Anal. Geom. 26 : 4 (2004), pp. 355–367. MR 2103405 Zbl 1107.19003 article

[e27]M. Atiyah and G. Segal: “Twisted $K$ -theory,” Ukr. Mat. Visn. 1 : 3 (2004), pp. 287–330. MR 2172633 Zbl 1151.55301 article

[e28] J. Raven: An equivariant bivariant Chern character. Ph.D. thesis, The Pennsylvania State University, 2004. MR 2706816 phdthesis

[e29] R. M. G. Reis and R. J. Szabo: “Geometric $K$ -homology of flat D-branes,” Comm. Math. Phys. 266 : 1 (2006), pp. 71–122. MR 2231967 Zbl 1107.58016 article

[e30] J. Brodzki, V. Mathai, J. Rosenberg, and R. J. Szabo: “D-branes, RR-fields and duality on noncommutative manifolds,” Comm. Math. Phys. 277 : 3 (2008), pp. 643–706. MR 2365448 Zbl 1162.58008 article

[e31] S. Echterhoff, H. Emerson, and H. J. Kim: “ $K K$ -theoretic duality for proper twisted actions,” Math. Ann. 340 : 4 (2008), pp. 839–873. MR 2372740 Zbl 1147.19006 article

[e32] A. L. Carey and B.-L. Wang: “Thom isomorphism and push-forward map in twisted $K$ -theory,” J. K-Theory 1 : 2 (2008), pp. 357–393. MR 2434190 Zbl 1204.55006 article

[e33] B.-L. Wang: “Geometric cycles, index theory and twisted $K$ -homology,” J. Noncommut. Geom. 2 : 4 (2008), pp. 497–552. MR 2438341 Zbl 1169.19003 article

[e34] R. J. Szabo: D-branes and bivariant K-theory. Preprint, 2008. ArXiv 0809.3029 techreport

[e35] J.-L. Tu: “Twisted $K$ -theory and Poincaré duality,” Trans. Amer. Math. Soc. 361 : 3 (2009), pp. 1269–1278. MR 2457398 Zbl 1173.46052 article

[e36] R. M. G. Reis, R. J. Szabo, and A. Valentino: “KO-homology and type I string theory,” Rev. Math. Phys. 21 : 9 (2009), pp. 1091–1143. MR 2573141 Zbl 1180.81117 article

[e37] A. L. Carey and B.-L. Wang: “Riemann–Roch and index formulae in twisted $K$ -theory,” pp. 95–131 in Superstrings, geometry, topology, and $C^{*}$ -algebras (Fort Worth, TX, 2009). Edited by R. S. Doran, G. Friedman, and J. Rosenberg. Proc. Sympos. Pure Math. 81. Amer. Math. Soc. (Providence, RI), 2010. MR 2681760 Zbl 1210.81080 incollection

[e38] R. J. Deeley: “Geometric $K$ -homology with coefficients I: $Z / k Z$ -cycles and Bockstein sequence,” J. K-Theory 9 : 3 (2012), pp. 537–564. MR 2955974 Zbl 1256.19005 article

Works

[1] P. Baum and R. G. Douglas: “Index theory, bordism, and $K$ -homology,” pp. 1–31 in Operator algebras and $K$ -theory (San Francisco, 7–8 January 1981). Edited by R. G. Douglas and C. Schochet. Contemporary Mathematics 10. American Mathematical Society (Providence, RI), 1982. MR 658506 Zbl 0507.55004 incollection

Our purpose in this note is threefold. After giving brief and selective descriptions of the topological and analytical realizations of $ K $-homology, we present our view of index theory. Sedond, we shall say more about our proof of the isomorphism of topological and analytical realizations of $ K $-homology since that lies at the heart of matters. In particular, we want to discuss the bordism step of the proof since this makes contact with a number of interesting topics including relative $ K $-homology and elliptic boundary value problems. Lastly, we want to work out a key step in the bordism proof in two special cases where the result may have independent interest.

Claude L. Schochet	Related
Ronald George Douglas	Related

[2] P. Baum and R. G. Douglas: “ $K$ homology and index theory,” pp. 117–173 in Operator algebras and applications (Kingston, ON, 14 July–2 August 1980), part 1. Edited by R. V. Kadison. Proceedings of Symposia in Pure Mathematics 38. American Mathematical Society (Providence, RI), 1982. MR 679698 Zbl 0532.55004 incollection

Ronald George Douglas	Related
Richard V. Kadison	Related

[3] P. Baum, N. Higson, and T. Schick: “On the equivalence of geometric and analytic $K$ -homology,” pp. 1–24 in Special issue: In honor of Robert D. MacPherson, Part 3, published as Pure Appl. Math. Q. 3 : 1. International Press (Sommerville, MA), 2007. MR 2330153 Zbl 1146.19004 incollection

Thomas Schick	Related
Nigel David Higson	Related
Robert Duncan MacPherson	Related

[4] P. Baum, A. Carey, and B.-L. Wang: “ $K$ -cycles for twisted $K$ -homology,” pp. 69–98 in Nanjing special issue on K-theory, number theory and geometry, published as J. K-Theory 12 : 1. Issue edited by X. Guo, H. Qin, and G. Tang. Cambridge University Press, August 2013. MR 3126635 Zbl 1300.19003 incollection

Hourong Qin	Related
Bai-Ling Wang	Related
Alan Lawrence Carey	Related
Guoping Tang	Related
Xuejun Guo	Related

[5] P. Baum, M. Joachim, M. Khorami, and T. Schick: Twisted $s p i n^{c}$ -bordism, D-branes, and twisted K-homology. In preparation. techreport

Thomas Schick	Related
Michael Joachim	Related
Mehdi Khorami	Related