by Joe Buhler
Research often feels like play to mathematicians, and Elwyn Berlekamp exemplified this in many different ways. Anyone who talked to him about information theory, algorithms, probability, codes, finance, and signal processing certainly saw this twinkle-in-the-eye spirit in his joy, love of cleverness and novelty, and occasional hints of competitiveness.
All of this was greatly amplified whenever games or puzzles were the actual subject! His work on combinatorial games (with John Conway and Richard Guy) [1], [2] covered a vast array of games and puzzles, and included deep dives into the underlying mathematics that emerged.1 Elwyn (and David Wolfe) applied this body of work to endgames in the game of Go [3] (preceding AlphaGo by 20 years in doing better than the best professional players in an aspect of this notoriously deep game). Later, partially motivated by ideas from economics, he introduced the general idea of “coupon collecting,” which forces players to assess the value of currently being on move.
It would be possible to expound at length on any of the above, or on his many other activities — philanthropy, service on the boards of national science societies, financial companies (e.g., with Jim Simons), support for MSRI over the years, support for STEM education and recreational mathematics, etc. However, here I will just focus on my own experiences with Elwyn, prefaced by some remarks on juggling. We each (separately) spent time honing the sort of physical cleverness required to become good at this skill, and the insight it gave me into Elwyn’s personality was borne out in the subsequent years of our work together in connection with MSRI.
Before I met him in Berkeley in the early 1980s, I knew that Berlekamp had written a highly regarded book on error-correcting codes, and that he was writing a multivolume tome on combinatorial games with Conway and Guy. I had also learned (from Ron Graham) something truly remarkable, which speaks to Elwyn’s core traits. Namely, he mastered the reverse five-ball cascade juggling pattern before learning the more normal (“inside”) five-ball cascade.
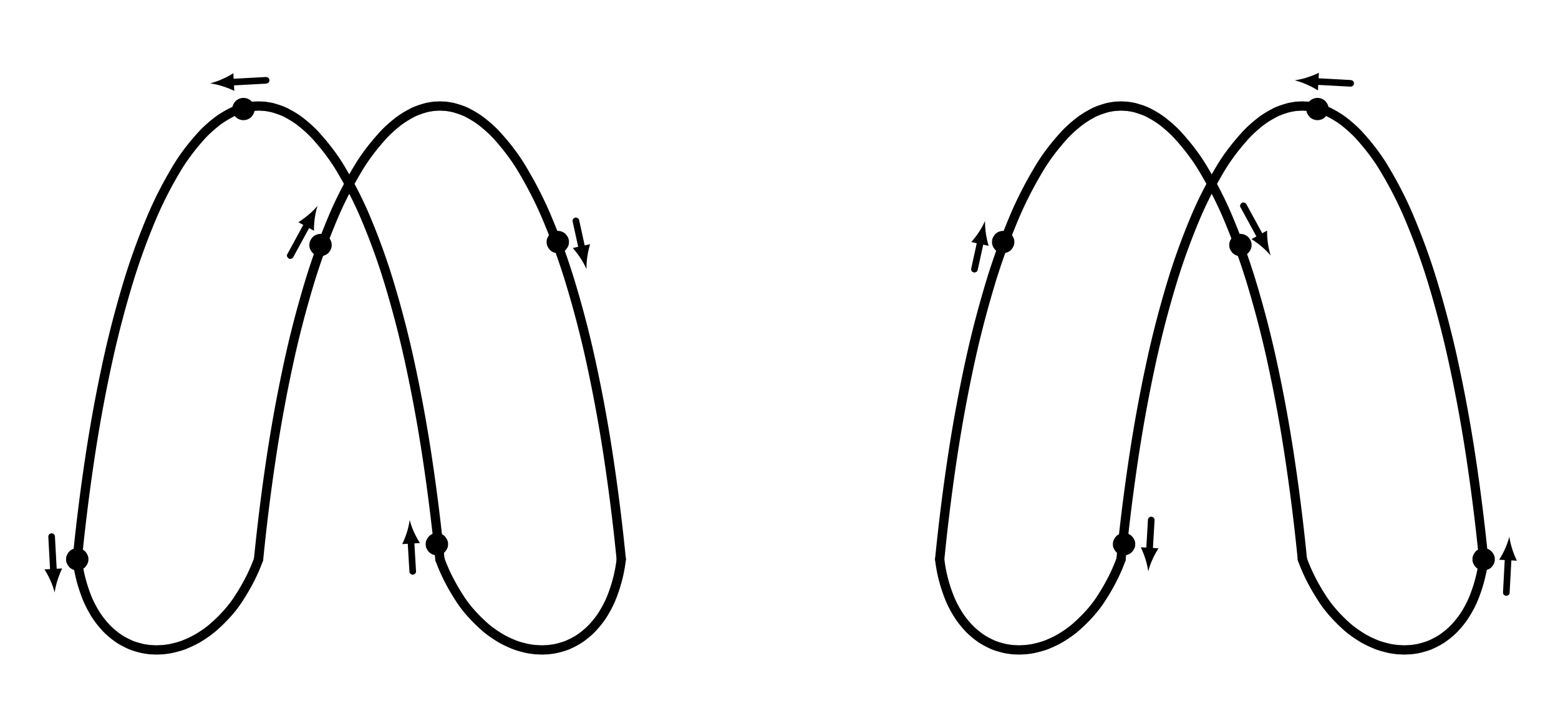
The cascade is a juggling pattern with an odd number of balls, each traversing a figure-eight pattern (see figure below); the two versions are time-reversals of each other, but the normal version is intrinsically more natural for, at the very least, 95% of the population (for, it is sometimes conjectured, subtle kinematic or anatomical reasons).
Elwyn is the only person that I’ve met who learned the reverse five-ball cascade first before learning the usual one. Some people learn the reverse three-ball cascade first, though nowadays this is rare because the usual one is taught in any class-like environment. Either five-ball pattern requires months (or more, or much more) of persistent practice. Elwyn clearly had some combination of talent, extreme diligence, and the sort of independent single-mindedness (i.e., stubbornness) required to ignore advice, which he surely received, to do things the usual way.
Meeting him, and then talking to him about any number of things during my visits to UC Berkeley, did not disabuse me of any of my priors.
When I moved to Berkeley for two years in 1999 to serve as Deputy Director at MSRI, Elwyn was helpful in quickly bringing me up to speed on the Berkeley campus and MSRI’s place in it. We talked frequently, and it was natural for David Eisenbud, MSRI’s Director, to draft the two of us into writing a puzzle column for the Emissary, MSRI’s newsletter.
This was a blast. I could count on having twice-yearly bursts of emails and phone conversations about problems and solutions. This was sometimes a demanding exercise, but we both enjoyed hearing what the other had to say. And he was extraordinarily fair-minded — for example, in conceding a point on those rare occasions when he was wrong.
These exchanges continued for 20 years, right up to a few days before his death when he signed off on the final draft of the Spring, 2019 column from a hospital bed.
My wife, Danalee, has a number of recollections of Elwyn (beyond watching us chatter and/or squabble about the puzzle column) from our years in Berkeley. One was seeing Elwyn’s joy backstage after an event organized by MSRI, in which Steve Martin and Bob Osserman had an amusing conversation on various topics, most vaguely related to mathematics. This was (by plan) interrupted by Robin Williams barging onstage out of the audience. The idea of “organizing” Robin Williams is a non sequitur, and the ensuing zaniness was greatly amusing to the audience. Elwyn was ecstatic afterwards both because of the quality of the banter, but also because it was all such a marvelous showcase for mathematics.2
Danalee’s other recollection was of the time when Elwyn gave me a chess puzzle, in her presence, that he had devised. He was astounded when she came back the next day with a solution. Danalee felt that the required moves were alien to chess players perhaps because they did not follow standard patterns, so that in fact it was an advantage to barely know the rules. In any case, Elwyn was amazed.
My fondest memories of Elwyn over the last 20 years relate to the puzzle column. He was absolutely indefatigable in working on puzzles and their statements, and we spent lots of time debating their suitability for the column. He was delighted when a problem was cited in an academic paper (or when it was mentioned, in one case, in The New York Times). It would be fun to go through such highlights over those 20 years, but this would take a lot of space, and it feels more appropriate to focus on one specific question that arose in our work.
Elwyn noticed that a voting puzzle, that appeared in one of the earliest “hat problems” in our columns, seemed to have a remarkably clean answer. The resulting conjecture says that something nice happens that does not happen in the more usual context of binary error-correcting or covering codes.
If you’ve read this far, then I feel no guilt in veering off into explicitly stating this conjecture, because I know that Elwyn would approve. Some notation is needed. Let \( Q_n \) be the graph of the \( n \)-dimensional hypercube, whose vertices are the \( 2^n \) \( n \)-bit binary strings, and two such vertices are connected by an edge exactly when they differ in precisely one position. A Hamming ball (of radius one) consists of a vertex (called the center) together with its \( n \) neighbors. The problem of finding a maximal disjoint collection of Hamming balls is equivalent to finding binary error-correcting codes, and the dual problem of finding a minimal set of Hamming balls that cover every vertex is an example of finding optimal covering codes. Unless \( n \) is of the form \( 2^k-1 \) or \( 2^k \), the problem of finding the number of elements of either kind of optimal code is intractable as soon as \( n \) is at all large.
Motivated by the aforementioned voting puzzle, which is equivalent to finding a covering by a generalization of Hamming balls, define an octopus in \( Q_n \) to be a vertex (called its center) together with \( n \) edge-disjoint paths starting at the center. (Note that a Hamming ball is an octopus whose paths all have length 1.) An octopus covering is a set of edge-disjoint octopi such that every vertex of \( Q_n \) is either a center of some octopus, or the endpoint of one of the paths that emanates from an octopus center.
Note that each octopus covers at most \( n+1 \) points, so this is saying that the smallest possible number of octopi is always sufficient. In other words, Elwyn was conjecturing that, in the case of octopus covers, the happiest possible situation always holds. I am sure that Elwyn would love it if someone would prove this\( \ldots \)
Joe Buhler received a PhD in 1977 from Harvard University in algebraic number theory, taught at Penn State and Reed College, became Deputy Director at MSRI in 1999, and was Director of the Center for Communications Research in La Jolla, CA, from 2004–2017.