by Morton Brown
The Kline sphere characterization problem
A principal goal of topology has always been that of finding reasonable sets of axioms for topological characterizations of standard topological spaces. Of course attention was first focused on the simpler spaces: the interval, the line, the circle. Once the basic notions of separation and compactness were worked out, these problems became quite tractable. The circle, for example could be characterized as a continuum (compact and connected metric space) which is non-degenerate (that is, not a point) and is separated by each pair of points. Two dimensional spaces such as the 2-sphere presented a much more challenging set of problems. This was a principal focus of topology in the first third of this century. Indeed, R. L. Moore’s book can be interpreted as a sweeping and historical definition of the plane, starting from first concepts.
By the mid-thirties, there were several satisfactory characterizations of the 2-sphere, but the most elegant one, suggested by J. R. Kline, remained unsolved: Suppose that a nondegenerate Peano continuum \( X \) is separated by each topological 1-sphere in \( X \), but is separated by no topological 0-sphere; is \( X \) a 2-sphere? It followed from work of Zippin, and van Kampen (see [1]) that the answer is affirmative if no arc separates \( X \). Many topologists attempted to remove this last condition. Bing succeeded.
This result, obtained shortly after his Ph.D., received much attention. Bing was marked as a young mathematician of great promise. That promise was well kept.
Bing’s work on the pseudo-arc
The postwar period in Poland (1920s) was one of fabulous development in topology. A principal interest was the study of plane continua, both “well behaved” (that is, locally connected) and pathological. Somewhat reflecting the audacity of the time were the following two questions:
- If a non-degenerate plane continuum is homeomorphic to each of its nondegenerate subcontinua, is it necessarily an arc?
- If a nondegenerate plane continuum is homogeneous, is it necessarily a simple closed curve?
The first question was raised by Masurkiewicz in volume 2 of Fundamenta Mathematica, the other was raised by Knaster and Kuratowski in volume 1.
There can be little doubt that these questions were regarded as tough nuts, and that they were vigorously attacked. The 288 pages of volume 2 of Fundamenta that separates these questions contains five papers by Kuratowski, Knaster, and Mazurkiewicz on related problems. Volume 3 includes a paper by Kuratowski on homogeneity. The same volume has, in successive papers by Knaster, two famous examples of exotic continua.
These Knaster continua have historical importance. A continuum is called “decomposable” if it is the union of two proper subcontinua. On first thought it would be reasonable to assume that every continuum is decomposable, but the existence of indecomposable continua was discovered by Brouwer in his disproof of the conjecture of Schönflies, that the common boundary of two plane regions is decomposable. Knaster’s first example, now called the bucket-handle or \( U \)-continuum, is an elegant and probably the simplest example of a plane indecomposable continuum, that is, a continuum in the Euclidean plane that is not the union of two proper subcontinua. The second example, constructed as the intersection of a decreasing sequence of bands, each very crooked inside its predecessor, has the further property that it is hereditarily indecomposable, that is, each of its subcontinua is indecomposable. It plays a special role in this talk, so I shall refer to it as the Knaster continuum.
Volume 3 of Fundamenta contains a long paper by Kuratowski on various properties associated with indecomposable continua. There is every reason to believe that Kuratowski, Knaster, Masurkiewicz et al. had strong suspicions that, if the questions (1) and/or (2) have negative answers, then the counterexamples would be as exotic as Knaster’s but, as we shall see, the truth is more astonishing than they could have suspected.
Problem (1) proved to be quite intractable, and perhaps began to be perceived as unnatural, in the sense that neither a positive nor negative answer seemed likely to influence future research. Some headway was made, notably by Whyburn, but despite an attempt by Wilder in 1937 to popularize the problem, it was to remain unsolved for another ten years.
Problem (2) attracted more attention. The hypothesis of homogeneity seemed to offer more to work with, and the fact that the problem could be recast in terms of a group action (the transitivity of the homeomorphism group) made the problem seem natural (in the sense that a positive or negative answer might direct future research). Although Mazurkiewicz proved in 1924 that the answer is affirmative if the continuum is locally connected, there was little further progress. In fact, the situation was obscured by an unfortunate succession of papers containing false results involving several authors.
In 1947, Moise in his Ph.D. dissertation (Trans. A.M.S. 63 (1948), pp. 581–594) described a general construction which produced a family of topologically equivalent plane continua having the property that they were hereditarily indecomposable and homeomorphic to each of their nondegenerate subcontinua, thus negatively settling problem (1). He noted that the Knaster continuum (which, by the way, had been in Knaster’s dissertation) was very similar, if not in fact topologically equivalent, to Moise’s continuum.
Moise’s methods were of course more powerful than Knaster’s. Instead of Knaster’s bands, Moise used a sequence of “chains” of open sets to define his “pseudo-arcs.” These chains were refined by chains whose patterns became successively more crooked with respect to the preceding chains. This guaranteed that the continuum would be hereditarily indecomposable. By a process of “consolidation” (the principle being that a sufficiently crooked chain could be consolidated into a chain of required pattern, as needed), Moise showed that all continua constructed in this way, that is, all pseudo-arcs, are homeomorphic. He then showed that each nondegenerate subcontinuum of a pseudo-arc is a pseudo-arc, and hence homeomorphic to it.
I must confess at this point that my understanding of Moise’s work is retrospective, and influenced by Bing’s subsequent papers. The full import of Moise’s construction was obscured by several factors. Moise’s chains did not cover the continuum, their closures did, but the links were pairwise disjoint. This complicated the constructions, and made their symmetry less transparent. Furthermore, the exposition, while lacking no precision, was not a model of clarity. The hypothesis of Theorem Nine, for example, takes some 270 words.
Bing must have coped with these difficulties as he tried to follow Moise’s proof. My guess is that he tried to recast Moise’s ideas into more comprehensible bits, and fit the ideas clearly into place. Bing [2] defined the pseudo-arc using chains of open covers and formalized the notion of pattern. By an intricate and subtle use of consolidations, he succeeded in proving that the pseudo-arc is actually homogeneous! (It should be mentioned here that, having seen Bing’s paper, Moise showed that homogeneity could also be deduced from his work.)
In a later paper, Bing [4] put the final piece of the puzzle in place. He showed that the pseudo-arc is the only hereditarily indecomposable chainable continuum. This meant that Knaster’s continuum is a pseudo-arc. In other words, Knaster’s continuum is a counterexample to both problems (1) and (2). (It is an interesting coincidence that, as partial requirements for their Ph.D., both Knaster and Moise submitted the same example.)
The pseudo-arc is one of the most fantastic and unique constructions in topology. Like the Cantor set, the pseudo-arc has a simple description, a fractal construction, is homogeneous, and is ubiquitous. Like an arc, it doesn’t separate the plane, is homeomorphic to each of its proper subcontinua, and has the fixed point property. Like a simple closed curve, it is homogeneous and has arbitrarily small open covers of circular chains. It is ubiquitous. (Bing showed [4] that, in the category sense, almost all continua are pseudo-arcs. Wayne Lewis recently proved that, in the category sense, almost every map between continua is an embedding of one pseudo-arc into another.) A principal theme of this conference is the interaction of continua theory and dynamical systems. The discrete dynamics of the pseudo-arc is likely to produce some remarkable phenomena.
Bing’s work on homogeneity
The exciting developments concerning the pseudo-arc naturally fueled the search for other homogeneous plane continua. Were they now all known, the circle and the pseudo-arc? Bing [4] suggested a circular version of the pseudo-arc, called the pseudo-circle, as a possible example. At first blush, this continuum would appear a more likely candidate than the pseudo-arc itself, but Fearnley (Bull. A.M.S. 75 (1969), pp. 554–558) and Rogers (Trans. A.M.S. 148 (1970), pp. 417–428) independently proved that it was not homogeneous. However, in 1954 Bing and Jones independently constructed another homogeneous continuum, the “circle of pseudo-arcs” [11]. In the 33 years succeeding the Bing–Jones example, much progress has been made in the search for homogeneous plane continua, notably by Jones and his school. Bing [11] returned to this problem in 1960 and proved that the circle is the only homogeneous plane continuum that contains an arc. The list of known examples still stands at three, and the list of possible types of examples has been shortened, but the problem remains unsolved.
Bing’s work on metrization
R. L. Moore’s students were introduced to topology via “Moore spaces” rather than Hausdorff spaces. In modern terminology, a Moore space is a regular Hausdorff space with a sequence \( G_1, G_2, \ldots \) of open covers such that for each point \( x \) and neighborhood \( N(x) \) there is an \( n \) such that every element of \( G_n \) that contains \( x \) lies in \( N(x) \). It was a question of long standing whether a normal Moore space is metrizable. Many of Moore’s students and grand-students (and Moore himself) worked on this problem. Bing, of course, also worked on this problem, but did not solve it. This is forgivable (as it is indeed for all of those who attempted it), as the problem turned out to be undecidable. However, in working on it, Bing [3] developed a very interesting property which he called “collectionwise normal.” A Hausdorff space is collectionwise normal if each discrete collection of pairwise disjoint closed sets can be covered by pairwise disjoint open sets. He then proved that a collectionwise normal Moore space is metrizable, then gave a beautiful example of a normal Hausdorff space that is not collectionwise normal.
In the same paper (and in the same spirit) was the following theorem, now known as the Bing Metrization Theorem: A necessary and sufficient condition that a regular Hausdorff space be metrizable is that it have a sigma-discrete basis, that is, a basis \( G = \bigcup G_n \) such that each \( G_n \) is discrete. Independently, Nagata and Smirnov derived similar results with “locally finite” replacing “discrete.”
Bing’s work on convex metrics
A convex metric space is a metric space in which, for each two points \( a \) and \( b \), there is a third point \( c \) such that \( d(a,b) = d(a,c) + d(c,b) \). In 1928, Menger had proved that a compact convex metric space is a Peano continuum, and asked whether the converse were true: Does each Peano continuum have a convex metric? This problem received much attention. There was a discussion of it in Blumenthal’s book, Distance geometries (1938), and partial results were established by Kuratowski, Whyburn, and Harrold. In 1938 Beer published an affirmative solution for the one-dimensional case.
In 1948, Bing was at Madison, and Moise at Ann Arbor. Both were working on the Menger problem. Bing published an affirmative solution in 1949 for the finite-dimensional case. Shortly afterward, Moise announced a proof for the general case, and a few weeks later Bing announced his proof. Their papers appeared back to back in the A.M.S. Bulletin. Unfortunately, Moise’s paper had a serious error. Interestingly, both papers employed the notion of what Bing called “partitioning.” This notion of pairwise-disjoint open sets whose closures cover the space is reminiscent of Moise’s approach to the pseudo-arc.
We now get to the area that was to dominate Bing’s interest for the rest of his career.
Bing’s papers on 3-manifolds (triangulation and taming)
In a talk he gave in 1955, Bing expressed his views on the direction he felt that geometric topology should take:
There has been much study devoted to the plane, and simple problems that have not already been attacked are difficult to find in this area… On the other hand, \( \mathbb E^3 \) is essentially a virgin forest. For many years the problems were so forbidding that few attacks were successful. Now mathematicians are beginning to venture into the woods.
In 1949 Bing had visited the University of Virginia and, according to Bing, he became interested in 3-space after conversations with Ed Floyd. In the meantime, Moise had turned his interest to \( \mathbb E^3 \) and had broken hard ground with his monumental series of papers, “Affine structures on 3-manifolds” (Annals of Math., 1951–1954). Moise had triangulated 3-manifolds (without boundary) and proved the Hauptvermutung for 3-manifolds. Bing had published his paper on the sum of two horned spheres in 1952 (I will return to this paper in a later section) and in 1954 Bing had published his first major paper on triangulation, “Locally tame sets are tame” [5]. This paper appeared back to back in the Annals of Math. with Moise’s “Affine structures…” The content of both these papers is similar, and both papers leaned heavily on Moise’s earlier work.
For simplicity of exposition I shall describe the results in \( \mathbb E^3 \), although the proofs work in an arbitrary triangulated manifold. A subset \( K \) of \( \mathbb E^3 \) is called tame if there is a homeomorphism of \( \mathbb E^3 \) carrying \( K \) onto a polyhedron. It is called locally tame if, for each point \( p \) of \( K \), there is a neighborhood \( N(p) \) and a homeomorphism of the closure of \( N \) into \( \mathbb E^3 \) that carries both the closure of \( N \) and its intersection with \( K \) onto polyhedra. The main theorem is the title of Bing’s paper. Another important result in their papers is that each 3-manifold with boundary can be triangulated, extending Moise’s work to manifolds with boundary. (This result is needed, for example, to prove the annulus theorem in three dimensions, although the problem was not explicitly formulated at the time.)
In 1955, at the time of the quotation at the beginning of this section, Bing [7] had just proved his Approximation Theorem for Surfaces: If \( M \) is a 2-manifold with boundary in a triangulated 3-manifold \( S \), and \( f \) is a non-negative continuous function defined on \( M \), then there is a manifold \( M^{\prime} \) and a homeomorphism \( h \) of \( M \) onto \( M^{\prime} \) such that \( M^{\prime} \) is locally polyhedral at \( h(x) \) if \( f(x) > 0 \) and \( d(x,h(x))\leq f(x) \). This theorem will play a fundamental role in Bing’s work. At a crucial place it uses Moore’s plane decomposition theorem.
In 1959, Bing published his “Alternative proof that three-manifolds can be triangulated” [9]. A key ingredient of this paper is a strengthening of the approximation theorem for manifolds, to an approximation theorem for 2-complexes; that is, the manifold of the previous result is replaced by an arbitrary topologically embedded 2-complex. The paper is a completely self-contained proof of both the triangulation theorem and Hauptvermutung for 3-manifolds with or without boundary. It also establishes that each homeomorphism of a 3-manifold can be approximated by piecewise-linear ones (Moise had done this in the unbounded case).
Roughly speaking, Bing’s early papers in this area rely on Moise’s main results from “Affine structures, 1–5.” By 1954, they are working independently and getting similar results. After Bing’s “Alternate proof that three manifolds can be triangulated,” their work takes different directions.
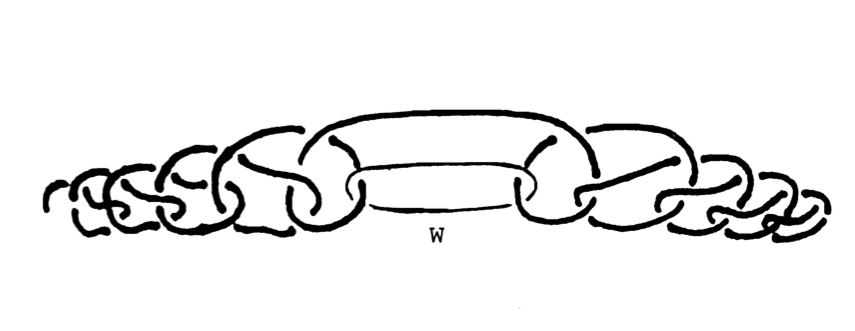
In 1958, Bing [8] published his “Necessary and sufficient conditions that a 3-manifold be \( \mathbb S^3 \).” In order to put this paper into perspective, it will be necessary and, I hope, sufficient to recall The Fox–Artin arc (Annals of Math. (1948), pp. 979-990) which has a simply connected complement in \( \mathbb S^3 \) even though its complement is not \( \mathbb E^3 \) (see Figure 1).
Fox and Artin showed that the simple closed curve \( W \) in the complement of the arc is null-homotopic, but there is no homeomorphism of the complement of the arc that transforms \( W \) into the interior of a ball. “It seems to us that the existence or non-existence of a closed simply connected three-dimensional manifold with this property would be a decisive point in solving the Poincaré Conjecture.” Bing’s theorem is that a closed 3-manifold is \( \mathbb S^3 \) if each simple closed curve lies in a topological 3-ball. It is a sharp theorem, of the form: \( (\pi_1(M) = 0) + \varepsilon \) implies \( M = S^3 \). Bing suggested, and McMillan later proved, that an even sharper hypothesis suffices: every simple closed curve is null-homotopic within some solid torus.
In 1958, Bing [17] proved the powerful Side Approximation Theorem: If a 2-sphere is in \( \mathbb E^3 \) and \( \varepsilon > 0 \), then there is an \( \varepsilon \)-homeomorphism of the sphere into a polyhedral one which is strictly on a given side of the sphere, except possibly for a finite number of \( \varepsilon \)-disks.
Bing used this result to prove that
- each disk in \( \mathbb E^3 \) contains a tame arc [16];
- each disk in a \( \mathbb E^3 \) is pierced by a tame arc [15];
- a surface (or a Cantor set) is tame if its complement is 1-ulc [14], [13].
The 1-ulc paper [14] can be called the real beginning of taming theory. It is at the root of much of the development of higher-dimensional topology.
Another fundamental result of Bing’s in taming theory is the theorem that a 2-sphere in \( \mathbb E^3 \) is tame if it can be approximated by spheres (not necessarily tame) from either side. Let me leave this subject by observing that Bing and his students found a number of remarkable applications of these ideas.
Bing’s work on decomposition spaces
In the 1920s R. L. Moore proved the following: If \( G \) is an upper semicontinuous decomposition of the plane into continua, not one of which separates \( \mathbb E^2 \), then the decomposition space is \( \mathbb E^2 \). (A partition of a space into continua is upper semicontinuous if each continuum in the collection is “at least as large” as nearby continua; that is, if \( N(C) \) is a neighborhood of a continuum in the partition, then there is a smaller neighborhood \( V(C) \) such that each continuum in the partition intersecting \( V(C) \) lies in \( N(C) \). The decomposition space is the quotient space obtained by identifying each of the continua to a point.) The proof was as follows: Using a topological characterization of the plane, Moore proved that the decomposition space satisfies the same axioms. This of course is an oversimplification! The proof has been described as a tour de force of 2-dimensional topology.
The corresponding problems for \( \mathbb E^3 \) were at the heart of Bing’s mathematical interest throughout his career: What is a simple useful topological characterization of \( \mathbb E^3 \), and which monotone decompositions (that is, compact connected decomposition elements) of \( \mathbb E^3 \) produce a decomposition space homeomorphic to \( \mathbb E^3 \)?
Whyburn had observed that even with only one nondegenerate decomposition element, a simple arc, the decomposition space might not be \( \mathbb E^3 \). (For example, if \( a \) is the Fox–Artin arc previously mentioned, then \( \mathbb E^3/a \) is not \( \mathbb E^3 \), as \( \mathbb E^3 - a \) is not simply connected.) Whyburn suggested that, perhaps, one should therefore study “pointlike” decompositions of \( \mathbb E^3 \), that is, those in which the complement of each element is homeomorphic to the complement of a point. In fact, using this terminology, Moore’s theorem becomes: Each pointlike (upper semicontinuous) decomposition of \( \mathbb E^2 \) has \( \mathbb E^2 \) as its decomposition space. As for topological characterizations of \( \mathbb E^3 \), Wilder had postulated that the space should have the local homology groups of 3-space (that is, a generalized manifold), but no-one seemed to have even a good suggestion for a simple set of axioms (nor is there one at this time!).
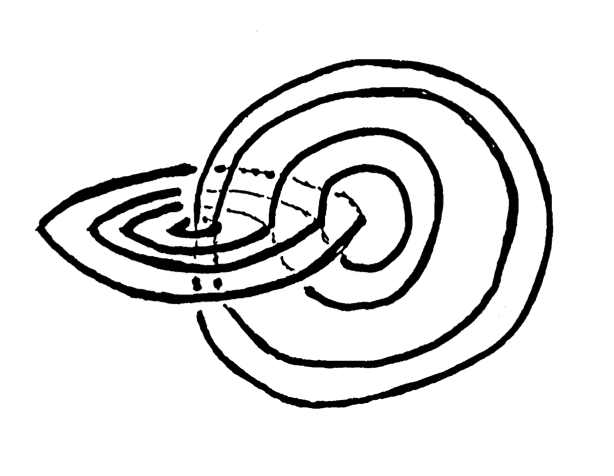
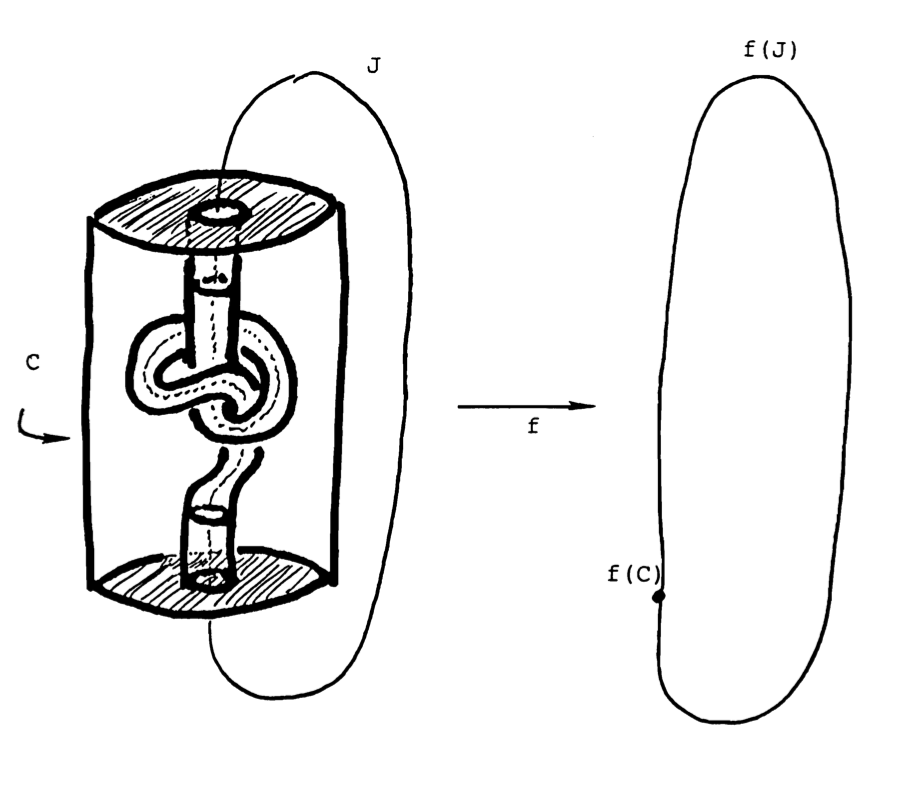
Figures 2 and 3 illustrate two subtle aspects of decomposition theory.
Figure 2 illustrates a striking example (due to Bing \citeyear{36}) of a monotone decomposition of \( \mathbb E^3 \) into points, circles, and figure-eights. The decomposition space is \( \mathbb E^3 \) even though the two circles link. Bing and Moise gave entirely different proofs of this (Institute in Set Theoretic Topology, 1955) and each proof is a lesson in the subtlety of decomposition theory.
In the second example, due to the author, there is only one decomposition element, and it is pointlike, so the decomposition space is \( \mathbb E^3 \). But the quotient map carries the knotted arc \( J \) homeomorphically onto an unknotted arc. Bing was to discover an even more subtle fact: it is possible to “link” bunches of arcs together even though each pair in the bunch is polyhedral. But I am getting ahead of the narrative.
Bing’s very first paper on \( \mathbb E^3 \) (1951) was an attempt to provide at least some set of axioms. Unfortunately, the axioms were not particularly useful or illuminating. His second paper, however, was a blockbuster. Bing showed that \( \mathbb S^3 \) is the union of two solid horned spheres sewn together along their boundary. First of all, the construction provides an involution of \( \mathbb S^3 \) whose fixed-point set is a horned sphere, that is, an involution that could not be conjugate to a linear involution. An important consequence of this construction was that the theory of transformation groups moved in the direction of differential topology in order to avoid pathology.
But it was Bing’s method of proof that was both startling and seminal. He used “decomposition theory.” Bing constructed a certain pointlike decomposition of \( \mathbb E^3 \) and showed that (1) the decomposition space could be viewed as the union of two horned spheres, and (2) the decomposition space is homeomorphic to \( \mathbb E^3 \). The method that Bing used to prove (2) involved a procedure whereby the decomposition elements were gradually “shrunk” to smaller sets without allowing the other decomposition elements to grow too large. This technique grew into what McAuley later named “Bing’s shrinking criterion.”
Let’s stop for a moment and see what the situation would have been if the decomposition space were not \( \mathbb E^3 \). In that case Bing would have constructed a decomposition of \( \mathbb E^3 \) into points and tame arcs whose decomposition space is not \( \mathbb E^3 \), showing that Whyburn’s suggested version for a Moore Theorem in \( \mathbb E^3 \) would not work. Thus, Bing had a major result whichever way it came out.
When it turned out that the decomposition space was \( \mathbb E^3 \), Bing immediately started trying to frustrate this outcome, that is, he tried to frustrate the shrinking trick. The result of his efforts was perhaps Bing’s greatest construction, the dogbone space [6]. The decomposition elements are still points and tame arcs, but they cannot be shrunk uniformly small. Bing showed that if the decomposition space were \( \mathbb E^3 \), then it would be possible to shrink the elements. (This was a negative application of the shrinking criterion.) In his argument, Bing used a delicate property of \( \mathbb E^3 \): a certain pair of intersecting disks could be “adjusted” so that they became disjoint. This would be possible if the decomposition space were \( \mathbb E^3 \). But Bing showed that that would lead to a contradiction, so that the decomposition space does not satisfy a “disjoint disc” property and, hence, is not \( \mathbb E^3 \). The decomposition space is, in fact, not a manifold at any of the nondegenerate “points.”
But Bing’s interest in the dogbone space did not end with this achievement. He was determined to understand the extent to which the decomposition elements were linked, and what delicate properties of 3-space were involved. What he proved (in a paper [10] that is most difficult to read, even though it is excellently written) was that the Cartesian product of the dogbone space and a line is \( \mathbb E^4 \). Whitehead had constructed a famous example of a contractible open subset of \( \mathbb E^3 \) which is not homeomorphic to \( \mathbb E^3 \), and Arnold Shapiro had recently shown that the product of this space with a line is \( \mathbb E^4 \). This was startling: \( \mathbb E^4 \) had factorings other than \( \mathbb E^1 \times \mathbb E^3 \) and \( \mathbb E^2 \times \mathbb E^2 \). What Bing showed was that the dogbone space was a factor of \( \mathbb E^4 \). In other words, \( \mathbb E^4 \) has non-manifold factors. The proof involved a very elaborate application of the shrinking criterion.
These three papers were of fundamental importance in the development of three-dimensional topology, but they also contained some of the seminal ideas that were at the heart of the great accomplishments of higher-dimensional geometric topology of the late 1970s: decomposition spaces, shrinking criteria, stabilization of decomposition spaces (that is, non-manifold decomposition spaces whose product with \( \mathbb E^n \) were Euclidean), and the disjoint-disk property. In Michael Freedman’s Veblen Prize speech, he pays tribute to the critical role that Bing’s decomposition theory played in Freedman’s solution of the four-dimensional Poincaré Conjecture. “Bing shrinking” played a key role in Torunczyk’s work in \( Q \)-manifolds. Interestingly, one of his theorems (An ANR in Hilbert space is a manifold if and only if it has the “discrete-cells property”) not only uses Bing shrinking, but is reminiscent of Bing’s “collectionwise normal” condition. Cannon and Edwards have given us a marvelous view of higher-dimensional manifolds. As they have acknowledged, they too were standing on Bing’s shoulders.
Other papers
Although Bing’s primary concern was to remain with the topology of \( \mathbb E^3 \), he kept a lively interest in all areas of geometric topology and continua theory.
One of the results of the renaissance of infinite-dimensional topology in the 1960s was the solution of a problem that went back at least 40 years: Is real Hilbert space homeomorphic to the countable infinite product of real lines? The problem was explicitly raised by both Frechet and Banach in their famous books. Although the question must have arisen countlessly in classrooms, there seems to have been little progress toward its solution before 1960. Finally, in 1966, R. D. Anderson gave an affirmative solution. It was a culmination of the work of several authors, notably Anderson, Bessaga, Kadec, and Pelcynsky.
Bing, of course, was very interested in understanding a proof of this theorem, and in 1968 Anderson and Bing published a self-contained and completely elementary proof of this result. The paper appeared in its entirety in the Bulletin of the A.M.S., upon invitation of the editors [18].
The monotone-mapping problem was another highly respected problem. In 1959, Whyburn had proved that if a map takes \( \mathbb E^2 \) to \( \mathbb E^2 \) and the inverse of each point is compact and connected, then the inverse of each compact set is necessarily compact. He asked whether the same result is true for \( \mathbb E^n \). In 1969, Glaser gave a negative answer for \( n > 3 \). Later in the same year, Bing [20] gave a difficult and ingenious counterexample for the case \( n = 3 \).
Of course, fixed-point problems are never far from the heart of geometric topologists, and Bing made a significant contribution in this area, without ever publishing a research paper to my knowledge. He did publish an expository paper in the American Math Monthly in 1969, called “The elusive fixed point property” [19]. Reviewing 23 theorems and raising twelve questions, it is a model of exposition. Each of the questions subsequently has received attention in the literature, and one method casually employed by Bing, the “dog chases rabbit” technique, has been exploited frequently and fruitfully, by Hagopian, for example.
Bing’s expository style is an important part of his mathematical “work.” It is always informal, while intensely rigorous. The proofs do not cover the tracks of discovery. Papers will often explain (with examples) why a certain alternative path would run into trouble. The title is often the main result. Bing’s lecturing style, his expository style, and his conversational style were disarmingly geared toward clarity of thought and simplification of exposition. His Colloquium book [21] reflects this quality. Reading it, one has the feeling of a conversation with the author. Bing’s persona leaps out of the pages.
In conclusion I would like to share with you some quotations that I have gleaned in preparing this talk.
- Bing, “The pseudo-arc,” 1955: “The set of all bounded continua (as arcs, discs, spheres points, etc.) that differ from the pseudo-arc is only of the first category. This being the case, if a person dealing with a continuum whose shape is unknown (as a physicist dealing with one of the obsolete treatments of the atom), it might be more reasonable to suspect it to be in the shape of a pseudo-arc than to suspect it to be spherical.”
- Bing, “Decompositions of \( \mathbb E^3 \),” 1965: “I had hoped that others writing about the dogbone space would give a more elegant proof that it was topologically different from \( \mathbb E^3 \). Several have not availed themselves of this opportunity.”
- Bing, “The monotone mapping problem,” 1965: “Perhaps \( \mathbb E^3 \) sheds more light on \( \mathbb E^n \) than \( \mathbb E^n \) sheds on \( \mathbb E^3 \).”
- Michael Freedman, Veblen prize acceptance speech, 1986: “But I owe a special debt to Bob Edwards, who taught me the branch of geometry, ‘Bing topology,’ which plays a central role in the work which the A.M.S. has recognized with this reward.”
- J. W. Cannon, I.C.M. Helsinki, 1978: “We explained our work to Bing. He was not excited. He found the proof obscure. In frustration we sought the simplest possible conceptual framework encompassing the mildly wild 1-ulc taming properties, and the disjoint disk decomposition properties became clear in our minds and the characterization conjecture immediately took its present form.”
-
Bing, “What topology is here to stay”, 1955:
“As topology grows we should grow with it. We should continue to learn new methods of attack and new results. This does not mean
that we should flip-flop from one field of mathematics to another, trying to find something easy to do. The river that cuts a deep furrow, that leaves a lasting
impression, is one that follows a steady course and does not meander all over the map.
Those of us who are to be successful in research must remain students. Our universities are turning out too high a percentage of “finished products”… people whose training is finished when they graduate… Perhaps it is more important to provide students with the ability and stimulus to be active researchers than that it give them a broad background.”
R H Bing’s contribution to research was eminent, and inherent in that eminence is that teaching was never far from his mind, and he was a great teacher. Those of us who are his students, his colleagues, his mathematical friends, all share the benefits of that greatness.