Celebratio Mathematica

I first meet Joan Birman in the Fall of 1985. I had been at the Uni­versity at Buf­falo as an as­sist­ant pro­fess­or for one year. Its math­em­at­ics de­part­ment had a laud­able his­tory of re­search in clas­sic­al point set to­po­logy and found­a­tions. But, my hire showed the de­part­ment’s in­terest in ex­pand­ing in­to geo­met­ric to­po­logy. With this in mind and know­ing of Joan’s work in low di­men­sion­al to­po­logy and braids, I in­vited her up to Buf­falo to give the de­part­ment’s col­loqui­um. Al­though it was a short vis­it we man­aged to talk a good deal of math­em­at­ics and Joan gave me a peek in­to the large world of braids. She told me of the Jones’ con­jec­ture — I would end up pur­su­ing it for the next $20+$ years. Simply stated, the con­jec­ture claims that the al­geb­ra­ic length of a min­im­al in­dex closed braid rep­res­ent­at­ive of an ori­ented knot is an in­vari­ant of the knot. Drop­ping her off at the air­port, Joan said “maybe we can do some work to­geth­er”. Fam­ous last words. We went on to co-au­thor 13 pa­pers and two more manuscripts where we were joined by ad­di­tion­al col­lab­or­at­ors.

After our ini­tial meet­ing, we were in steady com­mu­nic­a­tion for a num­ber of months. This was be­fore the ad­vent of email, so we talked on the phone a good deal and used snail-mail. Ad­di­tion­ally, we star­ted rack­ing up the fre­quent fli­er miles, me go­ing down to New Rochelle to stay at the Birman house­hold, and Joan com­ing up to Buf­falo and stay­ing at my home. Our vis­its were filled with math, cook­ing and con­ver­sa­tion over fam­ily meals. I be­came good friends with Joe, Joan’s hus­band, and Joan saw my wife, Melissa, and me raise our two boys, Timothy and Ry­an.

Early in our dis­cus­sions I asked Joan if she had a big “dream” con­jec­ture. Her reply was that she hoped to be able to use closed braids in solv­ing the knot clas­si­fic­a­tion prob­lem — a simple ver­sion of this is, give an ef­fect­ive al­gorithm for de­term­in­ing when two knots in $S^3$ are iso­top­ic. Garside’s solu­tion to the con­jugacy prob­lem sup­plied the means for de­cid­ing when two $n$-braids were in the same con­jugacy class; that is, when one giv­en $n$-braid is iso­top­ic in the com­ple­ment of its braid ax­is to a an­oth­er giv­en $n$-braid. Markov’s the­or­em told us that two closed braid rep­res­ent­at­ives of the same knot type are iso­top­ic through a se­quence of sta­bil­iz­a­tions, destabil­iz­a­tions and braid iso­top­ies. Markov’s the­or­em had been es­sen­tial to Vaughn Jones’ proof that his knot poly­no­mi­al was a knot in­vari­ant. But, sta­bil­iz­a­tion-destabil­iz­a­tion se­quences were a “black box”. What did sta­bil­iz­a­tion buy you? In one of Joan’s earli­est let­ters to me she wrote: “In my book, page-100, ex­ample 2-27, you’ll find a se­quence of moves which real­ize an ex­change by go­ing up [in in­dex] once and then down [in in­dex] again.” [1] This one ex­ample, which I think was ori­gin­ally due to Jim Van Buskirk, was the basis for Joan’s hunch that there ex­is­ted a closed braid cal­cu­lus — a set of “canned iso­top­ies” that al­lowed one to move between closed braid con­jugacy class rep­res­ent­at­ives of the same knot type without hav­ing to sta­bil­ize. Joan’s page-100 ex­change move was just one such canned iso­topy. (See the next fig­ure. See [4] for a full dis­cus­sion of the cal­cu­lus.) Joan’s fo­cus on this one ex­ample il­lus­trates a qual­ity that I have al­ways re­cog­nized and ap­pre­ci­ated. She has a eye for where the math­em­at­ics is and where it should go.

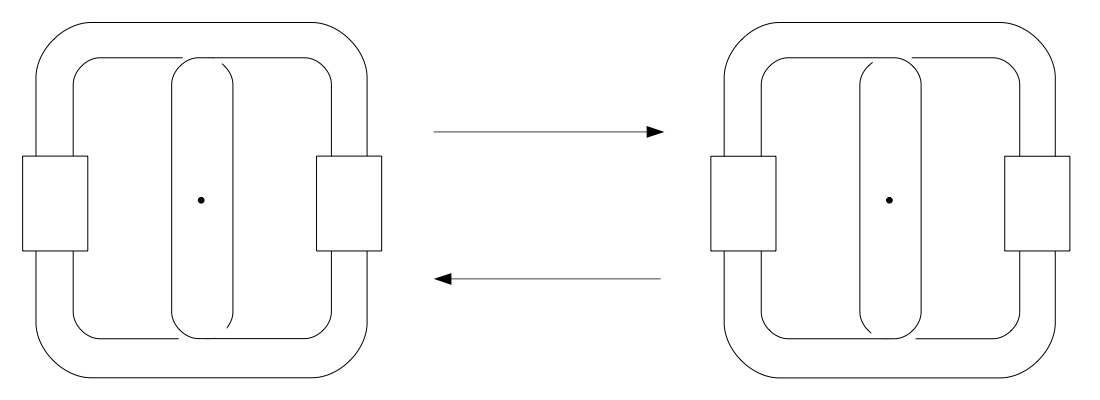
This idea of canned iso­top­ies seemed reas­on­able to me. My doc­tor­al thes­is had been on in­com­press­ible sur­faces in the com­ple­ment of al­tern­at­ing knots and I had Tait’s flyping con­jec­ture on the brain for some time. Work­ing out some low in­dex ex­amples we quickly real­ized that the cal­cu­lus for 3-braids had to be just braid pre­serving flypes. But, the prob­lem with all math­em­at­ics is how to turn a had in­to a proof. It took us some time to de­vel­op trac­tion. By the sum­mer of 1986, we thought we had some res­ults that we were go­ing to present at a UC Santa Cruz braid con­fer­ence, but we found a fatal flaw in our ar­gu­ment at the last minute and had to can­cel.

Fi­nally, in 1987 we star­ted to make some sub­stan­tial head­way. Us­ing ba­sic gen­er­al po­s­i­tion ar­gu­ments we con­sidered a span­ning sur­face of a closed braid and its in­ter­sec­tion with disc fibers of the braid fo­li­ation. Po­s­i­tion­ing the span­ning sur­face so that it is trans­verse to the braid ax­is and all but fi­nitely many disc fibers, one ob­tains a sin­gu­lar fo­li­ation on the span­ning sur­face that looks like the uni­on of four-sided tiles, each tile con­tain­ing a saddle-point where the sur­face and a disc fiber in­ter­sect non­trans­versely. The ver­tices (or corners) of these tiles were where the sur­face was punc­tured by the braid ax­is. There were nat­ur­al par­ity as­sign­ments to each tile and each ver­tex. With all of this com­bin­at­or­i­al in­form­a­tion the ques­tion was how to see when a braid ad­mit­ted a pos­sible canned iso­topy. We real­ized that the sin­gu­lar fo­li­ation had nat­ur­al loc­al ma­nip­u­la­tions that cor­res­pon­ded to braid iso­top­ies, sta­bil­iz­a­tions, destabil­iz­a­tions, and ex­change moves. We also real­ized that we had stumbled onto tech­no­logy that was es­sen­tially what Daniel Ben­nequin had de­veloped in his sem­in­al work on braids and con­tact geo­metry [e1], the one dif­fer­ence be­ing his sin­gu­lar fo­li­ation was in­duced by the stand­ard con­tact plane field in ${\mathbb{R}}^3$.

One key ob­ser­va­tion that Joan made was the tiling nature of the sin­gu­lar fo­li­ation yiel­ded an Euler char­ac­ter­ist­ic equa­tion which de­term­ined when an ex­change move or destabil­iz­a­tion must oc­cur. With the sin­gu­lar fo­li­ation and this Euler char­ac­ter­ist­ic equa­tion in hand we cranked out a “Study­ing links via closed braids” series of pa­pers [5], [3], [4], [7]. Spe­cific­ally, we es­tab­lished that if at a fix braid in­dex a link type has in­fin­itely many dis­tinct closed braid rep­res­ent­at­ive iso­topy classes then all but fi­nitely many of them were re­lated by ex­change moves. For closed braid rep­res­ent­at­ive of the $k$-com­pon­ent un­link we es­tab­lished that through a se­quence of braid iso­top­ies, destabil­iz­a­tions and ex­change moves, one could ob­tain the $k$-braid un­link. In [2] we re­placed the span­ning sur­face with an $S^2$ il­lus­trat­ing that the link was a split or com­pos­ite link. Spe­cial­iz­ing the sin­gu­lar fo­li­ation and Euler equa­tion to this sur­face we again es­tab­lished that all that was needed for mov­ing from an ar­bit­rary closed braid rep­res­ent­at­ive to one where the links de­com­pos­ing com­pon­ent were read­ily vis­ible were braid iso­top­ies and ex­change moves. This pat­tern of ex­change moves be­ing the primary sim­pli­fy­ing canned iso­topy held where we re­place $S^2$ with an es­sen­tial tor­us in the link com­ple­ment [9].

Since then sev­er­al schol­ars have modeled their in­vest­ig­a­tions on this strategy of hav­ing a sur­face tiling struc­ture powered by a Birman-M Euler char­ac­ter­ist­ic equa­tion. Both Peter Crom­well [e2] and Ivan Dyn­nikov [e8] used this strategy in their works on arc present­a­tions of knots. Tet­suya Ito em­ployed the tiling/Euler-equa­tion combo his very beau­ti­ful work which made con­nec­tions between the braid group or­der­ab­il­ity and es­sen­tial sur­faces in the knot com­ple­ment [e11], [e10], [e14]. And, I will men­tion oth­ers shortly.

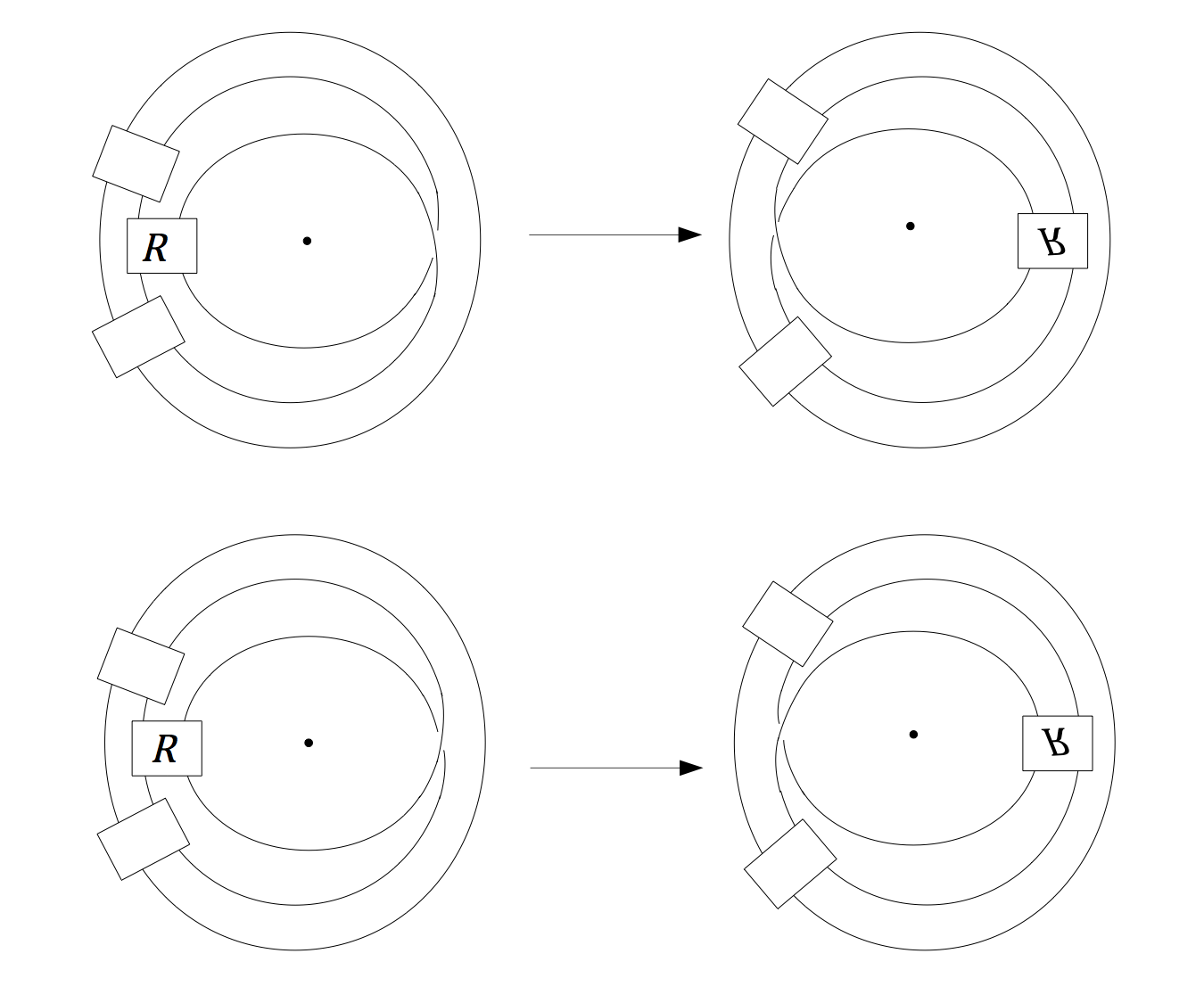
In our pa­per on 3-braids [8] we fi­nally came back to es­tab­lish­ing the closed braid cal­cu­lus for ori­ented links rep­res­en­ted by closed 3-braids. We were in­ter­ested in prov­ing what we real­ized from the start of our work, that cal­cu­lus for 3-braids had to be just braid pre­serving flypes. In fact, there are two types of braid pre­serving flypes —  pos­it­ive flypes and neg­at­ive flypes. This fact would be­come im­port­ant later when we star­ted to think about ap­plic­a­tions of our work to knot the­ory in the con­tact geo­metry set­ting. What al­lowed us to clas­si­fy closed 3-braids was an ob­ser­va­tion that was made ori­gin­ally by D. Ben­nequin — a min­im­al genus span­ning sur­face of 3-braid in­ter­sects any 3-braid ax­is ex­actly three times [e8], [3]. Our ar­gu­ment then fo­cused on an ana­lys­is of how two axes rep­res­ent­ing dis­tinct 3-braid con­jugacy classes could pos­sibly in­ter­sect the same min­im­al genus span­ning sur­face. The up­shot is that every closed 3-braid link has either one unique con­jugacy class, or two. And, if two then the two classes are re­lated by a braid pre­serving flype. (See the fig­ure above.) Later Ki-Hy­oung Ko and Sang-Jin Lee de­term­ined which 3-braids ad­mit­ted both pos­it­ive and neg­at­ive flypes [e4]. This be­came im­port­ant for our con­tact geo­metry ap­plic­a­tions, which I will come to mo­ment­ar­ily.

The clas­si­fic­a­tion of closed 3-braids par­tially opened the sta­bil­iz­a­tion black box. The 3-braid pre­serving flype cor­res­pon­ded to a fixed sta­bil­iz­a­tion se­quence — sta­bil­ize pos­it­ively (resp. neg­at­ively), fol­lowed by a par­tic­u­lar 4-braid iso­topy, fol­lowed by a pos­it­ive (resp. neg­at­ive) destabil­iz­a­tion for a pos­it­ive (resp. neg­at­ive) flype. (See [10] for se­quence.) So the closed 3-braid cal­cu­lus was fi­nite — one canned iso­topy, or one tem­plate. By 2002 we thought we were ready to write down the de­tails of the Markov The­or­em without Sta­bil­iz­a­tion (MT­WS), which states the fol­low­ing. Let $(m,n)$ be any pair of pos­it­ive in­tegers with $0<n<m$. Let ${\beta }_1$ and ${\beta }_2$ be closed braid rep­res­ent­at­ive of the same link type with the braid in­dex of ${\beta }_1$ be­ing $m$ and the braid in­dex of ${\beta }_2$ be­ing $n$ which is min­im­al for the link type. Then there ex­ists a fi­nite col­lec­tion of iso­topy tem­plates de­pend­ing only on $(m,n)$ which can be used in an iso­topy se­quence of closed braid that move ${\beta }_1$ to ${\beta }_2$. And, here is the kick­er, the braid in­dex of this se­quence is nonin­creas­ing [6]. The proof of the MT­WS was a de­tailed ana­lys­is of a very simple proof of the Markov The­or­em that we put for­ward in a short pa­per [11]. The sa­li­ent new tech­no­logy that we in­tro­duced in this pa­per was the clasp an­nu­lus — an­nuli that cor­res­pond to an iso­topy between bound­ar­ies but which also has clasp self-in­ter­sec­tions.

The most im­me­di­ate ap­plic­a­tion of the MT­WS was to con­tact geo­metry and knot the­ory. A con­tact struc­ture on a smooth 3-man­i­fold is a smooth 2-plane field in the tan­gent bundle that is com­pletely non­in­teg­rabil­ity. The stand­ard con­tact struc­ture for ${\mathbb{R}}^3$ cor­res­ponds to the ker­nel of the 1-form, $\alpha =dz+r^{2}d\theta$, in cyl­indric­al co­ordin­ates and the stand­ard con­tact struc­ture for $S^3$ can be seen as the plane field that is nor­mal to the Hopf fibra­tion of $S^3$ by $S^1$’s. We in­cor­por­ate con­tact struc­tures in­to knot the­ory by con­sid­er­ing knots that are either totally trans­verse to the con­tact plane field —  trans­verse links — or totally tan­gent to the plane field —  Le­gendri­an links — and iso­top­ies that pre­serve these qual­it­ies. Daniel Ben­nequin in his sem­in­al work [e1] showed that every trans­verse link was trans­versely iso­top­ic to a braid rep­res­ent­at­ive. An im­me­di­ate in­vari­ant of a trans­vers­al knot class is the self link­ing num­ber. It was im­me­di­ately clear to Joan and me that the iso­topy tem­plate com­ing from the MT­WS could either cor­res­pond to a trans­vers­al iso­topy or not. A ne­ces­sary con­di­tion of a tem­plate to be trans­verse was that it must pre­serve the self link­ing num­ber. For ex­ample, Yakov Eli­ash­berg in 1998 had es­tab­lished that the trans­vers­al classes of the un­knot were clas­si­fied by the self link­ing num­ber. He had spec­u­lated in con­ver­sa­tion to Joan that knot type plus self link­ing num­ber was all that was needed to clas­si­fy trans­verse iso­topy classes of knots. Then Joan showed him 3-braids that ad­mit­ted a neg­at­ive flype, and Eli­ash­berg agreed with us that any 3-braid that ad­mits only a neg­at­ive flype had to have (two) dis­tinct trans­verse iso­topy classes with the same self link­ing num­ber; that is, such 3-braids were not trans­vers­ally simple. After es­tab­lish­ing the MT­WS, we were able to ad­apt our tech­no­logy to make this had in­to a proof [13].

A few ad­di­tion­al re­marks are of in­terest. First, in [10] Joan and Nancy Wrinkle showed that pos­it­ive sta­bil­iz­a­tions, ex­change moves and pos­it­ive braid pre­serving flypes were trans­verse iso­top­ies. (Neg­at­ive sta­bil­iz­a­tions al­ter the self link­ing num­ber so they can­not be trans­verse iso­top­ies.) Second, since there was a large com­munity of con­tact geo­met­ers work­ing with Flo­er ho­mo­logy in an ef­fort to pro­duce trans­verse and Le­gendri­an knot in­vari­ants, Joan thought it would be a good idea to pro­duce a table of low cross­ing 3-braids which were not trans­vers­ally simply [14]. Re­cent work of Len­hard Ng, Peter Oz­sváth and Dylan Thur­ston [e9] has es­tab­lished that cer­tain closed braids ad­mit­ting a neg­at­ive flype can be dis­tin­guished by such Flo­er ho­mo­logy in­vari­ants, but the 3-braids of this table are still res­ist­ant to such in­vari­ants.

In 2012 the valid­ity of the Jones’ con­jec­ture was fi­nally es­tab­lished, first by Dyn­nikov and Pra­so­lov [e12] us­ing fur­ther in­nov­a­tions of the sin­gu­lar fo­li­ation tech­no­logy in the arc present­a­tion set­ting, and then by Doug La­foun­tain and my­self [e13] us­ing fur­ther in­nov­a­tions of clasp an­nuli set­ting. Both ap­proaches use an Euler char­ac­ter­ist­ic for­mula com­ing from a sin­gu­lar fo­li­ation tiling.

I have heard it said that a suc­cess­ful ca­reer in math­em­at­ics is at least two good ideas. From her ini­tial land­mark book “Braids, links, and map­ping class groups”, to her work on the Jones’ poly­no­mi­al, to her work on the Vassiliev’s in­vari­ants, to her work with me on sin­gu­lar fo­li­ations, and more, I would say that a dis­tin­guished ca­reer comes from hav­ing a eye for where the math­em­at­ics is and where it should go.