by Allyn Jackson

Born in 1946 in Leningrad (now Saint Petersburg) into a Jewish family, Eliashberg earned his doctorate at Leningrad University under the direction of Vladimir Rokhlin in 1972. At that time the pendulum of Soviet antisemitism was on the upswing, narrowing Eliashberg’s job options to one institution, Syktyvkar State University, about 1000 miles northeast of Leningrad, in the remote Komi Republic. After eight years there, he applied to emigrate from the Soviet Union and was refused. His options narrowed further, and he spent eight years as a computer programmer in Leningrad.
He and his family finally received permission to emigrate in late
1987. He became a professor at Stanford University in 1989 and in
2004 was appointed to his current position as the Herald L. and
Caroline L. Ritch Professor of Mathematics.
Eliashberg’s honors include the Young Mathematician Prize of the Leningrad Mathematical Society (1973), the Oswald Veblen Prize of the American Mathematical Society (2001), the Heinz Hopf Prize (2013), the Crafoord Prize of the Royal Swedish Academy of Sciences (2016), the Wolf Prize (2020), and the BBVA Foundation Frontiers of Knowledge Award in Basic Sciences (2023). He was elected to the U.S. National Academy of Sciences in 2002 and to the American Academy of Arts and Sciences in 2012.
What follows is an edited version of an interview with Eliashberg that took place over three sessions in late 2023 and early 2024.
An after-the-war child

You were born in 1946, the year after World War II ended. Who were your parents, and what was their fate during the war?
As you said, I am an after-the-war child. I had two brothers. Both of them recently died; they were much older than me. One was 16 and a half years older, the other 13 and a half years older. My mother was trained as a pianist in Leningrad, in the conservatory. She wanted to have a career as a pianist, but she got married to my father, who was a chemical engineer. He worked in the pulp and paper industry. It was a really big enterprise. He was one of the main engineers, a deputy director responsible for the technological process. This was of course not in Leningrad but in many faraway places. So my mother had to follow him. At first she was carrying the piano with her, but that became quite difficult! Then my brothers were born, and then the war started. My father was for quite a while in occupied Leningrad during the war, during the blockade. Then he was sent to be the director of a pulp and paper plant in the Ural mountains area.
And your mother went with him?

My mother went with him. Then they returned to Leningrad, and I was born. Of course I don’t remember much about my first years. My father had a sister who lived with my grandmother. My aunt also worked in industry, actually far north, in Karelia, and I was sent there every summer.
Was that nice to go there in the summer?
Oh, it was always nice. I was five, six years old. I don’t remember much, only general impressions. There was a forest, and they taught me to collect mushrooms. Since that time I love mushroom collecting very much.
How did your mother feel about giving up her career?
What to do? She gave it up. She had a second career, after finishing at a foreign language institute. She taught English at a college. But she didn’t teach me, so I didn’t know any English! I went to school, just a local school in the area.

By that time, your brothers were grown.
My brothers were grown. My oldest brother, Gerasim, or Sima as we called him, became a very well known physicist. He moved to the place called Chernogolovka, near Moscow, where several physics institutes were started. One is the Landau Institute for Theoretical Physics. He was among the first three people who worked at the Landau Institute. He remained there and never left. He died two years ago. He was a member of the Russian Academy, so he was well established, a well known physicist and one of the founders of the theory of high temperature superconductivity. If you google “Eliashberg”, you get the Eliashberg Equation, which is not mine but his!
My second brother, Victor, was in my view an extremely brilliant person, superior to me and probably to my older brother as well. He was a very talented person who could do anything. But in his life, it happened that he always had to do something other than what he wanted to do. It was very difficult.
When my oldest brother was finishing university and Victor was going to study there, it was an extremely bad time. It was the late years of Stalin’s life, and there was the so-called “Doctor’s Case.” This was a manufactured campaign claiming that Jewish doctors were plotting to poison and kill Russia’s most important people. The campaign went on for several years. Because of this, my oldest brother Sima, although he graduated from Leningrad University and did something quite remarkable in his dissertation, was not able to get any kind of work as a scientist. He had to go to work in a chemical factory.

My second brother Victor was at that moment going to go to university. At that time in Russia there was a law that if you graduate from school with a medal, then you can automatically be accepted at any university you want. Both of my brothers graduated with medals. My oldest brother graduated before the time of the “Doctor’s Case”, so there was no problem, he could go to university. But my second brother Victor graduated in that bad period, so the university did not take him and he went instead to an electrical engineering institute in Leningrad. He became a really high-level engineer and worked on designing control systems. But he always was interested in other things.
He actually — well, I will stop because otherwise I will speak a whole hour about his ideas! I was really excited about what he tried to do. Unfortunately he was not able to do it because of his difficult life, but I am still dreaming that maybe at some time I can continue what he was doing.
What area was this in? Math?
No, his main interest was in the working of the human brain. He had a fantastic, absolutely unconventional theory about how it works.
Violin or mathematics?
Your brothers were so much older that in some sense you grew up as an only child.
In some sense yes, I was an only child. My mother
had this dream of realizing her musical aspiration in her children. So
she tried with my second brother to teach him, but then the war
started and it was not possible. I went to a musical school, learning
violin. And I was pretty seriously playing violin until I was maybe 14
years old. If you would have asked me before that time what I plan to
do in my life, I would say I would like to play violin. I was not a
fantastic violinist, but I think I played quite well. So I had this
inspiration.
Did you think at that time that maybe you would be in an orchestra?
Of course when you study violin you think that you will be a soloist! Who would dream to be in an orchestra?
True! But you thought you might make a career of the violin.
Of course, at this time, when I was 12, 13, I didn’t think in terms of a career.
How were your parents when you were in school? Were they strict? Did they make you do your homework? Or did they leave it to you because you liked school and you did well?
No. I did well. Nobody ever interfered in my school life!
Did you like mathematics from the start?
My oldest brother Sima moved out of the house and went to Chernogolovka, so I saw him only a few times a year. But Victor, or Vitya as we called him, was living at home, and he was my main inspiration. He got his PhD in control theory, but then he decided he wanted to do physics. And he was pretty successful in this. He learned physics essentially by himself. I was at the time 13 years old, and as he was learning physics, I was trying to do something along with him and was learning math.
Vitya also went to Chernogolovka, to a physics institute there — not the Landau Institute, a different one, in solid-state physics. Unfortunately for him, he was a fantastic engineer and was extremely good at any kind of instrumentation necessary for the physics experiments. People noticed this, and then that’s what he had to do. And that’s exactly what he didn’t want, because he really wanted to do physics research. So he got disillusioned. At that time he started thinking about the brain. Then he got married and returned to Leningrad and worked there.
Was that what got you into math, the contact with your brother about physics?
He had some influence — but no. At that time in the Soviet Union there was a system of mathematics olympiads. This was really broad, so that, for instance, all schools once a year were supposed to do some kind of olympiad. Each area of Leningrad had to have a local olympiad, and the winners were supposed to go to the city olympiad, and so on. It was a well structured system. I think it started from 6th grade. I went through this system of olympiads, and I did pretty well. I got second prize in my first city olympiad, without any real preparation.
There was also a system of mathematics circles, like mathematics clubs. A mathematician named Nina Mefantievna Mitrofanova1 looked at the list of olympiad winners and sent me a personal invitation to come to her math circle. It was at the Palace of Pioneers, which was a community center for children. She was running two math circles, one for people two years older than me, and the one I was in. This was a completely life-changing experience for me. She was a fantastic teacher. She then got married, to a mathematician, Yuri Burago.2 So I got to know him also.
What you did in the math circles was different from the mathematics you had in school.
Mathematics in school was in some sense not interesting at all. It was kind of standard mathematics. But the math circle was a completely different thing. I was there in 7th and 8th grades. Then for grades 9, 10, and 11 there was an experiment in the schools where every school specialized in some particular subject. I was still playing serious violin, and here I had a split moment. Either I need to go to a professional school for violin, or go to a school specializing in the sciences and mathematics. Some of the same people were participating in the science and mathematics school, like Nina Mitrofanova and Yuri Burago. They were not teaching there, but they were very much involved in the organization. And I decided at this moment to go in this mathematical direction.
What made you choose math over music?
It was a tough choice actually. But also, it was a somewhat romantic interest, because there was a girl I liked who was in the school!
You didn’t think mathematics was more practical than music?
No, no. Practicality was never a consideration. Actually, by this time, maybe there was a little bit of practicality. I had heard many stories about the music world. In order to make a career in music, it’s not sufficient to be a brilliant player. There is a lot of luck, and a lot of other things. I heard many stories about how some people succeeded, and others didn’t, and what they did to succeed. And somehow it wasn’t so pleasant.
Was that because of the strangeness of the Soviet system?
I think this is probably universal.
Universal in the performing arts?
In the performing arts, yes. Maybe in the Soviet Union it was even more so.
In the Soviet Union, there was a declared egalitarian principle, but in reality it was just the opposite, because there were people with privileges, and people without.
Of course, one thing that was universally understood was that you do not go into any kind of humanities stuff, anything social or literary, or philosophy — anything that has the taste of politics. Everything was politicized, but mathematics and physics were the least politicized. In this sense, music was probably far from ideal, but, again, I didn’t think in these terms.
Did you have good mathematics teachers in school?
Yeah, there were some good teachers there, but I didn’t interact with them. I didn’t have anything in this school that was interesting mathematically. I essentially escaped from the school. It was a three-year school, but I didn’t want to study for three years. I wanted to finish in two years. There was a group of us who started to go to Leningrad University, to the mathematics department, unofficially, to listen to some lectures. We wanted to leave school as early as we could! So we asked to take the exam to leave school, but we were not allowed. Then I just said, Okay, then I’ll leave. In the last half-year, I enrolled in a school where you have to come once or twice a week and just pass some tests. It was mainly for older people who wanted to get an education. They immediately understood that I knew quite a lot, so I was teaching mathematics to other students. I finished that school and then went to the math department at Leningrad University.
Becoming a university student

Did you have to pass an exam to be able to enter the university?
Yes. I passed the exam. The history of antisemitism in the Soviet Union went in waves. There was always underlying antisemitism, but sometimes it rose to the level of the state. I told you about the time when my brothers were studying. The year when I went to university, it was no problem for me to get in. The climate changed very rapidly, over the following three or four years, but at first it was pretty normal. I got into the university, and I very much liked my experience there and met a lot of fantastic people. My adviser was Rokhlin,3 who was a very remarkable mathematician. Maybe you know his story?
A little bit. He had a difficult time in the war, is that right?
Yes. He started in university in the 1930s. After the war started, he went as a volunteer to the front. He was captured by the Germans. Because he was Jewish, that was not good. But he was born in Baku, in Azerbaijan, and he managed to convince them that he was Azerbaijani, because he could speak fluent Azerbaijani. So he was not sent to a concentration camp but to some kind of military prisoners camp. He managed to escape, and then he was in Europe in different places, joining some resistance groups. Towards the end of the war, he managed to get back to the Soviet Union. And of course as soon as he got back, he was immediately imprisoned and sent to a camp, because everybody who had been captured by the Germans was not reliable and had to be sent to a camp! Before the war he had already been quite brilliant mathematically. He had worked with many mathematicians, so he was known. So some of them managed to get him out of the camp, and he got back to Moscow. But of course he couldn’t find any job. Pontryagin,4 who was one of the people who had helped him get out of the camp, took him on as his helper. Pontryagin was blind, so he had a special position of helper.
So Rokhlin was working at the Steklov Institute, and he got his second
doctoral degree, similar to the Habilitation in Germany. Then
he was fired because his qualifications did not correspond to his
position as helper! He couldn’t find a job in Moscow, so he worked at
places that were an hour or two away by train. But still he ran a
seminar on ergodic theory in Moscow, which was extremely
important. People like
Sinai,5
Arnold,6
and others went to this seminar, and
later they said it had been really important for them.
At some point, the mathematician Alexandrov7 became rector of Leningrad University. He personally invited Rokhlin to Leningrad. So Rokhlin came maybe three years before I entered. Immediately he got fantastic students. For instance among his first students was Gromov.8
That’s impressive that Rokhlin went through so much in the war but then had the energy to keep his mathematics going, even in a difficult work situation.
Yes — but maybe if you are relaxed you are not so motivated. It depends on the person, right? For some people, it’s like the difficulty helps them to do better. But of course, you are perfectly right, it’s remarkable.
So Rokhlin had a seminar in Leningrad, where I started to participate, and a lot of fantastic people were there. I met Gromov there. Gromov is three years older than I am, but four years ahead in studying because he started early. So I didn’t talk to him at first, but he was already quite famous, so I had heard of him.
My first serious interaction with Gromov was the following. We had five years in university, and after the fourth year, Rokhlin gave me a problem. I was thinking about this problem in the summer, and I solved it. Then I started to think of something that was in some sense an opposite question, a reverse question. I understood how to do that too, and I was very excited. In September, I came to Rokhlin and started telling him what I had done. And he said, “Well, it seems very interesting. Gromov just told me something very similar. You should go talk to him.”
That was my first serious talk with Gromov. From that moment, all my mathematical guidance was mostly from Gromov. I talked with Rokhlin of course, but with Gromov much more.
What was the problem that Rokhlin gave you?
Rokhlin and Gromov were at that time writing a survey on isometric embeddings for the Russian journal called Uspekhi Matematicheskikh Nauk. This journal was translated as Russian Mathematical Surveys.
In the theory of isometric embeddings, when you want to construct such an embedding, you usually start with a so-called free map. If you have a curve, there is a tangent line, but also there is a plane that approximates the curve in the best way. This is the plane spanned by the velocity vector and the acceleration vector — the first and second derivatives. It’s called the osculating plane. For a manifold of higher dimension, for instance for a surface in higher-dimensional space, you can look at the osculating space, which is the space spanned by all first and second derivative vectors. For a 2-dimensional surface, the osculating space in principle should have the maximal dimension of 5, because there are two vectors of the first derivative, and three vectors of the second derivative.
A map, or an embedding, is called free if at every point the osculating space has maximal possible dimension, which is 5 in the case of a surface. In the case of a curve with an inflection point, where the first and second derivatives align, they span a line instead of a plane. That’s a bad point — the embedding is not free. The picture is similar in higher dimensions.
One question is, What is the minimal dimension of, say, Euclidean space where you can map a manifold freely? When Gromov and Rokhlin mentioned this in their survey, they wanted some kind of obstruction, some kind of negative result — a way to say for which manifolds it’s not possible to embed them in such-and-such dimension.
So I thought about this, and it was actually not a hard question. I understood it pretty fast and computed some examples. But then I started to think about the opposite question. There are algebraic obstructions, in terms of the topological characteristics of the manifold. Suppose those obstructions vanish. Question: Can you find such free embeddings?
At that time, this was a fashionable question, because there was the Smale–Hirsch immersion theory, and the answer they give for existence of immersions was similar. So this was a natural generalization, from my point of view. And I realized how to do this. In modern terms, I proved the h-principle in this case! Though it was not called the h-principle at the time.
This was 1968, when Gromov wrote his famous paper9 from which the theory of the h-principle essentially developed. He was thinking about a similar question and had found a way of solving that question that was very close to my idea. It was essentially the same procedure. He told me, “Okay, great, let’s think about all questions we can solve by this method.” That essentially started our collaboration. We wrote maybe four papers at that time together. It was a pretty productive time.
Rigid and flexible mathematics
What makes Gromov such a powerful mathematician?
It’s extremely difficult to say. Who knows what makes great people great? But what I see as quite remarkable is the way Gromov thinks and works. He always is trying to uncover the deeper mechanism behind why something is true. I’ll give you an example.
Before I started talking seriously to Gromov, Rokhlin organized a
seminar for us youngsters who had just started. He asked a graduate
student to run the seminar, which really was a fantastic experience
for me. Not long before this, the Smale–Hirsch immersion theory work
had appeared. I was asked to give a talk about it in the seminar. So I
read all the papers, I thought I understood them, and I gave a
talk. But several years later, when I started to interact with Misha
Gromov, we talked about this, and then I realized I really didn’t
understand anything!
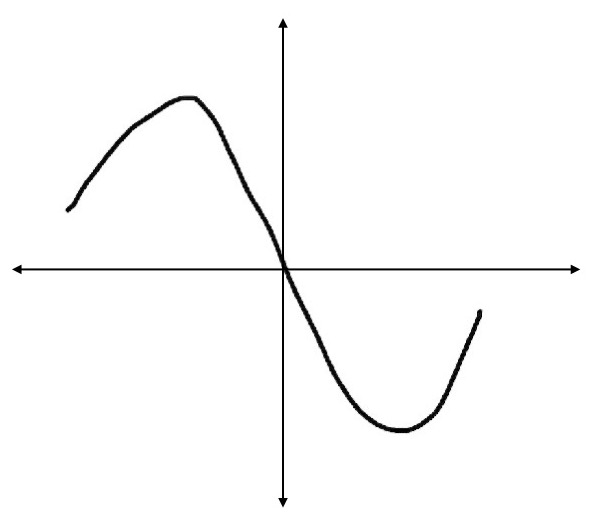
There is a very simple geometric mechanism showing why immersion theory works. Suppose you have a function increasing near the endpoints of an interval, and you ask, is it possible to extend the function over the whole interval without a critical point? If the value of the function at the left endpoint is smaller than at the right endpoint, then the answer is yes. Otherwise, it is impossible. But as soon as you allow two critical points, the picture becomes extremely flexible (see Figure 1).
You can always extend inside the interval with precisely two critical
points; you don’t need to create more. This picture is the key thing
that makes the whole Smale–Hirsch immersion theory work. Everything
is based on this. That’s what Gromov observed. You could say that
his PhD dissertation is an explanation of this simple picture with the
two critical points. He transformed it into a fantastically powerful
tool.
Here is another example. Gromov was also thinking about the work of John Nash on \( C^1 \) isometric embeddings. An isometric embedding is a way to bend surfaces without distorting distances. For example, if you take a sheet of paper and bend it, that’s like an isometric embedding of a plane in the space. Suppose now you have a sphere of radius 1. Without disturbing distances, can you squeeze it into a very small ball?
There was a discovery of Nash that this is indeed possible, but only if the crumpling is \( C^1 \) smooth — the second derivative does not exist. If you try to do this in such a way that the second derivative exists, so that, besides length you can also measure curvature, then it is easy to prove that this sphere cannot be crumpled in this way. It’s really rigid. But if you don’t care about curvature, so that the embedding is only \( C^1 \) smooth, then you can do that. This is the \( C^1 \) isometric embedding theorem, which was proved by Nash and then improved by Kuiper. Many people knew about this, but Gromov really understood what it means. He transformed it into a method, now called convex integration, which really unwinds what Nash was doing.
I think what makes Gromov different from most of us is that for him, understanding means something completely different from what it means to other people. For him it means understanding some basic mechanism behind a phenomenon. Suddenly it turns out that this mechanism is much more powerful than its use in that particular phenomenon. Then a whole new area might open up.
So Gromov is able to see the simple, basic things going on in the background.
Maybe they are not so simple, but you see, there should not be such a thing as a difficult mathematical theorem, right? If you have a difficult theorem, that means that the proof is not properly understood. It’s not structured correctly. A proof could be long, but we need to understand well what is going on at each step.

You and Gromov developed the philosophy of “soft” and “hard” mathematics. Can you tell me about this?
I prefer the terms “flexible” and “rigid”, because this is not about difficulty of problems. My viewpoint on all this changed a lot over the years. Now I see it as nothing special.
What are mathematicians doing? They are inventing some worlds, and then they are exploring these worlds. For example, say you want to understand geometry in four dimensions. In three dimensions, we think we understand more because we have eyes, we have some experience with our hands. But not in four dimensions. There we have to invent tools for working and visualizing. Like the idea of Morse theory. You take a function on a 4-dimensional object and consider its level sets, which are 3-dimensional, and then you analyze how they bifurcate.
Every mathematician lives in some mathematical world, which he tries to explore. You need to understand what is possible in this world and what is prohibited. So for instance, you have a surface and you want to construct a vector field on it, and you don’t want this vector field to have zeros. If you take a 2-dimensional sphere, you realize that on a sphere, this is not possible. If you are a very stubborn person, you would try and try and try, but maybe at some moment you should stop and think, and then prove that it is not possible.
Or suppose you are trying to construct a gradient vector field on a torus, without zeros. This is also not possible, while a nongradient vector field without zeros does exist! It’s not possible because every function on a closed manifold must have a maximum and minimum. You realize that a maximum and minimum are necessary, but ask, Can we do it so that there are no other critical points? In topology there is something called the Morse inequalities, which say no, this is not always possible. It depends on the topology. If this were possible, then our manifold would be homeomorphic to a sphere.
There are always these attempts to construct things in mathematics, and then something prohibits certain constructions. So in some areas, it is extremely difficult to construct anything! Almost everything crashes! In topology, it’s a more flexible world, there are a lot of interesting constructions you can do. At the same time, there is this rigidity, called topological invariants, which prohibit us from performing certain tasks. What I call flexible mathematics and rigid mathematics are precisely these two aspects. In one we are trying to take our constructions as far as possible. Then in another we are looking for the constraints on our constructions and trying to understand what is impossible.
So this is rigid mathematics and flexible mathematics. An ideal mathematical field is when these two aspects come into as close proximity as possible. That would mean that we know how to live there. We know what we can do and what we should not try to do.
Strong personalities are dangerous
You got your PhD in 1972, with Rokhlin as your adviser. Yuri Matiyasevich10 was also at Leningrad University at the time. Did you know him then?
I told you about the math circle of Nina Mitrofanova. This was an extremely strong group of young people, and Matiyasevich was among them. So yes, I know him. He is my friend, we grew up together.
He solved Hilbert’s Tenth Problem in 1970. Was this big news in the mathematics department in Leningrad?
Yeah, it was of course really big news.
Several other people in Leningrad were extremely good mathematicians. An important figure was the older Faddeev, not Ludwig Faddeev,11 but his father, Dmitry Konstantinovich Faddeev.12 He was an algebraist and taught one of the courses I took. He was a very interesting person.
The mathematics department was divided into “chairs” according to mathematical areas. So there was a chair in algebra, in topology, and also in mathematical physics. In mathematical physics there were two remarkable women mathematicians, Olga Ladyzhenskaya13 and Nina Uraltseva.14 Both of them were — and Uraltseva still is — wonderful people and great mathematicians. Another was Mikhail Solomyak,15 who emigrated later and was working at the Weizmann Institute.
On the analysis chair were several mathematicians who were very important for me. One of them was Viktor Petrovich Havin.16 He was in complex analysis, and a lot of high profile people went through his school — not necessarily his students, but students of his students, including some Fields Medalists, like Stas Smirnov.17 Another very remarkable person was Anatoly Vershik,18 who recently passed away.
But at the time I was there, the university administration didn’t like bright people. It was never stated, but my impression was they preferred to have more mediocre people. The strong people are always dangerous because they have their own opinions! It is much more difficult to manipulate them. So Gromov never was able to get any reasonable position in Leningrad University. He was so obviously great that, when he graduated, they had to give him a university position. But it was ridiculous, the lowest paid position. If you went to a metro station, and you saw an advertisement for a cleaner in the metro, then the salary was much bigger than what was paid to Gromov! Really ridiculous.
Was that also because he is Jewish?
No — okay, he is half Jewish. I doubt it, but it may have played a role. But I would say the more important reason was that he was too good to have — too dangerous to have such a great person!
Also, Rokhlin had to retire quite early from the university. Officially there was a five-year contract that was automatically renewed, and it was understood that it would be renewed indefinitely. There was a pension age, which for men at that time was 60 years. Professors at the university normally would stay until they are dead or close it! But not Rokhlin. They pushed him out as soon as he was 60.
Was there a lot of competition between Moscow and Leningrad as mathematical centers?
There was no competition, because of course Moscow won 100 percent. There were absolutely incomparable resources there. Interaction with the West was mostly in Moscow. In later years, some people were coming to Leningrad, but that was exceptional. There was no comparison between the level of intensity of mathematical life in Moscow and Leningrad. Of course, Leningrad was still a good place compared to most.
A lot of people in the West felt there was a special spirit in the mathematical life in the USSR. Do you feel that’s true?
There was an absolutely remarkable number of fantastic mathematicians, mainly in Moscow. Of course Gelfand19 was a magnet, and so was his seminar, which he created. No question about this. There was a group of really amazing mathematicians, like Novikov,20 Arnold, Kirillov,21 Sinai, Fuchs,22 Manin23 — a fantastic group of mathematicians, more or less of the same age. And as I said, Rokhlin played some role in the upbringing of this group, because most of them went through his seminar. There was an extremely good mathematician who was not so great a person, Shafarevich.24 Then of course Kolmogorov25 and the older generation played an enormous role. So there was no question, there was a brilliant group of mathematicians in Moscow University. Anosov26 should be in there too — of course, this list should go on and on. It is a far from an exhaustive list.
What I didn’t like was that in the Soviet Union, on every level, they were recreating the structure of the whole Soviet state, in miniature. There were leaders who had “schools”, and you needed to belong to a school. Some of these schools were great, especially in Moscow and Leningrad. But some were quite mediocre and self-reproducing. Of course, this exists in the West as well. One of the great schools was around Gelfand and his famous seminar. The Gelfand seminar had enormous influence on the development of mathematics not only in the USSR but worldwide. But I also know a very good mathematician for whom participation in Gelfand seminar was a hurtful experience that he remembered for a long time.

I never participated in the Gelfand seminar in Moscow. Much later, in the mid-1990s, I was visiting the IHES [Institut des Hautes Etudes Scientifiques] at Bures-sur-Yvette. The first person I met when I arrived there was Gelfand. He was seemingly glad to see me, took me to his office, and asked me to tell him what I was currently doing. I began to talk, and he almost immediately fell asleep. I stopped and waited for him to wake up. “You never learned how to properly explain things”, Gelfand told me when he opened his eyes. He invited me to talk at his seminar at the IHES, which I did. I think the seminar went quite well, though maybe it was not so pleasant for Ofer Gabber, whom Gelfand constantly called to the blackboard to prove what I claimed to be true.
Another remarkable and very influential figure in Soviet mathematics was Arnold. In addition to Rokhlin and Gromov, I was very much influenced by Arnold. He was in Moscow, not Leningrad, but starting at some point I interacted with him almost every time I was in Moscow. I am not his student, but I am kind of on the periphery of his world.
The e-Machine: Modeling the human brain
You mentioned your brother Victor’s ideas about the human brain. You actually worked with him on this.27 Can you tell me briefly about it?
It’s extremely difficult to describe in ten minutes! But let me try. He and I shared the point of view that what the brain is doing is some kind of computational process, though of a different kind from a conventional computer. Still, we are universal computers in a sense. And there is a simple theorem saying that you cannot be a universal computer if you don’t have what is called read-write memory. This means you have a memory storage, where you not only can store things, but also can reuse the same memory position for new information. Conventional computer architecture uses a separate processor, which can perform some operations. All conventional computational processes look like this. We take something from memory, send it to the processor, perform an operation, write back to the memory, etc. In order to do anything serious in real time, we need to do these things very fast.
But nobody has ever observed anything like these kinds of processes in the brain. According to currently accepted models of memory, information in the brain is encoded in connectivity of synapses — the way the neurons attach to each other. This synaptic memory cannot go very fast because it’s based on chemical processes. And nobody has ever observed in the brain something like flows of information going from memory to processor and back, like in a computer.
But as I said, there is a mathematical theorem saying that if a system doesn’t have read-write memory, or something that can simulate read-write memory, then it does not have the power of a universal computer. Therefore the question Victor asked is, What does the brain have instead of read-write memory? We can play chess, we can perform extremely complicated algorithms. But whatever it is that carries out those algorithms cannot be the conventional kind of architecture. So what is it?
He came up with a proposal, which sounded to me extremely probable, for how this can be done. According to him, computations are performed in the space of functions of the write-only, or “long-term,” memory. Roughly speaking, his proposal is the following; it’s not a model of the brain but a metaphor for an elementary block of which our brain is built.
Suppose you have some kind of memory storage, like a tape, where you can record information. You have information coming to your eye or ear or whichever sense. At discrete times there is some multidimensional vector of information coming in. Let’s do a naive thing and suppose that you just record incoming information successively, like on a tape recorder, so information that comes at time \( t \) you record at position \( t \), the first available position.
Suppose that at the same time the information is being recorded, there is a very simple mechanism that compares how this vector that comes at time \( t \) relates to what was recorded before. It might compute a very simple function, for instance, the scalar product. You have at every moment this function, so you can identify the stored signal most similar to the one that just came in. This works like associative memory, so that there is an access mechanism by analogy, by association.
But this would be a very stupid machine if it just repeated something
that was already prerecorded. That would be absolutely not
interesting. So let’s suppose there exists the following additional
mechanism, which in neuroscience is called “residual excitation”.
Suppose the function is actually some kind of physical field, for
example a potential. It was created at time \( t \). At time \( t + 1 \), it
does not disappear but instead starts to decay. But also at time
\( t + 1 \), a new signal comes. So this function depends not only on
what came at this moment, but also on what came before for a certain
period of time, because of the residual excitation. This would, for
example, allow you not only to recognize letters, individual signals,
but to recognize temporal sequences, to recognize words. Victor
called this the “e-machine”, where e stands for excitation.
Both input and output are divided into two kinds of signals, sensory and motor. We have information from the outside world, from our senses, but we also have information from inside ourselves. For instance, you tell me something, and I move my hand. Whatever I did to move my hand, a certain signal was sent to my muscles in order to do this. That signal is also being recorded, and it is information to which I have access. Furthermore, one can consider hierarchical systems built of e-machines, where the “sensory” input for e-machines of a higher level is coming from e-machines on a lower level and their “motor reaction” control machines on the lower level.
I am describing a computer architecture that is a universal architecture. So in principle whatever it’s possible to do on a computer, it’s possible to do in this architecture and vice versa. But certain algorithms that are simple and natural, or native, for this type of architecture require enormous work to be programmed on regular computers. They are not natural there. This system is much more like us. It is programmed by experience.
Computers have the property that they are extremely sensitive to programming. If you write a program with errors, then it just does not work. Even if you create some kind of tolerance so that it is stable with respect to some small error, still, it’s extremely sensitive. You have to be very precise in the instructions for it to work.
But we humans — imagine how much garbage has been put into our heads during our lifetime! Despite the garbage — which you can call indoctrination — what we do (or at least what some of us do) is rational to a large degree. If most of our information is not garbage, then still we are able to function. The system I described has this capability.
One job option, in faraway Syktyvkar
Let’s go back to Arnold. Can you tell me about your interactions with him?
I first spoke at Arnold’s seminar in Moscow in spring 1969 during my last undergraduate year. Later on, I gave several talks at this seminar. Mostly they went quite well, but once it was a disaster. It was sometime in the fall of 1984. I came to Moscow for a few days and called Arnold. As usual, he asked if I want to give a talk at his seminar. At that time Misha Gromov was finishing his seminal paper where he introduced the technique of holomorphic curves in symplectic geometry, which brought about a revolution in this subject. Just before I came to Moscow, I received from Gromov a preliminary draft of his paper. So I told Arnold that I could talk about Gromov’s work. For some reason, during my talk Arnold was extremely aggressive. After I had talked for 10 minutes, he interrupted me and said that before going on I should say what is the main idea. In my view, in that paper there are several equally important ideas. So I tried to start from different sides, but each time Arnold was not satisfied and didn’t let me speak before I told him what is the main idea. Finally at some point I said something — which in my view is an important but definitely not the main idea! — that suddenly satisfied him, and he said, “Why did you waste almost two hours of our time and couldn’t start from this point at the very beginning?”
In Russia, for a PhD dissertation, there are two official “opponents,” as they are called — a referee, who is supposed to read the dissertation, and the adviser. When you have your PhD defense, they are supposed to come and say what they think about your work. Arnold was one of the opponents (the second one was Alexei Chernavsky28 ) for my PhD dissertation. He came on the night train from Moscow to Leningrad, and I met him about 5 a.m. at the train station. I was bringing him to my home to talk, and on the way there he told me he did not understand a lemma in my dissertation. I had written that this lemma is obvious. He said that first of all, he does not believe that it is obvious, and second, he believes that it’s just wrong.
We came to my home, and Arnold was extremely sleepy, so he decided to sleep for a couple of hours. While he slept, I was thinking about how to explain this lemma to him. He woke up, and we talked for an hour, and then he said, “Now I believe this is true, but still I don’t see that you have a proof.” At my dissertation defense he didn’t say anything about this lemma. But then about a year later, he sent me a paper he had written, with a note saying, “Now we have proof of your obvious lemma!” The paper had a result that implied my lemma. I still think it was obvious, but — !
After that, each time I was in Moscow, which was not that often, I tried to see him. When I was in Syktyvkar,29 he came there to participate in a conference that I organized, so I interacted with him there.
You went to Syktyvkar right after your PhD. Can you tell me how you ended up going there?
At the time I finished my PhD, the antisemitic situation was pretty bad again. When I entered the university, it was not bad, but by the time I finished and was supposed to go to graduate school, it was bad again. For instance, there are entrance examinations for graduate school. One of the exams was about political things — communist party history, or scientific communism. They tried extremely hard to fail me on that exam. I didn’t fail only because there was a representative of the mathematics department on the exam committee. Nina Nikolaevna Uraltseva — the professor of mathematical physics who I mentioned before — was on the committee, and she didn’t let them fail me. So I got the lowest passing grade, but they passed me.
I was admitted to graduate school, but I had to sign a paper saying that, after my PhD, I agree to go anywhere they would send me. The Leningrad Branch of the Steklov Institute really wanted to take me for a job there after my PhD. This was a fantastic place to be. The director of this institute was Grigorii Ivanovich Petrashen.30 He was an extremely good person and a good mathematician. He tried really hard to hire me. But this was a branch of the Steklov Institute, so he needed to get approval of the director of the main institute in Moscow, who was Vinogradov.31 And Vinogradov was a very famous antisemite.
The rule established by Vinogradov said that the Leningrad branch is allowed to decide on its own to hire anybody they want — except Jews. Any Jewish hire was supposed to be approved personally by Vinogradov. So Petrashen would tell me, “Of course I will get his permission, but I need to find the appropriate moment. Next month I go to Moscow, and I will bring this up.” And then he would return and say, “The moment was not appropriate so I didn’t bring it up.” It got extremely close to the time of my graduation, so there was no time to wait, and then he finally did talk to Vinogradov. When Petrashen returned to Leningrad, I talked to his secretary. It turned out that he had entered a psychiatric clinic after his discussion with Vinogradov! I very much hope that it was not because of me, but anyway Petrashen had had some kind of nervous breakdown.
Vinogradov had said no. Then I didn’t have anywhere I could go. At this time, a new university was being organized in Syktyvkar. Because it was new, Leningrad University was assigned as a “parent” organization, to help them get started. The rector of the new university came to Leningrad, and she had a carte blanche to choose any new PhD she wanted. And she chose me, because I was extremely convenient to hire. Students were usually defending their PhD dissertations in the fall, and I had already defended in May. So I was ready to go immediately, before the academic year started.

So I went to Syktyvkar. It was I would say an interesting experience. I was there for eight years, and I liked my time in Syktyvkar. It was interesting, it was a new place, and they really organized this university from scratch. Mostly they hired good young people from Leningrad and Moscow. There was a very nice atmosphere at the beginning. They were able to give me an apartment, which was very good, because in Leningrad getting your own apartment was difficult. But the great things in Syktyvkar became not so great because, as usual, bureaucracy takes over. The atmosphere became not as exciting.
How was it mathematically for you there?
Mathematically for me it was difficult, because I had a lot of teaching. I started out teaching 18 hours per week, which was quite a lot. Then they made me a chair — there was a department of mathematics and physics together, and I was chair of one mathematical part. I didn’t have much time. But it was okay, and I did some good work there.
Emigration: An extremely difficult decision
Were you working on the Arnold Conjecture in Syktyvkar?
I was working on the Arnold Conjecture already at the beginning of my time in Syktyvkar. When I was finishing my dissertation, I was still collaborating with Gromov a lot.
By the way, Gromov left the USSR in 1974. In fact, at some point there was a chance that, instead of going to Stony Brook, he would come to Syktyvkar! As I told you, Gromov had this extremely badly paid position in Leningrad University. A good thing about this position was that he didn’t have many obligations, so he could just do mathematics. But it was not really a reasonably paid job. They made a condition for his promotion that he would spend some time in Syktyvkar. After that he could go back to Leningrad. My feeling was that he was really considering this. In Leningrad he didn’t really have any place to live — he was renting a room with his wife. He asked Leningrad University if they could give him a place to store his stuff while he worked in Syktyvkar. But of course nobody ever gave him anything. I don’t know if it was for this reason or another reason, but he decided against Syktyvkar. But he did visit Syktyvkar and talked to people there.
That was in 1972. I think at that time, he decided he would leave the USSR. So he left Leningrad University and worked at various places, and then eventually emigrated.
Did you think about emigrating at that time?
No, I didn’t think about it. In 1975, my brother and his family and our mother decided to emigrate. They left in December 1975. Eventually my brother found a job in California, so by 1976 they were in Palo Alto.
What about your father?
My father had already died by then. He died in an accident in 1968.
Why did you not think about also going to the US at that time?
At that moment, I didn’t want to go. You know, that was an extremely difficult decision. At that time it looked like you would not only go through the humiliation and everything, but you were also cutting forever any ties with friends — with anybody.
But then, at some moment people in Syktyvkar learned that my relatives were abroad, and that became not such a great thing.
What happened when they found that out?
For instance, my position as chair became very weak. Being a chair, your main role is to protect the department from all the stupid things coming from the administration. I remember that once I said something against what the rector was proposing, and she said to the others, “Why do you listen to Eliashberg? He has a villa waiting for him in California!” Various things like that happened.
Gromov had left in 1974, which was a blow, because, besides being
mathematically an important person for me, he was my friend. Towards
1978, I had to make a decision about emigrating. It was an extremely
difficult decision, especially at that time. But as more things
accumulate, you feel that it’s not really possible to continue
anymore.
What did your wife think about going or staying? You were married at this time, right?
Yes, we were married and had two children at this time. My wife Ada was supportive of course, but the one thing that she knew for sure was that she did not want for us to remain forever in Syktyvkar. But clearly there was absolutely no possibility for me to return and get a decent job in Leningrad. If I had not been married and had been alone, maybe I would still be in Syktyvkar. Women are moving progress!
So we decided to leave. It was technically almost impossible to apply
for emigration from Syktyvkar. So we came back to Leningrad with the
idea of applying for emigration from there. We applied sometime
around the end of summer 1979. But then in December that year, the
USSR invaded Afghanistan, and the war started. Then it was clear that
the situation had become such that we would not get permission, and
indeed in about a month we got refused.

After that, it was pretty bad, because of course I couldn’t find a job. I worked as a substitute teacher in middle school, which was pretty tough. Then one of my friends helped me to get a job doing computer programming. He essentially put his career on the line to help me. In the place where he worked, he was the main person on whom everything depended. They couldn’t let him go. And he said if they don’t hire me, he is leaving. So they hired me. I worked there until I managed to get permission to emigrate, in 1987.
That was mainly thanks to my brother Victor, who was writing to congressmen, to everybody he could think of, in America. I was invited to speak at the International Congress of Mathematicians in 1986 in Berkeley. Of course the authorities didn’t let me go, but my brother and his family and friends organized a petition to free me. I still have the petition, with almost 1500 signatures.

They collected signatures during the ICM?
Yes. During the ICM they put a table in front of Evans Hall32 and collected signatures. They also made pins on which it was written, “Let Yakov Eliashberg Go!” When I came to the US, I got as a present maybe 10 such pins from various mathematicians!
My brother collected the signatures and gave the petition to a congressman, and this helped. The congressman went to Moscow and talked to some people there. The Soviet Union still was intact then, in 1987. People were not leaving. The Soviet Union collapsed in 1991. But in 1987, 1988, it was difficult to leave.
You couldn’t go to the ICM in Berkeley, so John Mather gave your talk.
I asked that Misha Gromov give my talk, because of course he knew this stuff inside and out. A person I have mixed feelings about is Ludwig Faddeev. He died some years ago. He was of course a very good mathematical physicist, and I knew him for many years. I think he was the chair of the Russian delegation for the Berkeley ICM. When I got the invitation to speak, I came to him — he was in Leningrad. He said of course there is no chance I can get permission to go to the ICM, but he offered to take my lecture and give it to someone there to read. I asked him to give it Gromov. But Faddeev didn’t do that, because Gromov was seen as a bad person, from the Russian point of view. He was politically incorrect!
Exploring mathematical worlds
Let me ask a different kind of question. What goes on in your brain when you do mathematics? Do you see geometric pictures, or do you envision processes, or do you think about calculations? What goes on in your brain?
I never analyzed my own brain. In mathematics, it’s like you are a world explorer. You are exploring a world, and maybe this world is related to our real world, but it’s a subworld. For instance I am doing symplectic geometry, which has some rules, and I try to understand what is possible in that world, constrained by these rules. But it’s extremely difficult to concentrate and think linearly in this world. You go into this world, but there are a lot of outside factors that can disturb you, and your thought goes completely to the wrong place. You need some discipline to return back to that world.
There are distractions?
It’s not necessarily outside distractions. It might even be distraction from your own brain. Whenever I have made progress in my mathematical thinking, it was because I was able to think for a sufficiently long time. I am traveling in this world, and I need to walk there a sufficiently long time — at least for a few minutes — without getting out in between.
So you need enough time to immerse yourself in that world.
And you come to the place where you wanted to go, but then suddenly something happens and your brain moves you completely wrong. Then you need to force yourself, no, come back, continue, try to see what’s there.
So it’s seeing, it’s geometric? Or are you feeling around, it’s something tactile?
I cannot say. It’s a little bit geometric. Some people are able to see much more. It’s difficult to say.
I can tell you an interesting story that Misha Gromov told me. He used to be a smoker, and several times he tried to quit but again started smoking. The main thing that irritated him was that, before he stopped smoking, he always had in his brain a blackboard, and he was writing on the blackboard. But when he stopped smoking, this blackboard disappeared. He didn’t have anything to write on! I kind of understand this. I don’t have any blackboard, but there is something in this spirit.
If you talk to another mathematician about the things you are thinking about, do you get the impression that that person is in the same mathematical world as you were, when you were thinking about the topic? Or does it seem like they are in a different but maybe similar place?
People have different ways of thinking. I think that’s the most exciting thing, that people collaborate, and they have different ways of thinking. You can say, “This is clear,” and then somebody else says, “It’s completely unclear. Why is this true?” You had in your brain a certain point of view, and from this point of view something indeed was pretty clear. But then when you approach it from a different point of view, then this maybe is not clear at all.
In the world you are exploring, there are objects there, and you can look at them from very different perspectives. So it’s natural that different people have different views. Of course, there are people with whom you feel more affinity in the way they think. But the best collaborators are those who think differently.
A paper never accepted, never withdrawn
What were you working on mathematically when you were still in the USSR?
When I got my PhD, I was working with Gromov on all this stuff about the h-principle, the flexible mathematics that I mentioned before. I wrote several papers, with and without Gromov. I learned about the Arnold Conjecture from Gromov. We both thought it’s unlikely to be true. We thought maybe it’s true in dimension 2 as a special case, but not in high dimensions. I had some kind of argument that almost proved that indeed it’s not true. But then I realized that I was wrong, and I tried to fix the proof. Of course I couldn’t fix it, and then I started to think that maybe it is true. And I started to think about what is now called symplectic rigidity.

In Syktyvkar, I was trying to prove the Arnold Conjecture for surfaces, and I eventually proved it in 1978. I sent the paper to the journal Functional Analysis and its Applications, where Gelfand was the main editor. Arnold was a deputy editor, and I think he essentially was running the journal. From time to time I was coming to Moscow from Syktyvkar and talking to one person I knew, Dmitry Fuchs. He is older than me but I consider him my friend. Usually when I came to Moscow I stayed in his home. He organized a small seminar to go through my proof. After I sent the paper to the journal, I came to Moscow, and Fuchs told me that Askold (Asik) Khovanskii,33 a former student of Arnold whom I knew very well, wanted to talk to me. So I called Asik, and he said, “Well it’s great that you are here, because I am refereeing your paper, and I don’t understand something.” I explained it to him and, I think, convinced him. Then, some time after that, I got an extremely angry letter from Arnold, who said that I destroyed his referee —
Because you spoke to him.
— because the referee spoke to me. Therefore Arnold had to start the refereeing process from scratch. There is some truth in this. Arnold explained that the goal of the referee is not only to check whether the proof is correct or not but also if it could be understood from what is written. If I have to explain it to the referee, then that means it’s not possible to understand the proof as written.
This happened around the time when I applied for emigration. Of course this became known by people on the editorial board, and they were extremely afraid that publishing a paper of such a bad person like me could be harmful for the journal.
It’s staggering to think that that happened.
Yeah. Gelfand felt that his main goal was to protect the journal. If someone said that the journal had published a paper by a person who applied for emigration, that would be bad for the journal.
My paper is still at this journal. It was never rejected because they probably didn’t have a mathematical reason for rejection. But it was not accepted either. Somebody — I forgot who — called me from the editorial board and asked me to withdraw the paper, because the editorial board had made a decision to not publish papers of people who may have a possibility to publish in more widely readable journals! But I refused to withdraw it. So that means it’s still there.
It never got published?
It’s never been published. In the Soviet Union there was a place called VINITI,34 which was an organization that published Referativnyi Zhurnal, the Russian analog of Math Reviews and Zentralblatt. You could send a paper to VINITI, and it would not be published but it would be reviewed and the abstract would appear in Referativnyi Zhurnal. Then if somebody was interested, they could write to the author and request the text. So I sent the paper there. In the Soviet Union this was considered as some kind of formal publication.
Did other people prove the same thing that you had in that paper?
Yes, later on. It was between the end of 1978 and 1979 that I sent this paper to VINITI. Then many things happened. In 1983, there was a paper by Conley and Zehnder35 that proved the case of tori. I had proved it for all surfaces, but they proved it for tori of any dimension, so that is a much stronger result. Gromov wrote his famous paper36 about holomorphic curves in 1985, which implied some of what I had proved. And then Floer, also around 1985, wrote a paper37 where a proof of the same result appeared. But my proof is different from all other currently known proofs, so I think it still has its value.
Everything goes back to Poincaré
Can you say more about the Arnold Conjecture — what it is, and why you and Gromov thought it might not be true?
Everything goes back to Poincaré. Poincaré in 1912 wrote an extremely dramatic paper.38 It says, “Well, here is a question I have been looking at for a long, long time, and I have considered many special cases. I am convinced this is true but I wasn’t able to find a general proof. But I am already old, so I decided to write this incomplete paper.” Actually he was not old, he was 56, but he was sick, and he died a few months later.
The problem Poincaré wrote about was a geometric problem to which he came by analyzing periodic orbits in the so-called restricted 3-body problem. This is the case of the 3-body problem when one of the bodies is small and the effect of its gravity on the motion of two other bodies can be ignored. An example is the case of a satellite moving in the gravity of the earth and moon. Poincaré reduced this problem to the question of finding fixed points of an area-preserving transformation of the annulus. Here preservation of area means that, while a subdomain in the annulus might be mapped onto something very complicated, the area of its image remains the same. Poincaré claimed that if, in addition, such a transformation rotates the boundary circles in opposite directions, then it must have at least two fixed points.
This became known as the “last geometric theorem of Poincaré”. It was actually proved pretty quickly after he died, by George David Birkhoff in 1913.39 Poincaré obviously thought of this as a special case of something very general but while Birkhoff’s proof was very clever, it was very specific to this particular example. Somehow, it was a dead end. Not much followed until Arnold, around 1965, reanimated the approach of Poincaré.
The question about area-preserving transformations arises if you are thinking about mechanical systems with two degrees of freedom. If you have a mechanical system with more degrees of freedom, then the corresponding question is not about area-preserving transformations, but about transformations of higher-dimensional space that preserve what is called the symplectic form. Poincaré and Birkhoff understood this, but nobody explicitly formulated conjectures of that sort before Arnold.
In topology there is a theory of counting the number of fixed points of a map or diffeomorphism, which goes back to Brouwer and Lefschetz. But unlike the problem of Poincaré, all of this was governed by homology or related algebraic invariants of the manifold. Arnold realized, and actually proved in some very special situations, that in fact the bound on the number of fixed points is governed by Morse theory, so it is governed by the bound on the number of critical points of a function.
For instance, suppose you take a function on the annulus that is, say, constant on the boundary and grows if you go in. This function must have at least two critical points: the maximum and one other point. You can prove this in a standard way. Then — and actually Poincaré tried to do this in his paper — you can relate the question of fixed points of the transformation to a question about critical points of the function. But for a general transformation it was not clear how to do this.
Arnold started with one very specific conjecture about the 2-dimensional case, for area-preserving maps. Suppose you have an area-preserving transformation of the torus. Then you ask whether there are some fixed points. For the torus, an additional condition is needed, similar to the condition on the annulus that the map rotate the boundary circles in opposite directions; otherwise, you could just rotate the torus, and there would be no fixed points. A condition that Arnold called “preservation of center of mass” avoids such cases. Under this condition, Arnold said there must be three, and in the nondegenerate case four, fixed points. This was his first conjecture, just for the torus. Of course he understood that it’s not just about the torus and that you have a similar bound for surfaces. He made conjectures about manifolds of arbitrary dimension over the course of the next few years, up to the beginning of the 1970s.
I started to think about this, and Gromov also thought about it. It was clear that there is some phenomenon in two dimensions, because we already had the Poincaré theorem. So for surfaces, it was very likely that this would be true. At this time Gromov formulated what I call “the Gromov alternative,” which said that either essentially nothing in high dimension of this type is true, or everything is!
Suppose you have a diffeomorphism that preserves volume and that can be \( C^0 \) approximated by a diffeomorphism preserving the symplectic form. It is not clear whether the diffeomorphism itself has to preserve the symplectic form, because preservation of the symplectic form is a question about a derivative. If the approximation is only \( C^0 \) close, then a priori there is no reason to think that the limit will preserve this form. So Gromov said one of two things is true. Either it’s true that the limit has to preserve the symplectic form, or the completely opposite statement is true, that any volume-preserving diffeomorphism can be \( C^0 \) approximated by symplectic, so that if you manage to approximate by a symplectic diffeomorphism anything that is not symplectic, then essentially you can approximate whatever you want. If the latter were true, it would immediately follow that the Arnold Conjecture is wrong in dimensions bigger than 2.
So in some sense, it was not that we believed or did not believe, but there was this alternative. And there was absolutely no reason to think that A is true or B is true.
And they were starkly different.
Yes, but one of them would say that nothing like the Arnold Conjecture can be true in high dimensions, which would be an interesting result, but in some sense sad. That would show that the theory is not really interesting. There would be nothing there.
It’s extremely hard to solve equations of mechanics, but you would still like to be able to make some kind of qualitative statements, for instance, to say whether there are periodic orbits — to say something about the system, short of solving the equations of motion. Poincaré thought that merely the fact that the question is based on a mechanical system, together with some geometric constraints, means that some qualitative corollary should follow. And this is actually realized. All of the development of symplectic topology is the proof of this. The Gromov alternative was resolved in favor of rigidity.
A thriving field, but basic questions open

When you came to the US you were a little over 40 years old.
It was 1988, I had just turned 41.
Somehow I think of you as younger than your age, partly because you have a youthful way about you, but maybe also because the energy you brought to your work after coming to the US was that of someone younger.
The way I think about it is that at least eight years, the time when I was in Leningrad after I became a refusenik, should be subtracted from my mathematical life. So it should be counted that I left the USSR not at 41 but at 33! In some sense I started a completely new life. So indeed at 41, I was like a young postdoc in some sense.
Since that time symplectic and contact geometry has become a thriving field, and you are one of the central people in it. How do you see that development? Did it surprise you?
It didn’t surprise me. I knew it should happen. I remember giving lectures and trying to convince people that it’s something worth doing! But I was sure it would happen. Of course, I didn’t predict how it would develop, and now it has moved in different directions. With mirror symmetry and Kontsevich’s ideas, it moved toward algebraic stuff. There are many parts of this subject that I now don’t understand properly but still hope to understand.
Despite this area having fantastic success and many new results, some of the basic questions that I was thinking about 40 years ago are still not answered. So it’s only a partial success. Clearly we are waiting for a new door to open to go somewhere else.
Can you give an example of a basic result that is still open?
You can come to the symplectic world from different sides. You can come as a topologist, or you can come as a person from Hamiltonian dynamics and try to get some kind of dynamical consequences out of the symplectic topology. Both directions are completely valid, but let’s talk a little bit as a topologist.
As a topologist, you think of a symplectic structure as a geometric structure, and you would like to first understand which manifolds admit a symplectic structure — which manifolds are symplectic, which manifolds are contact, and so on.
A symplectic structure is a closed nondegenerate 2-form. If you remove the condition that the 2-form is closed, then you just have a nondegenerate 2-form, which is of course a necessary condition. A theorem of Gromov from a long time ago says that, for an open manifold, this condition is sufficient; the existence of symplectic structures is a purely homotopical condition. This is an instance of the h-principle, which is the idea that geometric problems should be solvable up to homotopy, once obvious topological obstructions vanish.
If you have a closed manifold, then you get one more necessary condition, that this symplectic form defines a 2-dimensional cohomology class of the manifold, which has the property that its powers have to be nonzero. So you get one more algebraic-topological constraint for the manifold to be symplectic.
The first naive question is, If a manifold satisfies this condition, does it admit a symplectic structure, or not? The answer is known only in dimension 4, and there the answer is no. A combination of the work of Gromov and Taubes implies this. But, if we go anywhere beyond 4 dimensions, the question is completely open. We have neither a construction of a counterexample, nor any tools to show that there is something else to obstruct the manifold to be symplectic in dimensions greater than 4. It’s completely open.
Nobody has any feeling about which way it might go?
Everybody has feelings, but these feelings are time-dependent and personal. I don’t have any idea. I would think that probably there is a soft answer, or that there are no other constraints. But I have no idea how this can be proven. All conjectures are extremely irresponsible because there is absolutely no reason to believe one way or the other.
There has been so much build-up of the subject, yet this basic question is still open.
Yes, that’s something. You can ask another question that is very similar. Suppose you take the space \( \mathbb{R}^{2n} \). In \( \mathbb{R}^{2n} \), there is a standard symplectic structure, a canonical, constant symplectic structure. Suppose you want to find a symplectic structure that outside some big ball is standard but inside the ball it is not. Can you find such a structure? Gromov proved that in dimension 4, this is impossible. All of them are standard. In dimension greater than 4, we have no idea.
Progress on both of these problems stops at dimension 4. What is different about dimension 4 that you can do something in that dimension?
In general, in dimension 4, topology is very different from other dimensions. In the symplectic world, the main reason comes from the following. Most of the rigidity results are proven using some version of Gromov’s theory of holomorphic curves on symplectic manifolds. Suppose in dimension 4 you have two surfaces that intersect transversally in finitely many points. The intersections can have plus or minus — each intersection has a sign depending on the orientation. For holomorphic curves, the sign is always plus. On the other hand, the total number of intersection points counting with signs is a topological invariant. Therefore, sometimes in dimension 4 you can guarantee that the two surfaces have no intersection, just using some topology. Nothing like this exists in higher dimensions. This is basically the reason.
Out of the darkness, into the sun
You left the USSR in late 1987. Where did you go right after you left?
There was a standard route of emigration. You were supposed to come to Vienna, and they processed your documents. Then they sent you to Italy, and you stayed in some suburb of Rome, waiting for a US visa. In mid-February of 1988, we got permission to go to America.
When you arrived in the US, did you have a job right away at Stanford?
No, but I had an absolutely fantastic thing. After the Berkeley Congress, I was invited by Alan Weinstein for a year program in symplectic geometry at MSRI.40 I got the invitation in 1986, when I was still in Leningrad. At the time, I considered it as some kind of joke, because I wouldn’t dream that I could get permission to go. But then I emigrated, so having the invitation was great.
The MSRI program started only in September 1988. So Andrew Casson suggested to me to write an extra proposal on his NSF [National Science Foundation] grant. I did this and received the grant, which supported me for three months. It was not much, but it was essential. Then, from September, I was at MSRI.
I should say that I was not sure I would be capable of doing mathematics, to be reborn as a mathematician. In Syktyvkar, I was able to do mathematics, but then there were the years when I was a refusenik. That was an extremely hard period, when I had to work as a computer programmer. It was a job that really took my brain completely. I caught myself at night thinking about how I could send a file from one place to another — I was thinking about that instead of mathematics. And I was too tired to do anything else. I tried to do some mathematics, and I even proved something, but it was not serious. So those eight years were essentially lost for me for mathematics. Therefore, when I emigrated, I was prepared to not be able to reinstate myself as a mathematician. I thought, Okay, maybe I’ll just find a job, do something interesting as a programmer.
But then, amazingly — especially thanks to this grant of Andrew Casson — I did quite a lot of nice work during that first half-year when I came to the US. I went on a tour of lectures, to Princeton, Stony Brook, University of Pennsylvania, NYU, University of Utah, University of Maryland at College Park, Caltech, USC, Stanford, Berkeley. Unexpectedly, I got offers from most of these places and decided to go to Stanford.
That is amazing that you could restart your mathematics. Why was that? The environment in Berkeley? Or were you finally able just to sit and think?
Maybe being able to sit and think, that’s the main thing. I got time to do mathematics. But of course the environment was also important. I’ll give you an example.
I was sitting in an office in Berkeley that I shared with a mathematician visiting from Spain, Jesús Gonzalo. Jesús was also working on contact manifolds. He told me what he was trying to prove, and I saw that it was completely impossible. That in some sense triggered me to think back about contact geometry. So indeed the environment was important also.

That was over the summer of 1988. Then I started the program at MSRI, and this was an absolutely fantastic time. I met and talked to so many people. That of course was extremely inspiring. I had met Claude Viterbo in Italy, but it was at MSRI that I first met Dusa McDuff, Helmut Hofer, and Floer. I met S.-S. Chern, Alan Weinstein, Rob Kirby, John Milnor. Also Curt McMullen was there — he was a postdoc, and I interacted with him. I also collaborated with Tudor Ratiu.
While I was in Italy right after leaving the Soviet Union I got in touch with many Italian mathematicians. Stefano Marchiafava was especially helpful. He organized my first series of lectures and paid me for that 360,000 Italian lire, which was about US\$300. I was extremely impressed by this huge amount and by the apparent lack of any bureaucracy. With my current experience, I strongly suspect that Stefano paid me out of his own pocket. After I gave these talks, they invited me for many others. I was touring Italy giving talks. I got an invitation to a conference in Cala Ganone, in Sardinia, which was in September 1988. I gave some lectures there and also stayed in Rome for some time, maybe for two weeks. And I remember one of my best works, which I like very much, is precisely what I thought about while walking in Rome!41
When I first came to the US, I came to Palo Alto because my brother and my mother were there. It was mid-February, it was fantastically sunny, there were no clouds, nothing. In the Soviet Union and Leningrad, it was pretty dark. I almost physically had this feeling that all my previous life was under dark clouds, and suddenly I had the sun.