Celebratio Mathematica

In the pre­face of his Dis­quisi­tiones Arith­met­icae, Gauss pro­claimed (or in­sisted) that di­o­phant­ine ques­tions do not con­sti­tute all of num­ber the­ory [e10]. A sim­il­ar dis­tinc­tion seems ap­pro­pri­ate when one con­tem­plates the con­tent and leg­acy of Mazur’s Ei­s­en­stein ideal pa­per. Ac­cord­ingly, the re­cur­ring and fecund theme of con­gru­ences between Ei­s­en­stein series and oth­er mod­u­lar forms will be con­sidered first in the con­text of the tor­sion the­or­em, and then for oth­er arith­met­ic­al, non­di­o­phant­ine pur­poses.

As Schap­pach­er and Schoof real­ized around 1994 [e46], Mazur’s tor­sion the­or­em had been for­mu­lated as a con­jec­ture in 1908 by Levi [e4] in his ad­dress to the in­ter­na­tion­al con­gress of math­em­aticians, and seem­ingly for­got­ten in the course of the 20th cen­tury. It is dif­fi­cult to trace ex­haust­ively the his­tory of this ques­tion. Levi had already noted that it amounts to prove that cer­tain curves (the nota­tion \( X_1(N) \) was an ana­chron­ism in 1908) do not have ra­tion­al points be­sides the ob­vi­ous ones (cuspid­al, in the mod­ern jar­gon). He es­tab­lished that no el­lipt­ic curve over \( {\mathbf Q} \) ad­mits a ra­tion­al point of or­der 14, 16 or 20 [e1], [e2], [e2], [e3]. His proof was based on the meth­od of des­cent, ap­plied to curves of genus no lar­ger than 1, the very tech­nique dat­ing back to Fer­mat and em­ployed by many con­tinu­at­ors of Levi, in­clud­ing, in a crown­ing achieve­ment, by Mazur. Con­sid­er­ing that the ques­tion was asked at the ICM, and that sig­ni­fic­ant par­tial res­ults were ob­tained, it is dif­fi­cult to fault Levi for hav­ing failed to dur­ably bring his con­jec­ture to the at­ten­tion of his con­tem­por­ar­ies and suc­cessors, and there­fore to deny him the pri­or­ity for his pre­dic­tion. Levi’s work pre­ceded Mor­dell’s proof of the fi­nite gen­er­a­tion of (what we call nowadays) the Mor­dell–Weil group, pub­lished in 1922 [e5].

Billing and Mahler [e6] (in 1940), with an ul­teri­or con­tri­bu­tion of Na­gell [e9] (in 1952) proved, still by study­ing curves of genus 1, that no el­lipt­ic curve over \( {\mathbf Q} \) pos­sesses a point of or­der 11, 15 or 24. Levi seems to have been for­got­ten by 1949, at least by Na­gell, who re­af­firmed the tor­sion con­jec­ture [e8] without ap­par­ent aware­ness of Levi’s work. In [e16], Ogg ruled out 17 as a pos­sible tor­sion prime. He pro­posed a geo­met­ric philo­sophy: \( X_1(N) \) should have non­cuspid­al \( {\mathbf Q} \)-ra­tion­al points if and only if the genus of \( X_1(N) \) is 0 (i.e., \( N\leq 10 \) or \( N=12 \)) [e21]. This was known to be equi­val­ent to the tor­sion con­jec­ture. Thus the once for­got­ten tor­sion con­jec­ture of Levi has some­times been re­ferred to as Ogg’s con­jec­ture.

All this was part of a wider back­ground of res­ults and con­jec­tures of which here is a sample. In 1967, Cas­sels at­trib­uted to the folk­lore the be­lief that the or­der of tor­sion of an el­lipt­ic curve over a num­ber field \( K \) is bounded in terms of \( K \) only [e11]. Sha­far­ev­ich had asked some­time be­fore 1972 wheth­er the bound in Cas­sels’ folk­lore con­jec­ture would de­pend only on the de­gree of \( K \) over \( {\mathbf Q} \) [e18]. Man­in proved in 1967 that, for any prime num­ber \( p \) and any num­ber field \( K \), the \( p \)-primary tor­sion of an el­lipt­ic curve over \( K \) is bounded in terms of \( p \) and \( K \) only [e13]. Both Dem’jan­en­ko and Hel­leg­ou­arch had noted an in­triguing con­nec­tion between hy­po­thet­ic­al solu­tions of Fer­mat’s equa­tion for the prime ex­po­nent \( p \) and the \( p \)-tor­sion of what would later be called the Frey el­lipt­ic curve [e14], [e15]. Serre had proved his open im­age the­or­em in 1972 [e19], set­ting forth the fol­low­ing state­ment:

Let \( E \) be an el­lipt­ic curve over a num­ber field \( K \) without com­plex mul­ti­plic­a­tions over \( {\bar K} \). For \( l \) prime num­ber, de­note by \( E_{l} \) the group of \( l \)-di­vi­sion points of \( E \). There ex­ists a num­ber \( N \) such that the rep­res­ent­a­tion \( \operatorname{Gal}({\bar{\mathbf Q}}/{\mathbf Q})\rightarrow \operatorname{Aut}(E_l) \) is sur­ject­ive for \( l > N \).

Serre asked about a uni­form ver­sion [e19]:

[…] peut-on pren­dre pour \( N \) un en­ti­er qui ne dépen­de que de \( K \) et pas de \( E \)?

Here is the ar­gu­ment that Mazur and Tate em­ployed to show that \( X_1(13) \) has no \( {\mathbf Q} \)-ra­tion­al points be­sides its cusps [1]. By “pure thought”, the au­thors meant that, con­tra their pre­de­cessors, they had no use of any mod­el for such a mod­u­lar curve. They pro­ceeded by em­bed­ding the curve \( X_1(13) \) in its jac­obi­an \( J_1(13) \), and then study­ing the \( {\mathbf Q} \)-ra­tion­al points of \( J_1(13) \).

Such an ap­proach had been fa­mil­i­ar for a long time. In par­tic­u­lar, Chabauty proved that, provided the rank \( r \) of Mor­dell–Weil group of the jac­obi­an \( J \) of a curve \( X \) over \( {\mathbf Q} \) is strictly smal­ler than the genus \( g \) of \( X \), then \( X({\mathbf Q}) \) is fi­nite [e7]. The con­di­tion \( r < g \) is Chabauty’s con­di­tion, a fun­da­ment­al guid­ing prin­ciple to this day. But es­tab­lish­ing fi­nite­ness dif­fers sig­ni­fic­antly from provid­ing the full list of ra­tion­al points. Falt­ings’ the­or­em [e27], proved in 1983 and fam­ously in­ef­fect­ive, would have been of no help to Mazur and Tate. In the set­ting of mod­u­lar curves, the lat­ter au­thors and Ogg com­bined an un­der­stand­ing of the arith­met­ic of \( J \) with some know­ledge of the geo­metry of the map \( X\rightarrow J \). Their suc­cessors would fol­low vari­ations of this ba­sic plan (see Pro­gram B be­low).

The key arith­met­ic ar­gu­ment is that the group \( J_1(13)({\mathbf Q}) \) is cyc­lic of or­der 19 and a for­tiori fi­nite. The proof is sum­mar­ized with ad­mir­able con­cision in the third para­graph of [1]:

The pos­sib­il­ity that this could be done oc­curred to us when Ogg passed through our town and men­tioned that he had dis­covered a point of or­der 19 on the 2-di­men­sion­al abeli­an vari­ety \( J \). It seemed (to us and to Swin­ner­ton-Dyer) that if such an abeli­an vari­ety \( J \), which has bad re­duc­tion at only one prime, and has a size­able num­ber of en­do­morph­isms, has a point of or­der 19, it is not en­titled to have any oth­er points.

Des­cent has been used by sev­er­al pre­de­cessors of Mazur and Tate in­clud­ing Levi, but ac­com­mod­at­ing the “siz­able num­ber of en­do­morph­isms” (i.e., the des­cent a with coef­fi­cients in a Hecke al­gebra) was a key in­nov­a­tion.

Thus the \( {\mathbf Q} \)-ra­tion­al points of \( X_1(13) \) are to be found among the 19 \( {\mathbf Q} \)-ra­tion­al points of \( J_1(13) \). It was known that only six of those points come from \( X_1(13) \), and they all come from the cusps.

From then on, the tor­sion con­jec­ture could be thought of as a di­o­phant­ine prob­lem devoid of di­o­phant­ine equa­tions.

We fol­low throughout Mazur’s un­usu­al choice of nota­tion: let \( N \) be a prime num­ber. The es­sen­tial step to prove the tor­sion con­jec­ture con­sists in prov­ing that \( X_1(N) \) has no ra­tion­al points, be­sides its cusps, for \( N=11 \) or \( N > 13 \) (call this the prime tor­sion con­jec­ture). The ad­di­tion­al ar­gu­ments needed to ob­tain the full tor­sion con­jec­ture have already been men­tioned or reside in two art­icles of Ligoz­at [e20] and Kubert [e23].

But the Mazur–Tate ar­gu­ment can not work for every value of \( N \) since \( J_1(N)({\mathbf Q}) \) was sus­pec­ted (and Mazur con­firmed this sus­pi­cion in [4], The­or­em 3) to be in­fin­ite ex­cept for fi­nitely many val­ues of \( N \). The modi­fic­a­tion in­tro­duced by Mazur con­sists in identi­fy­ing a nonzero quo­tient abeli­an vari­ety \( \tilde J \) of \( J_1(N) \) such that \( \tilde J({\mathbf Q}) \) is fi­nite or, more pre­cisely, \( \tilde J \) is the largest quo­tient of \( J_0(N) \) for which the meth­od of des­cent can be used to es­tab­lish the fi­nite­ness of \( \tilde J({\mathbf Q}) \).

For this, Mazur noted that the ring of en­do­morph­isms (over \( {\mathbf Q} \)) of \( J_0(N) \) iden­ti­fies to the (com­mut­at­ive) Hecke al­gebra \( {\mathbf T} \) (the sub­ring of the en­do­morph­isms of \( J_0(N) \) gen­er­ated by Hecke op­er­at­ors \( T_l \) for \( l \) prime num­ber \( l\ne N \), and by the Atkin–Lehner op­er­at­or \( W_N \)). The Ei­s­en­stein ideal \( {\mathcal I} \) of \( \mathbf{T} \) is gen­er­ated by the op­er­at­ors that would an­ni­hil­ate the single Ei­s­en­stein series of weight 2 for \( \Gamma_0(N) \). In prac­tice, it is spanned by the op­er­at­ors \( T_l-(l+1) \) for \( l \) prime num­ber \( l\ne N \), and by \( 1+W_N \). Mazur es­tab­lished two ba­sic prop­er­ties: the quo­tient ring \( {\mathbf T}/{\mathcal I} \) is iso­morph­ic to \( {\mathbf Z}/n{\mathbf Z} \), where \( n \) is the nu­mer­at­or of \( (N-1)/12 \), re­flect­ing the fact that \( (N-1)/24 \) is the con­stant coef­fi­cient (es­sen­tially a Bernoulli num­ber) of the Ei­s­en­stein series of weight 2 for \( {\Gamma}_0(N) \). The second prop­erty lies deep­er: \( {\mathcal I}/{\mathcal I}^2 \) is also a cyc­lic group of or­der \( n \), but it iden­ti­fies to the group \( (\mathbf{Z}/N{\mathbf Z})^\times/\mu_{12} \) where \( \mu_{12} \) is the group of 12th roots of unity. The lat­ter iden­ti­fic­a­tion is ob­tained by \( T_l-(l+1)\mapsto \text{class of } l^{(l-1)/2} \).

De­note by \( {\mathbf T}_{\mathcal I} \) the \( \mathcal I \)-ad­ic com­ple­tion of \( {\mathbf T} \). Then \( \tilde J \) is the largest quo­tient of \( J_0(N) \) on which \( {\mathbf T} \) acts through \( {\mathbf T}\rightarrow{\mathbf T}_{\mathcal I} \). Hence, \( \tilde J \) is called the Ei­s­en­stein quo­tient of \( J_0(N) \). The abeli­an vari­ety \( \tilde J \) is trivi­al if and only if \( n=1 \), i.e., \( N \) is equal to 2, 3, 5, 7 or 13.

For \( \mathcal M \) max­im­al ideal in the sup­port of \( \mathcal I \), Mazur con­siders the \( \mathcal M \)-ad­ic com­ple­tion of \( {\mathbf T} \) and defines the \( \mathcal M \)-Ei­s­en­stein quo­tient \( {\tilde J}_{\mathcal M} \) of \( {\tilde J} \). The des­cent of Mazur–Tate can be ad­ap­ted, del­ic­ately in terms of flat co­homo­logy, to show the fi­nite­ness of \( {\tilde J}_{\mathcal M}({\mathbf Q}) \), and de­duce the fi­nite­ness of \( \tilde J(\mathbf{Q}) \). But Mazur is more pre­cise: \( \tilde J({\mathbf Q}) \) is cyc­lic of or­der \( n \), and even iso­morph­ic to \( {\mathbf T}/{\mathcal I} \) as a \( \mathbf{T} \)-mod­ule. The des­cent provides in ad­di­tion a proof of the tri­vi­al­ity of the odd, \( \mathcal I \)-primary part of the Tate–Sha­far­ev­ich group of \( {\tilde J} \).

This en­ables one to prove two prop­er­ties of the whole of \( J_0(N) \) con­jec­tured by Ogg. First, the tor­sion part of \( J_0(N)({\mathbf Q}) \) iden­ti­fies to the cuspid­al sub­group (and to \( \tilde J({\mathbf Q}) \)). The oth­er prop­erty is of a dual nature: the max­im­al sub­group of \( J_0(N) \) of \( \mu \)-type (Carti­er dual of a con­stant group-scheme) is the Shimura sub­group, defined as the ker­nel of the morph­ism \( J_0(N)\rightarrow J_1(N) \) de­duced from \( X_1(N)\rightarrow X_0(N) \) by Pi­card func­tori­al­ity.

The con­sid­er­a­tion of the fi­nite­ness of \( \tilde J({\mathbf Q}) \) com­bined with the morph­ism \( \phi : X_1(N)\rightarrow J_1(N)\rightarrow \tilde J \) dir­ectly im­plies the fi­nite­ness of \( X_{1}(N)({\mathbf Q}) \) whenev­er \( \tilde J \) is nonzero. An ad­di­tion­al ana­lys­is of the geo­metry of \( \phi \) is re­quired to ob­tain the prime tor­sion con­jec­ture. The reas­on­ing of [4] will not be ex­plained here. In­deed, to ob­tain this de­sired con­clu­sion, Mazur provided a sim­pler and stronger ar­gu­ment in the iso­geny pa­per [5].

The iso­geny the­or­em, ob­tained by Mazur in 1978 in [5], is a sub­stan­tial gen­er­al­iz­a­tion of the tor­sion the­or­em.

At the time of [5], it was not known wheth­er the fol­low­ing num­bers should be al­lowed: 39, 65, 91, 125, and 169. This is­sue was cla­ri­fied by Ken­ku and Mestre [e24], [e25] soon af­ter­wards, and might ex­plain the pres­ence of the re­strict­ive qual­i­fi­er prime in the title of [5].

It is un­clear to me how pre­cisely this state­ment had been ex­pec­ted among spe­cial­ists. The fi­nite­ness of the list is not men­tioned as a folk­lore con­jec­ture in [e11]. It is asked by Serre (see above) [e19], who pro­posed a bound for non-CM curves. But Serre missed the ex­cep­tion­al prime num­ber \( N=37 \), which de­serves a men­tion. In­deed, Mazur and Swin­ner­ton-Dyer dis­covered in 1974 that \( X_0(37) \), of genus 2, ad­mits a pair of non-CM, non­cuspid­al, ra­tion­al points [2]. Ra­tion­al points of mod­u­lar curves are of­ten ex­plained by “geo­met­ric reas­ons” (the rel­ev­ant mod­u­lar curve has genus 0, or genus 1, the point cor­res­ponds to a CM-el­lipt­ic curve or a cusp). An am­bi­tious pro­ject would seek to ex­plain thus all al­geb­ra­ic points on mod­u­lar curves, though the no­tion of geo­met­ric reas­on needs to be cla­ri­fied. The find­ing of Mazur and Swin­ner­ton-Dyer for \( N=37 \) is the first sig­ni­fic­ant hurdle in such a pro­ject. Since then, oth­er not­able exot­ic al­geb­ra­ic points have been dis­covered, e.g., a quad­rat­ic point on \( X_0(311) \) by Gal­braith [e52] and a cu­bic point on \( X_1(21) \) by Na­j­man [e63].

The proof of the iso­geny the­or­em, and there­fore of the tor­sion the­or­em, is based on a single res­ult from [4]: the fi­nite­ness of \( \tilde J ({\mathbf Q}) \). Pres­ci­ently, Mazur found it use­ful to spell out in ax­io­mat­ic form what is needed: when \( N \) is equal to 11 or great­er than 13, there ex­ists a non­trivi­al quo­tient abeli­an vari­ety \( A \) of \( J_0(N) \) such that \( A({\mathbf Q}) \) is fi­nite. Such a cri­terion amends Chabauty’s con­di­tion: the rank of \( A \) is smal­ler than the di­men­sion of \( A \) (\( r < d \)). It is harm­less to sup­pose \( A \) op­tim­al, i.e., the morph­ism \( J_{0}(N)\rightarrow A \) has con­nec­ted ker­nel. In ef­fect, Mazur just con­sidered \( A={\tilde J} \) (see be­low for the pro­gress on Pro­gram B with a dif­fer­ent quo­tient \( A \)).

Mazur pro­ceeded as fol­lows. The es­sen­tial ques­tion is to de­term­ine for which prime num­bers \( N \) there ex­ists an el­lipt­ic curve over \( {\mathbf Q} \) ad­mit­ting a \( {\mathbf Q} \)-ra­tion­al sub­group \( C \) of or­der \( N \). Let \( E \) be such an el­lipt­ic curve. Mazur proved that \( j(E) \) is an in­teger away from 2. If not, an odd prime num­ber \( p \) would di­vide the de­nom­in­at­or of \( j(E) \). Then \( (E,C) \) defines a \( {\mathbf Q} \)-ra­tion­al point \( Q \) on \( X_0(N) \). Ex­tend \( X_0(N) \) to a mod­el \( {\mathcal X}_0(N) \) over \( \operatorname{Spec}{\mathbf Z} \), and the point \( Q \) to a sec­tion \( \hat Q \) : \( \operatorname{Spec}\, {\mathbf Z}\rightarrow {\mathcal X}_0(N) \). Since \( j(E) \) is not \( p \)-in­teg­ral, \( \hat Q \) co­in­cides with a cusp \( \hat Q_0 \) in the fiber at \( p \) of \( {\mathcal X}_0(N) \). Use \( \hat Q_0 \) as a base point to em­bed \( X_0(N) \) in \( J_0(N) \). Con­sider the morph­ism \( \phi \): \( X_0(N)\rightarrow J_0(N)\rightarrow A \). Then \( \phi(Q) \) is tor­sion since \( A({\mathbf Q}) \) is fi­nite. De­note by \( {\mathcal A} \) the Néron mod­el over \( \operatorname{Spec} {\mathbf Z} \) of \( A \). The morph­ism \( \phi \) ex­tends to the smooth locus \( {\mathcal X} \) of \( {\mathcal X}_0(N) \) as \( \hat{\phi} \): \( {\mathcal X}\rightarrow {\mathcal A} \). The sec­tion \( \hat Q \) be­longs to \( \mathcal X \). Fur­ther­more, the or­der of a \( \mathbf{Q} \)-ra­tion­al tor­sion point in an abeli­an vari­ety is de­term­ined in the spe­cial fiber at \( p \) (provided \( p > 2 \)). Thus one gets that \( \hat\phi(\hat Q)=\hat\phi(\hat Q_0) \) and \( \hat Q \) co­in­cides with \( \hat Q_0 \) in the fiber at \( p \) of \( A \). Mazur noted that this im­plies that \( \hat Q=\hat Q_0 \) (a con­tra­dic­tion) provided \( \hat\phi \) is a form­al im­mer­sion at the cusp \( \hat Q_0 \) in char­ac­ter­ist­ic \( p \). After a del­ic­ate re­in­ter­pret­a­tion in terms of mod­u­lar forms, this geo­met­ric con­di­tion turned out to be re­mark­ably simple: \( \hat\phi \) is a form­al im­mer­sion at the cusp \( \hat Q_0 \) in char­ac­ter­ist­ic \( p \), at least if \( p > 2 \), whenev­er \( A \) is non­trivi­al. Thus either \( \tilde J \) is trivi­al (and \( N=2 \), 3, 5, 7, or 13) or \( j(E) \) is in­teg­ral away from 2. (A vari­ant of this ar­gu­ment es­tab­lishes that \( N=2 \), 3, 5, 7, 13 or 17 or \( j(E) \) is fully in­teg­ral.)

One feels a kin­ship between Mazur’s form­al im­mer­sion ar­gu­ment and Chabauty’s meth­od, es­pe­cially Cole­man’s ex­pli­cit ver­sion via \( p \)-ad­ic in­teg­ra­tion [e29]. In­deed, Mazur’s ar­gu­ment has been trans­lated in­to Cole­man’s lan­guage by Baker [e50].

Mazur proved the iso­geny the­or­em for el­lipt­ic curves with non­in­teg­ral (away from 2) \( j \)-in­vari­ant by dif­fer­ent means, without any use of \( J_0(N) \). But the prime tor­sion the­or­em is easy in that case: Hasse’s the­or­em im­plies that an el­lipt­ic curve with a tor­sion point of or­der \( N \) with po­ten­tially good re­duc­tion at \( p \) sat­is­fies \( N < (1+p^{1/2})^2 \), which im­plies \( N < 8 \) for \( p=3 \). To ob­tain the iso­geny the­or­em, purely loc­al ar­gu­ments such as those do not suf­fice to sup­ple­ment the in­teg­ral­ity state­ment for \( j(E) \). But they con­strain \( N \) so much that either \( N=13 \) or \( {\mathbf Q}(\sqrt{-N}) \) has class num­ber 1 or \( N=37 \). The Hee­gn­er–Baker–Stark the­or­em im­poses that \( N\le 163 \) [e17], [e12].

The proof of Fer­mat’s Last The­or­em, by Wiles and Taylor–Wiles [e42], [e43], re­lied cru­cially on the tor­sion the­or­em. In­deed, a hy­po­thet­ic­al solu­tion to Fer­mat’s the­or­em, say \( a^N+b^N=c^N \), gives rise to the Frey–Hel­leg­ou­arch el­lipt­ic curve giv­en by \( y^2=x(x-a^N)(x+b^N) \), which in turn pro­duces a new­form of weight 2, level 2, mod­ulo \( N \). Such a form is a cusp form, and there­fore does not ex­ist, provided the rep­res­ent­a­tion of the ab­so­lute Galois group on the \( N \)-di­vi­sion point on the Frey–Hel­leg­ou­arch curve is ir­re­du­cible, i.e., the curve does not ad­mit a ra­tion­al iso­geny of de­gree \( N \). Be­cause of the semista­bil­ity of the curve, the full strength of Mazur’s iso­geny the­or­em is not re­quired, but there is no known sub­sti­tute to the tor­sion the­or­em to rule out the re­du­cib­il­ity.

In [5], Mazur asked wheth­er there ex­ist two el­lipt­ic curves \( E \), \( E^{\prime} \) over \( {\mathbf Q} \), non iso­gen­ous over \( {\mathbf Q} \), and a prime num­ber \( N\ge 7 \) such that \( E[N] \) and \( E^{\prime}[N] \) are iso­morph­ic as Galois mod­ules. The ques­tion was giv­en a pos­it­ive an­swer by Kraus and Oes­terlé [e38]. It de­veloped in­to what is com­monly called the Frey–Mazur con­jec­ture: Fix \( E \), does there ex­ist \( N_{E} \) such that the an­swer neg­at­ive for \( N\ge N_{E} \)? Here is a more am­bi­tious re­quest: Does there ex­ist \( N_{0} \) such that the an­swer is al­ways neg­at­ive for \( N\ge N_{0} \)? See [e32] for the con­sid­er­able con­sequences for vari­ants of Fer­mat’s Last The­or­em, and bey­ond.

The ques­tion seems as open in 2023 as it was in 1996. Pro­gram B pre­cedes Ques­tion C in [3], was re­peated ver­batim in open­ing sen­tence of [4] and res­on­ates with Serre’s uni­form­ity ques­tion (see above [e19]).

In­nu­mer­able works on the tor­sion points of el­lipt­ic curves, and their Galois-the­or­et­ic prop­er­ties have ap­peared in the 20th and 21st cen­tur­ies. Most of them have been writ­ten after the Ei­s­en­stein ideal pa­per. Many have ex­amined spe­cif­ic mod­u­lar curves over spe­cif­ic num­ber fields, have in­volved in­geni­ous ideas and com­puter cal­cu­la­tions. Dur­ing the week Septem­ber 18 to Septem­ber 22 2023, two sim­ul­tan­eous con­fer­ences, one in Zagreb, one in Ban­galore, were de­voted mostly to this top­ic, and chiefly to Mazur’s Pro­gram B [3].

The pro­gress be­longs to two gen­er­al dir­ec­tions which were already re­cog­nized around 1970: \( {\mathbf Q} \)-ra­tion­al points of oth­er mod­u­lar curves and al­geb­ra­ic points of \( X_{1}(N) \).

For \( K={\mathbf Q} \), a pos­it­ive an­swer to Serre’s prob­lem amounts to show that three fam­il­ies of mod­u­lar curves have no non-CM, non­cuspid­al \( {\mathbf Q} \)-ra­tion­al points when their prime level is large enough. The three fam­il­ies are \( X_0(N) \), \( X_{\mathrm{split}}^+(N) \) and \( X_{\mathrm{nonsplit}}^+(N) \). The curve \( X_0(N) \) have been treated by Mazur in [5]. After ad­di­tion­al work of Mo­mose [e28], Par­ent [e56], and Re­bolledo [e57], a break­through happened in 2008 when Bilu and Par­ent proved that the curve \( X_{\mathrm{split}}^+(N) \) has no non-CM, non cuspid­al ra­tion­al point for \( N \) large enough [e60] (it was es­tab­lished later for all \( N > 13 \) with the help of Re­bolledo [e61]). These au­thors fol­lowed Mazur’s meth­od to treat el­lipt­ic curves with non in­teg­ral \( j \)-in­vari­ant. They in­tro­duced two new ar­gu­ments to study el­lipt­ic curves with in­teg­ral \( j \)-in­vari­ant. Their first ar­gu­ment was bor­rowed from tran­scend­ent­al num­ber the­ory, in par­tic­u­lar the suc­cess­ive re­fine­ments of the iso­geny the­or­ems of Mass­er–Wüstholz [e34]. Those re­fine­ment, due to Dav­id [e44], Pel­lar­in [e53], and Gaud­ron–Rémond [e62], provided a lower bound (in term of \( N \)) for the log­ar­ithm of the \( j \)-in­vari­ant. The oth­er ori­gin­al ar­gu­ment of Bilu and Par­ent is an ad­apt­a­tion of Runge’s meth­od for in­teg­ral points on curves. It provides an up­per bound (in term of \( N \)) for the log­ar­ithm of the \( j \)-in­vari­ant, which con­tra­dicts the lower bound ob­tained by tran­scend­ence meth­ods when \( N \) is large enough.

Thus, the non-CM, non­cuspid­al ra­tion­al points of \( X_{\mathrm{split}}^+(N) \) for all prime num­bers \( N \) could be de­term­ined, ex­cept for \( N=13 \). This par­tic­u­lar level es­caped Mazur’s ap­proach, as the jac­obi­an of \( X_{\mathrm{split}}^+(13) \) does not pos­sess a nonzero quo­tient with fi­nitely many ra­tion­al points. The ab­sence of any non­trivi­al rank 0 quo­tient is the key as­pect of the jac­obi­ans of \( X_{\mathrm{nonsplit}}^+(N) \) which pre­vents the study the ra­tion­al points of \( X_{\mathrm{nonsplit}}^+(N) \) by Mazur’s meth­od. In­deed, even the amended ver­sion of Chabauty’s con­di­tion fails, as no quo­tient of the jac­obi­an sat­is­fies \( r < d \). Des­pite this in­aus­pi­cious situ­ation, the in­ex­ist­ence of non-CM, non­cuspid­al ra­tion­al points on \( X_{\mathrm{split}}^+(13) \) and \( X_{\mathrm{nonsplit}}^+(13) \) has been es­tab­lished by way of in­volved and prom­ising tech­niques, ad­ap­ted from Kim’s gen­er­al­iz­a­tion of Chabauty’s meth­ods, es­pe­cially when \( r=g \), by Bal­akrish­nan, Dogra, Müller, Tu­it­man and Vonk [e64]. One would hope that his­tory re­peats it­self, and that the break­through at level 13 would be fol­lowed by a gen­er­al res­ult. However, con­tra Mazur and Tate for \( X_{1}(13) \), [e64] re­lies on hand­ling spe­cif­ic mod­els of those mod­u­lar curves of genus 3. Fur­ther ef­forts along those gen­er­al lines [e69] so far do not provide yet com­plete lists of points on \( X_{\mathrm{nonsplit}}^+(N) \), which is the main prob­lem left for \( K=\mathbf{Q} \).

Sup­pose now that \( K \) is any num­ber field. Cas­sels’ “folk­lore con­jec­ture”, of­ten called the uni­form bounded­ness con­jec­ture, amounts to the in­ex­ist­ence of non­cuspid­al \( K \)-ra­tion­al point on \( X_1(N) \) when \( N \) is large enough (de­pend­ing on \( K \) only). The strength­en­ing sug­ges­ted by Sha­far­ev­ich, ac­cord­ingly called the strong uni­form bounded­ness con­jec­ture, would make the ‘large enough” de­pend on \( d=[K:{\mathbf Q}] \), as­sert­ing thus the nonex­ist­ence of non­cuspid­al \( {\mathbf Q} \)-ra­tion­al points on the \( d \)-th sym­met­ric power \( X_1(N)^{(d)} \) of \( X_1(N) \) for \( N \) large enough.

Kami­enny ex­ten­ded Mazur’s ap­proach ex­plained above in the fol­low­ing man­ner. Con­sider the map \( \phi_d \): \( X_0(N)^{(d)}\rightarrow A \) ob­tained by com­pos­ing the ca­non­ic­al maps \( X_0(N)^{(d)}\rightarrow J_0(N) \) and \( J_0(N)\rightarrow A \). It can be ex­ten­ded to a morph­ism \( \hat{\phi}_{d} \): \( {\mathcal X}^{(d)}\rightarrow {\mathcal A} \). Mazur’s ar­gu­ment in the iso­geny the­or­em ap­plies without much modi­fic­a­tion provided \( \hat{\phi}_d \) is a form­al im­mer­sion in some char­ac­ter­ist­ic \( p \), for \( p \) prime \( p > 2 \). Gen­er­al­iz­ing Mazur’s cri­terion for \( d=1 \), Kami­enny showed that the lat­ter con­di­tion is sat­is­fied when the first \( d \) Hecke op­er­at­ors are \( {\mathbf F}_p \)-lin­early in­de­pend­ent as en­do­morph­isms of \( \tilde A \). When \( A=\tilde J \), this means lin­ear in­de­pend­ence in \( {\mathbf T}/(p{\mathbf T}+I) \), where \( I \) is the ker­nel of \( {\mathbf T}\rightarrow{\mathbf T}_{\mathcal I} \) [e39]. Kami­enny proved this to be sat­is­fied when \( d=2 \) and \( N > 71 \) [e40] and then, with Mazur, when \( 2 < d\le 8 \), for \( N \) large enough [9]. Ab­ramovich in­tro­duced a vari­ant of this ar­gu­ment and showed that, when \( d\le 14 \), \( X_1(N)^{(d)} \) has non­cuspid­al ra­tion­al points for only fi­nitely many val­ues of \( N \) [e41]. As for an ana­logue of the tor­sion the­or­em for quad­rat­ic fields, Kami­enny de­term­ined a com­plete list of the prime num­bers that could di­vide the or­der of tor­sion sub­groups of el­lipt­ic curves over quad­rat­ic fields. The list of pos­sible tor­sion sub­groups for quad­rat­ic fields could be ob­tained with the help of Ken­ku and Mo­mose [e31].

All this was still based on \( A=\tilde J \) and the fi­nite­ness of \( {\tilde J}({\mathbf Q}) \). One hardly ima­gines how Mazur could have de­vised the wind­ing ho­mo­morph­ism in [4] without be­ing aware that the fi­nite­ness of \( {\tilde J}({\mathbf Q}) \) fol­lows from the Birch and Swin­ner­ton-Dyer con­jec­ture. However, the lat­ter con­jec­ture was terra in­cog­nita in 1977.

Con­sider the max­im­al quo­tient \( J_e \) (the wind­ing quo­tient, fol­low­ing the term in­tro­duced by Mazur and Swin­ner­ton-Dyer) of \( J_0(N) \) whose \( L \)-func­tion does not van­ish at 1. By 1994, it fol­lowed from the work of Gross–Za­gi­er [e30] and Kolyva­gin [e33] com­ple­men­ted by im­port­ant non­van­ish­ing res­ults due to Bump–Fried­berg–Hoff­stein [e36] and Murty–Murty [e37] that \( J_e({\mathbf Q}) \) is fi­nite. In \( J_{e} \), a more gen­er­al re­place­ment for the Ei­s­en­stein quo­tient has emerged [e45]. The ap­proach of Kami­enny–Mazur ap­plies with \( \tilde J \) re­placed by \( J_{e} \) and, mu­tatis mutandis, giv­en any \( d \), the re­quired lin­ear in­de­pend­ence has been es­tab­lished for \( N \) large enough, prov­ing thus the strong uni­form bounded­ness con­jec­ture [e45]. The meth­od has been im­proved by Oes­terlé and Par­ent [e51] and oth­ers to pro­gress with­in Pro­gram B. For ex­ample, De­r­ickx, Et­ro­pol­ski, van Hoeij, Mor­row and Zureick-Brown [e70] lis­ted com­pletely the pos­sible tor­sion sub­groups of el­lipt­ic curves over cu­bic fields.

Des­pite oc­ca­sion­al ul­teri­or oc­cur­rences [e68], the Ei­s­en­stein quo­tient ceased thus to be an in­dis­pens­able tool for fur­ther study of di­o­phant­ine ques­tions.

Gauss’ pro­nounce­ment that not all num­ber the­ory is di­o­phant­ine finds an echo in the fact that the Ei­s­en­stein ideal is, more than ever, an in­valu­able concept for al­geb­ra­ic num­ber the­ory. One might see in Ramanu­jan’s fam­ous con­gru­ence between \( \Delta \) and \( E_{12} \) mod­ulo 691, which pred­ates by far Mazur’s work, an early mani­fest­a­tion of this no­tion. It is bey­ond the scope of this ac­count to re­view all sub­sequent de­vel­op­ments (e.g., the proofs of the con­verse Herbrand the­or­em by Ribet [e22] and of Iwas­awa’s main con­jec­ture by Mazur and Wiles [7]).

Mazur in­tro­duced vividly the Ei­s­en­stein quo­tient by a scheme-the­or­et­ic pic­ture [4]:

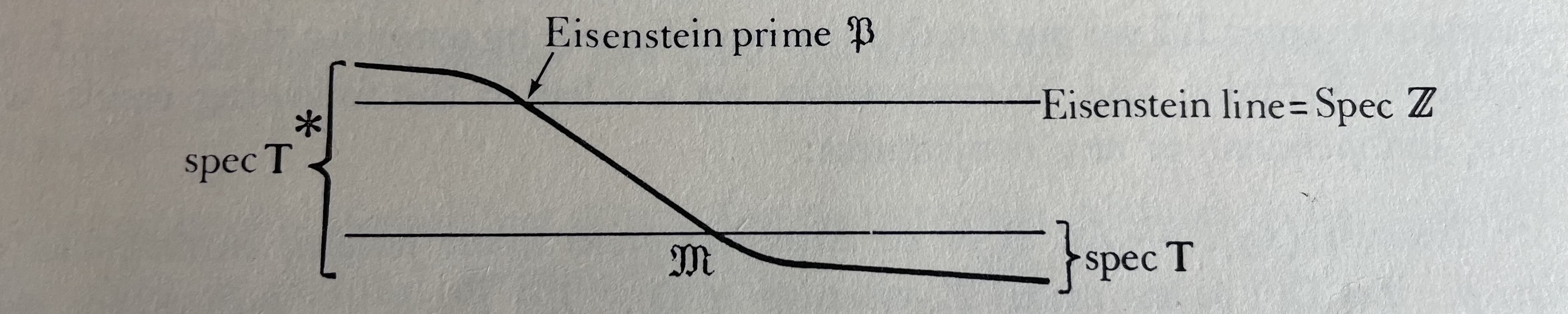
He seems to be first to have ex­amined \( {\mathbf T} \), or rather \( \operatorname{Spec}{\mathbf T} \), with the eye of a geo­met­er. The geo­met­ric view of the Hecke al­gebra fore­shad­owed the ei­gen­curve in­tro­duced in 1996 by Cole­man and Mazur [10]. Already in [4], Mazur found it worth­while to prove that \( \operatorname{Spec}{\mathbf T} \) is con­nec­ted, even if it is use­less for the tor­sion the­or­em.

To ac­com­plish the Ei­s­en­stein des­cent, it was im­port­ant to es­tab­lish that the com­ple­tion of \( {\mathbf T} \) at a max­im­al ideal \( {\mathcal M} \) is a Goren­stein ring, whenev­er \( \mathcal M \) is either of odd re­sid­ual char­ac­ter­ist­ic or Ei­s­en­stein. (In­stances of fail­ure of the Goren­stein prop­erty were found by Kil­ford in char­ac­ter­ist­ic 2 [e54], and the­or­et­ic­ally jus­ti­fied by Kil­ford and Wiese [e58].) This can be re­for­mu­lated as a “mul­ti­pli­city two the­or­em”: the \( {\mathcal M} \)-ad­ic Tate mod­ule of \( J_{0}(N) \) is free of rank 2 over \( {\mathbf T}_{\mathcal M} \). Sub­sequently, the Goren­stein prop­erty was proved for oth­er Hecke al­geb­ras [8], with the pur­pose of un­der­stand­ing Serre’s con­jec­ture. It played an im­port­ant part to prove many mod­u­lar­ity the­or­ems [e35], [e42], [e43], [e48]. An ad­dendum by Mazur to the ori­gin­al proof can be found in [e49].

Where­as new­forms and Galois rep­res­ent­a­tions used to be thought with coef­fi­cients in (com­pleted) al­geb­ra­ic num­ber fields, or their rings of in­tegers, Mazur brought to the fore the use­ful­ness and the ne­ces­sity to al­low coef­fi­cients in Hecke rings, whose sub­tleties, con­sequently, need to be stud­ied.

In­deed, fur­ther down in the in­tro­duc­tion of [4], one finds this proph­et­ic gem:

One may think of the “geo­met­ric des­cent” ar­gu­ment […] as a tech­nique of passing from the know­ledge of the arith­met­ic of the Ei­s­en­stein line (i.e., of Ei­s­en­stein series, and of \( {\mathbf G}_{\mathrm{m}} \)) to the know­ledge of the arith­met­ic of ir­re­du­cible com­pon­ents meet­ing the Ei­s­en­stein line (i.e., of \( \tilde J \)) by a “des­cent” per­formed at a com­mon prime ideal. One might hope that for oth­er prime ideals com­mon to dis­tinct ir­re­du­cible com­pon­ents (primes of fu­sion) one might make ana­log­ous pas­sages […].

Un­der all ap­pear­ances, Mazur had here in mind the ques­tion of un­der­stand­ing Selmer groups. However the philo­sophy of propaga­tion along the con­nec­ted com­pon­ents of \( \operatorname{Spec}{\mathbf T} \) was destined to be­come a cent­ral idea for auto­morph­ic forms, in par­tic­u­lar for many mod­u­lar­ity the­or­ems ob­tained so far in the Lang­lands pro­gram.

Mazur gave an ap­plic­a­tion of the prin­ciple of propaga­tion in a sub­sequent work: If a new­form \( f \) cor­res­ponds to an ir­re­du­cible line that meets the Ei­s­en­stein line, the \( L \)-value of \( f \) at 1 is in agree­ment with the Birch and Swin­ner­ton-Dyer for­mula (and vari­ous twis­ted for­mu­las) for this mod­u­lar form at this Ei­s­en­stein prime [6]. This line of in­quiry was pur­sued fur­ther by Stevens [e26].

In a sim­il­ar vein, Cre­mona and Mazur have shown that fu­sion between two cusp forms (es­pe­cially of un­equal Mor­dell–Weil ranks) pro­duces cer­tain ele­ments in Tate–Sha­far­ev­ich groups, that they call vis­ible [12]. If one of the mod­u­lar forms is at­tached to an el­lipt­ic curve \( E \) over \( {\mathbf Q} \), an ex­am­in­a­tion of a large set of ex­amples in­dic­ates that the Tate–Sha­far­ev­ich group of \( E \) is sur­pris­ingly of­ten made of vis­ible ele­ments.

The Ei­s­en­stein ideal the­ory makes a cru­cial ap­pear­ance in the con­jec­tures of Har­ris and Ven­katesh con­cern­ing mod­u­lar forms of weight 1 [e65]. Let \( f \) be a new form of weight 1 for \( \Gamma_1(M) \), for \( M \) in­teger prime to \( N \). Har­ris and Ven­katesh con­sider the mod­u­lar form \[ F_N(z)=\operatorname{Tr}^{\Gamma_1(M)\cap\Gamma_0(N)}_{\Gamma_0(N)}(f(z)f(Nz)), \] which is a cusp form of weight 2 for \( \Gamma_0(N) \). The mono­dromy of the Shimura cov­er­ing \( X_1(N)\rightarrow X_0(N) \) ap­plied to \( F_N \) pro­duces an ele­ment of \( ({\mathbf Z}/N{\mathbf Z})^{\times}/\mu_{12} \) (which iden­ti­fies to the Galois group of the max­im­al un­rami­fied cov­er­ing in­ter­me­di­ate to the Shimura cov­er­ing). This ele­ment is a pseudoei­gen­value of what Ven­katesh calls the de­rived Hecke op­er­at­or at \( N \) ap­plied to \( f \), as one of the first in­ter­est­ing spe­cial cases of his gen­er­al the­ory. In con­crete terms, Har­ris and Ven­katesh pro­ject \( F_N \) on the Ei­s­en­stein ei­gen­space and the pseudoei­gen­value turns out to be the coef­fi­cient of pro­por­tion­al­ity of \( F_N \) with the Ei­s­en­stein series.

Des­pite all of Mazur’s ef­forts, the Ei­s­en­stein ideal still holds in­trins­ic mys­ter­ies. The ring \( {\mathbf T}_{\mathcal I} \) is iso­morph­ic to \( \prod_{p|n}{\mathbf T}_{\mathcal P} \), where \( {\mathcal P}=p{\mathbf T}+{\mathcal I} \) is the max­im­al ideal of re­sid­ual char­ac­ter­ist­ic \( p \) in the sup­port of the Ei­s­en­stein ideal. For \( p \) Ei­s­en­stein prime num­ber, Mazur asked about the value \( r_p \) of the rank of \( {\mathbf T}_{\mathcal P} \) over \( {\mathbf Z}_{p} \) (see [4], page 140; and also What is this ele­ment \( u \)?, page 103). The in­vest­ig­a­tion of this prob­lem has fol­lowed two dis­tinct lines of in­quiry, which led to an­swers of a dif­fer­ent nature that can fruit­fully be com­pared. This situ­ation re­calls the clas­sic­al du­al­ism between the “al­geb­ra­ic” and “ana­lyt­ic” sides for the spe­cial val­ues of \( L \)-func­tions.

As­sume that \( p \) is not one of the un­ruly primes 2 and 3. Whenev­er \( r_p \) has small value can be ex­pressed in terms of val­ues mod­ulo \( N \) of cer­tain ana­logues of the zeta func­tion and its de­riv­at­ives (hence “ana­lyt­ic”). In con­crete terms, \( r_p \) is \( > 1 \) if and only if \( \prod_{k=1}^{(N-1)/2}k^k \) is a \( p \)-th power mod­ulo \( N \) or, al­tern­ately, in terms of su­per­sin­gu­lar el­lipt­ic curves, if and only if the dis­crim­in­ant of the Hasse poly­no­mi­al in char­ac­ter­ist­ic \( N \) is a \( p \)-th power) [e47], [e67].

Le­cou­tur­i­er in­tro­duced a high­er Ei­s­en­stein the­ory to fur­ther study \( r_p \) and gave vari­ous ele­ment­ary cri­ter­ia for \( r_p > 2 \) [e67]. The most in­ter­est­ing de­vel­op­ment on the “ana­lyt­ic side” in­volved Shari­fi’s con­jec­tures, and their vari­ants. The lat­ter con­jec­tures re­late \( p \)-ad­ic mod­u­lar sym­bols to the second \( K \)-group of the cyc­lo­tom­ic ring \( {\mathbf Z}[\mu_N,1/Np] \) [e59]. Le­cou­tur­i­er and Wang de­duced an iso­morph­ism (ex­pli­citly ex­pressed in terms of Stein­berg sym­bols) between \( {\mathcal I}^2/{\mathcal I}^3\otimes \mathbf{Z}_p \) and \( JK_2({\mathbf Z}[\mu_N,1/Np])/J^2K_2({\mathbf Z}[\mu_N,1/Np])\otimes\mathbf{Z}_p \), where \( J \) is the aug­ment­a­tion ideal of \( {\mathbf Z}[\operatorname{Gal}({\mathbf Q}(\mu_N)/{\mathbf Q})] \), which acts on \( K_2({\mathbf Z}[\mu_N,1/Np]) \) [e71]. They de­rived con­di­tion­al cri­ter­ia for \( r_p > 3 \). It seems that Shari­fi and Ven­katesh have gone a long way to prove Shari­fi’s con­jec­ture. But no cri­terion for \( r_p > 4 \) has been giv­en on the ana­lyt­ic side so far.

On the “al­geb­ra­ic side”, Calegari and Emer­ton ad­op­ted a dif­fer­ent per­spect­ive [e55]. They defined and stud­ied a ring from the the­ory of de­form­a­tion of (two-di­men­sion­al, re­du­cible) Galois rep­res­ent­a­tions without in­vok­ing mod­u­lar forms. By way of an \( R=T \) the­or­em, they proved that the ring they have in­tro­duced is iso­morph­ic to \( {\mathbf T}_{\mathcal I} \). They re­covered dir­ectly the prop­er­ties es­tab­lished by Mazur: struc­ture of \( {\mathbf T}/{\mathcal I} \), of \( {\mathcal I}/{\mathcal I}^2 \). To il­lus­trate the rel­ev­ance to al­geb­ra­ic num­ber the­ory, Calegari and Emer­ton have shown that \( r_p > 1 \) if the \( p \)-rank of the class group of \( {\mathbf Q}(N^{1/p}) \) is \( > 1 \), which, in turn, could be com­pared to the ana­lyt­ic cri­terion above. Wake and Wang-Er­ick­son, with a dif­fer­ent ap­proach of de­form­a­tion the­ory, and a dif­fer­ent \( R=T \) the­or­em, pro­ceeded fur­ther, and ex­pressed \( r_p \) purely in terms of Galois co­homo­logy us­ing Mas­sey products [e66]. About the ana­logy between re­lat­ing the dual ap­proaches of \( r_p \) to a con­jec­ture about \( L \)-val­ues, they asked:

[Wake and Wang-Er­ick­son’s the­or­em relates \( r_p \)] to an “al­geb­ra­ic side” (van­ish­ing of Mas­sey products). It is nat­ur­al to ask wheth­er there is a cor­res­pond­ing ob­ject on the ana­lyt­ic side — is there a zeta ele­ment \( \tilde\zeta \) such that \( \operatorname{ord}(\tilde\zeta)=r_p \)?

Loïc Mer­el has been pro­fess­or at Uni­versité Par­is Cité and at­tached to the In­sti­tut de Mathématiques de Jussieu-Par­is Rive Gauche since 1997.