by Tibor Macko
Andrew Ranicki dedicated the largest part of his mathematical life to surgery theory, a branch of topology that deals with classification problems of manifolds inside a given homotopy type. The total surgery obstruction (TSO) can be seen as the culmination of his work in this area. It provides in some sense a definitive answer to the following existence question: Given a space \( X \), when is it homotopy equivalent to a closed \( n \)-dimensional topological manifold? There is a closely related uniqueness question of such a manifold, and the TSO provides an answer here as well.
We will now make an informal formulation of the main theorem about the TSO and then we discuss the context, some applications and some ideas that go into the proofs. The prime sources are the paper [1] from 1979, and also the book [4] from 1992, which provided a reformulation and various improvements of the original treatment.
Given a finite simplicial complex \( X \), and an integer \( n \in \mathbb{Z} \), Ranicki defined an abelian group \( \mathbb{S}_{n} (X) \), as a certain cobordism group of chain complexes parametrized over simplices of \( X \) and equipped with an \( (n{-}1) \)-dimensional quadratic structure satisfying various conditions described in more detail below. For \( X \) a finite simplicial complex, which satisfies a suitable form of \( n \)-dimensional Poincaré duality, he defined an element \[ s (X) \in \mathbb{S}_{n} (X), \] called the TSO, and proved that, if \( n \geq 5 \), then \( s (X) = 0 \) if and only if \( X \) is homotopy equivalent to a closed \( n \)-dimensional topological manifold. Moreover, for \( X \) a closed \( n \)-dimensional manifold, and a homotopy equivalence \( h : M \rightarrow X \) of such manifolds, he defined an element \[ s (h) \in \mathbb{S}_{n+1} (X), \] called the structure invariant of \( h \), and proved that, if \( n \geq 5 \), then \( s (h) = 0 \) if and only if \( h \) is homotopic to a homeomorphism.
It is important that the groups \( \mathbb{S}_n (X) \) and \( \mathbb{S}_{n+1} (X) \) above are in many cases calculable in a practical sense, as they are a part of the algebraic surgery exact sequence, which was invented by Ranicki together with the TSO. This sequence contains the so-called assembly map, which has been extensively studied and about which many results have been proven. This knowledge can then be used to obtain information about the TSO via the algebraic surgery exact sequence.
To illustrate this method, we recall an application to the Borel conjecture, which says that any homotopy equivalence between two closed aspherical manifolds is homotopic to a homeomorphism. Given a closed \( n \)-dimensional aspherical manifold \( X \) with \( \pi_1 (X) = G \), such that the so-called Farrell–Jones conjecture about the assembly maps in both \( K \)-theory and \( L \)-theory holds for \( G \), the theory around the TSO can be used to show that \( \mathbb{S}_{n+1} (X) = 0 \). Hence any homotopy equivalence \( h : M \rightarrow X \) from any closed \( n \)-dimensional manifold \( M \) has \( s(h)=0 \) and is therefore homotopic to a homeomorphism. So the Borel conjecture holds for \( X \simeq BG \) in this case. There is an existence version of this conjecture and the TSO can be used to say a great deal about it too, but the statement is a bit more technical, so we relegate that discussion for later.
Let us now put the TSO into broader historical context. In 1956 Milnor found the first example of an exotic sphere, a 7-dimensional manifold \( \Sigma^7 \) homotopy equivalent, but not diffeomorphic to the standard sphere \( S^7 \). This raised the question of classification of homotopy spheres, which means smooth manifolds homotopy equivalent to the standard sphere, up to diffeomorphism. Surgery theory was born in 1963, when Kervaire and Milnor provided such a classification in their paper [e3], in terms of homotopy theory and quadratic forms over \( \mathbb{Z} \). The process of surgery was used when attempting to modify cobordisms to \( h \)-cobordisms, a task which may be impossible due to surgery obstructions.
If one is interested in classification of topological manifolds, then the generalized Poincaré conjecture says that there is up to homeomorphism only one topological manifold homotopy equivalent to the standard sphere. This conjecture was famously settled by Smale [e1], [e2] for PL-manifolds in dimensions \( \geq 5 \) and later by Newman [e4] for topological manifolds, and even later by others in all dimensions. However, even before these results there were known pairs of manifolds that were homotopy equivalent, but not homeomorphic, for example, the lens spaces; see [e13]. So the quest for nontrivial classification results of topological manifolds up to homeomorphism was certainly also interesting.
This required further work. Wall developed surgery theory for nonsimply connected manifolds in [e9]. Kirby and Siebenmann extended surgery theory to topological manifolds in [e6]. More ideas led to constructing what is now known as the Browder–Novikov–Sullivan–Wall surgery exact sequence, stated below as \eqref{eqn:ses}, reducing the classification of manifolds homotopy equivalent to \( X \) to homotopy theory and quadratic forms over \( \mathbb{Z}[\pi_1 X] \). It has a version for both smooth and topological manifolds, but the results happen to be more calculable in the topological case. This is due to the work of Sullivan, who described the homotopy type of the crucial classifying space \( \mathrm{G}/\text{TOP} \); see [e7]. We will discuss this space in more detail below; now we want to point out that the work of Sullivan starts from the abovementioned Poincaré conjecture, which from the classification point of view says that “the base case” of \( S^n \) has no other topological manifold in its homotopy type, while in the smooth case we may have many homotopy spheres.
This historical discussion has focused on the uniqueness part of the classification question so far, but it is important to mention that the existence part also played a role. The spherical space form problem, concerning the question of which finite groups admit free actions on spheres, and another question of which finite \( H \)-spaces are homotopy equivalent to manifolds were considered in the 1960s. These questions motivated the development of the theory, which would explain when is a topological space homotopy equivalent to a closed manifold. Moreover, the existence and uniqueness questions are closely linked. For a homotopy equivalence \[ h : \partial M_0 \rightarrow \partial M_1 \] where \( M_0 \) and \( M_1 \) are compact \( (n{+}1) \)-dimensional manifolds with boundaries \( \partial M_0 \) and \( \partial M_1 \), one can consider the topological space \[ X := M_0 \cup_{h} M_1. \] If \( h \) is homotopic to a homeomorphism, say \( h^{\prime} \), then the space \( X \) is homotopy equivalent to a closed \( (n{+}1) \)-dimensional manifold, say \( M = M_0 \cup_{h^{\prime}} M_1 \). So if methods can be developed to address this existence question, one can say something about the uniqueness question too. This is in the spirit of the well-known slogan in topology that “uniqueness is the relative form of existence”, which turned out to be fulfilled in surgery theory.
At this point it is necessary to mention some technical issues. In the above formulation of the existence question there are some obvious conditions, which the space \( X \) has to fulfill. Namely, it must be homotopy equivalent to a finite CW-complex satisfying Poincaré duality. Such complexes were provided in the context of the spherical space form problem, the finite \( H \)-spaces question, and the complex above obtained by gluing along a homotopy equivalence obviously also satisfies these conditions. Therefore a good technical formulation of the existence question is: Given a finite CW-complex satisfying Poincaré duality, is there a manifold homotopy equivalent to it?
Topological surgery produces the standard answer in a two-stage obstruction process. As we have seen, the TSO produces a single obstruction, which can be of advantage. We also emphasize again that the abelian group \( \mathbb{S}_{n} (X) \) invented by Ranicki is calculable in a practical sense. Andrew used to joke that if we did not take this requirement into account, then there would a very easy way of solving the two-stage deficiency. Namely, we could simply take the group \( \mathbb{Z}/2 \) and say that \( s(X) = 0 \), if the answer is yes, and \( s(X) = 1 \), if not. Of course, the problem would be that we would not have any realistic way of determining which case happens for a given \( X \).
Let us now briefly recall the classical surgery approach to the existence question. Given a finite \( n \)-dimensional Poincaré complex \( X \), the classical surgery theory asks first whether there exists a degree one normal map \[ (f, \overline{f}) : M \rightarrow X, \] from some closed \( n \)-dimensional manifold \( M \) to \( X \). Intuitively, if we want a homotopy equivalence, then we should obviously have a degree one map, possibly equipped with some bundle data, and this is perhaps easier to find. The bundle data are a microbundle map from the stable normal microbundle \( \nu_M \) to some microbundle \( \xi \) over \( X \).1 This setup is so made, that the associated spherical fibration \( S(\xi) \) of \( \xi \) will always be fiber homotopy equivalent to the so-called Spivak normal fibration \( \nu_X \) of \( X \). The Spivak normal fibration (SNF) is for Poincaré complexes an analogue of the stable normal microbundle of a manifold, and it is a unique spherical fibration in a specific sense. If a degree one normal map exists, then this spherical fibration comes from a topological microbundle. Conversely, if it comes from a topological microbundle, then by the topological version of the Pontrjagin–Thom construction one can construct a degree one normal map.
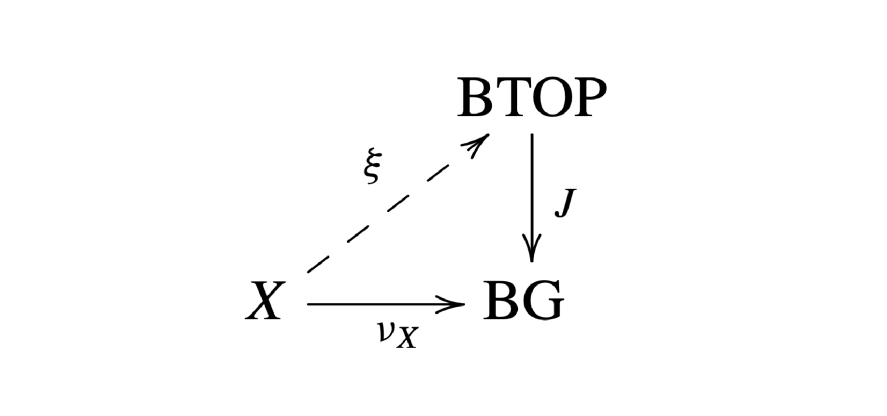
So the first obstruction is the obstruction to the existence of the topological microbundle reduction of the SNF, which can be formulated in terms of the classifying spaces of stable spherical fibrations \( \mathrm{BG} \), and of stable topological microbundles \( \mathrm{BTOP} \), and the canonical map \( J : \mathrm{BTOP} \rightarrow \mathrm{BG} \), as follows. It is the obstruction to the existence of a lift \( \xi \) of the classifying map \( \nu_X \) of the SNF of \( X \) in the diagram shown to the right.
If this first obstruction vanishes, i.e., if such a \( \xi \) exists, then the second obstruction is the surgery obstruction. Given a degree one normal map \( (f, \overline{f}) \), this is a well-defined element \[ \sigma_{n} (f, \overline{f}) \in L_{n} (\mathbb{Z} [\pi_{1} (X)]) \] in a certain abelian group \( L_{n} (\mathbb{Z} [\pi_{1} (X)]) \) defined using quadratic forms or formations, or chain complexes. The element itself is defined, when \( n = 2k \) and \( f \) is \( k \)-connected, by using the middle-dimensional intersection form on the kernel of the map induced by \( f \) and its quadratic refinement, which has to do with self-intersections of spheres representing elements in the kernel. In the odd-dimensional case the definition is more complicated, it involves the notion of a formation, which is an algebraic structure that can be obtained by studying automorphisms of quadratic forms, and we refrain from going into a more detailed discussion here.
The surgery obstruction has the property that \( \sigma_{n} (f, \overline{f}) =0 \) if and only if \( (f, \overline{f}) \) is normally cobordant to a homotopy equivalence, provided \( n \geq 5 \). Hence, if both obstructions vanish, then we obtain a positive answer to our question. However, observe that if the first obstruction vanishes, then we have to take into account all the possible lifts \( \xi \) of \( \nu_X \) and check the surgery obstruction of degree one normal maps associated to all of them to conclude a negative answer for a given \( X \). This may be quite hard to do in practice, which is the standard deficiency in a two-stage obstruction theory.
Both of the above obstructions can be located in the topological surgery exact sequence. It contains the structure set \( \mathcal{S}^{\text{TOP}} (X) \), which consists of homotopy equivalences \( f : M \rightarrow X \), where \( M \) is some \( n \)-dimensional closed manifold, up to homeomorphism in the source. The pairs \( (M,f) \) are called manifold structures on \( X \). It is clear that the classification questions we have been discussing so far can be formulated as follows:
- Existence question: Is \( \mathcal{S}^{\text{TOP}} (X) \) nonempty?
- Uniqueness question: If it is nonempty, what is it?
The next term appearing in the surgery exact sequence is that of the normal invariants \( \mathcal{N}^{\text{TOP}} (X) \), a cobordism group of degree one normal maps \( (f,\overline{f}) : M \rightarrow X \), as discussed above. The third term is the \( L \)-groups. Here it is also appropriate to mention that Ranicki clarified the existing theory of \( L \)-groups themselves by providing a definition as certain cobordism groups of finite chain complexes equipped with what he called a quadratic structure, which should be viewed as generalizing the notion of a quadratic form on a module to chain complexes. Among other advantages this gives a unified definition of \( L \)-groups independent of the parity of \( n \); see the foundational papers [2], [3].
Abbreviating \( \pi = \pi_1 (X) \), we can then give the topological surgery exact sequence as \begin{equation} \label{eqn:ses} \cdots \xrightarrow{\sigma_{n+1}\ } L_{n+1} (\mathbb{Z}[\pi]) \xrightarrow{\partial_{n+1}\ } \mathcal{S}^{\text{TOP}} (X) \xrightarrow{\eta_{n}\ } \mathcal{N}^{\text{TOP}} (X) \xrightarrow{\sigma_{n}\ } L_{n} (\mathbb{Z}[\pi]). \end{equation} The first obstruction in the above discussion vanishes if and only if the normal invariants \( \mathcal{N}^{\text{TOP}} (X) \) are nonempty; the second obstruction vanishes if and only if 0 is in the image of \( \sigma_{n} \).
This exact sequence is a great result that can be and was used in applications, but it also has conceptual problems. The \( L \)-groups are covariant, the normal invariants are contravariant, and the structure set has no obvious invariance at all. Moreover, there is a group structure on \( \mathcal{N}^{\text{TOP}} (X) \) given by the Whitney sum operation, but the map \( \sigma_n \) is not a homomorphism with respect to this structure, so it is only an exact sequence of pointed sets in a specific sense.
Fortunately, these problems can be overcome by the theory around Ranicki’s TSO. We first describe some ideas that lead to the reformulation of the part of the topological surgery that are related to the uniqueness question, and then return to the existence.
To prepare, note that Quinn [e5] has defined an \( \Omega \)-spectrum \( \mathcal{L}_{\bullet} \), such that \( \pi_{n} (\mathcal{L}_{\bullet}) = L_n (\mathbb{Z}) \), and it can be shown that the space \( \mathrm{G}/\text{TOP} \), defined as the homotopy fiber of the map \( J : \mathrm{BTOP} \rightarrow \mathrm{BG} \), is the 0th space \( \mathrm{G}/\text{TOP} \simeq \mathcal{L}_{0} \). Ranicki himself provided an algebraic version of these \( L \)-spectra \( \mathbf{L}_{\bullet} \langle 1 \rangle \) using his quadratic chain complexes theory and so one obtains \[ \mathcal{N}^{\text{TOP}} (X) \cong [X ; \mathrm{G}/\text{TOP}] \cong H^{0} (X;\mathcal{L}_{\bullet}) \cong H^{0} (X;\mathbf{L}_{\bullet} \langle 1 \rangle). \] Now, one may wonder whether there exists a kind of Poincaré duality with respect to the spectrum \( \mathbf{L}_{\bullet} \langle 1 \rangle \). Ranicki showed that for a Poincaré complex \( X \) with \( \mathcal{N}^{\text{TOP}} (X) \) nonempty, there are bijections \[ \mathcal{N}^{\text{TOP}} (X) \cong [X ; \mathrm{G}/\text{TOP}] \cong H^{0} (X;\mathbf{L}_{\bullet} \langle 1 \rangle) \cong H_{n} (X;\mathbf{L}_{\bullet} \langle 1 \rangle), \] making the normal invariants a covariant functor of \( X \).
Next he defined the so-called assembly maps \( \textup{asmb} : H_n (X;\mathbf{L}_{\bullet} \langle 1 \rangle) \rightarrow L_n (\mathbb{Z}[\pi]) \), so that the composition of the above Poincaré duality with this map produces the surgery obstruction map \( \sigma_n \). At this stage it was possible to make the first definition of \( \mathbb{S}_n (X) \) and the TSO in the paper [1].
However, Ranicki kept working on the topic and a much more developed version appears in his book [4]. A crucial ingredient is the chain complex version of the ordinary surgery which was already mentioned. Here the \( L \)-groups of a ring are cobordism groups of quadratic chain complexes and the surgery obstruction is defined at the chain complex level without the need for first making the degree one normal map highly connected. This leads to better functorial properties that are used later.
His next key idea is that he was able to define \( L \)-groups in the setting of additive categories with chain duality and later algebraic bordism categories. An example of an additive category with chain duality is the category of modules parametrized by simplices of a finite simplicial complex \( X \). A chain duality is a notion that allows one to consider a quadratic complex in such a category as a collection of quadratic complexes parametrized by the simplices with suitable compatibility condition. The algebraic bordism categories are a setup that enables defining various nondegeneracy conditions in this setting: one can ask for the complex to be Poincaré locally, meaning the complex over each simplex is Poincaré, or to be Poincaré globally, meaning the single complex obtained by assembling the complexes over all simplices is Poincaré. One can also specify a subclass of complexes that are to be considered, and an important class here is that of complexes that are locally Poincaré and globally contractible.
Given a degree one normal map \( (f,\overline{f}) : M \rightarrow X \) such that \( X \) is a triangulated manifold (this assumption may be weakened, but we do not want to go into such details here), one can make this map transverse to dual cells \( D(\sigma,X) \) and take the preimages to obtain for each simplex \( \sigma \in X \) a degree one normal map of manifolds with boundary \[ (f (\sigma), \overline{f} (\sigma)) : (M (\sigma) ,\partial M (\sigma)) \rightarrow (D(\sigma,X),\partial D(\sigma,X)). \] The collection of the quadratic chain complexes parametrized by the simplices \( \sigma \in X \) obtained from these degree one normal maps by taking the chain complex version of the surgery obstruction produces a quadratic complex which is locally Poincaré. Assembling the collection of these complexes to a single complex produces the chain complex version of the usual surgery obstruction. In case \( f \) is a homotopy equivalence one obtains a complex that is globally contractible, since its underlying chain complex is the homotopy fiber of the homotopy equivalence \( f \), which is contractible. However, such a complex may be locally not contractible — in fact we only know that it is locally Poincaré, since even if \( f \) is a homotopy equivalence, for a given \( \sigma \) the map \( (f (\sigma), \overline{f} (\sigma)) \) above may not be a homotopy equivalence.
These ideas can be put together in the algebraic surgery exact sequence and in the proof of its identification with the topological surgery exact sequence, which was already discussed. The terms in the algebraic surgery exact sequence are for a simplicial complex \( X \) with \( \pi_1 X = \pi \) and for any \( m \in \mathbb{Z} \) (sweeping some technical connectivity requirements under the rug):
| \( \mathbb{S}_{m} (X) \) | the \( L \)-group of locally Poincaré, globally contractible |
| \( (m{-}1) \)-dimensional quadratic complexes of \( X \); | |
| \( H_m (X;\mathbf{L}_\bullet \langle 1\rangle) \) | the \( L \)-group of locally Poincaré \( m \)-dimensional |
| quadratic complexes over \( X \); | |
| \( L_m (\mathbb{Z} [\pi]) \) | the \( L \)-group of globally Poincaré \( m \)-dimensional |
| quadratic complexes over \( X \). |
The above indicated construction of making a degree one normal map transverse to dual cells yields a map from the topological to the algebraic surgery exact sequence: \[ \minCDarrowwidth16pt \begin{CD} \cdots @>{{}}>{{}}> L_{n+1} (\mathbb{Z} [\pi]) @>{{}}>{{}}> \mathcal{S}^{\text{TOP}} (X) @>{{}}>{{}}> \mathcal{N}^{\text{TOP}} (X) @>{{}}>{{}}> L_n (\mathbb{Z} [\pi]) \\ @. @V{\cong}V{}V @V{\cong}V{s}V @V{\cong}V{t}V @V{\cong}V{}V \\ \cdots @>{{}}>{{}}> L_{n+1} (\mathbb{Z} [\pi]) @>{{}}>{{}}> \mathbb{S}_{n+1}(X) @>{{}}>{{}}> H_n (X,\mathbf{L}_\bullet \langle 1 \rangle) @>{{}}>{{\textup{asmb}}}> L_n (\mathbb{Z} [\pi]) @>{{}}>{{}}> \mathbb{S}_{n} (X) \end{CD} \] which is shown to be a bijection at all terms where it is defined.
Note that all the terms in the bottom row are \( L \)-groups of some algebraic bordism category and that the assembly map \( \textup{asmb} \) appears. This map happens to have a certain universal property, which characterizes it, and it also has many incarnations. In particular, there is a controlled topology version of it, which appears in the isomorphism conjectures of Farrell–Jones. These have been extensively studied and many results were achieved using it, such as the proof of the Borel conjecture for a vast class of groups, see for example [e12].
Finally, we come to the actual TSO and addressing the existence question in Ranicki’s setting. Note that in the above diagram both groups \( \mathbb{S}_{n+1} (X) \) and \( \mathbb{S}_{n} (X) \) appear. In fact the algebraic surgery exact sequence at the bottom is an exact sequence of abelian groups and can be extended infinitely also to the right. This is a major difference to the top sequence, which ends with \( L_n (\mathbb{Z} [\pi]) \). This is crucial from the point of view of the existence question since philosophically, if the uniqueness obstruction lives in \( \mathbb{S}_{n+1} (X) \), then the existence obstruction should live in its “delooping” \( \mathbb{S}_{n} (X) \) and this delooping is now existing. (In fact the bottom sequence is the long exact sequence of homotopy groups of a certain cofibration sequence of spectra.)
The TSO is an element in the group \( \mathbb{S}_{n} (X) \), which is a cobordism group of \( (n{-}1) \)-dimensional locally Poincaré, globally contractible quadratic complexes over \( X \). How can we obtain such an element out of an \( n \)-dimensional finite simplicial Poincaré complex \( X \)? The key property of such complexes \( X \) is that although they are Poincaré, they may not be locally Poincaré, meaning that for a given simplex \( \sigma \in X \) the dual cell \( (D(\sigma,X),\partial D(\sigma,X)) \) may not be a Poincaré pair. Observe that if \( X \) is a triangulated topological manifold, then these pairs are Poincaré, since they are in fact manifolds with boundary. Starting with an \( n \)-dimensional finite simplicial Poincaré complex \( X \), Ranicki first considers an \( n \)-dimensional globally Poincaré symmetric complex \( (C,\varphi) \) parametrized by simplices of \( \sigma \in X \), where the chain complex over each \( \sigma \) is \[ C (\sigma) := C (D(\sigma,X),\partial D(\sigma,X)), \] and there are certain compatibilities and certain duality maps (which are not chain equivalences in general) \begin{equation} \label{eqn:local-PD} C^{n-|\sigma|-\ast} (D(\sigma,X)) \rightarrow C (D(\sigma,X),\partial D(\sigma,X)), \end{equation} inherited from the global Poincaré duality \begin{equation} \label{eqn:global-PD} - \cap [X] : C^{n-\ast} (\widetilde X) \rightarrow C(\widetilde X), \end{equation} which is a \( \mathbb{Z}[\pi] \)-chain homotopy equivalence since \( X \) is Poincaré.
Ranicki next introduced the notion of algebraic boundary \( \partial
(E,\varphi) \) of an \( n \)-dimensional globally Poincaré symmetric
complex \( (E,\varphi) \) parametrized by simplices of \( X \), which is an
\( (n{-}1) \)-dimensional quadratic complex \( \partial (E,\varphi) = (\partial E,\partial
\varphi) \) again parametrized by simplices of \( X \), and which in some
sense measures the failure of the original complex to be locally
Poincaré. This \( (n{-}1) \)-dimensional quadratic complex always turns
out to be locally Poincaré and it is also globally contractible
since its underlying chain complex is the homotopy fiber of the global
Poincaré duality map \eqref{eqn:global-PD}, which is a chain
homotopy equivalence by assumption.
The TSO of \( X \), that means \( s (X) \in \mathbb{S}_{n} (X) \), is now defined by
taking first the \( n \)-dimensional globally Poincaré symmetric complex
\( (C,\varphi) \) parametrized by simplices of \( \sigma \in X \) described
above, and then taking its algebraic boundary \( \partial (C,\varphi) =
(\partial C,\partial \varphi) \), which is now an \( (n{-}1) \)-dimensional quadratic
complex again parametrized by simplices of \( X \), and which is locally
Poincaré and globally contractible and thus represents an element in
\( \mathbb{S}_{n} (X) \). The underlying chain complex \( \partial C (\sigma) \) over
each simplex \( \sigma \in X \) turns out to be the homotopy fiber of the
chain map from \eqref{eqn:local-PD}. Further technical details of the
construction are beyond the scope of this article, but we hope that
the above description of the underlying chain complex provides some
intuition.
In summary, we see that the TSO in some sense measures the failure of local Poincaré duality of a geometric Poincaré complex. The idea that failure of such a local Poincaré duality obstructs the positive answer to the existence question is quite natural. What was hard here was finding the setup (that means the right kind of \( L \)-groups), such that vanishing of the element obtained using this idea guarantees the existence of a manifold in the homotopy type of \( X \). The proof is very long, and it involves in particular also all of the classical surgery. We refer the reader to [1], [4], [e14].
We promised an application to the existence version of the Borel
conjecture. It is as follows. Given a torsionfree group \( G \), such that
\( BG \) is an \( n \)-dimensional finite simplicial complex, which satisfies
Poincaré duality, and the Farrell–Jones conjecture in \( K \)-theory and
\( L \)-theory holds for \( G \), then the theory around the TSO can be used
to identify the TSO with the so-called Quinn obstruction, which is
\( \mathbb{Z} \)-valued. If this obstruction vanishes, then we obtain that \( BG \)
is homotopy equivalent to a closed \( n \)-dimensional topological
manifold (see, for example,
[e10]).
Further applications can be found in part II of the book [4], including recovering the previously known examples of Poincaré complexes that are not homotopy equivalent to manifolds, such as the example of a 4-dimensional complex found in the 1960s by Wall in Example 22.28 of [4], and a discussion of other versions of the TSO, notably a version for ANR homology manifolds.
We would like to mention that the proof of the identification of the geometric and algebraic surgery exact sequence is done in parallel with the proof of the main theorem about the TSO. It has also the following corollary. The structure invariant provides us with a bijection \[ s : \mathcal{S}^{\text{TOP}} (X) \xrightarrow{\cong\ } \mathbb{S}_{n+1} (X), \] whose target is an abelian group. As a result we obtain an abelian group structure on \( \mathcal{S}^{\text{TOP}} (X) \) as well, but it is unclear what is its geometric interpretation. This remains an interesting open problem.
The theory and applications of TSO form an impressive collection of ideas that encompasses much of the area of classification of manifolds in topology. Many contributions of Andrew Ranicki starting from his thesis were in the spirit of trying to find conceptual treatments and algebraic explanations of various beautiful geometric phenomena that occur here. It often means that one needs to grasp a huge body of material, but one is rewarded by a deep understanding. The TSO is a prime example where all this was achieved.
Let us also not forget that the TSO is still a topic of contemporary research. For example, in 2011 Lurie posted online lecture notes [e11], where he offered his own perspective on algebraic surgery and the TSO by providing a treatment in the setup of \( \infty \)-categories. This was taken up recently by others and a spectacular collaboration appeared starting with [e15], where various aspects of algebraic surgery were applied to the study of the relationship between hermitian \( K \)-theory and \( L \)-theory. Although this work has not yet directly addressed the TSO, it is closely related and might bring new insights in the future.
Besides providing the topology community with the vast body of interesting mathematical literature Andrew Ranicki was a central figure in this area and had a very distinctive presence wherever he appeared. Much about his kind personality has been said at the online conference in his honor in 2021. Just like many other topologists the author of this note benefited greatly from the interactions with Andrew and from his generosity and hospitality. I especially recall the fall semester in 2008, when he gave a semester-long lecture course about algebraic surgery in Münster. Although I had known some of his theory before, it was great to build on that, and also to study it with a large group of people including his students. It was just one manifestation of his lasting positive influence on how the topology community functions.
Thank you everything, Andrew!
Tibor Macko is an Associate Professor at the Faculty of Mathematics, Physics and Informatics of the Comenius University and a Research Fellow at the Institute of Mathematics of the Slovak Academy of Sciences, both in Bratislava, Slovakia.