Celebratio Mathematica

A prin­cip­al goal of to­po­logy has al­ways been that of find­ing reas­on­able sets of ax­ioms for to­po­lo­gic­al char­ac­ter­iz­a­tions of stand­ard to­po­lo­gic­al spaces. Of course at­ten­tion was first fo­cused on the sim­pler spaces: the in­ter­val, the line, the circle. Once the ba­sic no­tions of sep­ar­a­tion and com­pact­ness were worked out, these prob­lems be­came quite tract­able. The circle, for ex­ample could be char­ac­ter­ized as a con­tinuum (com­pact and con­nec­ted met­ric space) which is non-de­gen­er­ate (that is, not a point) and is sep­ar­ated by each pair of points. Two di­men­sion­al spaces such as the 2-sphere presen­ted a much more chal­len­ging set of prob­lems. This was a prin­cip­al fo­cus of to­po­logy in the first third of this cen­tury. In­deed, R. L. Moore’s book can be in­ter­preted as a sweep­ing and his­tor­ic­al defin­i­tion of the plane, start­ing from first con­cepts.

By the mid-thirties, there were sev­er­al sat­is­fact­ory char­ac­ter­iz­a­tions of the 2-sphere, but the most el­eg­ant one, sug­ges­ted by J. R. Kline, re­mained un­solved: Sup­pose that a nonde­gen­er­ate Peano con­tinuum \( X \) is sep­ar­ated by each to­po­lo­gic­al 1-sphere in \( X \), but is sep­ar­ated by no to­po­lo­gic­al 0-sphere; is \( X \) a 2-sphere? It fol­lowed from work of Zip­pin, and van Kampen (see [1]) that the an­swer is af­firm­at­ive if no arc sep­ar­ates \( X \). Many to­po­lo­gists at­temp­ted to re­move this last con­di­tion. Bing suc­ceeded.

This res­ult, ob­tained shortly after his Ph.D., re­ceived much at­ten­tion. Bing was marked as a young math­em­atician of great prom­ise. That prom­ise was well kept.

The post­war peri­od in Po­land (1920s) was one of fab­ulous de­vel­op­ment in to­po­logy. A prin­cip­al in­terest was the study of plane con­tinua, both “well be­haved” (that is, loc­ally con­nec­ted) and patho­lo­gic­al. Some­what re­flect­ing the au­da­city of the time were the fol­low­ing two ques­tions:

1. If a non-de­gen­er­ate plane con­tinuum is homeo­morph­ic to each of its nonde­gen­er­ate sub­con­tinua, is it ne­ces­sar­ily an arc?
2. If a nonde­gen­er­ate plane con­tinuum is ho­mo­gen­eous, is it ne­ces­sar­ily a simple closed curve?

The first ques­tion was raised by Mas­urkiewicz in volume 2 of Fun­da­menta Math­em­at­ica, the oth­er was raised by Knas­ter and Kur­atowski in volume 1.

There can be little doubt that these ques­tions were re­garded as tough nuts, and that they were vig­or­ously at­tacked. The 288 pages of volume 2 of Fun­da­menta that sep­ar­ates these ques­tions con­tains five pa­pers by Kur­atowski, Knas­ter, and Mazurkiewicz on re­lated prob­lems. Volume 3 in­cludes a pa­per by Kur­atowski on ho­mo­gen­eity. The same volume has, in suc­cess­ive pa­pers by Knas­ter, two fam­ous ex­amples of exot­ic con­tinua.

These Knas­ter con­tinua have his­tor­ic­al im­port­ance. A con­tinuum is called “de­com­pos­able” if it is the uni­on of two prop­er sub­con­tinua. On first thought it would be reas­on­able to as­sume that every con­tinuum is de­com­pos­able, but the ex­ist­ence of in­decom­pos­able con­tinua was dis­covered by Brouwer in his dis­proof of the con­jec­ture of Schön­flies, that the com­mon bound­ary of two plane re­gions is de­com­pos­able. Knas­ter’s first ex­ample, now called the buck­et-handle or \( U \)-con­tinuum, is an el­eg­ant and prob­ably the simplest ex­ample of a plane in­decom­pos­able con­tinuum, that is, a con­tinuum in the Eu­c­lidean plane that is not the uni­on of two prop­er sub­con­tinua. The second ex­ample, con­struc­ted as the in­ter­sec­tion of a de­creas­ing se­quence of bands, each very crooked in­side its pre­de­cessor, has the fur­ther prop­erty that it is hered­it­ar­ily in­decom­pos­able, that is, each of its sub­con­tinua is in­decom­pos­able. It plays a spe­cial role in this talk, so I shall refer to it as the Knas­ter con­tinuum.

Volume 3 of Fun­da­menta con­tains a long pa­per by Kur­atowski on vari­ous prop­er­ties as­so­ci­ated with in­decom­pos­able con­tinua. There is every reas­on to be­lieve that Kur­atowski, Knas­ter, Mas­urkiewicz et al. had strong sus­pi­cions that, if the ques­tions (1) and/or (2) have neg­at­ive an­swers, then the counter­examples would be as exot­ic as Knas­ter’s but, as we shall see, the truth is more as­ton­ish­ing than they could have sus­pec­ted.

Prob­lem (1) proved to be quite in­tract­able, and per­haps began to be per­ceived as un­nat­ur­al, in the sense that neither a pos­it­ive nor neg­at­ive an­swer seemed likely to in­flu­ence fu­ture re­search. Some head­way was made, not­ably by Why­burn, but des­pite an at­tempt by Wilder in 1937 to pop­ular­ize the prob­lem, it was to re­main un­solved for an­oth­er ten years.

Prob­lem (2) at­trac­ted more at­ten­tion. The hy­po­thes­is of ho­mo­gen­eity seemed to of­fer more to work with, and the fact that the prob­lem could be re­cast in terms of a group ac­tion (the trans­it­iv­ity of the homeo­morph­ism group) made the prob­lem seem nat­ur­al (in the sense that a pos­it­ive or neg­at­ive an­swer might dir­ect fu­ture re­search). Al­though Mazurkiewicz proved in 1924 that the an­swer is af­firm­at­ive if the con­tinuum is loc­ally con­nec­ted, there was little fur­ther pro­gress. In fact, the situ­ation was ob­scured by an un­for­tu­nate suc­ces­sion of pa­pers con­tain­ing false res­ults in­volving sev­er­al au­thors.

In 1947, Moise in his Ph.D. dis­ser­ta­tion (Trans. A.M.S. 63 (1948), pp. 581–594) de­scribed a gen­er­al con­struc­tion which pro­duced a fam­ily of to­po­lo­gic­ally equi­val­ent plane con­tinua hav­ing the prop­erty that they were hered­it­ar­ily in­decom­pos­able and homeo­morph­ic to each of their nonde­gen­er­ate sub­con­tinua, thus neg­at­ively set­tling prob­lem (1). He noted that the Knas­ter con­tinuum (which, by the way, had been in Knas­ter’s dis­ser­ta­tion) was very sim­il­ar, if not in fact to­po­lo­gic­ally equi­val­ent, to Moise’s con­tinuum.

Moise’s meth­ods were of course more power­ful than Knas­ter’s. In­stead of Knas­ter’s bands, Moise used a se­quence of “chains” of open sets to define his “pseudo-arcs.” These chains were re­fined by chains whose pat­terns be­came suc­cess­ively more crooked with re­spect to the pre­ced­ing chains. This guar­an­teed that the con­tinuum would be hered­it­ar­ily in­decom­pos­able. By a pro­cess of “con­sol­id­a­tion” (the prin­ciple be­ing that a suf­fi­ciently crooked chain could be con­sol­id­ated in­to a chain of re­quired pat­tern, as needed), Moise showed that all con­tinua con­struc­ted in this way, that is, all pseudo-arcs, are homeo­morph­ic. He then showed that each nonde­gen­er­ate sub­con­tinuum of a pseudo-arc is a pseudo-arc, and hence homeo­morph­ic to it.

I must con­fess at this point that my un­der­stand­ing of Moise’s work is ret­ro­spect­ive, and in­flu­enced by Bing’s sub­sequent pa­pers. The full im­port of Moise’s con­struc­tion was ob­scured by sev­er­al factors. Moise’s chains did not cov­er the con­tinuum, their clos­ures did, but the links were pair­wise dis­joint. This com­plic­ated the con­struc­tions, and made their sym­metry less trans­par­ent. Fur­ther­more, the ex­pos­i­tion, while lack­ing no pre­ci­sion, was not a mod­el of clar­ity. The hy­po­thes­is of The­or­em Nine, for ex­ample, takes some 270 words.

Bing must have coped with these dif­fi­culties as he tried to fol­low Moise’s proof. My guess is that he tried to re­cast Moise’s ideas in­to more com­pre­hens­ible bits, and fit the ideas clearly in­to place. Bing [2] defined the pseudo-arc us­ing chains of open cov­ers and form­al­ized the no­tion of pat­tern. By an in­tric­ate and subtle use of con­sol­id­a­tions, he suc­ceeded in prov­ing that the pseudo-arc is ac­tu­ally ho­mo­gen­eous! (It should be men­tioned here that, hav­ing seen Bing’s pa­per, Moise showed that ho­mo­gen­eity could also be de­duced from his work.)

In a later pa­per, Bing [4] put the fi­nal piece of the puzzle in place. He showed that the pseudo-arc is the only hered­it­ar­ily in­decom­pos­able chain­able con­tinuum. This meant that Knas­ter’s con­tinuum is a pseudo-arc. In oth­er words, Knas­ter’s con­tinuum is a counter­example to both prob­lems (1) and (2). (It is an in­ter­est­ing co­in­cid­ence that, as par­tial re­quire­ments for their Ph.D., both Knas­ter and Moise sub­mit­ted the same ex­ample.)

The pseudo-arc is one of the most fant­ast­ic and unique con­struc­tions in to­po­logy. Like the Can­tor set, the pseudo-arc has a simple de­scrip­tion, a fractal con­struc­tion, is ho­mo­gen­eous, and is ubi­quit­ous. Like an arc, it doesn’t sep­ar­ate the plane, is homeo­morph­ic to each of its prop­er sub­con­tinua, and has the fixed point prop­erty. Like a simple closed curve, it is ho­mo­gen­eous and has ar­bit­rar­ily small open cov­ers of cir­cu­lar chains. It is ubi­quit­ous. (Bing showed [4] that, in the cat­egory sense, al­most all con­tinua are pseudo-arcs. Wayne Lewis re­cently proved that, in the cat­egory sense, al­most every map between con­tinua is an em­bed­ding of one pseudo-arc in­to an­oth­er.) A prin­cip­al theme of this con­fer­ence is the in­ter­ac­tion of con­tinua the­ory and dy­nam­ic­al sys­tems. The dis­crete dy­nam­ics of the pseudo-arc is likely to pro­duce some re­mark­able phe­nom­ena.

The ex­cit­ing de­vel­op­ments con­cern­ing the pseudo-arc nat­ur­ally fueled the search for oth­er ho­mo­gen­eous plane con­tinua. Were they now all known, the circle and the pseudo-arc? Bing [4] sug­ges­ted a cir­cu­lar ver­sion of the pseudo-arc, called the pseudo-circle, as a pos­sible ex­ample. At first blush, this con­tinuum would ap­pear a more likely can­did­ate than the pseudo-arc it­self, but Fearn­ley (Bull. A.M.S. 75 (1969), pp. 554–558) and Ro­gers (Trans. A.M.S. 148 (1970), pp. 417–428) in­de­pend­ently proved that it was not ho­mo­gen­eous. However, in 1954 Bing and Jones in­de­pend­ently con­struc­ted an­oth­er ho­mo­gen­eous con­tinuum, the “circle of pseudo-arcs” [11]. In the 33 years suc­ceed­ing the Bing–Jones ex­ample, much pro­gress has been made in the search for ho­mo­gen­eous plane con­tinua, not­ably by Jones and his school. Bing [11] re­turned to this prob­lem in 1960 and proved that the circle is the only ho­mo­gen­eous plane con­tinuum that con­tains an arc. The list of known ex­amples still stands at three, and the list of pos­sible types of ex­amples has been shortened, but the prob­lem re­mains un­solved.

R. L. Moore’s stu­dents were in­tro­duced to to­po­logy via “Moore spaces” rather than Haus­dorff spaces. In mod­ern ter­min­o­logy, a Moore space is a reg­u­lar Haus­dorff space with a se­quence \( G_1, G_2, \ldots \) of open cov­ers such that for each point \( x \) and neigh­bor­hood \( N(x) \) there is an \( n \) such that every ele­ment of \( G_n \) that con­tains \( x \) lies in \( N(x) \). It was a ques­tion of long stand­ing wheth­er a nor­mal Moore space is met­riz­able. Many of Moore’s stu­dents and grand-stu­dents (and Moore him­self) worked on this prob­lem. Bing, of course, also worked on this prob­lem, but did not solve it. This is for­giv­able (as it is in­deed for all of those who at­temp­ted it), as the prob­lem turned out to be un­de­cid­able. However, in work­ing on it, Bing [3] de­veloped a very in­ter­est­ing prop­erty which he called “col­lec­tion­wise nor­mal.” A Haus­dorff space is col­lec­tion­wise nor­mal if each dis­crete col­lec­tion of pair­wise dis­joint closed sets can be covered by pair­wise dis­joint open sets. He then proved that a col­lec­tion­wise nor­mal Moore space is met­riz­able, then gave a beau­ti­ful ex­ample of a nor­mal Haus­dorff space that is not col­lec­tion­wise nor­mal.

In the same pa­per (and in the same spir­it) was the fol­low­ing the­or­em, now known as the Bing Met­riz­a­tion The­or­em: A ne­ces­sary and suf­fi­cient con­di­tion that a reg­u­lar Haus­dorff space be met­riz­able is that it have a sigma-dis­crete basis, that is, a basis \( G = \bigcup G_n \) such that each \( G_n \) is dis­crete. In­de­pend­ently, Nagata and Smirnov de­rived sim­il­ar res­ults with “loc­ally fi­nite” re­pla­cing “dis­crete.”

A con­vex met­ric space is a met­ric space in which, for each two points \( a \) and \( b \), there is a third point \( c \) such that \( d(a,b) = d(a,c) + d(c,b) \). In 1928, Menger had proved that a com­pact con­vex met­ric space is a Peano con­tinuum, and asked wheth­er the con­verse were true: Does each Peano con­tinuum have a con­vex met­ric? This prob­lem re­ceived much at­ten­tion. There was a dis­cus­sion of it in Blu­menth­al’s book, Dis­tance geo­met­ries (1938), and par­tial res­ults were es­tab­lished by Kur­atowski, Why­burn, and Har­rold. In 1938 Beer pub­lished an af­firm­at­ive solu­tion for the one-di­men­sion­al case.

In 1948, Bing was at Madis­on, and Moise at Ann Ar­bor. Both were work­ing on the Menger prob­lem. Bing pub­lished an af­firm­at­ive solu­tion in 1949 for the fi­nite-di­men­sion­al case. Shortly af­ter­ward, Moise an­nounced a proof for the gen­er­al case, and a few weeks later Bing an­nounced his proof. Their pa­pers ap­peared back to back in the A.M.S. Bul­let­in. Un­for­tu­nately, Moise’s pa­per had a ser­i­ous er­ror. In­ter­est­ingly, both pa­pers em­ployed the no­tion of what Bing called “par­ti­tion­ing.” This no­tion of pair­wise-dis­joint open sets whose clos­ures cov­er the space is re­min­is­cent of Moise’s ap­proach to the pseudo-arc.

We now get to the area that was to dom­in­ate Bing’s in­terest for the rest of his ca­reer.

In a talk he gave in 1955, Bing ex­pressed his views on the dir­ec­tion he felt that geo­met­ric to­po­logy should take:

There has been much study de­voted to the plane, and simple prob­lems that have not already been at­tacked are dif­fi­cult to find in this area… On the oth­er hand, \( \mathbb E^3 \) is es­sen­tially a vir­gin forest. For many years the prob­lems were so for­bid­ding that few at­tacks were suc­cess­ful. Now math­em­aticians are be­gin­ning to ven­ture in­to the woods.

In 1949 Bing had vis­ited the Uni­versity of Vir­gin­ia and, ac­cord­ing to Bing, he be­came in­ter­ested in 3-space after con­ver­sa­tions with Ed Floyd. In the mean­time, Moise had turned his in­terest to \( \mathbb E^3 \) and had broken hard ground with his mo­nu­ment­al series of pa­pers, “Af­fine struc­tures on 3-man­i­folds” (An­nals of Math., 1951–1954). Moise had tri­an­gu­lated 3-man­i­folds (without bound­ary) and proved the Hauptver­mu­tung for 3-man­i­folds. Bing had pub­lished his pa­per on the sum of two horned spheres in 1952 (I will re­turn to this pa­per in a later sec­tion) and in 1954 Bing had pub­lished his first ma­jor pa­per on tri­an­gu­la­tion, “Loc­ally tame sets are tame” [5]. This pa­per ap­peared back to back in the An­nals of Math. with Moise’s “Af­fine struc­tures…” The con­tent of both these pa­pers is sim­il­ar, and both pa­pers leaned heav­ily on Moise’s earli­er work.

For sim­pli­city of ex­pos­i­tion I shall de­scribe the res­ults in \( \mathbb E^3 \), al­though the proofs work in an ar­bit­rary tri­an­gu­lated man­i­fold. A sub­set \( K \) of \( \mathbb E^3 \) is called tame if there is a homeo­morph­ism of \( \mathbb E^3 \) car­ry­ing \( K \) onto a poly­hed­ron. It is called loc­ally tame if, for each point \( p \) of \( K \), there is a neigh­bor­hood \( N(p) \) and a homeo­morph­ism of the clos­ure of \( N \) in­to \( \mathbb E^3 \) that car­ries both the clos­ure of \( N \) and its in­ter­sec­tion with \( K \) onto poly­hedra. The main the­or­em is the title of Bing’s pa­per. An­oth­er im­port­ant res­ult in their pa­pers is that each 3-man­i­fold with bound­ary can be tri­an­gu­lated, ex­tend­ing Moise’s work to man­i­folds with bound­ary. (This res­ult is needed, for ex­ample, to prove the an­nu­lus the­or­em in three di­men­sions, al­though the prob­lem was not ex­pli­citly for­mu­lated at the time.)

In 1955, at the time of the quo­ta­tion at the be­gin­ning of this sec­tion, Bing [7] had just proved his Ap­prox­im­a­tion The­or­em for Sur­faces: If \( M \) is a 2-man­i­fold with bound­ary in a tri­an­gu­lated 3-man­i­fold \( S \), and \( f \) is a non-neg­at­ive con­tinu­ous func­tion defined on \( M \), then there is a man­i­fold \( M^{\prime} \) and a homeo­morph­ism \( h \) of \( M \) onto \( M^{\prime} \) such that \( M^{\prime} \) is loc­ally poly­hed­ral at \( h(x) \) if \( f(x) > 0 \) and \( d(x,h(x))\leq f(x) \). This the­or­em will play a fun­da­ment­al role in Bing’s work. At a cru­cial place it uses Moore’s plane de­com­pos­i­tion the­or­em.

In 1959, Bing pub­lished his “Al­tern­at­ive proof that three-man­i­folds can be tri­an­gu­lated” [9]. A key in­gredi­ent of this pa­per is a strength­en­ing of the ap­prox­im­a­tion the­or­em for man­i­folds, to an ap­prox­im­a­tion the­or­em for 2-com­plexes; that is, the man­i­fold of the pre­vi­ous res­ult is re­placed by an ar­bit­rary to­po­lo­gic­ally em­bed­ded 2-com­plex. The pa­per is a com­pletely self-con­tained proof of both the tri­an­gu­la­tion the­or­em and Hauptver­mu­tung for 3-man­i­folds with or without bound­ary. It also es­tab­lishes that each homeo­morph­ism of a 3-man­i­fold can be ap­prox­im­ated by piece­wise-lin­ear ones (Moise had done this in the un­boun­ded case).

Roughly speak­ing, Bing’s early pa­pers in this area rely on Moise’s main res­ults from “Af­fine struc­tures, 1–5.” By 1954, they are work­ing in­de­pend­ently and get­ting sim­il­ar res­ults. After Bing’s “Al­tern­ate proof that three man­i­folds can be tri­an­gu­lated,” their work takes dif­fer­ent dir­ec­tions.

In 1958, Bing [8] pub­lished his “Ne­ces­sary and suf­fi­cient con­di­tions that a 3-man­i­fold be \( \mathbb S^3 \).” In or­der to put this pa­per in­to per­spect­ive, it will be ne­ces­sary and, I hope, suf­fi­cient to re­call The Fox–Artin arc (An­nals of Math. (1948), pp. 979-990) which has a simply con­nec­ted com­ple­ment in \( \mathbb S^3 \) even though its com­ple­ment is not \( \mathbb E^3 \) (see Fig­ure 1).

Fox and Artin showed that the simple closed curve \( W \) in the com­ple­ment of the arc is null-ho­mo­top­ic, but there is no homeo­morph­ism of the com­ple­ment of the arc that trans­forms \( W \) in­to the in­teri­or of a ball. “It seems to us that the ex­ist­ence or non-ex­ist­ence of a closed simply con­nec­ted three-di­men­sion­al man­i­fold with this prop­erty would be a de­cis­ive point in solv­ing the Poin­caré Con­jec­ture.” Bing’s the­or­em is that a closed 3-man­i­fold is \( \mathbb S^3 \) if each simple closed curve lies in a to­po­lo­gic­al 3-ball. It is a sharp the­or­em, of the form: \( (\pi_1(M) = 0) + \varepsilon \) im­plies \( M = S^3 \). Bing sug­ges­ted, and Mc­Mil­lan later proved, that an even sharp­er hy­po­thes­is suf­fices: every simple closed curve is null-ho­mo­top­ic with­in some sol­id tor­us.

In 1958, Bing [17] proved the power­ful Side Ap­prox­im­a­tion The­or­em: If a 2-sphere is in \( \mathbb E^3 \) and \( \varepsilon > 0 \), then there is an \( \varepsilon \)-homeo­morph­ism of the sphere in­to a poly­hed­ral one which is strictly on a giv­en side of the sphere, ex­cept pos­sibly for a fi­nite num­ber of \( \varepsilon \)-disks.

Bing used this res­ult to prove that

1. each disk in \( \mathbb E^3 \) con­tains a tame arc [16];
2. each disk in a \( \mathbb E^3 \) is pierced by a tame arc [15];
3. a sur­face (or a Can­tor set) is tame if its com­ple­ment is 1-ulc [14], [13].

The 1-ulc pa­per [14] can be called the real be­gin­ning of tam­ing the­ory. It is at the root of much of the de­vel­op­ment of high­er-di­men­sion­al to­po­logy.

An­oth­er fun­da­ment­al res­ult of Bing’s in tam­ing the­ory is the the­or­em that a 2-sphere in \( \mathbb E^3 \) is tame if it can be ap­prox­im­ated by spheres (not ne­ces­sar­ily tame) from either side. Let me leave this sub­ject by ob­serving that Bing and his stu­dents found a num­ber of re­mark­able ap­plic­a­tions of these ideas.

In the 1920s R. L. Moore proved the fol­low­ing: If \( G \) is an up­per semi­con­tinu­ous de­com­pos­i­tion of the plane in­to con­tinua, not one of which sep­ar­ates \( \mathbb E^2 \), then the de­com­pos­i­tion space is \( \mathbb E^2 \). (A par­ti­tion of a space in­to con­tinua is up­per semi­con­tinu­ous if each con­tinuum in the col­lec­tion is “at least as large” as nearby con­tinua; that is, if \( N(C) \) is a neigh­bor­hood of a con­tinuum in the par­ti­tion, then there is a smal­ler neigh­bor­hood \( V(C) \) such that each con­tinuum in the par­ti­tion in­ter­sect­ing \( V(C) \) lies in \( N(C) \). The de­com­pos­i­tion space is the quo­tient space ob­tained by identi­fy­ing each of the con­tinua to a point.) The proof was as fol­lows: Us­ing a to­po­lo­gic­al char­ac­ter­iz­a­tion of the plane, Moore proved that the de­com­pos­i­tion space sat­is­fies the same ax­ioms. This of course is an over­sim­pli­fic­a­tion! The proof has been de­scribed as a tour de force of 2-di­men­sion­al to­po­logy.

The cor­res­pond­ing prob­lems for \( \mathbb E^3 \) were at the heart of Bing’s math­em­at­ic­al in­terest throughout his ca­reer: What is a simple use­ful to­po­lo­gic­al char­ac­ter­iz­a­tion of \( \mathbb E^3 \), and which mono­tone de­com­pos­i­tions (that is, com­pact con­nec­ted de­com­pos­i­tion ele­ments) of \( \mathbb E^3 \) pro­duce a de­com­pos­i­tion space homeo­morph­ic to \( \mathbb E^3 \)?

Why­burn had ob­served that even with only one nonde­gen­er­ate de­com­pos­i­tion ele­ment, a simple arc, the de­com­pos­i­tion space might not be \( \mathbb E^3 \). (For ex­ample, if \( a \) is the Fox–Artin arc pre­vi­ously men­tioned, then \( \mathbb E^3/a \) is not \( \mathbb E^3 \), as \( \mathbb E^3 - a \) is not simply con­nec­ted.) Why­burn sug­ges­ted that, per­haps, one should there­fore study “point­like” de­com­pos­i­tions of \( \mathbb E^3 \), that is, those in which the com­ple­ment of each ele­ment is homeo­morph­ic to the com­ple­ment of a point. In fact, us­ing this ter­min­o­logy, Moore’s the­or­em be­comes: Each point­like (up­per semi­con­tinu­ous) de­com­pos­i­tion of \( \mathbb E^2 \) has \( \mathbb E^2 \) as its de­com­pos­i­tion space. As for to­po­lo­gic­al char­ac­ter­iz­a­tions of \( \mathbb E^3 \), Wilder had pos­tu­lated that the space should have the loc­al ho­mo­logy groups of 3-space (that is, a gen­er­al­ized man­i­fold), but no-one seemed to have even a good sug­ges­tion for a simple set of ax­ioms (nor is there one at this time!).

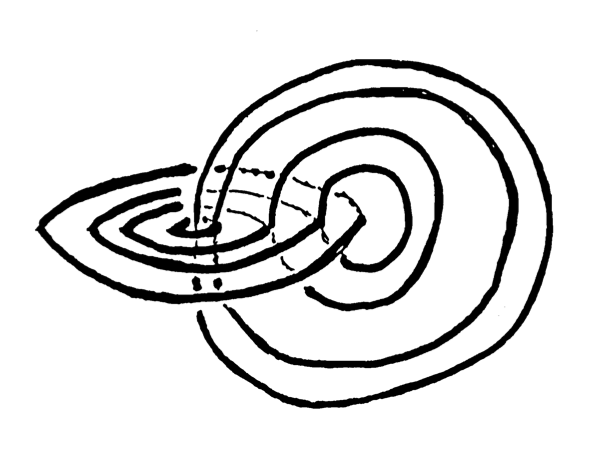
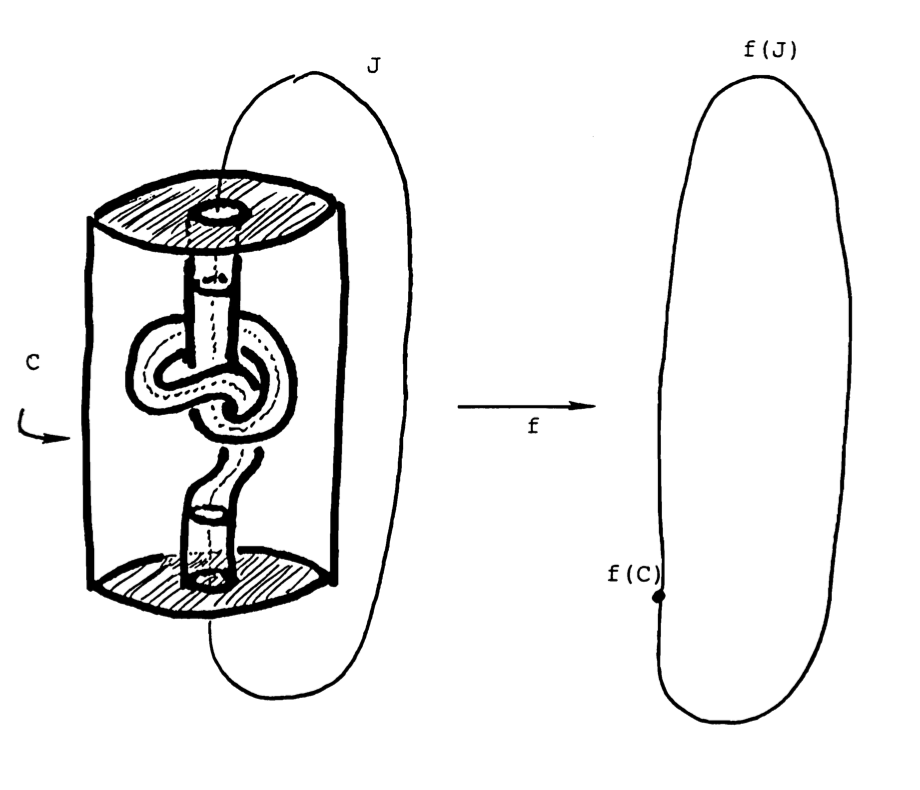
Fig­ures 2 and 3 il­lus­trate two subtle as­pects of de­com­pos­i­tion the­ory.

Fig­ure 2 il­lus­trates a strik­ing ex­ample (due to Bing \citeyear{36}) of a mono­tone de­com­pos­i­tion of \( \mathbb E^3 \) in­to points, circles, and fig­ure-eights. The de­com­pos­i­tion space is \( \mathbb E^3 \) even though the two circles link. Bing and Moise gave en­tirely dif­fer­ent proofs of this (In­sti­tute in Set The­or­et­ic To­po­logy, 1955) and each proof is a les­son in the sub­tlety of de­com­pos­i­tion the­ory.

In the second ex­ample, due to the au­thor, there is only one de­com­pos­i­tion ele­ment, and it is point­like, so the de­com­pos­i­tion space is \( \mathbb E^3 \). But the quo­tient map car­ries the knot­ted arc \( J \) homeo­morph­ic­ally onto an un­knot­ted arc. Bing was to dis­cov­er an even more subtle fact: it is pos­sible to “link” bunches of arcs to­geth­er even though each pair in the bunch is poly­hed­ral. But I am get­ting ahead of the nar­rat­ive.

Bing’s very first pa­per on \( \mathbb E^3 \) (1951) was an at­tempt to provide at least some set of ax­ioms. Un­for­tu­nately, the ax­ioms were not par­tic­u­larly use­ful or il­lu­min­at­ing. His second pa­per, however, was a block­buster. Bing showed that \( \mathbb S^3 \) is the uni­on of two sol­id horned spheres sewn to­geth­er along their bound­ary. First of all, the con­struc­tion provides an in­vol­u­tion of \( \mathbb S^3 \) whose fixed-point set is a horned sphere, that is, an in­vol­u­tion that could not be con­jug­ate to a lin­ear in­vol­u­tion. An im­port­ant con­sequence of this con­struc­tion was that the the­ory of trans­form­a­tion groups moved in the dir­ec­tion of dif­fer­en­tial to­po­logy in or­der to avoid patho­logy.

But it was Bing’s meth­od of proof that was both start­ling and sem­in­al. He used “de­com­pos­i­tion the­ory.” Bing con­struc­ted a cer­tain point­like de­com­pos­i­tion of \( \mathbb E^3 \) and showed that (1) the de­com­pos­i­tion space could be viewed as the uni­on of two horned spheres, and (2) the de­com­pos­i­tion space is homeo­morph­ic to \( \mathbb E^3 \). The meth­od that Bing used to prove (2) in­volved a pro­ced­ure whereby the de­com­pos­i­tion ele­ments were gradu­ally “shrunk” to smal­ler sets without al­low­ing the oth­er de­com­pos­i­tion ele­ments to grow too large. This tech­nique grew in­to what McAuley later named “Bing’s shrink­ing cri­terion.”

Let’s stop for a mo­ment and see what the situ­ation would have been if the de­com­pos­i­tion space were not \( \mathbb E^3 \). In that case Bing would have con­struc­ted a de­com­pos­i­tion of \( \mathbb E^3 \) in­to points and tame arcs whose de­com­pos­i­tion space is not \( \mathbb E^3 \), show­ing that Why­burn’s sug­ges­ted ver­sion for a Moore The­or­em in \( \mathbb E^3 \) would not work. Thus, Bing had a ma­jor res­ult whichever way it came out.

When it turned out that the de­com­pos­i­tion space was \( \mathbb E^3 \), Bing im­me­di­ately star­ted try­ing to frus­trate this out­come, that is, he tried to frus­trate the shrink­ing trick. The res­ult of his ef­forts was per­haps Bing’s greatest con­struc­tion, the dog­bone space [6]. The de­com­pos­i­tion ele­ments are still points and tame arcs, but they can­not be shrunk uni­formly small. Bing showed that if the de­com­pos­i­tion space were \( \mathbb E^3 \), then it would be pos­sible to shrink the ele­ments. (This was a neg­at­ive ap­plic­a­tion of the shrink­ing cri­terion.) In his ar­gu­ment, Bing used a del­ic­ate prop­erty of \( \mathbb E^3 \): a cer­tain pair of in­ter­sect­ing disks could be “ad­jus­ted” so that they be­came dis­joint. This would be pos­sible if the de­com­pos­i­tion space were \( \mathbb E^3 \). But Bing showed that that would lead to a con­tra­dic­tion, so that the de­com­pos­i­tion space does not sat­is­fy a “dis­joint disc” prop­erty and, hence, is not \( \mathbb E^3 \). The de­com­pos­i­tion space is, in fact, not a man­i­fold at any of the nonde­gen­er­ate “points.”

But Bing’s in­terest in the dog­bone space did not end with this achieve­ment. He was de­term­ined to un­der­stand the ex­tent to which the de­com­pos­i­tion ele­ments were linked, and what del­ic­ate prop­er­ties of 3-space were in­volved. What he proved (in a pa­per [10] that is most dif­fi­cult to read, even though it is ex­cel­lently writ­ten) was that the Cartesian product of the dog­bone space and a line is \( \mathbb E^4 \). White­head had con­struc­ted a fam­ous ex­ample of a con­tract­ible open sub­set of \( \mathbb E^3 \) which is not homeo­morph­ic to \( \mathbb E^3 \), and Arnold Sha­piro had re­cently shown that the product of this space with a line is \( \mathbb E^4 \). This was start­ling: \( \mathbb E^4 \) had factor­ings oth­er than \( \mathbb E^1 \times \mathbb E^3 \) and \( \mathbb E^2 \times \mathbb E^2 \). What Bing showed was that the dog­bone space was a factor of \( \mathbb E^4 \). In oth­er words, \( \mathbb E^4 \) has non-man­i­fold factors. The proof in­volved a very elab­or­ate ap­plic­a­tion of the shrink­ing cri­terion.

These three pa­pers were of fun­da­ment­al im­port­ance in the de­vel­op­ment of three-di­men­sion­al to­po­logy, but they also con­tained some of the sem­in­al ideas that were at the heart of the great ac­com­plish­ments of high­er-di­men­sion­al geo­met­ric to­po­logy of the late 1970s: de­com­pos­i­tion spaces, shrink­ing cri­ter­ia, sta­bil­iz­a­tion of de­com­pos­i­tion spaces (that is, non-man­i­fold de­com­pos­i­tion spaces whose product with \( \mathbb E^n \) were Eu­c­lidean), and the dis­joint-disk prop­erty. In Mi­chael Freed­man’s Veblen Prize speech, he pays trib­ute to the crit­ic­al role that Bing’s de­com­pos­i­tion the­ory played in Freed­man’s solu­tion of the four-di­men­sion­al Poin­caré Con­jec­ture. “Bing shrink­ing” played a key role in Torun­czyk’s work in \( Q \)-man­i­folds. In­ter­est­ingly, one of his the­or­ems (An ANR in Hil­bert space is a man­i­fold if and only if it has the “dis­crete-cells prop­erty”) not only uses Bing shrink­ing, but is re­min­is­cent of Bing’s “col­lec­tion­wise nor­mal” con­di­tion. Can­non and Ed­wards have giv­en us a mar­velous view of high­er-di­men­sion­al man­i­folds. As they have ac­know­ledged, they too were stand­ing on Bing’s shoulders.

Al­though Bing’s primary con­cern was to re­main with the to­po­logy of \( \mathbb E^3 \), he kept a lively in­terest in all areas of geo­met­ric to­po­logy and con­tinua the­ory.

One of the res­ults of the renais­sance of in­fin­ite-di­men­sion­al to­po­logy in the 1960s was the solu­tion of a prob­lem that went back at least 40 years: Is real Hil­bert space homeo­morph­ic to the count­able in­fin­ite product of real lines? The prob­lem was ex­pli­citly raised by both Frechet and Banach in their fam­ous books. Al­though the ques­tion must have aris­en count­lessly in classrooms, there seems to have been little pro­gress to­ward its solu­tion be­fore 1960. Fi­nally, in 1966, R. D. An­der­son gave an af­firm­at­ive solu­tion. It was a cul­min­a­tion of the work of sev­er­al au­thors, not­ably An­der­son, Bessaga, Ka­dec, and Pel­cyn­sky.

Bing, of course, was very in­ter­ested in un­der­stand­ing a proof of this the­or­em, and in 1968 An­der­son and Bing pub­lished a self-con­tained and com­pletely ele­ment­ary proof of this res­ult. The pa­per ap­peared in its en­tirety in the Bul­let­in of the A.M.S., upon in­vit­a­tion of the ed­it­ors [18].

The mono­tone-map­ping prob­lem was an­oth­er highly re­spec­ted prob­lem. In 1959, Why­burn had proved that if a map takes \( \mathbb E^2 \) to \( \mathbb E^2 \) and the in­verse of each point is com­pact and con­nec­ted, then the in­verse of each com­pact set is ne­ces­sar­ily com­pact. He asked wheth­er the same res­ult is true for \( \mathbb E^n \). In 1969, Glaser gave a neg­at­ive an­swer for \( n > 3 \). Later in the same year, Bing [20] gave a dif­fi­cult and in­geni­ous counter­example for the case \( n = 3 \).

Of course, fixed-point prob­lems are nev­er far from the heart of geo­met­ric to­po­lo­gists, and Bing made a sig­ni­fic­ant con­tri­bu­tion in this area, without ever pub­lish­ing a re­search pa­per to my know­ledge. He did pub­lish an ex­pos­it­ory pa­per in the Amer­ic­an Math Monthly in 1969, called “The elu­sive fixed point prop­erty” [19]. Re­view­ing 23 the­or­ems and rais­ing twelve ques­tions, it is a mod­el of ex­pos­i­tion. Each of the ques­tions sub­sequently has re­ceived at­ten­tion in the lit­er­at­ure, and one meth­od cas­u­ally em­ployed by Bing, the “dog chases rab­bit” tech­nique, has been ex­ploited fre­quently and fruit­fully, by Hagopi­an, for ex­ample.

Bing’s ex­pos­it­ory style is an im­port­ant part of his math­em­at­ic­al “work.” It is al­ways in­form­al, while in­tensely rig­or­ous. The proofs do not cov­er the tracks of dis­cov­ery. Pa­pers will of­ten ex­plain (with ex­amples) why a cer­tain al­tern­at­ive path would run in­to trouble. The title is of­ten the main res­ult. Bing’s lec­tur­ing style, his ex­pos­it­ory style, and his con­ver­sa­tion­al style were dis­arm­ingly geared to­ward clar­ity of thought and sim­pli­fic­a­tion of ex­pos­i­tion. His Col­loqui­um book [21] re­flects this qual­ity. Read­ing it, one has the feel­ing of a con­ver­sa­tion with the au­thor. Bing’s per­sona leaps out of the pages.

In con­clu­sion I would like to share with you some quo­ta­tions that I have gleaned in pre­par­ing this talk.

• Bing, “The pseudo-arc,” 1955: “The set of all bounded con­tinua (as arcs, discs, spheres points, etc.) that dif­fer from the pseudo-arc is only of the first cat­egory. This be­ing the case, if a per­son deal­ing with a con­tinuum whose shape is un­known (as a phys­i­cist deal­ing with one of the ob­sol­ete treat­ments of the atom), it might be more reas­on­able to sus­pect it to be in the shape of a pseudo-arc than to sus­pect it to be spher­ic­al.”
• Bing, “De­com­pos­i­tions of \( \mathbb E^3 \),” 1965: “I had hoped that oth­ers writ­ing about the dog­bone space would give a more el­eg­ant proof that it was to­po­lo­gic­ally dif­fer­ent from \( \mathbb E^3 \). Sev­er­al have not availed them­selves of this op­por­tun­ity.”
• Bing, “The mono­tone map­ping prob­lem,” 1965: “Per­haps \( \mathbb E^3 \) sheds more light on \( \mathbb E^n \) than \( \mathbb E^n \) sheds on \( \mathbb E^3 \).”
• Mi­chael Freed­man, Veblen prize ac­cept­ance speech, 1986: “But I owe a spe­cial debt to Bob Ed­wards, who taught me the branch of geo­metry, ‘Bing to­po­logy,’ which plays a cent­ral role in the work which the A.M.S. has re­cog­nized with this re­ward.”
• J. W. Can­non, I.C.M. Hel­sinki, 1978: “We ex­plained our work to Bing. He was not ex­cited. He found the proof ob­scure. In frus­tra­tion we sought the simplest pos­sible con­cep­tu­al frame­work en­com­passing the mildly wild 1-ulc tam­ing prop­er­ties, and the dis­joint disk de­com­pos­i­tion prop­er­ties be­came clear in our minds and the char­ac­ter­iz­a­tion con­jec­ture im­me­di­ately took its present form.”
• Bing, “What to­po­logy is here to stay”, 1955: “As to­po­logy grows we should grow with it. We should con­tin­ue to learn new meth­ods of at­tack and new res­ults. This does not mean that we should flip-flop from one field of math­em­at­ics to an­oth­er, try­ing to find something easy to do. The river that cuts a deep fur­row, that leaves a last­ing im­pres­sion, is one that fol­lows a steady course and does not me­ander all over the map.

  Those of us who are to be suc­cess­ful in re­search must re­main stu­dents. Our uni­versit­ies are turn­ing out too high a per­cent­age of “fin­ished products”… people whose train­ing is fin­ished when they gradu­ate… Per­haps it is more im­port­ant to provide stu­dents with the abil­ity and stim­u­lus to be act­ive re­search­ers than that it give them a broad back­ground.”

R H Bing’s con­tri­bu­tion to re­search was em­in­ent, and in­her­ent in that em­in­ence is that teach­ing was nev­er far from his mind, and he was a great teach­er. Those of us who are his stu­dents, his col­leagues, his math­em­at­ic­al friends, all share the be­ne­fits of that great­ness.