by Loring W. Tu
Raoul Bott passed away on December 20, 2005. In a career spanning five decades, Raoul Bott has wrought profound changes on the landscape of geometry and topology. It is a daunting task to improve upon his own reminiscences [22], [24], [17] and commentaries on papers [23], [25], [26], [27], punctuated as they are by insight, colorful turns of phrases and amusing anecdotes. This article is an updated reprint of one that first appeared in the book The founders of index theory: Reminiscences of Atiyah, Bott, Hirzebruch, and Singer (edited by S.-T. Yau, International Press, 2003). Taking a personal interest in the project, Raoul Bott introduced me to some of his friends and gave me access to his files. After the original article was completed in June 2000, he read it and verified the essential correctness of the accounts of both his life and his works. In the interest of preserving its official imprimatur as an authorized biography, the only changes I made to the 2003 version consist of this introductory paragraph, an update of the awards he received, and the suppression of a bibliography of his works not referenced in the article.
Early years
Raoul Bott was born in Budapest in 1923. His lineage fully reflects the geopolitical complexity of the region at the time. His mother’s family was Hungarian and Jewish, while his father’s side was Austrian and Catholic. His parents divorced soon after his birth, so he grew up with his mother and stepfather. Raised as a Catholic, Raoul spent his childhood and adolescence in Slovakia, which seventy years later, after alternating between Hungary and Czechoslovakia, is today an independent country.
In the first five years of school Raoul was not a good student. This should give comfort to all parents of late bloomers. In fact, he did not earn a single A except in singing and in German. Nonetheless, he showed an early talent for breaking rules and for generating sparks — electrical sparks, that is, rigged up with wires, fuse boxes, vacuum tubes, and transformers. The schools were formal and strict, and one could get slapped or have one’s ears pulled for misbehaving. For a budding original thinker, Raoul survived the schools relatively unscathed. He recalls a friar hitting him on the hand once and a teacher cuffing his ear another time, for horsing around too much.
It was by all accounts an idyllic existence, complete with a family villa, English governesses, and music lessons. This world came to an abrupt halt in 1935, when his mother died of cancer. In time his stepfather remarried.
Raoul’s experimental talent found its full flowering in adolescence. He and a kindred spirit Tomy Hornak built a small box with a slit for coins. When someone dropped a coin through the slit, a display lit up saying “Thank you.” In this way they funded their early experiments.
Raoul struggled with some subjects in school, and a tutor was hired to help him a few hours a week in his house. At the time Raoul and Tomy had built a gadget to communicate by Morse code. As he was being tutored, he would hold the gadget under the table and Tomy would be sitting in the basement. Raoul received the code by getting short and long electric shocks in his hand. He then responded by pressing a button to light up a bulb in the basement. While the tutor believed that his student was listening intently to the lesson, Raoul was chatting away in Morse code under the table. In retrospect, Bott calls this his first attempt at e-mail.
Canada
In 1938, with Hitler’s ascendancy and Germany’s march into Czechoslovakia, Bott’s stepparents flew him to the safety of England and enrolled him in an English boarding school. Since they had only transit visas for England, the following year they headed for Canada, a country that to this day has been extraordinarily welcoming to refugees and immigrants from around the world.
In the fall of 1941, after a rigorous year of preparatory studies in Ontario, Raoul Bott found himself at McGill University in Montreal. Given his electrical know-how, he chose, not surprisingly, electrical engineering as his major. His grades were respectable, but as he recalls in [24], he was more interested in upholding the “engineering tradition of hard drinking, loud, boisterous, mischievous, and macho behavior.” Mathematics was his best subject; still, it was mathematics in the engineering sense, not the kind of pure reasoning for which he became so well known years later.
With his European flair, his 6 ft. 2 in. frame, and the conspicuous fur cap he often wore, Bott stood out from the crowd at McGill. When friends asked him where he was from, he said from Dioszeg, Czechoslovakia, and he added facetiously, where he “was a count.” After that, everyone called him the Count.
The Count sometimes spoke a very foreign tongue. In the streetcars of Montreal, Raoul and his roommate Rodolfo Gurdian would occasionally engage in a deliberately loud and animated conversation. Nothing they said made sense, for they were making up the language as they went along. From the corners of their eyes, they enjoyed watching the quizzical expressions on the faces of the surrounding passengers, who were trying hard to figure out what language the two of them were speaking.
Bott loved the opera, but as a penniless student how was he to afford it? One time the famous tenor Ezio Pinza came to sing in His Majesty’s Theater, the opera house of Montreal in the Forties. For this occasion, Bott dressed up in his Sunday best and went to the theater. When the man at the entrance stopped him, Bott told him he couldn’t do this because he was Ezio Pinza’s nephew. Bott said it with such assurance that the man let him in. After that, Bott could go to all the shows at this theater for free.
Bott’s roommate Rodolfo, equally penniless, also loved the opera. But Rodolfo did not have the nerve to sneak into the theater. When the opera “Carmen” was playing, Rodolfo was very eager to attend. Bott magnanimously invited him. By then, the ticket-taker knew Bott very well, but he stopped Rodolfo at the entrance. Bott turned around and intoned in his authoritative voice, “It’s all right. He can come in.” Without any hesitation the ticket taker obeyed the order of this “nephew” of Ezio Pinza.
One New Year’s Day, Raoul, Rodolfo, and some friends went to Mont Tremblant, a winter resort north of Montreal. In the most prominent and expensive hotel, a big celebration was going on. Somehow, to the envy of his friends, Raoul sneaked in. A little later, Raoul was standing on the balcony, looking down contemptuously at his friends and showing them a chicken leg he was eating. After he finished it, he threw the bone, with disdain, to his hungry friends.
(Old habits die hard. In 1960, Bott, by then a full professor at Harvard, was in India with Michael Atiyah, both giving lectures as guests of the Tata Institute of Mathematics. One day, as they walked in the streets of New Dehli, they passed by a big celebration. Bott decided to slip in uninvited, dragging Atiyah along with him. Atiyah, a professor at Oxford who was later anointed Sir Michael by the Queen and elected President of the Royal Society, was at first discomfited, but soon joined whole-heartedly in the festivities. They had a rousing time, sharing in the general merriment of complete strangers.)
Upon graduation, Bott joined the army, but the atomic bomb at Hiroshima put an end to his military career after only four months. He entered a one-year master’s program in the Engineering Department at McGill. Gradually it dawned on him that his interest lay more in mathematics than in engineering, and he produced a very mathematical master’s thesis on “impedance matching,” which he said, “the department accepted with some misgivings and about whose mathematical rigor I have doubts to this very day.”
At McGill, Raoul met his future wife, Phyllis, an English-literature major from the West Indies. Today, Phyllis remembers Raoul’s first marriage proposal. At the time he was doing his short stint in the army. In full uniform, he said, “Would you marry me? Because if you do, the army will pay me more money.” And then pointing through the window to his little room, he added, “And we could be living there.” The proposal was not accepted. But two years later, they married. The Botts have been together ever since, and now have four children and eight grandchildren. They celebrated their golden anniversary in 1997.
Sermon
While in the master’s program in engineering at McGill, Bott floundered in trying to decide on the general direction of his career. Thirty years later, Bott was asked to deliver a sermon at Harvard’s Memorial Chapel. As he discussed the biblical passage of Eli, the wise man who counseled the young Samuel (1 Samuel 3:3–6, 8–10), he reflected on the pivotal moment in his life that launched his mathematical career. His description of his own Eli deserves to be read in the original:
And so when I saw the two readings we just heard juxtaposed in a Scripture Service, I could not resist them. For they are appropriate to all of us, whether called to high causes or to lowly ones. And they are maybe especially appropriate to the young people of today in their search of their destiny.
For surely there never has been a time when our young people have been given such freedom and therefore such responsibility to find this destiny.
But how are we to know where we are called? And how are we to know who is calling us? These are questions beyond a mathematician’s ken. There are some who seem to have perfect pitch in these matters. There are many more who might think that they have. But with most of us, it is as it was with Samuel, and we are then truly blessed to have an advisor such as Eli. He stands for all of us Teachers as an example. For apart from communicating our call to our students, we should try and help them above all to discern theirs.
I well remember my Eli. He was the Dean of the Medical School at McGill and I approached him for help in entering the medical school there, when in 1945 the atomic bomb unexpectedly put an end to the war and to my four-month old career in the Canadian Infantry.
The Army very wisely decided to get rid of such green recruits as soon as possible, and so we all again found ourselves quite unexpectedly in charge of our own lives. I had graduated in engineering earlier that year but had already decided against that career.
The Dean greeted me very cordially and assured me that there was a great need for technically trained doctors. “But,” he said, seating me next to him, “first tell me a little about yourself. Did you ever have any interest in botany, say, or biology?” “Well, not really,” I had to admit. “How about chemistry” — “Oh, I hated that course.” And so it went. After a while he said, “Well, is it maybe that you want to do good for humanity?” And then, while I was coughing in embarrassment, he went on, “Because they make the worst doctors.”
I thanked him, and as I walked out of his door I knew that I would start afresh and with God’s grace try and become a mathematician.
Mathematical career
Initially Bott wanted to stay at McGill to do a mathematics Ph.D. Because of his sketchy background, however, the McGill Math Department recommended that he pursue a Bachelor’s degree in mathematics first. It would have taken another three years. Sensing his disappointment, Professor Williams of McGill then suggested Carnegie Tech (now Carnegie-Mellon University) to Bott, where John Synge was just forming a new graduate program and would need some students.
Synge received Bott warmly at Carnegie Tech, but as they read the rules of the program together, they found that Bott would have to spend three years taking courses in the newly minted master’s program. In a flash of inspiration, Synge said, “Let’s look at the Ph.D. program.” It turned out to have hardly any requirements at all! Normally the master’s program is a prerequisite to the Ph.D. program, but perhaps recognizing a special gift in Bott, Synge put him in the Ph.D. program. In just two years Bott would walk out with his degree.
Bott found the Carnegie Tech atmosphere exceedingly supportive. The small coterie of mathematics students included Hans Weinberger, now at the University of Minnesota, and John Nash, an advanced undergraduate who after a thirty-year battle with schizophrenia received the Nobel prize in 1994. In later years Bott said of Carnegie Tech, “Being a brand new graduate program, they hadn’t learned yet how to put hurdles in front of graduate students.” Bott considers himself very fortunate to have an advisor in R. J. Duffin, for Duffin treated him as an equal from the very outset and together they published two papers on the mathematics of electrical networks.
The first of these two papers, on impedance functions [1], so impressed Hermann Weyl that he invited Bott to the Institute for Advanced Study in 1949. Thus began Bott’s initiation into the mysteries of algebraic topology. Apart from Weyl, among his main teachers were N. Steenrod, E. Specker, K. Reidemeister, and M. Morse. Of Ernst Specker, Bott said in [18], “I bombarded Ernst with so many stupid questions that in desperation he finally imposed a fine of 25 cents on any conjecture he could disprove in less than five minutes. This should give you some idea of the inflation of the past thirty years, and also help to explain Ernst’s vast fortune at this time.”
At the time Norman Steenrod was writing his classic book on the topology of fiber bundles, and teaching a course based on it. This course greatly influenced Bott’s mathematical development.
Bott describes Steenrod with admiration as someone who treated high and low alike, with equal respect. At Princeton, the graduate students could be intimidating, because they knew so much, and they let you know it. Steenrod, on the other hand, was different. In spite of his stature in the mathematical community, he put everyone at ease. In seminars Steenrod did not hesitate to ask the most basic questions. This was quite often a boon to the others in the audience, too intimidated and too befuddled to ask the questions themselves.
After two years at the Institute, Bott went to the University of Michigan. In 1959 he became a professor at Harvard, where he has remained since. In 1999 Bott formally retired from teaching. He is now William Casper Graustein Research Professor at Harvard.
Dunster House
An unusual item in the curriculum vitae of Raoul Bott, for a mathematician at least, was his tenure as the Master of Dunster House in 1978–84. At Harvard the undergraduates live in social units called “Houses,” modelled somewhat after the Colleges at Oxford and Cambridge. A House is more than a place to sleep; it is a way to create a sense of a small community within a large university. Each House has its own dining hall, dormitories, social activities, and a staff headed by a Master. The academic staff consists of a bevy of resident and non-resident tutors.
Whether out of a lack of interest or a perceived mismatch of temperament, pure mathematicians are rarely called to be Masters of the undergraduate Houses. In 1978, in a break with tradition, the President of Harvard University appointed Bott the Master of Dunster House. This entailed living in the Master’s Residence in the midst of three hundred undergraduates. Bott’s gregariousness was a good match for the post.
Every year the Houses compete in a water-raft race on the Charles River. This is no gentleman’s canoe race as practiced in England. In the Harvard version, attacks on other Houses’ rafts are condoned, even encouraged. One year the Lowell House team had its Master at the helm, resplendent in an admiral’s hat. Bott, commanding the Dunster House armada, saw the beautiful hat. He hollered, “Get me that hat!” Now, this is the sort of order undergraduates love to obey. In no time the Dunster students had paddled to the Lowell raft. A struggle ensued, and like any good pirates, the Dunster contingent captured the admiral’s hat. It was later hung, as a trophy, high in the ceiling of the Dunster House dining hall.
Showing true House spirit, the Dunster House crew team had its official team T-shirt emblazoned with “Dunster House,” a pair of oars, and the exhortation: “Raoul, Raoul, Raoul your Bott.”
The Harvard Houses have counterparts at Yale, where they are called Colleges. A friendly rivalry has always existed between these two august institutions, and it extends to the Houses and Colleges. Some of the Houses at Harvard even have “sister Colleges” with which they are loosely affiliated. They would, for example, visit each other during the Harvard–Yale football games.
In the aftermath of the Sixties, many of the traditions at the Ivy League universities, such as the dress code and the parietal rules, have gone by the wayside, and for a number of years Dunster House had not had contact with Berkeley College, its sister College at Yale. One year the Berkeley College Master, a distinguished historian, decided to revive the tradition. He wrote to Bott suggesting a visit to Dunster House during the weekend of the Harvard–Yale football game. Bott readily agreed, but decided to make the occasion a memorable one. Why not fool the Yalies into thinking that Harvard has kept up, at least to a certain point, the Oxbridge tradition of high table and academic gowns at dinner? Why not show that, perhaps, Dunster House was more “civilized” than its Yale counterpart? With enthusiasm, the Dunster House undergraduates all supported the idea.
On the appointed day, the Dunster House dining hall was transformed from a cafeteria into a hallowed hall, complete with linen, waiters and waitresses, and even a wine steward wearing a large medal. Unlike on a normal day, there were no T-shirts or cut-offs in sight. Every tutor was attired in a black academic gown. An orchestra sat in waiting. When the Yale Master and his tutors arrived, Bott asked, with a straight face, “Where are your gowns?” Of course, they didn’t have any. “Well, no problem, you could borrow some of ours.” So the Dunster tutors led them to some gowns that had just been lent from Harvard’s Chapel. As Bott entered the Dining Hall with his guests, trumpets blared forth and the orchestra started playing. The undergraduates were already seated, looking prim, proper, and serious. Bott and his tutors dined with the Yale visitors at a high table, on a stage especially set up for this occasion. The orchestra serenaded the diners with music. Everything went according to plan. But the Yale Master, ever sharp, had the last laugh. He opened his speech by saying, “I’m glad to see that culture has finally migrated from New Haven to Harvard.”
Bott as a teacher
Bott’s lectures are legendary for their seeming ease of comprehension. His style is typically the antithesis of the definition-theorem-proof approach so favored among mathematical speakers. Usually he likes to discuss a simple key example that encapsulates the essence of the problem. Often, as if by magic, a concrete formula with transparent significance appears.
At a reception for new graduate students at Harvard, he once shared his view of the process of writing a Ph.D. thesis. He said it is like doing a homework problem; it’s just a harder problem. You try to understand the problem thoroughly, from every conceivable angle. Much of the thesis work is perseverance, as opposed to inspiration. Above all, “make the problem your own.”
Many of his students testify to his warmth and humanity, but he also expects the students to meet an exacting standard. He once banned the word “basically” from an advisee’s vocabulary, because that word to Bott signifies that some details are about to be swept under a rug.
This insistence on thoroughness and clarity applies to his own work as well. I. M. Singer remarked that in their younger days, whenever they had a mathematical discussion, the most common phrase Bott uttered was “I don’t understand,” and that a few months later Bott would emerge with a beautiful paper on precisely the subject he had repeatedly not understood.
Seminar speakers at Harvard tend to address themselves to the experts in the audience. But like Steenrod, Bott often interrupts the speakers with the most basic questions, with the salutary effect of slowing down the speakers and making them more intelligible to lesser mortals.
At Michigan and Harvard, Bott directed over 36 Ph.D. theses. Some of his students have become luminaries in their own right: Stephen Smale and Daniel Quillen received the Fields Medal in 1966 and 1978 respectively, and Robert MacPherson the National Academy of Science Award in Mathematics in 1992.
A complete list of his students can be found here.
Honors and awards
Throughout his career, Bott has been showered with honors, awards, and prizes. The more noteworthy awards include: Sloan Fellowship (1956–60), Veblen Prize of the American Mathematical Society (1964), Guggenheim Fellowship (1976), National Medal of Science (1987), Steele Prize for Lifetime Achievement of the American Mathematical Society (1990), and the Wolf Prize in Mathematics (2000).
He was twice invited to address the International Congress of Mathematicians, in Edinburgh in 1958 and in Nice in 1970.
He was elected Vice President of the American Mathematical Society in 1974–75, Honorary Member of the London Mathematical Society (1976), Honorary Fellow of St. Catherine’s College, Oxford (1985), Honorary Member of the Moscow Mathematical Society (1997), and Foreign Member of the Royal Society (2005). He has been a member of the National Academy of Science since 1964, and the French Academy of Sciences since 1995.
In 1987 he gave the Convocation Address at McGill University. He has also received Honorary Degrees of Doctor of Science from the University of Notre Dame (1980), McGill University (1987), Carnegie Mellon University (1989), and the University of Leicester, England (1995).
Mathematical works
The bibliography in Raoul Bott’s “Collected papers” [23], [25], [26], [27] lists his publications, with some omissions, up to 1990.
When asked to single out the top three, in the manner of an Olympic contest, he replied, “Can I squeeze in another one?” But after listing four as the tops, he sighed and said, “This is like being asked to single out the favorites among one’s children.” In the end he came up with a top-five list, in chronological order:
[6] Homogeneous vector bundles,
[7] The periodicity theorem,
[15] Topological obstruction to integrability,
[19] Yang–Mills equations over Riemann surfaces,
[20] The localization theorem in equivariant cohomology.
To discuss only these five would not do justice to the range of his output. On the other hand, it is evidently not possible to discuss every item in his ever-expanding opus. As a compromise, I asked him to make a longer list of all his favorite papers, without trying to rank them. What follows is a leisurely romp through the nineteen papers he chose. My goal is to explain, as simply as possible, the main achievement of his own favorite papers. For this reason, the theorems, if stated at all, are often not in their greatest generality.
Impedance
The subject of Raoul Bott’s first paper [1] dates back to his engineering days. An electrical network determines an impedance function \( Z(s) \), which describes the frequency response of the network. This impedance function \( Z(s) \) is a rational function of a complex variable \( s \) and is positive-real (p.r.) in the sense that it maps the right half-plane into itself. An old question in electrical engineering asks whether conversely, given a positive-real rational function \( Z(s) \), it is possible to build a network with \( Z(s) \) as its impedance function. In some sense O. Brune had solved this problem in 1931, but Brune’s solution assumes the existence of an “ideal transformer,” which in practice would have to be the size of, say, the Harvard Science Center. The assumption of an ideal transformer renders Brune’s algorithm not so practical, and it was Raoul’s dream at McGill to remove the ideal transformer from the solution.
At his first meeting with his advisor Richard Duffin at Carnegie Tech, he blurted out the problem right away. Many days later, after a particularly fruitless and strenuous discussion, Raoul went home and realized how to do it. He called Duffin. The phone was busy. As it turned out, Duffin was calling him with exactly the same idea! They wrote up the solution to the long-standing problem in a joint paper, which amazingly took up only two pages.
Morse theory
As mentioned earlier, the paper on impedance so impressed Hermann Weyl that he invited Bott to the Institute for Advanced Study at Princeton in 1949. There Bott came into contact with Marston Morse. Morse’s theory of critical points would play a decisive role throughout Bott’s career, notably in his work on homogeneous spaces, the Lefschetz hyperplane theorem, the periodicity theorem, and the Yang–Mills functional on a moduli space.
In the Twenties, Morse had initiated the study of the critical points of a function on a space and its relation to the topology of the space. A smooth function \( f \) on a smooth manifold \( M \) has a critical point at \( p \) in \( M \) if there is a coordinate system \( (x_1, \ldots, x_n) \) at \( p \) such that all the partial derivatives of \( f \) vanish at \( p \): \[ \dfrac{\partial f}{\partial x_i} (p) =0 \qquad \text{for all } i= 1,\ldots, n. \] Such a critical point is nondegenerate if the matrix of second partials, called the Hessian of \( f \) at \( p \), \[ H_p f= \left[ \dfrac{\partial^2 f}{\partial x_i \partial x_j}(p) \right], \] is nonsingular. The index \( \lambda (p) \) of a nondegenerate critical point \( p \) is the number of negative eigenvalues of the Hessian \( H_p f \); it is the number of independent directions along which \( f \) will decrease from \( p \).
If a smooth function has only nondegenerate critical points, we call it a Morse function. The behavior of the critical points of a Morse function can be summarized in its Morse polynomial: \[ \mathcal{M}_t(f) := \sum t^{\lambda (p)}, \] where the sum runs over all critical points \( p \).
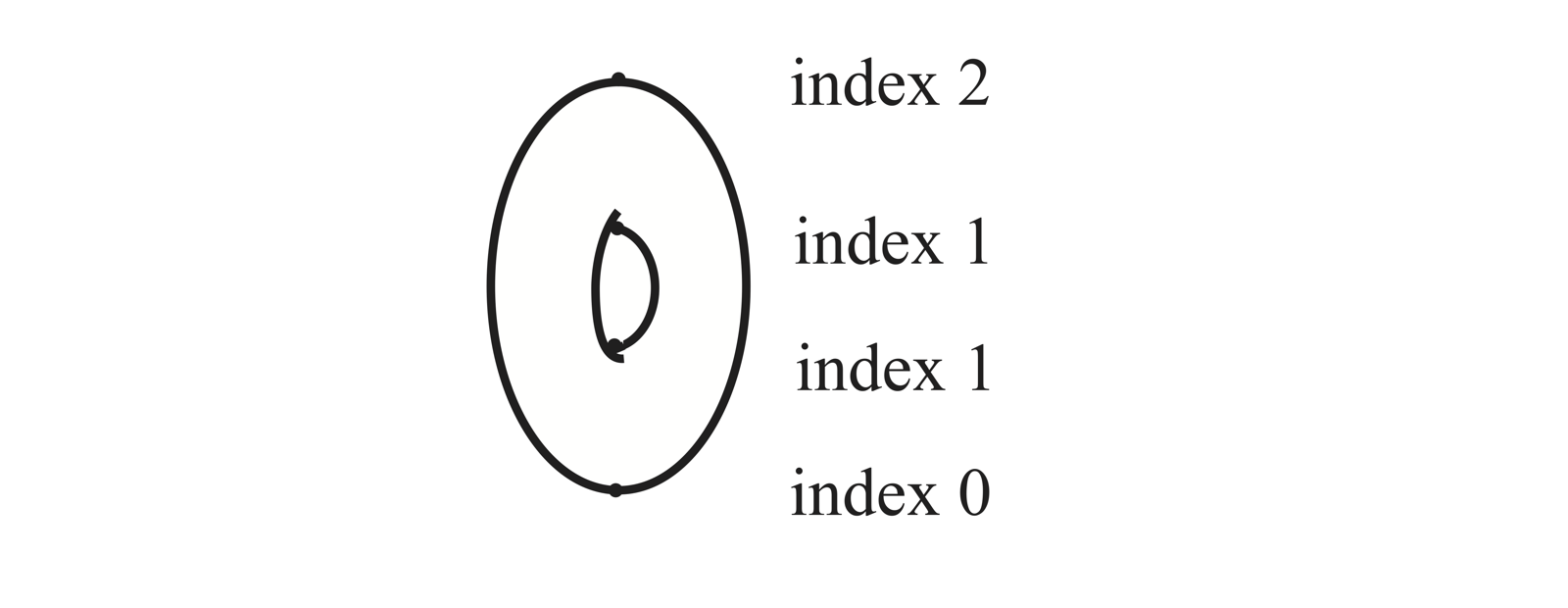
A typical example of a Morse function is the height function \( f \) of a torus standing vertically on a table top (see the figure). The height function on this torus has four critical points of index 0, 1, 1, 2 respectively. Its Morse polynomial is \[ \mathcal{M}_t (f) = 1 + 2t+t^2. \]
For a Morse function \( f \) on a compact manifold \( M \), the fundamental results of Morse theory hinge on the fact that \( M \) has the homotopy type of a CW complex with one cell of dimension \( \lambda \) for each critical point of \( f \) of index \( \lambda \). This realization came about in the early Fifties, due to the work of Pitcher, Thom, and Bott.
Two consequences follow immediately:
The weak Morse inequalities: \[ \#\{\text{critical points of index } i\} \ge i\text{-th Betti number}. \] If \[ P_t (M) = \sum \dim H_i(M)\, t^i \] is the Poincaré polynomial of \( M \), the Morse inequalities can be restated in the form \[ \mathcal{M}_t(f) \ge P_t(M), \] meaning that their difference \( \mathcal{M}_t(f) - P_t(M) \) is a polynomial with nonnegative coefficients. This inequality provides a topological constraint on analysis, for it says that the \( i \)-th Betti number of the manifold sets a lower bound on the number of critical points of index \( i \) that the function \( f \) must have.
The lacunary principle: If no two critical points of the Morse function \( f \) have consecutive indices, then \begin{equation} \label{perfect} \mathcal{M}_t(f) = P_t(M). \end{equation} The explanation is simple: since in the CW complex of \( M \) there are no two cells of consecutive dimensions, the boundary operator is automatically zero. Therefore, the cellular chain complex is its own homology.
A Morse function \( f \) on \( M \) satisfying \eqref{perfect} is said to be perfect. The height function on the torus above is a perfect Morse function.
Classical Morse theory deals only with functions all of whose critical points are nondegenerate; in particular, the critical points must all be isolated points. In many situations, however, the critical points form submanifolds of \( M \). For example, if the torus now sits flat on the table, as a donut usually would, then the height function has the top and bottom circles as critical manifolds (see the figure).

One of Bott’s first insights was to see how to extend Morse theory to this situation. In [2] he introduced the notion of a nondegenerate critical manifold: a critical manifold \( N \) is nondegenerate if at any point \( p \) in \( N \) the Hessian of \( f \) restricted to the normal space to \( N \) is nonsingular. The index \( \lambda (N) \) of the nondegenerate critical manifold \( N \) is then defined to be the number of negative eigenvalues of this normal Hessian; it represents the number of independent normal directions along which \( f \) is decreasing. For simplicity, assume that the normal bundles of the nondegenerate critical manifolds are all orientable. To form the Morse polynomial of \( f \), each critical manifold \( N \) is counted with its Poincaré polynomial; thus, \[ \mathcal{M}_t(f) := \sum P_t(N)\, t^{\lambda (N)}, \] summed over all critical manifolds.
With this definition of the Morse polynomial, Bott proved in [2] that if a smooth function \( f \) on a smooth manifold \( M \) has only nondegenerate critical manifolds, then the Morse inequality again holds: \[ \mathcal{M}_t(f) \ge P_t(M). \]
Lie groups and homogeneous spaces
In the Fifties, Bott applied Morse theory with great success to the topology of Lie groups and homogeneous spaces. In [3] he showed how the diagram of a compact semisimple connected and simply connected group \( G \) determines the integral homology of both the loop space \( \Omega G \) and the flag manifold \( G/T \), where \( T \) is a maximal torus.
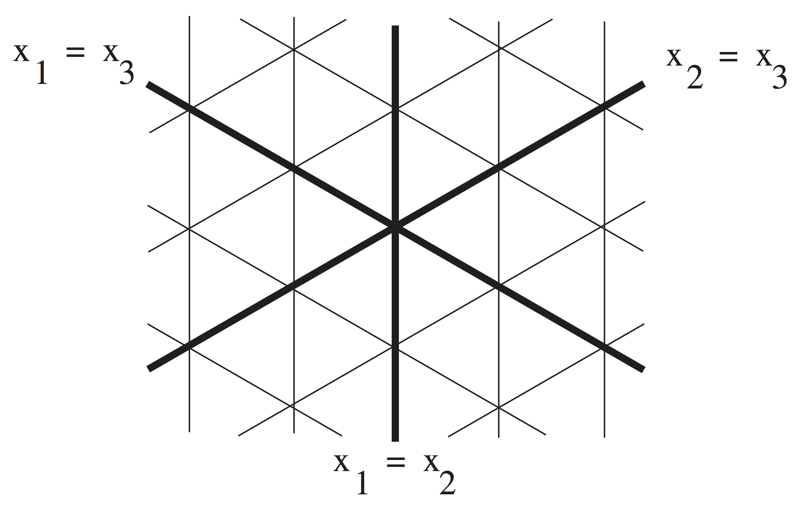
Indeed, Morse theory gives a beautiful CW cell structure on \( G/T \), up to homotopy equivalence. To explain this, recall that the adjoint action of the group \( G \) on its Lie algebra \( \mathfrak{g} \) restricts to an action of the maximal torus \( T \) on \( \mathfrak{g} \). As a representation of the torus \( T \), the Lie algebra \( \mathfrak{g} \) decomposes into a direct sum of irreducible representations \[ \mathfrak{g} = \mathfrak{t} \oplus \sum E_{\alpha} , \] where \( \mathfrak{t} \) is the Lie algebra of \( T \) and each \( E_{\alpha} \) is a 2-dimensional space on which \( T \) acts as a rotation \( e^{2\pi i \alpha (x)} \), corresponding to the root \( \alpha (x) \) on \( \mathfrak{t} \). The diagram of \( G \) is the family of parallel hyperplanes in \( \mathfrak{t} \) where some root is integral. A hyperplane that is the zero-set of a root is called a root plane.
For example, for the group \( G = \mathrm{SU} (3) \) and maximal torus \[ T=\left\{ \left. \begin{bmatrix} e^{2\pi i x_1} & & \\ & e^{2\pi i x_2} & \\ & & e^{2\pi i x_3} \end{bmatrix} \ \right| \ x_1+x_2+x_3 = 0, x_i \in \mathbb{R}\right\} . \] the roots are \( \pm(x_1 - x_2), \pm(x_1 - x_3) , \pm(x_2 - x_3) \), and the diagram is the collection of lines in the plane \( x_1+x_2+x_3=0 \) in \( \mathbb{R}^3 \) as in the figure. In this figure, the root planes are the thickened lines.
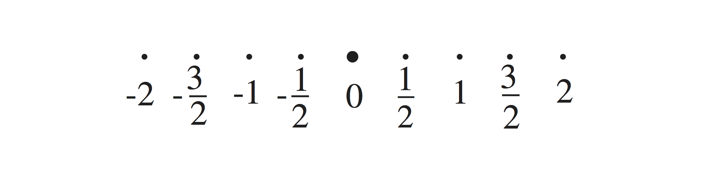
For \( G=\mathrm{SU} (2) \) and \[ T= \left\{ \left. \begin{bmatrix} e^{2\pi i x} & 0 \cr 0 & e^{-2\pi i x} \end{bmatrix} \ \right| \ x \in\mathbb{R}\right\}, \] the Lie algebra \( \mathfrak{t} \) is \( \mathbb{R} \), the roots are \( \pm 2x \), and the adjoint representation of of \( G \) on \( \mathfrak{g} = \mathbb{R}^3 \) corresponds to rotations. The root plane is the origin.
A point \( B \) in \( \mathfrak{t} \) is regular if its normalizer has minimal possible dimension, or equivalently if its normalizer is \( T \). It is well known that a point \( B \) in \( \mathfrak{t} \) is regular if and only if it does not lie on any of the hyperplanes of the diagram. If \( B \) is regular, then the stabilizer of \( B \) under the adjoint action of \( G \) is \( T \) and so the orbit through \( B \) is \( G/T \).
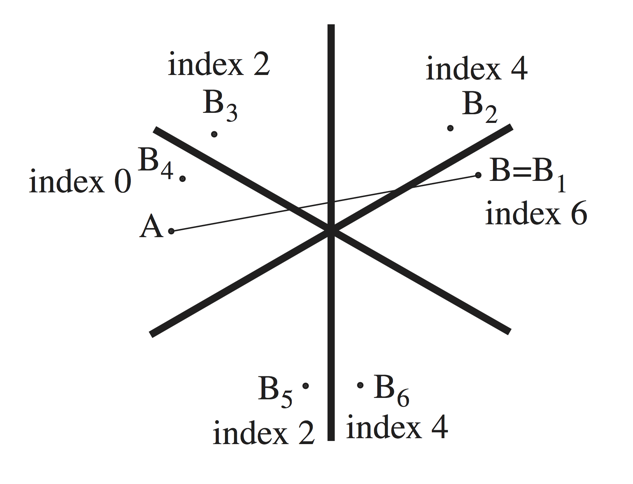
Choose another regular point \( A \) in \( \mathfrak{t} \) and define the function \( f \) on \[ \operatorname{Orbit} (B) = G/T \] to be the distance from \( A \); here, the distance is measured with respect to the Killing form on \( \mathfrak{g} \). Let \( \{ B_i\} \) be all the points in \( \mathfrak{t} \) obtained from \( B \) by reflecting about the root planes. Then Bott’s theorem asserts that \( f \) is a Morse function on \( G/T \) whose critical points are precisely all the \( B_i \)’s. Moreover, the index of a critical point \( B_i \) is twice the number of times that the line segment from \( A \) to \( B_i \) intersects the root planes. This cell decomposition of Morse theory fits in with the more group-theoretic Bruhat decomposition.
For \( G=\mathrm{SU} (3) \) and \( T \) the set of diagonal matrices in \( \mathrm{SU}(3) \), the orbit \( G/T \) is the complex flag manifold \( \operatorname{Fl} (1,2,3) \), consisting of all flags \[ V_1 \subset V_2 \subset \mathbb{C}^3, \qquad \dim_{\mathbb{C}} V_i = i. \] Bott’s recipe gives 6 critical points of index \( 0,2,2,4,4,6 \) respectively on \( G/T \) (See the figure). By the lacunary principle, the Morse function \( f \) is perfect. Hence, the flag manifold \( \operatorname{Fl} (1,2,3) \) has the homotopy type of a CW complex with one 0-cell, two 2-cells, two 4-cells, and one 6-cell. Its Poincaré polynomial is therefore \[ P_t(\operatorname{Fl} (1,2,3)) = 1+2t^2 +2t^4 +t^6. \]
Index of a closed geodesic
For two points \( p \) and \( q \) on a Riemannian manifold \( M \), the space \( \Omega_{p,q}(M) \) of all paths from \( p \) to \( q \) on \( M \) is not a finite-dimensional manifold. Nonetheless, Morse theory applies to this situation also, with a Morse function on the path space \( \Omega_{p,q} \) given by the energy of a path: \[ E(\mu )=\int_a^b \Bigl\langle \frac{d\mu}{dt}, \frac{d\mu}{dt} \Bigr\rangle\, dt. \] The first result of this infinite-dimensional Morse theory asserts that the critical points of the energy function are precisely the geodesics from \( p \) to \( q \).
Two points \( p \) and \( q \) on a geodesic are conjugate if keeping \( p \) and \( q \) fixed, one can vary the geodesic from \( p \) to \( q \) through a family of geodesics. For example, two antipodal points on an \( n \)-sphere are conjugate points. The multiplicity of \( q \) as a conjugate point of \( p \) is the dimension of the family of geodesics from \( p \) to \( q \). On the \( n \)-sphere \( \mathbb{S}^n \), the multiplicity of the south pole as a conjugate point of the north pole is therefore \( n-1 \).
If \( p \) and \( q \) are not conjugate along the geodesic, then the geodesic is nondegenerate as a critical point of the energy function on \( \Omega_{p,q} \). Its index, according to the Morse index theorem, is the number of conjugate points from \( p \) to \( q \) counted with multiplicities.
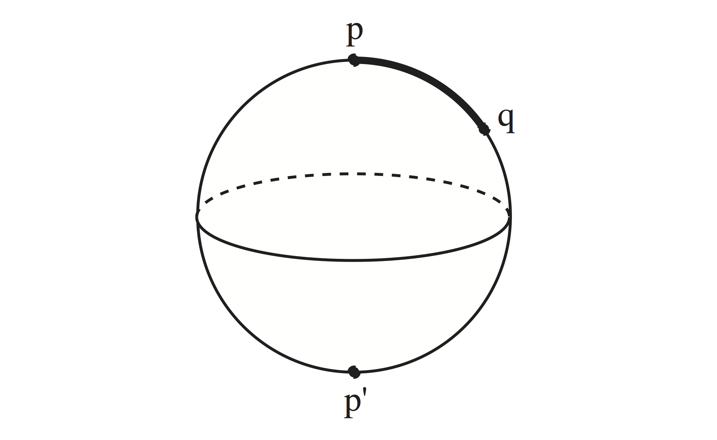
On the \( n \)-sphere let \( p \) and \( p^{\prime} \) be antipodal points and \( q \ne p^{\prime} \). The geodesics from \( p \) to \( q \) are \( pq \), \( pp^{\prime}q \), \( pqp^{\prime}pq \), \( pp^{\prime}qpp^{\prime}q \), …, of index \( 0, n-1 \), \( 2(n-1) \), \( 3(n-1), \dots \), respectively. By the Morse index theorem, the energy function on the path space \( \Omega_{p,q}(\mathbb{S}^n) \) has one critical point each of index \( 0, n-1 \), \( 2(n-1) \), \( 3(n-1), \dots \). It then follows from Morse theory that \( \Omega_{p,q}(\mathbb{S}^n) \) has the homotopy type of a CW complex with one cell in each of the dimensions \( 0, n-1 \), \( 2(n-1) \), \( 3(n-1), \dots \).
Now consider the space \( \Omega M \) of all smooth loops in \( M \), that is, smooth functions \( \mu: \mathbb{S}^1 \to M \). The critical points of the energy function on \( \Omega M \) are again the geodesics, but these are now closed geodesics. A closed geodesic is never isolated as a critical point, since for any rotation \( r: \mathbb{S}^1 \to \mathbb{S}^1 \) of the circle, \( \mu \circ r: \mathbb{S}^1 \to M \) is still a geodesic. In this way, any closed geodesic gives rise to a circle of closed geodesics. When the Riemannian metric on \( M \) is generic, the critical manifolds of the energy function on the loop space \( \Omega \) will all be circles.
Morse had shown that the index of a geodesic is the number of negative eigenvalues of a Sturm differential equation, a boundary-value problem of the form \( Ly=\lambda y \), where \( L \) is a self-adjoint second-order differential operator. For certain boundary conditions, Morse had expressed the index in terms of conjugate points, but this procedure does not apply to closed geodesics, which correspond to a Sturm problem with periodic boundary conditions.
In [5] Bott found an algorithm to compute the index of a closed geodesic. He was then able to determine the behavior of the index when the closed geodesic is iterated. Bott’s method is in fact applicable to all Sturm differential equations. And so in his paper he also gave a geometric formulation and new proofs of the Sturm–Morse separation, comparison, and oscillation theorems, all based on the principle that the intersection number of two cycles of complementary dimensions is zero if one of the cycles is homologous to zero.
Homogeneous vector bundles
Let \( G \) be a connected complex semisimple Lie group, and \( P \) a parabolic subgroup. Then \( G \) is a principal \( P \)-bundle over the homogeneous manifold \( X= G/P \). Any holomorphic representation \( \varphi : P \to \operatorname{Aut} (E) \) on a complex vector space \( E \) induces a holomorphic vector bundle \( \mathbb{E} \) over \( X \): \[ \mathbb{E}:= G \times_{\varphi} E := (G \times E)/ \sim, \] where \( (gp,e)\sim (g, \varphi(p) e) \). Then \( \mathbb{E} \) is a holomorphic vector bundle over \( X= G/P \). A vector bundle over \( X \) arising in this way is called a homogeneous vector bundle. Let \( \mathcal{O} (\mathbb{E}) \) be the corresponding sheaf of holomorphic sections. The homogeneous vector bundle \( \mathbb{E} \) inherits a left \( G \)-action from the left multiplication in \( G \): \[ h.(g,e)=(hg, e) \quad\quad \text{for } h,g \in G, e \in E. \] Thus, all the cohomology groups \( H^q(X, \mathcal{O}(\mathbb{E})) \) become \( G \)-modules.
In [6] Bott proved that if the representation \( \varphi \) is irreducible, the cohomology groups \( H^q(X, \mathcal{O}(\mathbb{E})) \) all vanish except possibly in one single dimension. Moreover, in the nonvanishing dimension \( q \), \( H^q(X, \mathcal{O}(\mathbb{E})) \) is an irreducible representation of \( G \) whose highest weight is related to \( \varphi \).
This theorem generalizes an earlier theorem of Borel and Weil, who proved it for a positive line bundle.
In Bott’s paper one finds a precise way of determining the nonvanishing dimension in terms of the roots and weights of \( G \) and \( P \). Thus, on the one hand, Bott’s theorem gives a geometric realization of induced representations, and on the other hand, it provides an extremely useful vanishing criterion for the cohomology of homogeneous vector bundles.
The periodicity theorem
Homotopy groups are notoriously difficult to compute. For a simple space like the \( n \)-sphere already, the higher homotopy groups exhibit no discernible patterns. It was therefore a complete surprise in 1957 when Raoul Bott computed the stable homotopy groups of the classical groups and found a simple periodic pattern for each of the classical groups [7].
We first explain what is meant by the stable homotopy group. Consider the unitary group \( U(n+1) \). It acts transitively on the unit sphere \( \mathbb{S}^{2n+1} \) in \( \mathbb{C}^{n+1} \), with stabilizer \( U(n) \) at the point \( (1,0,\dots,0) \). In this way, the sphere \( \mathbb{S}^{2n+1} \) can be identified with the homogeneous space \( U(n+1)/U(n) \), and there is a fibering \( U(n+1) \to \mathbb{S}^{2n+1} \) with fiber \( U(n) \). By the homotopy exact sequence of a fibering, the following sequence is exact: \[ \cdots \to \pi_{k+1}(\mathbb{S}^{2n+1}) \to \pi_k (U(n)) \to \pi_k (U(n+1)) \to \pi_k (\mathbb{S}^{2n+1}) \to \cdots. \] Since \( \pi_k (\mathbb{S}^m) = 0 \) for \( m > k \), it follows immediately that as \( n \) goes to infinity (in fact for all \( n > k/2 \)), the \( k \)-th homotopy group of the unitary group stabilizes: \[ \pi_k (U(n)) = \pi_k (U(n+1)) = \pi_k(U(n+2)) = \cdots. \] This common value is called the \emph{\( k \)-th stable homotopy group} of the unitary group, denoted \( \pi_k (U) \).
In the original proof of the periodicity theorem [7], Bott showed that in the loop space of the special unitary group \( \mathrm{SU}(2n) \), the manifold of minimal geodesics is the complex Grassmannian \[ G(n,2n) =\frac{U(2n)}{U(n)\times U(n)}. \] By Morse theory, the loop space \( \Omega \mathrm{SU} (2n) \) has the homotopy type of a CW complex obtained from the Grassmannian \( G(n,2n) \) by attaching cells of dimension \( \ge 2n+2 \): \[ \Omega \mathrm{SU} (2n) \sim G(n,2n) \cup e_{\lambda} \cup \cdots \qquad\text{with }\dim e_{\lambda} \ge 2n+2. \] It follows that \[ \pi_k (\Omega \mathrm{SU} (2n)) = \pi_k (G(n,2n)) \qquad\text{for } n\gg k. \]
It is easily shown that \[ \pi_k (\Omega \mathrm{SU} (2n)) = \pi_{k+1}(\mathrm{SU}(2n)) = \pi_{k+1}(U(2n)). \] Using the homotopy exact sequence of the fibering \[ U(n) \to U(2n)/U(n) \to G(n,2n), \] one gets \[ \pi_k (G(n,2n)) = \pi_{k-1} (U(n)). \] Putting all this together, for \( n \) large relative to \( k \), we get \[ \pi_{k-1} (U(n)) = \pi_k (G(n,2n)) = \pi_k(\Omega\mathrm{SU}(2n)) = \pi_{k+1}(U(2n)). \] Thus, the stable homotopy group of the unitary group is periodic of period 2: \[ \pi_{k-1} (U) = \pi_{k+1} (U). \]
Applying the same method to the orthogonal group and the symplectic group, Bott showed that their stable homotopy groups are periodic of period 8.
Clifford algebras
The Clifford algebra \( C_k \) is the algebra over \( \mathbb{R} \) with \( k \) generators \( e_1, \dots, e_k \) and relations \begin{align*} e_i^2 &= -1 \quad \quad \text{for } i=1,\dots, k, \cr e_ie_j &= - e_je_i \quad \quad \text{for all } i \ne j. \end{align*}
The first few Clifford algebras are easy to describe \[ C_0 = \mathbb{R},\qquad C_1 = \mathbb{C},\qquad C_2 = \mathbb{H} =\{ \text{quaternions} \}. \] If \( \mathbb{F} \) is a field, denote by \( \mathbb{F} (n) \) the algebra of all \( n{\times}n \) matrices with entries in \( \mathbb{F} \). We call \( \mathbb{F} (n) \) a full matrix algebra. It turns out that the Clifford algebras are all full matrix algebras or the direct sums of two full matrix algebras:
| \( k \) | \( C_k \) | \( k \) | \( C_k \) | \( k \) | \( C_k \) |
| 0 | \( \mathbb{R} \) | 8 | \( \mathbb{R}(16) \) | 16 | \( \mathbb{R}(2^8) \) |
| 1 | \( \mathbb{C} \) | 9 | \( \mathbb{C}(16) \) | 17 | \( \mathbb{C}(2^8) \) |
| 2 | \( \mathbb{H} \) | 10 | \( \mathbb{H}(16) \) | 18 | \( \vdots \) |
| 3 | \( \mathbb{H}\oplus\mathbb{H} \) | 11 | \( \mathbb{H}(16)\oplus\mathbb{H}(16) \) | ||
| 4 | \( \mathbb{H}(2) \) | 12 | \( \mathbb{H}(32) \) | ||
| 5 | \( \mathbb{C}(4) \) | 13 | \( \mathbb{C}(64) \) | ||
| 6 | \( \mathbb{R}(8) \) | 14 | \( \mathbb{R}(128) \) | ||
| 7 | \( \mathbb{R}(8)\oplus\mathbb{R}(8) \) | 15 | \( \mathbb{R}(128)\oplus\mathbb{R}(128) \) |
This table exhibits clearly a periodic pattern of period 8, except for the dimension increase after each period. The 8-fold periodicity of the Clifford algebras, long known to algebraists, is reminiscent of the 8-fold periodicity of the stable homotopy groups of the orthogonal group.
In the early Sixties, Michael Atiyah, Raoul Bott, and Arnold Shapiro found an explanation for this tantalizing connection. The link is provided by a class of linear differential operators called the Dirac operators. The link between differential equations and homotopy groups first came about as a result of the realization that ellipticity of a differential operator can be defined in terms of the symbol of the differential operator.
Suppose we can find \( k \) real matrices \( e_1, \dots, e_k \) of size \( n{\times}n \) satisfying \[ e_i^2 = -1, \qquad e_ie_j=-e_je_i \quad \text{for } i \ne j. \] This corresponds to a real representation of the Clifford algebra \( C_k \). The associated Dirac operator \( D=D_{k,n} \) is the linear first-order differential operator \[ D= I \frac{\partial}{\partial x_0} + e_1 \frac{\partial}{\partial x_1} + \dots + e_k \frac{\partial}{\partial x_k}, \] where \( I \) is the \( n{\times}n \) identity matrix. Such a differential operator on \( \mathbb{R}^{k+1} \) has a symbol \( \sigma^{}_D(\xi) \) obtained by replacing \( \partial/\partial{x_i} \) by a variable \( \xi_i \): \[ \sigma^{}_D(\xi) = I \xi_0 + e_1 \xi_1 + \dots + e_k \xi_k. \] The Dirac operator \( D \) is readily shown to be elliptic; this means its symbol \( \sigma^{}_D(\xi) \) is nonsingular for all \( \xi \ne 0 \) in \( \mathbb{R}^{k+1} \). Therefore, when restricted to the unit sphere in \( \mathbb{R}^{k+1} \), the symbol of the Dirac operator gives a map \[ \sigma^{}_D(\xi): \mathbb{S}^k \to \mathrm{GL} (n, \mathbb{R}). \] Since \( \mathrm{GL} (n,\mathbb{R}) \) has the homotopy type of \( O(n) \), this map given by the symbol of the Dirac operator defines an element of the homotopy group \[ \pi_k(\mathrm{GL} (n,\mathbb{R})) = \pi_k (O(n)) .\]
The paper [8] shows that the minimal-dimensional representations of the Clifford algebras give rise to Dirac operators whose symbols generate the stable homotopy groups of the orthogonal group. In this way, the 8-fold periodicity of the Clifford algebras reappears as the 8-fold periodicity of the stable homotopy groups of the orthogonal group.
The index theorem for homogeneous differential operators
The Sixties was a time of great ferment in topology, and one of its crowning glories was the Atiyah–Singer index theorem. Independently of Atiyah and Singer’s work, Bott’s paper [10] on homogeneous differential operators analyzes an interesting example where the analytical difficulties can be avoided by representation theory.
Suppose \( G \) is a compact connected Lie group and \( H \) a closed connected subgroup. As in our earlier discussion of homogeneous vector bundles, a representation \( \rho \) of \( H \) gives rise to a vector bundle \( G \times_{\rho} H \) over the homogeneous space \( X=G/H \). Now suppose \( E \) and \( F \) are two vector bundles over \( G/H \) arising from representations of \( H \). Since \( G \) acts on the left on both \( E \) and \( F \), it also acts on their spaces of sections, \( \Gamma (E) \) and \( \Gamma (F) \). We say that a differential operator \( D: \Gamma (E) \to \Gamma (F) \) is homogeneous if it commutes with the actions of \( G \) on \( \Gamma (E) \) and \( \Gamma (F) \). If \( D \) is elliptic, then its index \[ \operatorname{index} (D) = \dim \ker D - \dim \operatorname{coker} D \] is defined.
Atiyah and Singer had given a formula for the index of an elliptic operator on a manifold in terms of the topological data of the situation: the characteristic classes of \( E \), \( F \), the tangent bundle of the base manifold, and the symbol of the operator. In [10] Raoul Bott verified the Atiyah–Singer index theorem for a homogeneous operator by introducing a refined index, which is not a number, but a character of the group \( G \). The usual index may be obtained from the refined index by evaluating at the identity. A similar theorem in the infinite-dimensional case has recently been proven in the context of physics-inspired mathematics.
Nevanlinna theory and the Bott–Chern classes
Nevanlinna theory deals with the following type of questions: Let \( f:\mathbb{C} \to \mathbb{C}P^1 \) be a holomorphic map. Given \( a \) in \( \mathbb{C}P^1 \), what is the inverse image \( f^{-1}(a) \)? Since \( \mathbb{C} \) is noncompact, there may be infinitely many points in the pre-image \( f^{-1}(a) \). Sometimes \( f^{-1}(a) \) will be empty, meaning that \( f \) misses the point \( a \) in \( \mathbb{C}P^1 \).
The exponential map \( \exp : \mathbb{C}\to \mathbb{C}P^1 \) misses exactly two points, 0 and \( \infty \), in \( \mathbb{C}P^1 \). According to a classical theorem of Picard, a nonconstant holomorphic map \( f: \mathbb{C}\to \mathbb{C}P^1 \) cannot miss more than two points.
Nevanlinna theory refines Picard’s theorem in a beautiful way. To each \( a \in \mathbb{C}P^1 \), it attaches a real number \( \delta (a) \) between 0 and 1 inclusive, the deficiency index of \( a \). The deficiency index is a normalized way of counting the number of points in the inverse image. If \( f^{-1}(a) \) is empty, then the deficiency index is 1.
In this context the first main theorem of Nevanlinna theory says that a nonconstant holomorphic map \( f: \mathbb{C}\to \mathbb{C}P^1 \) has deficiency index 0 almost everywhere. The second main theorem yields the stronger inequality: \[ \sum_{a\in \mathbb{C}P^1} \delta (a) \le 2. \]
Ahlfors generalized these two theorems to holomorphic maps with values in a complex projective space \( \mathbb{C}P^n \).
In [9] Bott and Chern souped up Nevanlinna’s hard analysis to give a more conceptual proof of the first main theorem.
A by-product of Bott and Chern’s excursion in Nevanlinna theory is the notion of a refined Chern class, now called the Bott–Chern class, that has since been transformed into a powerful tool in Arakelov geometry and other aspects of modern number theory.
Briefly, the Bott–Chern classes arise as follows. On a complex manifold \( M \) the exterior derivative \( d \) decomposes into a sum \( d= \partial + \bar{\partial} \), and the smooth \( k \)-forms decompose into a direct sum of \( (p,q) \)-forms. Let \( A^{p,p} \) be the space of smooth \( (p,p) \)-forms on \( M \). Then the operator \( \partial \bar{\partial} \) makes \( \bigoplus A^{p,p} \) into a differential complex. Thus, the cohomology \( H^*\{ A^{p,p}, \partial \bar{\partial} \} \) is defined.
A Hermitian structure on a holomorphic rank-\( n \) vector bundle \( E \) on \( M \) determines a unique connection and hence a unique curvature tensor. If \( K \) and \( K^{\prime} \) are the curvature forms determined by two Hermitian structures on \( E \), and \( \varphi \) is a \( \mathrm{GL} (n,\mathbb{C}) \)-invariant polynomial on \( \mathfrak{gl} (n,\mathbb{C}) \), then it is well known that \( \varphi (K) \) and \( \varphi(K^{\prime}) \) are global closed forms on \( M \) whose difference is exact: \[ \varphi (K) - \varphi(K^{\prime}) = d \alpha \] for a differential form \( \alpha \) on \( M \). This allows one to define the characteristic classes of \( E \) as cohomology classes in \( H^*(M) \).
In the holomorphic case, \( \varphi (K) \) and \( \varphi (K^{\prime}) \) are \( (p,p) \)-forms closed under \( \partial \bar{\partial} \). Bott and Chern found that in fact, \[ \varphi (K) - \varphi(K^{\prime}) = \partial \bar{\partial} \beta \] for some \( (p-1,p-1) \)-form \( \beta \). For a holomorphic vector bundle \( E \), the Bott–Chern class of \( E \) associated to an invariant polynomial \( \varphi \) is the cohomology class of \( \varphi (E) \), not in the usual cohomology, but in the cohomology of the complex \( \{ A^{p,p}, \partial \bar{\partial} \} \).
Characteristic numbers and the Bott residue
According to the celebrated Hopf index theorem, the Euler characteristic of a smooth manifold is equal to the number of zeros of a vector field on the manifold, each counted with its index. In [13] and [12], Bott generalized the Hopf index theorem to other characteristic numbers such as the Pontryagin numbers of a real manifold and the Chern numbers of a complex manifold.
We will describe Bott’s formula only for Chern numbers. Let \( M \) be a compact complex manifold of dimension \( n \), and \( c_1(M), \dots, c_n(M) \) the Chern classes of the tangent bundle of \( M \). The Chern numbers of \( M \) are the integrals \[ \int_M \varphi (c_1(M), \dots , c_n(M)) ,\] as \( \varphi \) ranges over all weighted homogeneous polynomials of degree \( n \). Like the Hopf index theorem, Bott’s formula computes a Chern number in terms of the zeros of a vector field \( X \) on \( M \), but the vector field must be holomorphic and the counting of the zeros is a little more subtle.
For any vector field \( Y \) and any \( C^{\infty} \) function \( f \) on \( M \), the Lie derivative \( \mathcal{L}_{X} \) satisfies: \[ \mathcal{L}_{X} (fY)= (Xf)Y+f\mathcal{L}_{X} Y. \] It follows that at a zero \( p \) of \( X \), \[ (\mathcal{L}_{X} fY)_p = f(p) (\mathcal{L}_{X} Y)_p. \] Thus, at \( p \), the Lie derivative \( \mathcal{L}_{X} \) induces an endomorphism \[ L_p : T_pM \to T_p M \] of the tangent space of \( M \) at \( p \). The zero \( p \) is said to be nondegenerate if \( L_p \) is nonsingular.
For any endomorphism \( A \) of a vector space \( V \), we define the numbers \( c_i (A) \) to be the coefficients of its characteristic polynomial: \[ \det (I+tA) = \sum c_i (A)\, t^i. \]
Bott’s Chern number formula is as follows. Let \( M \) be a compact complex manifold of complex dimension \( n \) and \( X \) a holomorphic vector field having only isolated nondegenerate zeros on \( M \). For any weighted homogeneous polynomial \( \varphi (x_1, \dots, x_n) \) with \( \deg x_i = 2i \), \begin{equation} \label{characteristic} \int_M \varphi (c_1(M), \dots, c_n(M)) = \sum_p \dfrac{\varphi (c_1 (L_p), \dots, c_n(L_p))}{c_n(L_p)}, \end{equation} summed over all the zeros of the vector field. Note that by the definition of a nondegenerate zero, \( c_n(L_p) \), which is \( \det L_p \), is nonzero.
In Bott’s formula, if the polynomial \( \varphi \) does not have degree \( 2n \), then the left-hand side of \eqref{characteristic} is zero, and the formula gives an identity among the numbers \( c_i(L_p) \). For the polynomial \( \varphi (x_1, \dots, x_n) = x_n \), Bott’s formula recovers the Hopf index theorem: \[ \int_M c_n (M) = \sum_p \dfrac{c_n(L_p)}{c_n(L_p)} = \#\{\text{zeros of } X\}. \]
Bott’s formula \eqref{characteristic} is reminiscent of Cauchy’s residue formula, and so the right-hand side of \eqref{characteristic} may be viewed as a residue of \( \varphi \) at \( p \).
In [12] Bott generalized his Chern number formula \eqref{characteristic}, which assumes isolated zeros, to holomorphic vector fields with higher-dimensional zero-sets and to bundles other than the tangent bundle (a vector field is a section of the tangent bundle).
The Atiyah–Bott fixed point theorem
A continuous map of a finite polyhedron, \( f:P \to P \), has a Lefschetz number: \[ L(f) = \sum (-1)^i \operatorname{tr} f^* |_{H^i (P)}, \] where \( f^* \) is the induced homomorphism in cohomology and \( \operatorname{tr} \) denotes the trace. According to the Lefschetz fixed point theorem, if the Lefschetz number of \( f \) is not zero, then \( f \) has a fixed point.
In the smooth category, the Lefschetz fixed point theorem has a quantitative refinement. A smooth map \( f: M\to M \) from a compact manifold to itself is transversal if its graph is transversal to the diagonal \( \Delta \) in \( M \times M \). Analytically, \( f \) is transversal if and only if at each fixed point \( p \), \[ \det (1- f_{*,p}) \ne 0, \] where \( f_{*,p}: T_pM \to T_pM \) is the differential of \( f \) at \( p \).
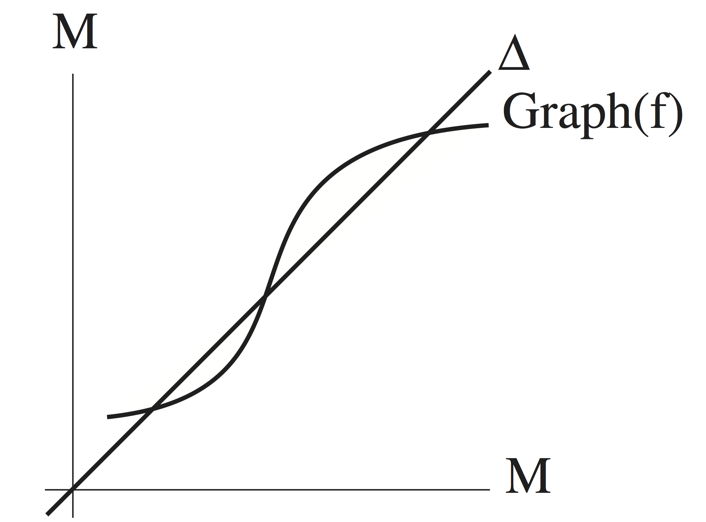
The \( C^{\infty} \) Lefschetz fixed point theorem states that the Lefschetz number of a transversal map \( f \) is the number of fixed points of \( f \), counted with multiplicity \( \pm 1 \) depending on the sign of the determinant \( \det (1- f_{*,p}) \): \[ L(f) = \sum_{f(p)=p} \pm 1. \]
In the Sixties, Atiyah and Bott proved a far-reaching generalization of the Lefschetz fixed point theorem [11], [14]. This type of result, relating a global invariant to a sum of local contributions, is a recurring theme in some of Bott’s best work.
To explain it, recall that the real singular cohomology of \( M \) is computable from the de Rham complex \[ \textstyle \Gamma \bigl(\bigwedge^0\bigr) \stackrel{d}{\longrightarrow} \Gamma \bigl(\bigwedge^1\bigr) \stackrel{d}{\longrightarrow} \Gamma \bigl(\bigwedge^2\bigr) \stackrel{d}{\longrightarrow} \cdots, \] where \( \bigwedge^q = \bigwedge^q T^*M \) is the \( q \)-th exterior power of the cotangent bundle. The de Rham complex is an example of an elliptic complex on a manifold.
Let \( E \) and \( F \) be vector bundles of ranks \( r^{}_E \) and \( r^{}_F \) respectively over \( M \). An \( \mathbb{R} \)-linear map \[ D: \Gamma (E) \to \Gamma (F) \] is a differential operator if about every point in \( M \) there is a coordinate chart \( (U, x_1, \dots, x_n) \) and trivializations for \( E \) and \( F \) relative to which \( D \) can be written in the form \[ D=\sum_{|\alpha| \le m} A^{\alpha}(x) \frac{\partial^\alpha}{\partial x^{\alpha}} \] for \( x \in U \), \( \alpha=(\alpha_1,\dots,\alpha_n) \), and \( \partial^\alpha/\partial x^{\alpha} = \partial^{\alpha_1}/\partial x_1^{\alpha_1} \cdots \partial^{\alpha_n}/\partial x_n^{\alpha_n} \), where \( |\alpha|=\sum \alpha_i \) and \( A^{\alpha}(x) \) is an \( r^{}_F{\times}r^{}_E \) matrix that depends on \( x \). The order of \( D \) is the highest \( | \alpha | \) that occurs.
Given a cotangent vector \( \xi = \sum \xi_i dx_i \in T_x^* M \), we write \[ \xi^{\alpha} = \xi_1^{\alpha_1} \cdots \xi_n^{\alpha_n} \] and define the symbol of a differential operator \( D \) of order \( m \) to be \[ \sigma (D, \xi)_x = \sum_{|\alpha| = m} A^{\alpha} (x)\, \xi^{\alpha} \,\in \operatorname{Hom} (E_x, F_x). \] In other words, the symbol of \( D \) is obtained by first discarding all but the highest-order terms of \( D \) and then replacing \( \partial^\alpha / \partial x^{\alpha} \) by \( \xi^{\alpha} \). Because \( \xi^\alpha \) transforms like \( \partial^\alpha / \partial x^\alpha \) under a change of coordinates, it is not difficult to show that the symbol is well defined, independent of the coordinate system.
Let \( E_i \) be vector bundles over a manifold \( M \). A differential complex \begin{equation} \label{complex} \mathcal{E}: 0 \to \Gamma(E_0) \stackrel{D}{\longrightarrow} \Gamma(E_1) \stackrel{D}{\longrightarrow} \Gamma(E_0) \stackrel{D}{\longrightarrow} \cdots, \qquad D^2=0, \end{equation} is elliptic if for each nonzero cotangent vector \( \xi \in T_x^*M \), the associated symbol sequence \[ 0 \to E_{0,x} \xrightarrow{\sigma(D,\xi)} E_{1,x} \xrightarrow{\sigma(D,\xi)} E_{2,x} \xrightarrow{\sigma(D,\xi)} \cdots \] is an exact sequence of vector spaces. A fundamental consequence of ellipticity is that all the cohomology spaces \( H^i = H^i(\Gamma (E_{*})) \) are finite-dimensional.
An endomorphism of the complex \eqref{complex} is a collection of linear maps \( T_i: \Gamma (E_i) \to \Gamma (E_i) \) such that \[ T_{i+1} \circ D = D \circ T_i \] for all \( i \). Such a collection \( T=\{T_i\} \) induces maps in cohomology \( T_i^*:H^i \to H^i \). The Lefschetz number of \( T \) is then defined to be \[ L(T) = \sum (-1)^i \operatorname{tr} T_i^*. \]
A map \( f: M \to M \) induces a natural map \[ \Gamma_f : \Gamma (E) \to \Gamma(f^{-1} E) \] by composition: \( \Gamma_f (s) = s \circ f \). There is no natural way to induce a map of sections: \( \Gamma (E) \to \Gamma (E) \). However, if there is a bundle map \( \varphi: f^{-1} E \to E \), then the composite \[ \Gamma (E) \stackrel{\Gamma_f}{\longrightarrow} \Gamma(f^{-1} E) \stackrel{\tilde{\varphi}}{\longrightarrow} \Gamma (E) \] is an endomorphism of \( \Gamma (E) \). Any bundle map \( \varphi : f^{-1} E \to E \) is called a lifting of \( f \) to \( E \). At each point \( x\in M \), a lifting \( \varphi \) is nothing other than a linear map \( \varphi_x: E_{f(x)} \to E_x \).
In the case of the de Rham complex, a map \( f:M\to M \) induces a linear map \[ f_x^*: T_{f(x)}^*M \to T_x^*M \] and hence a linear map \[ \textstyle\bigwedge^q f_x^* : \bigwedge^q T_{f(x)}^*M \to \bigwedge^q T_x^* M, \] which is the lifting that finally defines the pullback of differential forms \[ \textstyle f^* : \Gamma\bigl(\bigwedge^q T^* M\bigr) \to \Gamma \bigl(\bigwedge^q T^* M\bigr) . \]
Atiyah–Bott fixed point theorem: Given an elliptic complex \eqref{complex} on a compact manifold \( M \), suppose \( f: M \to M \) has a lifting \( \varphi_i : f^{-1} E_i \to E_i \) for each \( i \) such that the induced maps \( T_i: \Gamma(E_i) \to \Gamma (E_i) \) give an endomorphism of the elliptic complex. Then the Lefschetz number of \( T \) is given by \[ L(T)= \sum_{f(x)=x} \dfrac{\sum (-1)^i \operatorname{tr} \varphi_{i,x}} {|\det(1- f_{*,x})|}. \]
As evidence of its centrality, the Atiyah–Bott fixed point theorem has an astonishing range of applicability.
Here is an easily stated corollary in algebraic geometry: Any holomorphic map of a rational algebraic manifold to itself has a fixed point.
Specializing the Atiyah–Bott fixed point theorem to the de Rham complex, one recovers the classical Lefschetz fixed point theorem. When applied to other geometrically interesting elliptic complexes, Atiyah and Bott obtained new fixed point theorems, such as a holomorphic Lefschetz fixed point theorem in the complex analytic case and a signature formula in the Riemannian case. In the homogeneous case, the fixed point theorem implies the Weyl character formula.
Obstruction to integrability
A subbundle \( E \) of the tangent bundle \( TM \) of a manifold \( M \) assigns to each point \( x \) of the manifold a subspace \( E_x \) of the tangent space \( T_xM \). An integrable manifold of the subbundle \( E \) is a submanifold \( N \) of \( M \) whose tangent space \( T_xN \) at each point \( x \) in \( N \) is \( E_x \). The subbundle \( E \) is said to be integrable if for each point \( x \) in \( M \), there is an integrable manifold of \( E \) passing through \( x \).
By the Frobenius theorem, often proven in a first-year graduate course, a subbundle \( E \) of the tangent bundle \( TM \) is integrable if and only if its space of sections \( \Gamma (E) \) is closed under the Lie bracket.
The Pontryagin ring \( \operatorname{Pont}(V) \) of a vector bundle \( V \) over \( M \) is defined to be the subring of the cohomology ring \( H^*(M) \) generated by the Pontryagin classes of the bundle \( V \). In [15] Bott found an obstruction to the integrability of \( E \) in terms of the Pontryagin ring of the quotient bundle \( Q:=TM/E \). More precisely, if a subbundle \( E \) of the tangent bundle \( TM \) is integrable, then the Pontryagin ring \( \operatorname{Pont} (Q) \) vanishes in dimensions greater than twice the rank of \( Q \).
What is so striking about this theorem is not only the simplicity of the statement, but also the simplicity of its proof. It spawned tremendous developments in foliation theory in the Seventies, as recounted in [e5] and [e4].
The cohomology of the vector fields on a manifold
For a finite-dimensional Lie algebra \( L \), let \( A^q(L) \) be the space of alternating \( q \)-forms on \( L \). Taking cues from the Lie algebra of left-invariant vector fields on a Lie group, one defines the differential \[ d: A^q(L) \to A^{q+1}(L) \] by \begin{equation} \label{differential} (d\omega)(X_0, \dots, X_q) = \sum_{i < j} (-1)^{i+j} \omega\bigl([X_i, X_j], X_0, \dots, \hat{X}_i, \dots, \hat{X}_j, \dots, X_q\bigr). \end{equation} As usual, the hat over \( X_i \) means that \( X_i \) is to be omitted. This makes \( A^*(L) \) into a differential complex, whose cohomology is by definition the cohomology of the Lie algebra \( L \).
When \( L \) is the infinite-dimensional Lie algebra \( L(M) \) of vector fields on a manifold \( M \), the formula \eqref{differential} still makes sense, but the space of all alternating forms \( A^*(L(M)) \) is too large for its cohomology to be computable. Gelfand and Fuks proposed putting a topology, the \( C^{\infty} \) topology, on \( L(M) \), and computing instead the cohomology of the continuous alternating forms on \( L(M) \). The Gelfand–Fuks cohomology of \( M \) is the cohomology of the complex \( \{ A_c^*(L(M)), d\} \) of continuous forms. They hoped to find in this way new invariants of a manifold. As an example, they computed the Gelfand–Fuks cohomology of a circle.
It is not clear from the definition that the Gelfand–Fuks cohomology is a homotopy invariant. In [16] Bott and Segal proved that the Gelfand–Fuks cohomology of a manifold \( M \) is the singular cohomology of a space functorially constructed from \( M \). Haefliger [e2] and Trauber gave a very different proof of this same result. The homotopy invariance of the Gelfand–Fuks cohomology follows. At the same time it also showed that the Gelfand–Fuks cohomology produces no new invariants.
Localization in equivariant cohomology
Just as singular cohomology is a functor from the category of topological spaces to the category of rings, when a group \( G \) acts on a space \( M \) one seeks a functor that would incorporate both the topology of the space and the action of the group.
The naive construction of taking the cohomology of the quotient space \( M/G \) is unsatisfactory, because for a nonfree action the topology of the quotient can be quite bad. A solution is to find a contractible space \( EG \) on which \( G \) acts freely, for then \( EG \times M \) will have the same homotopy type as \( M \) and the group \( G \) will act freely on \( EG \times M \) via the diagonal action. It is well known that such a space is the total space of the universal \( G \)-bundle \( EG\to BG \), whose base space is the classifying space of \( G \). The homotopy theorists have defined the homotopy quotient \( M_G \) of \( M \) by \( G \) to be the quotient space \( (EG \times M)/G \), and the equivariant cohomology \( H_G^*(M) \) to be the ordinary cohomology of its homotopy quotient \( M_G \).
The equivariant cohomology of the simplest \( G \)-space, a point, is already quite interesting, for it is the ordinary cohomology of the classifying space of \( G \): \[ H_G^*(\mathrm{pt})= H^*((EG\times \mathrm{pt})/G )= H^*(EG/G)= H^*(BG). \]
Since equivariant cohomology is a functor of \( G \)-spaces, the constant map \( M \to \mathrm{pt} \) induces a homomorphism \( H_G^*(\mathrm{pt}) \to H_G^*(M) \). Thus, the equivariant cohomology \( H_G^*(M) \) has the structure of a module over \( H^*(BG) \).
Characteristic classes of vector bundles over \( M \) extend to equivariant characteristic classes of equivariant vector bundles.
When \( M \) is a manifold, there is a push-forward map \[ \pi_*^M: H_G^*(M) \to H_G^*(\mathrm{pt}) , \] akin to integration along the fiber.
Suppose a torus \( T \) acts on a compact manifold \( M \) with fixed point set \( F \), and \( \varphi \in H_T^*(M) \) is an equivariantly closed class. Let \( P \) be the connected components of \( F \) and let \( \iota_P:P\to M \) be the inclusion map, \( \nu_P \) the normal bundle of \( P \) in \( M \), and \( e(\nu_P) \) the equivariant Euler class of \( \nu_P \). In [20] Atiyah and Bott proved a localization theorem for the equivariant cohomology \( H_T^*(M) \) with real coefficients: \[ \pi_*^M \varphi = \sum_P \pi_*^P \left( \dfrac{\iota_P^* \varphi}{e(\nu_P)} \right). \] It should be noted that Berline and Vergne [e3] independently proved the same theorem at about the same time.
This localization theorem has as consequences the following results of Duistermaat and Heckman on a symplectic manifold \( (M,\omega) \) of dimension of \( 2n \):
If a torus action on \( M \) preserves the symplectic form and has a moment map \( f \), then the push-forward \( f_{*} (\omega^n) \) of the symplectic volume under the moment map is piecewise polynomial.
Under the same hypotheses, the stationary-phase approximation for the integral \[ \int_M e^{-itf} \dfrac{\omega^n}{n!} \] is exact.
In case the vector field on the manifold is generated by a circle action, the localization theorem specializes to Bott’s Chern number formulas [13] of the Sixties, thus providing an alternative explanation for the Chern number formulas.
Yang–Mills equations over Riemann surfaces
In algebraic geometry it is well known that, for any degree \( d \), the set of isomorphism classes of holomorphic line bundles of degree \( d \) over a Riemann surface \( M \) of genus \( g \) forms a smooth projective variety which is topologically a torus of dimension \( g \). This space is called the moduli space of holomorphic line bundles of degree \( d \) over \( M \).
For holomorphic vector bundles of rank \( k \ge 2 \), the situation is far more complicated. First, in order to have an algebraic structure on the moduli space, it is necessary to discard the so-called “unstable” bundles in the sense of Mumford. It is then known that for \( k \) and \( d \) relatively prime, the isomorphism classes of the remaining bundles, called “semistable bundles,” form a smooth projective variety \( N(k,d) \). In [e1] Newstead computed the Poincaré polynomial of \( N(2,1) \). Apart from this, the topology of \( N(k,d) \) remained mysterious.
In [19] Atiyah and Bott introduced the new and powerful method of equivariant Morse theory to study the topology of these moduli spaces.
Let \( P= M \times U(n) \) be the trivial principal \( U(n) \)-bundle over the Riemann surface \( M \), \( \mathcal{A}=\mathcal{A}(P) \) the affine space of connections on \( P \), and \( \mathcal{G}=\mathcal{G}(P) \) the gauge group, i.e., the group of automorphisms of \( P \) that cover the identity. Then the gauge group \( \mathcal{G} (P) \) acts on the space \( \mathcal{A} (P) \) of connections and there is a Yang–Mills functional \( L \) on \( \mathcal{A}(P) \) invariant under the action of the gauge group.
Equivariant Morse theory harks back to Bott’s extension of classical Morse theory to nondegenerate critical manifolds three decades earlier. The key result of Atiyah and Bott is that the Yang–Mills functional \( L \) is a perfect equivariant Morse function on \( \mathcal{A} (P) \). This means the equivariant Poincaré series of \( \mathcal{A} (P) \) is equal to the equivariant Morse series of \( L \): \begin{equation} \label{eqmorse} P_t^{\mathcal{G}} (\mathcal{A}(P)) = \mathcal{M}_t^{\mathcal{G}}(L). \end{equation}
Once one unravels the definition, the left-hand side of \eqref{eqmorse} is simply the Poincaré series of the classifying space of \( \mathcal{G} (P) \), which is computable from homotopy considerations. The right-hand side of \eqref{eqmorse} is the sum of contributions from all the critical sets of \( L \). By the work of Narasimhan and Seshadri, the minimum of \( L \) is precisely the moduli space \( N(k,d) \). It contributes its Poincaré polynomial to the equivariant Morse series of \( L \). By an inductive procedure, Atiyah and Bott were able to compute the contributions of all the higher critical sets. They then solved \eqref{eqmorse} for the Poincaré polynomial of \( N(k,d) \).
Witten’s rigidity theorem
Let \( E \) and \( F \) be vector bundles over a compact manifold \( M \). If a differential operator \( D: \Gamma (E) \to \Gamma (F) \) is elliptic, then \( \ker D \) and \( \operatorname{coker} D \) are finite-dimensional vector spaces and we can define the index of \( D \) to be the virtual vector space \[ \operatorname{index} D = \ker D - \operatorname{coker} D. \]
Now suppose a Lie group \( G \) acts on \( M \), and \( E \) and \( F \) are \( G \)-equivariant vector bundles over \( M \). Then \( G \) acts on \( \Gamma (E) \) by \[ (g\mathbin{.}s)(x)= g\mathbin{.}(s(g^{-1}\! \mathbin{.}x)), \] for \( g \in G \), \( s\in \Gamma(E), x\in M \). The \( G \)-action is said to preserve the differential operator \( D \) if the actions of \( G \) on \( \Gamma (E) \) and \( \Gamma (F) \) commute with \( D \). In this case, \( \ker D \) and \( \operatorname{coker} D \) are representations of \( G \), and so \( \operatorname{index} D \) is a virtual representation of \( G \). We say that the operator \( D \) is rigid if its index is a multiple of the trivial representation of dimension 1. The rigidity of \( D \) means that any nontrivial irreducible representation of \( G \) in \( \ker D \) occurs in \( \operatorname{coker} D \) with the same multiplicity and vice versa.
If the multiple \( m \) is positive, then \( m\mathbin{.}1= 1\oplus \dots \oplus 1 \) is the trivial representation of dimension of \( m \). If \( m \) is negative, the \( m\mathbin{.}1 \) is a virtual representation, and the rigidity of \( D \) implies that the trivial representation 1 occurs more often in \( \operatorname{coker} D \) than in \( \ker D \).
For a circle action on a compact oriented Riemannian manifold, it is well known that the Hodge operator \( d+d*: \Omega^{\text{even}} \to \Omega^{\text{odd}} \) and the signature operator \( d_s=d+d^*:\Omega^+ \to \Omega^- \) are both rigid.
An oriented Riemannian manifold of dimension \( n \) has an atlas whose transition functions take values in \( \mathrm{SO} (n) \). The manifold is called a spin manifold if it is possible to lift the transition functions to the double cover \( \mathrm{Spin} (n) \) of \( \mathrm{SO} (n) \).
Inspired by physics, Witten discovered infinitely many rigid elliptic operators on a compact spin manifold with a circle action. They are typically of the form \( d_s \otimes R \), where \( d_s \) is the signature operator and \( R \) is some combination of the exterior and the symmetric powers of the tangent bundle. In [21] Bott and Taubes found a proof, more accessible to mathematicians, of Witten’s results, by recasting the rigidity theorem as a consequence of the Atiyah–Bott fixed point theorem.
The idea of [21] is as follows. To decompose a representation, one needs to know only its trace, since the trace determines the representation. By assumption, the action of \( G \) on the elliptic complex \( D: \Gamma (E) \to \Gamma (F) \) commutes with \( D \). This means each element \( g \) in \( G \) is an endomorphism of the elliptic complex. It therefore induces an endomorphism \( g^* \) in the cohomology of the complex. But \( H^0 = \ker D \) and \( H^1=\operatorname{coker} D \). The alternating sum of the trace of \( g^* \) in cohomology is precisely the left-hand side of the Atiyah–Bott fixed point theorem. It then stands to reason that the fixed point theorem could be used to decompose the index of \( D \) into irreducible representations.