by Loring W. Tu
Loring W. Tu coauthored Differential Forms in Algebraic Topology with Raoul Bott. A second volume, Elements of Equivariant Cohomology, in the works long before Bott’s passing, is due to appear in 2014.1
Making a problem your own

The first time I met Raoul was at an orientation lunch for incoming graduate students in mathematics at the Harvard Faculty Club. Raoul gave us some advice on how to write a Ph.D. thesis. He said it was like doing a homework problem, but a harder problem. He ended by saying, “Make the problem your own.” It puzzled me what it meant to “make a problem my own,” but I was too intimidated to ask. I thought it was one of those things, like the taste of a certain fruit, that is impossible to explain except to those who have experienced it themselves.
A few years later, when I was an assistant professor at the University of Michigan, my Ph.D. thesis advisor, Phil Griffiths, came to visit. I picked him up from the airport and drove him to a restaurant. While in the car, we started talking about a mathematical problem. I became so engrossed that I lost all sense of time, place, and orientation. The next thing I knew, a policeman was handing me a ticket for driving the wrong way on a one-way street.
Griffiths advised me helpfully, “Go tell the judge that you were thinking about mathematics.” So I showed up in court to dispute the charge, and I did as Griffiths told me. The judge took a look at my driver’s license and said, “You live only one block away from this street. You have no excuse!” He upheld the fine of seventy-five dollars. At that moment, it dawned on me what Raoul had meant by “making a problem your own.” I think it meant to be so absorbed by the problem that you forget everything else — to be possessed, so to speak.
It has happened to me a few more times, missing a subway stop on my way to the airport or jumping out of bed at night with a solution. Each time I feel that I have finally made a mathematical problem my own.
Bott as a lecturer

Bott’s lectures were legendary. He had a knack for explaining ideas in simple, easily understood terms, no matter how abstruse, complicated, or abstract the topic. His lectures were always clear and exciting. They were magical in that they gave you the feeling you had understood something, sometimes even when you had not. Not surprisingly, his lectures were popular and his courses heavily enrolled. His courses had impact beyond mathematics students at Harvard, for they were attended also by students and faculty from other departments and other universities. The physicist Cumrun Vafa cited Bott’s courses for changing his perception of modern mathematics and profoundly influencing his later studies ([e5], p. 277). Likewise, Edward Witten credited Bott’s lectures with teaching him techniques of geometry and topology, such as Morse theory and equivariant cohomology, which have proven pivotal in his work on supersymmetry.
Bott always seemed glad to be in the classroom. His courses were a lot of fun. In every lecture there were spontaneous moments of laughter. This came about not through preparation and canned jokes but because of his innate sense of humor, unique perspective, colorful phrases, and superb delivery. In his hands, the construction of a spectral sequence could become entertaining. He always focused on the central idea and simple but illuminating examples.
Authority
One year Bott taught the second semester of complex analysis, and the textbook he chose was Lars Ahlfors’s Complex Analysis. At some point he departed from the book and gave a different definition. Now students often revere the textbook as the ultimate authority, so a hand shot up and a student blurted out, “But Ahlfors says this, not that!” Bott replied calmly, “Yes, but Bott says that.” As usual, Bott understood things his own way and was not about to faithfully follow any book. In fact, in topology courses he did not even follow his own books, because usually his understanding of the subject had evolved since the book appeared.
A conscripted lecture
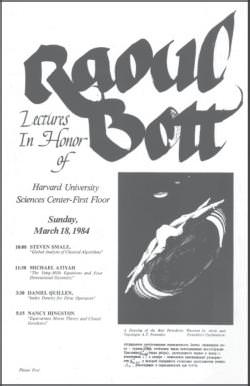
One day in the early 1980s a poster appeared on the bulletin board of the Harvard mathematics department on the third floor of the Science Center. It looked just like any other announcement, but with a twist. On the top it said, “By popular demand, Professor Raoul Bott will give a lecture on ‘The Atiyah–Singer Index Theorem: What It Really Means’ ”. The date, time, and place of the lecture were all clearly spelled out. What was unusual about this poster was the presence of an asterisk next to Raoul Bott’s name and a footnote at the bottom: “*Please inform the speaker.”
A few minutes before the scheduled time on the appointed day, the room was packed. No one had the temerity to inform the speaker about the lecture, so we were all wondering if Raoul Bott was going to show up. At the appointed time, he showed up, made a few jokes, and then proceeded to deliver a wonderful lecture on the Atiyah–Bott fixed point theorem and the Atiyah–Singer index theorem, all in the allotted hour.
Finder’s fee
Nowhere were Bott’s powers of persuasion more evident than at the seventy-fifth anniversary of the Institute for Advanced Study at Princeton in March 2005. On that occasion he gave a talk reminiscing about how the institute in the fifties changed his life and launched his career (Figure 38). A few days after the conference, Bob MacPherson, a professor at the institute, called him to say that a couple in the audience that day were so moved by Bott’s talk that they donated two million dollars to the institute. Bott recounted the story to me and added, “I should have asked for a finder’s fee.”
Liquors

Coming from a family of teetotalers, I knew nothing about alcohol as a graduate student. At one point I thought it would be good to repair my ignorance in this domain. Raoul had the look of a bon vivant who might be knowledgeable about such things. Just as some students might ask him for good references in topology, when I ran into him in the elevator one day I asked him, “Professor Bott, can you recommend some liquors to me?” He gave me a sly look sideways, and said, “Candy is dandy, but liquor is quicker!” before mentioning a few brands. To this day I remember the aphorism but not the brands of liquor he recommended.
Joint books
When I first started working on the book Differential Forms in Algebraic Topology with Raoul, I was a graduate student. He thought that we made a great pair working together, because as a graduate student I would know first-hand the difficulties a student would encounter in learning the subject. I think Raoul did not anticipate that it would end up taking up so much of my time. In the end I was glad to have written the book with him. For me it was a form of apprenticeship, and I felt that I had learned a tremendous amount of mathematics from a master.
Raoul was pleased with the resulting book. Once in a lecture I attended, he mentioned some facts — I forget about what, maybe de Rham cohomology or spectral sequences — and told the audience that they could find them all in the “Bible”. There was a momentary perplexity among the audience, and then it transpired that Bott was referring to our joint book. For a devout Catholic like Bott to compare our book to the Bible must have been the highest form of compliment.

Although we had projected a second volume, Raoul did not mention it after the completion of the first, possibly because he did not want to put me through the experience again. It was many years later that I brought it up. The book would be called Elements of Equivariant Cohomology. We worked on it for many years. My chief regret is that we did not finish it while he was alive, but I have hope that it will soon see the light of day.
While working on the books, Raoul often told me to be “generous with credit to others.” Human nature being what it is, we probably all have the tendency to overestimate our own contribution and, conversely, to underestimate that of others. These days, whenever my baser nature threatens to come to the fore, I remember this lesson from Raoul.
One reason we got along so well I think is that with my strict Confucian upbringing, in which every edict is serious, I found Raoul’s wit and irreverence refreshing. As for Raoul, he said that as he got older, he liked more and more the Confucian reverence for the aged.
Personal happiness

Raoul had a playful streak that persisted throughout his life. He liked to tease everyone: his wife, children, friends, colleagues, and even students. His interaction with me was no exception.
His concern for me extended to my personal happiness. My time as a graduate student at Harvard overlapped with that of Nancy Hingston, a good friend of mine and a student of his of whom he thought highly. I remember at a conference, Raoul once put his arm around her shoulder and exclaimed to the public, “My finest student!” On the day that Nancy got married, Raoul said to me, “Loring, you missed your chance.”
Dust bunnies

In my first year as an assistant professor at Michigan, I worked long distance with Raoul on the book Differential Forms in Algebraic Topology. That summer I returned to Harvard to facilitate our collaboration. At the time Raoul and his wife, Phyllis, were comasters of Dunster House, a Harvard undergraduate house with three hundred undergraduates. Too cheap to rent a place of my own, I asked Raoul if he had a guestroom for me in the Dunster House master’s residence. Bott readily agreed.
The guestroom was a room attached to the master’s residence but with a separate entrance. This way I had my privacy, but I could go into the master’s residence to use the kitchen and dining room. To afford Raoul and Phyllis their privacy, I normally did not do that except when they were away. The Botts by then had a house on Martha’s Vineyard and would often spend a large part of the summer there. I worked with Raoul on occasional trips to the Vineyard or when he returned to Cambridge from time to time.
As comasters of Dunster House, Raoul and Phyllis often had to entertain on a large scale, holding receptions for students and parents, for example, and so Harvard provided them with live-in help, who were usually graduate students in fields other than mathematics. The live-in help lived upstairs from the Botts, so that summer I found myself living in the Dunster House master’s residence with three young women, the live-in help of the year.
The first time Raoul came back in the summer, he got very mad at the four of us; apparently we had been living in squalor (though not in sin). Pointing to dust bunnies everywhere, he said, “Look at this!” The three young women were not used to cleaning the house, because during the school year there was a cleaning staff from Harvard. As for me, at that point of my life I was oblivious to dust bunnies; they were simply invisible to me. It was strange that as in mathematics, where, after Raoul showed me his fixed-point theorems, I began to see fixed-point phenomena everywhere, in the same way, after Raoul pointed out those dust bunnies, I began to notice dust bunnies everywhere. After that, each time just before Raoul was to return to Cambridge, my three housemates and I would clean the master’s residence from top to bottom.
Book contract

The dust-ball incident was one of only two times that I saw Raoul get mad. The other time had to do with the contract for our book. While working on the book, we circulated the manuscript to some colleagues and students for feedback. Possibly because of Raoul’s fame, the book was heavily courted by publishers. Both Walter Kaufmann-Bühler, the mathematics editor at Springer, and Klaus Peters, the editor at Birkhäuser, at the time an independent publisher,2 came to Harvard to lobby us for their book series. We chose Springer, not only because of its long history and excellent reputation for quality but in part because of the better royalty Springer offered.
After the book was published, Kaufmann-Bühler was quite happy, because as he told me, “The book was selling like hotcakes.” He passed away a few years later and was replaced by a succession of editors at Springer. At one point, one of the new editors sent me a letter, pleading difficult financial circumstances at Springer and asking Raoul and me to sign a new contract with a lower royalty rate.
For Raoul, I think the royalty was not an issue at all, but for me, a low-paid assistant professor at the time, it was much more significant. With the letter in hand, I walked into Raoul’s office, looking frantic. When Raoul saw me and read the letter, he got quite mad. He said, “They signed a contract. Tough luck.” He then picked up the phone and called the editor. In his usual authoritative voice, he told the editor firmly that we had no intention of renegotiating the contract. That was the end of it. Springer backed off and seems to have flourished.
Style
At a conference in Montreal in 2008, Michael Atiyah said that someday historians of mathematics may want to decipher joint papers to figure out who wrote what. In some cases this may be quite easy. Raoul was a consummate stylist. His writings were pithy. He had a colorful, inimitable way of expressing himself. People have often come up to me to tell me how much they like our book. Sometimes, as if to prove that they have read it, they cite specific passages that they like best. Much to my chagrin, these are usually not the ones I wrote.
Sleeping in another woman’s bed

Jane Kister was a young logician at the University of Oxford in the seventies. In the fall of 1978, just after marrying the topologist Jim Kister, Jane spent a sabbatical semester at MIT. At a reception at Harvard, Raoul put his arm around her and announced, “I’ve slept in this woman’s bed.” Jane’s face turned beet red. What happened was that Jane was also on sabbatical in the spring of 1977 and had rented her house in Oxford to the Botts. It was indeed true that Raoul had slept in Jane’s bed, though not simultaneously with her.
While visiting England in the early eighties, Raoul thought that he had also slept in Queen Elizabeth’s bed, but of course without the queen in it. In his Collected Papers he credited this experience with his sudden joint insight with Michael Atiyah into the relation between equivariant cohomology and the moment map ([4], p. xiii): “Possibly the night I had spent in the erstwhile bed of Queen Elizabeth had something to do with it!” According to a recent message from Atiyah, the queen was Victoria, not Elizabeth. Raoul had stayed with the Atiyahs in the Master’s Lodge at Trinity College, Cambridge, where Atiyah was then the master. In her time, Queen Victoria and her consort, Prince Albert, did in fact stay as guests at Trinity College, and the four-poster bed that they used became a guest bed.
Lecture preparation
One year when I was at the University of Michigan, Raoul was invited to give a lecture in a prestigious series. During his visit to Ann Arbor, Raoul stayed with me in my one-bedroom apartment. The morning of the lecture, he was writing his lecture notes. After writing seven pages, he said, “That’s enough. I will not be able to cover more than five pages in an hour.” I have found this to be a useful rule of thumb: five to seven pages of handwritten notes are about right for an hour lecture on the blackboard. I learned more from Raoul’s leisurely but well-timed pace of five handwritten pages in an hour than from other people’s fifty slides, each densely packed with information.
Another narrow escape

Raoul’s life seemed to be blessed. He left his native Hungary/Slovakia before the Nazi invasion, survived near-drowning in an expedition organized by Stephen Smale, and visited India without a visa at a time when visas were required. In Ann Arbor he also had a narrow escape.
At the end of his visit to Ann Arbor, I drove him to the Detroit International Airport, twenty miles away, in my Ford Maverick. It was a used car that I had bought from a departing postdoc at the University of Michigan. Soon after I purchased the car, I noticed that it was leaking transmission fluid, but the rate of the leak was so slow — just one or two drops a day — that it did not seem worthwhile to replace the entire transmission. On the highway as we were heading towards the airport, the car started smoking under the hood. We were alarmed, but Raoul had a plane to catch and the airport was not so far away, so I continued driving at full speed.
Just as we arrived at the airport, dense white smoke billowed from under the hood and the car went dead. It looked like it could explode. Raoul hurriedly ran to his flight, and I jumped out of the car. After his return to Boston he called me to make sure that I was still alive.
The Toaster Incident at Dunster House

Raoul navigated the perils of academic politics with consummate skill. He and Phyllis were comasters of Dunster House for six years. After they stepped down, another professor was appointed as the master. To distinguish him from Raoul, I will call him the new master. The new master was a very nice man, but his term was marked by controversy. I will give one example. It stemmed from a toaster oven.
Some Jewish students did not want to eat the food in the dining hall for reasons of keeping kosher. They asked the new master for a toaster oven so that they could heat up their own kosher food. The new master bought a toaster oven for them. One of the tutors (academic advisors) at Dunster House, an activist with strong principles, wrote a letter to the student paper, the Harvard Crimson, criticizing the use of house funds to buy the toaster oven, because in his view this was an act of favoritism towards one particular religion, akin to a violation of the separation of church and state, a founding principle of our republic.
The new master fired this tutor. More letters followed in the Crimson. It was no longer about the toaster oven, but about the new master’s leadership. Other tutors wrote letters, accusing the master of autocracy and partiality, of favoring some tutors over others. There were calls for the master’s ouster. Students organized demonstrations in Harvard Yard supporting the fired tutor. Professor Edmund Lin, a former chair of the Department of Molecular Genetics at Harvard Medical School and a member of the Senior Common Room of Dunster House, wrote a letter to President Rudenstein of Harvard, calling for the master’s resignation. Only at Harvard could there be a raging debate about constitutional principles arising from a toaster oven. This was when the new master’s five-year term was up for renewal. President Rudenstein asked to meet with Raoul, evidently because he valued Raoul’s judgment. Knowing that I was a close friend of Edmund Lin, Raoul asked me if I knew what was going on. I did, not only because of my friendship with Edmund Lin but also because I read the Crimson every day. Raoul did not read the Crimson.

When I explained the incident to Raoul, his immediate reaction was “An activist troublemaker? You should never fire someone like that. If you do, there is no end to the trouble. You should give him tenure!” Raoul had a very good nose for staying out of trouble. Of course, this did not mean that he would give every activist tenure. It just meant that in this case the stakes were not high enough to fire the tutor. Raoul then said pensively, “Ed Lin was always so quiet when I was the master. He must have thought that I was doing a good job.”
It so happened that the new master was an ethnic Chinese from Indonesia, a resident tutor whom he particularly liked and was accused of being partial to was a Chinese-American, and the professor calling for the master’s ouster was a Chinese from China. Raoul turned to me and asked, “Is this one of those Chinese battles so inscrutable to us Westerners?”
I do not know what he said to President Rudenstein. Rudenstein renewed the contract of the new master. The controversy died down after the students graduated. Edmund Lin told me afterwards, “I am sure it was Raoul who saved the new master’s skin.”
Foreign languages
Raoul had a wonderful self-deprecating sense of humor. He was a talented linguist. He spoke German, Hungarian, and Slovak fluently, not to mention English, of which he was a master. But there is a limit to the number of languages one can learn or need to learn. I like his experience with Italian. Before a conference in Italy, he bought a cassette course on Italian. Repeating the sentences on the cassette tape, he studied Italian for two weeks. When he got to Italy, he found that he had forgotten all the sentences except for one. He told me that the one sentence he could say in Italian was “Ascolti e ripeta,” which means “Listen and repeat.”
Nonmathematical activities

In spite of his prodigious output in mathematics, Raoul found time to do other things. As comasters of Dunster House, Raoul and Phyllis actively participated in the life of the undergraduates, sharing meals with them, meeting with their parents, and organizing and attending cultural activities in the house. Raoul played the piano well enough to give public performances. Ever the good sport, he took part in an undergraduate theater production, playing a Hungarian linguist in My Fair Lady. At one Halloween party, Raoul and Phyllis dressed up as a pirate king and a young maiden, but two students upstaged them by dressing up as Raoul and Phyllis Bott! The male student sported a big beard and was chock-full of gray hair, and to top it off, he was carrying Raoul’s signature briefcase (Figure 33).
An avid swimmer and a regular on the clothing-optional beach of Martha’s Vineyard, Raoul earned himself the sobriquet “The Mayor of Lucy Vincent Beach”. He played tennis and bicycled to work. Once when I visited his home, he showed me with great pride some kitchen renovation, saying that he did it all with a router.
Material enjoyment

From Raoul, I learned that a lifelong dedication to intellectual pursuits is not incompatible with enjoyment of material things.
Raoul bought a beautiful house on Martha’s Vineyard. Although the house was not right on the water, it was surrounded by an expanse of wild vegetation and had an unobstructed view of the ocean. There was even a brook on the property. Since most of the houses there were hidden in dense foliage, Raoul’s house had a view of nature with no other sign of human habitation. One day another house rose up, towering above the canopy of trees in full view from Raoul’s window, the only house visible in otherwise pristine nature. Raoul said it stuck out like a sore thumb, but he was philosophical about it. After all, his own house might be a sore thumb to the other owner.
While we were working on the book Differential Forms in Algebraic Topology, he teased me about the enormous amount of time I was spending on it, asking me if I thought that with the expected royalty it would come out to minimum wage. Then he said, “I want to buy a boat with it.” I thought he was joking, but years later he did buy a boat.
Raoul had a fascination with cars, and on one visit he proudly showed me his collection, a single 2-inch exact replica of a Jaguar that he said a student of his gave him. Finally, at the age of seventy-four, he bought a BMW, exemplifying another piece of advice he gave me: “Live it up!”
Mineral collection
One of the pleasures of talking to Raoul was the unexpected insight that he often offered. Sometime in the early nineties, Raoul received in the mail a calendar of Steve and Clara Smale’s priceless collection of natural crystals, lovingly and beautifully photographed by Steve Smale himself. Raoul showed me the calendar in his office, and while admiring the breathtaking beauty of the minerals, he said, “What a way to avoid inheritance tax! You just have to slip a few of these to your children.” Of course, he did not mean it as an estate-planning tip; besides, I had neither a fortune nor children to benefit from this advice, but it was so characteristic of Raoul to have a unique perspective on everything.
Practical advice

Fresh out of graduate school, I once visited Raoul on Martha’s Vineyard to work on our joint book. Sitting on a bench surveying his beautiful estate, he said to me, “Loring, buy land.” At the time I was too poor to buy anything, but time has borne out the wisdom of his advice, especially when the land is in a well-chosen location like Martha’s Vineyard.
One of Raoul’s observations on life has played a crucial role in my mental equilibrium. When he was at the Institute for Advanced Study at Princeton in 1949–51, he once had a conversation with John von Neumann, a fellow Hungarian who was at the time a professor at the institute. Von Neumann told Raoul that he had known only one great mathematician, David Hilbert, and that having been a prodigy in his youth, he never felt that he had lived up to his promise. Raoul wrote in ([4], p. 270), “So you see, it is not difficult to be found wanting — one just needs an appropriate measuring rod.” If even von Neumann felt inadequate in his achievement in comparison with Hilbert’s, what chance for professional satisfaction do we ordinary mortals have? After Raoul recounted this incident to me, I resolved never to compare myself with anyone else, especially not with my friends and classmates who have achieved greatness.
I was fortunate to be in the job market during a brief window of opportunity when there were many jobs available, and so I actually had a few choices. Tufts had a fine reputation and excellent colleagues, but what clinched the deal was what Raoul said to me, “It will be nice to have you in the backyard.” The physical proximity made collaboration easier, and after moving to Tufts, I worked on a few more joint projects with him and had the pleasure of attending more of his courses.
Favorite theorems

After the memorial service for Raoul in January 2006, Michael Atiyah gave a compelling lecture on why the Atiyah–Bott fixed point theorem should have been one of Raoul’s top five favorite theorems. I think Raoul would have agreed. The list of five was a rather artificial framework and should probably not be taken too literally. It was what came to Raoul’s mind on the spur of the moment, but he simply could not fit all of his favorite theorems in there. In the end, my article included another thirteen in addition to the top-five list.
The Wolf Prize

Raoul used to say that there were two kinds of mathematicians, smart ones and dumb ones. The smart ones were people like Michael Atiyah and Jean-Pierre Serre, who understood new ideas quickly. He classified himself as a dumb mathematician, because understanding came to him slowly. This may be so, but his understanding was profound, as his corpus of many beautiful and deep theorems attests. If he did not understand something, he had no hesitation in saying so. When he was awarded the Wolf Prize, he told me that he was in very good company, because he was sharing the prize with Serre.
One of them had to give a speech in the Knesset, the Israeli parliament. According to Raoul, Serre wanted him to give the speech, because Serre thought that Raoul “had a better stage presence” and that Raoul “looked more like a mathematician.” But how to explain to the Israeli lawmakers the research for which they were being awarded the prize? This is the usual conundrum of pure mathematicians called upon to explain their work. Serre came up with a gem that Bott incorporated into his speech:
Mr. President of the State, Mr. Speaker of the Knesset, Mr. Minister of Education, Members of the Diplomatic Corps, Dear Colleagues and Guests:
It is a great honor for me to rise in this beautiful chamber and in so distinguished a company to accept the Wolf Prize in Mathematics on behalf of Jean-Pierre Serre and myself.
Thank you.
In our field alone the previous winners of this Prize include both heroes of our youth and cherished friends. And if we look beyond, well, who would not be delighted — as well as humbled — to join a list that, so to speak, starts with Marc Chagall!
My first words of thanks here are in tribute to Ricardo and Francisca Wolf for setting up a foundation so much in tune with the most essential need of our ever-shrinking planet. The universality of their purpose speaks for itself:
“To promote science and art for the benefit of mankind.”
And how inspired of them to see the commonality of art and science, and to include mathematics, where these two spheres of endeavor are well nigh indistinguishable, in their generous bequest.
But we feel doubly honored that a small and relatively new country, with so many pressing and highly nontrivial — as we say in our mathematical jargon — problems on its agenda, nevertheless finds time to bestow this award at its highest level. This act alone is a moving tribute to the life of the spirit in a world mostly concerned with more mundane things.
Unfortunately, the very term “Mathematics” strikes terror in most mortal hearts, and so it is possibly appropriate here to put our subject into some sort of perspective. And I can think of no better way of doing this than to divulge to you just how my junior, but much wiser, colleague Jean-Pierre Serre cajoled me into being the one to deliver this acceptance speech. “For if I were to give the speech,” he argued, “then all I would say is that while the other sciences search for the rules that God has chosen for this Universe, we mathematicians search for the rules that even God has to obey.” And I certainly couldn’t let him get away with that!
But, after this little tongue in cheek, my time is definitely up!
Still, please permit me two more words of thanks. The first is to the committee that had a long enough memory to settle on us from amongst so large an array of worthy and younger candidates. And our final thank you is to our families and especially our wives, who for a lifetime have put up with our absent-minded ways and have been our anchors in the real world.
Final years

Soon after their move, Raoul was diagnosed with lung cancer. In spite of the poor prognosis, he was his usual cheerful self. He explained the principle of chemotherapy to me this way: “It tries to kill the cancer faster than it kills you.” He faced the prospect of death with equanimity. When I asked him if he would be returning to Massachusetts at some point, he pointed to the ground and said, “I am going in here.”3

It has often been said that mathematics is a young person’s game. Raoul’s life is a particularly inspiring counterexample. I saw him three weeks before he passed away. I had been working on a problem with him on the volume of a symplectic quotient. He was in top form mentally. He explained to me a new way of looking at the problem that greatly simplified it. I cried, “This is so simple!” He said, “That’s the way I like it.”
At the age of eighty-two, battling cancer, he was still trying to understand integration on a symplectic quotient. There was a paper of Victor Guillemin and Jaap Kalkman on the subject, but he wanted to understand it in his own way. Clearly, his motivation was not any external reward, like an NSF grant or more honors. He simply wanted to understand. He was a true mathematician.
His life showed us what is humanly possible. He continued to make beautiful discoveries and publish important papers to the very end.
Royal Society

In the final year of his life, Bott was inducted into the Royal Society. The Royal Society dates back to 1660 and is a roster of luminaries in the history of science. Each new fellow signs in a book that has the signatures of all former and current fellows. For health reasons, Bott was not able to travel to London for the signing, but Michael Atiyah, a former president of the Royal Society, brought to California the actual page from the book Bott was to sign. For good measure, Atiyah also brought Raoul a scanned and bound copy of the preceding pages. An induction ceremony was held at the Kavli Institute for Theoretical Physics, University of California, Santa Barbara, in October 2005.
When I visited Raoul in California a month later, he excitedly showed me pages from his copy of the Royal Society book, exclaiming, “Look at this! Christopher Wren! Isaac Newton! George Stokes! Lord Kelvin!” For a man of science, this may be the ultimate good company.