| [handwriting] March 26, 2002 |
Dear Yves,
I’d just been typing a long email to you for over an hour when Netscape gave up the ghost and the whole message was lost. You might say there’s some divine justice there — that this is my punishment for not having replied to you sooner. So here I am writing by hand (at least you’ll have the accents which I still haven’t figured out how to make on this keyboard that lacks them), and I’m enclosing photocophies of the articles I’m discussing.
Again, sorry I didn’t reply sooner to your emails. You’re right; it’s a chore that’s being asked of you, and I should have worked to lighten your task right away. But I had no way to know: I wasn’t aware that Björn [Engquist] had put you on the list of names suggested to the Dean. (But that’s not really a good excuse: Björn had asked me for 5 or 6 names, and I gave him 2 right away, saying that I’d email the others — but then I forgot.) I’ve also wondered why you might be unable to view a Lucent web page: maybe it’s because viewing from outside the US is blocked? In any case, here is the web address that works for me:
http://wim.sweldens.com
\begin{array}{c}\hline\qquad\qquad\qquad\end{array} (Continuation 2 days later, after my phone call of March 27.) I will fax this letter to you, as agreed, and I’ll also send it in hard copy, together with the articles that I discuss in the letter.
The Dean, and through him, the Committee on Appointments and Tenure, don’t expect from you an in-depth analysis of all aspects of his work. In fact they have chosen (or Engquist and Dobkin have chosen for them) experts in the various fields. So if you wish you can say from the get-go that you will be discussing only certain aspects of his scientific output, leaving the rest to other experts.
From the viewpoint of Applied Math at Princeton, we have been searching for years for someone who would interest both the Dept. of Computer Science and us, but there clearly has been a mismatch. The people I put forth when I was the director, such as Rokhlin, Engquist, Bill Cook and even Adelman, from MIT, did not interest them at all, or only mildly; they were warmer on Greengard (who however did not want to leave NYU), but their counterproposals were mainly people who we regarded as much less strong, such as Eric Gross [sic], or who were working in less interesting areas (like Demmel — heavy-duty linear algebra software). Regarding Wim Sweldens, on the other hand, there is interest on both sides: the computer graphicists are very impressed by his SIGGRAPH track record, that being a conference that has as many participants (about 4,000) and as much prestige in computer graphics as the ICM in mathematics. In general, a talk at ICM is easily enough, without further ado, to secure a tenured position in a top department in this field. At the same time, there is also interest in him among our group, not only on my part (or I would never have proposed him), but also on the part of Björn Engquist and Weinan E, who have had very productive conversations with him.
\begin{array}{c}\hline\qquad\qquad\qquad\end{array}
What I find most interesting in Wim, and what is for me the main reason why he’s attractive as a bridge between applied math and computer sciences, is that he has a very good grasp of mathematical intuition, and is interested not only in getting software and programs to work well, but also in studying the mathematical reasons for their success (like me, he believes that good software requires not only good “cooking skills” — though that plays a role too — , but also, and primarily, essentially mathematical ideas. For example: integration by Lebesgue’s method yields an algorithm that is far better than Riemann’s.) Therefore he’s always interested in exploring the mathematical aspects of certain developments, even if that requires (on a first approach) a drastic simplification in the description, beyond what other computer scientists would consider reasonable. And in our collaboration, he often has his share of key ideas, even though more often than not the technical component falls to me.
\begin{array}{c}\hline\qquad\qquad\qquad\end{array}
I’m enclosing here his list of publications. I’ve marked a few which I will describe below. I will include copies of them in the packet that I’ll send you. These articles illustrate three “themes” in my “Sweldens file” for your benefit, all within the framework of the interaction “applied math \( \leftrightarrow \) algorithms”.
\begin{array}{c}\hline\qquad\qquad\qquad\end{array}
I. Lifting
“Lifting” is Sweldens’ name for a construction that allows the construction of longer wavelet filters starting from shorter ones. It its most primitive form, it amounts to a simple algebraic observation: \begin{equation}\label{eqon} \eqalign{ \text{if }\quad & m_0 (\xi)\quad \text{ and } \quad \tilde{m}_0(\xi) \text{ satisfy }\cr & m_0 (\xi) \, \overline{\tilde{m}_0 (\xi)} + m_0(\xi + \pi)\, \overline{\tilde{m}_0 (\xi+\pi)} =1, \tag{*} } \end{equation} and if we define \[ m^{\#}_0 (\xi)=\tilde{m}_0(\xi) + e^{-i\xi} \alpha (2\xi)\, \overline{m_0\,(\xi+\pi)}, \] where \( \alpha \) is any trigonometric polynomial, then the pair \( m_0,m^\#_0 \) also satisfies \eqref{eqon}. Several people have made this observation independently: Sweldens, Dahmen & Micchelli, Herley & Vetterli — and all in all, it’s a fairly trivial one. They all observed as well that biorthogonal wavelet splines can be generated from the trivial pair \( m_0 = \frac{1}{\sqrt{2}} \), \( \tilde{m}_0 = \frac{1}{\sqrt{2}} \) in two steps: \( m,\tilde{m}_0 \rightarrow m_0, m^{\#}_0\rightarrow m^b_0, m^{\#}_0 \) (dual operation). The difference between Sweldens’ work and the others’ is the interpretation he gave (in terms of prediction and updating — see article A), which then allows several very useful generalizations and applications:
• “in-place” algorithm: for instance, in Haar:
standard alg.:
\[
\eqalign{
c^0_k \longrightarrow s^1_k &= \frac{c^0_{2k} + c^0_{2k+1}}{2}\cr
d^1_k &= c^0_{2k+1} - c^0_{2k}}\quad
\text{(non-normalized).}
\]
One must store the \( c^0_{2k} \), \( c^0_{2k+1} \) in memory after
calculating the \( s^1_k \), in order to calculate the \( d^1_k \).
lifting alg.:
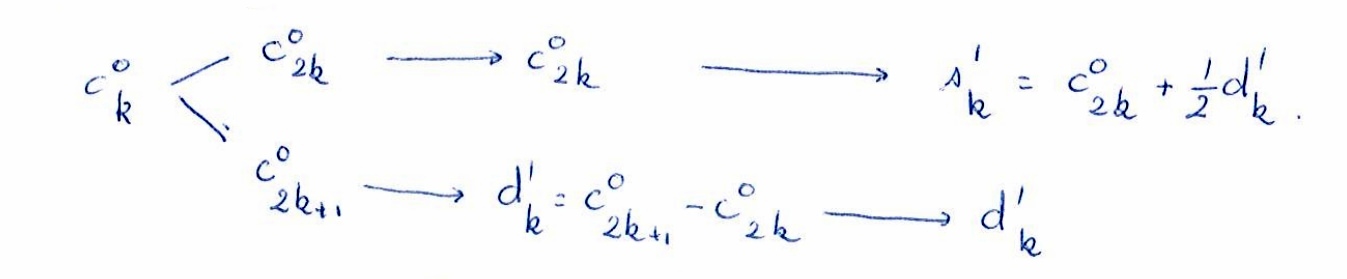
For each calculation: one quantity is replaced by another (\( c^0_{2k+1} \) by \( d^1_k \), later \( s^1_k \) by \( c^0_{2k} \)).
This allows one to make much bigger calculations and in situations where the “prediction” and the “update” are not uniform, as in the
• application to nonuniform surfaces and triangulations (see article A: second-generation wavelets)
• in the setting of the 2 triangular operations
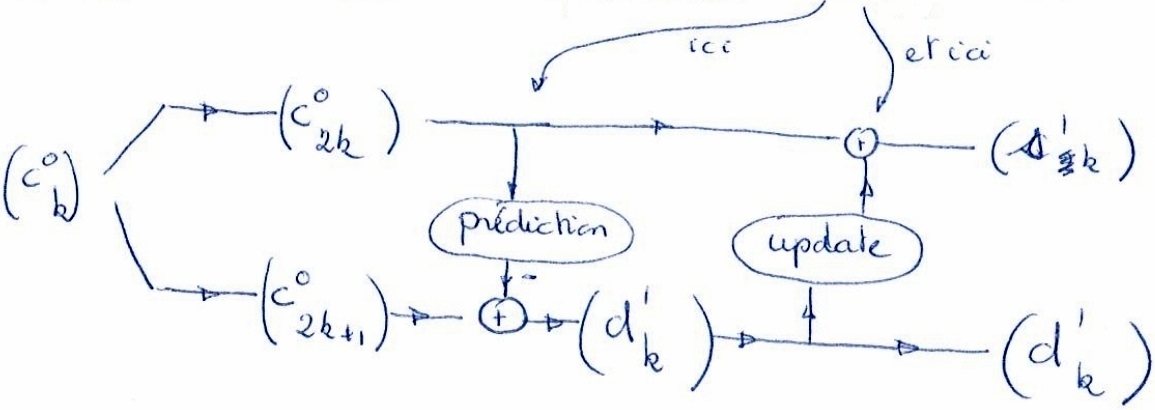
One can very well use nonlinear operations (utilized in B) or adaptative ones (as in C).
• finally, by introducing more than 2 steps if necessary, one can factor into triangular steps all wavelet filters of that sort (see D) — that’s the implementation that was integrated into JPEG2000 because it is so easy.
II. Irregular subdivision
This setting is an example where Sweldens (and I) have looked first at a mathematical problem to see if its solution would suggest an algorithm. With my student Igor Guskov, who joined us early on in this effort, we made a detailed study (papers E and F) in dimension 1, which then suggested to Igor the 2d (surface) construction in his thesis, and also the applications spelled out in paper G (joint with Schröder).
III. Normal meshes
Here we proceeded in the opposite direction. A beautiful idea was first implemented (with spectacular results) — see article H, and then it piqued my mathematical curiosity — see article I (a preprint, not yet on Sweldens’ web page). We are hoping that a more concerted mathematical effort will lead us to other 2d algorithms.
However, this interminable letter must come to an end if it’s to be of any use to you, so I’ll finish now, two days and two pens later, with
hugs and kisses,
Ingrid
\[ \star\qquad\star\qquad\star \]
Cher Yves,
Alors que j’étais en train depuis plus d’une heure à taper un long e-mail pour toi, mon Netscape a rendu l’âme et tout le message est perdu. Tu me diras qu’il y a une justice divine — que c’est ma punition pour ne pas t’avoir répondu plus tôt. Du coup je rédige ceci à la main (au moins tu auras les accents que je n’ai toujours pas maîtrisés sur mon clavier qui ne les a pas), et j’inclus des photocopies des articles dont je parle.
Je m’excuse encore de ne pas avoir répondu plus tôt à tes
e-mails. Tu as raison: c’est une corvée que l’on te demande, et
j’avais dû tout de suite te rendre la tâche la plus facile
possible. Je n’avais pas pu l’anticiper: je ne savais pas que
Björn
t’avait mis sur la liste des noms suggérés au Dean. (Mais ce n’est
pas vraiment une bonne excuse: Björn
m’avait demandé 5 ou 6 noms,
et je lui en avais donné 2 tout de suite, en lui disant que
j’émailerais les autres\ldots et puis j’ai oublié.) Je me suis
demandée aussi pourquoi tu pourrais avoir des problèmes pour
regarder une page à Lucent: il se peut que ce soit parce qu’il y
aurait un blocage pour des pays autres que les E-U. En tous cas,
voici l’addresse sur le réseau qui marche pour moi:
http://wim.sweldens.com
\begin{array}{c}\hline\qquad\qquad\qquad\end{array} (Je continue 2 jours plus tard, après mon coup de fil le 27 mars.) Je te faxerai cettre lettre, comme convenu, et je te l’enverrai aussi “en dur”, accompagnée des articles dont je parle dans la lettre.
Le Dean, et à travers lui, le Committee on Appointments and Tenure, ne s’attendent pas à une discussion approfondie de ta part de tous les aspects de son travail. En fait, ils ont choisi des experts (ou Engquist et Dobkin ont choisi pour eux) dans les différents domaines. Tu peux donc très bien dire dès le départ que tu n’addressera que certaines facettes de sa production scientifique, laissant les autres à d’autres experts.
Du point de vue des Math. App. à Princeton, nous sommes depuis plusieurs années à la recherche de quelqu’un qui intéresserait conjointement le Dépt de Computer Sciences et nous, mais il y avait clairement un mis-match. Les personnes que j’avais proposées quand j’étais directeur, comme Rokhlin, Engquist, Bill Cook et même Adelman, de MIT, ne les intéressaient pas du tout ou seulement modérément; ils étaient plus chauds pour Greengard (qui lui ne voulait pas quitter NYU), mais ils contre-proposaient surtout des gens que nous considérions comme beaucoup moins forts, comme Eric Gross [sic], ou dans des branches moins intéressantes (comme Demmel — gros programmes d’algèbre linéaire). Pour Wim Sweldens par contre, il y a de l’interêt des deux côtés: les “graphicistes” en informatique sont très impressionnés par son palmarès à SIGGRAPH, une conférence qui à autant de participants (4,000 environ) et autant de prestige en graphics que ICM pour les mathématiciens. En général, un exposé à ICM suffit largement, et sans aucune discussion, pour obtenir la tenure dans un “top department” dans ce domaine. D’autre part, il y a aussi de l’intérêt dans notre groupe, pas seulement de ma part (sinon je ne l’aurais jamais proposé), mais aussi de la part de Björn Engquist et Weinan E, qui ont eu des discussions très productives avec lui.
\begin{array}{c}\hline\qquad\qquad\qquad\end{array}
Ce que je trouve le plus intéressant dans Wim, et ce qui constitue pour moi la raison principale pour son attrait comme un pont entre les math. app. et l’informatique, est qu’il comprend très bien l’intuition mathématique, et qu’il est intéressé non seulement par des codes ou programmes que marchent bien, mais aussi par une étude des raisons mathématiques pour leur succès (comme moi, il est persuadé qu’un bon code ne requiert pas seulement de la “cuisine” — bien qu’elle joue un rôle aussi — mais aussi, et principalement, des idées essentiellement mathématiques. Par exemple: intégrer selon la méthode de Lebesgue donne un algorithme de loin supérieur à l’algorithme de Riemann.) Par conséquent, il est toujours intéressé d’explorer l’aspect mathématique de certains développements, même s’il faut parfois, simplifier drastiquement (dans un premier à bord) la description, au-delà de ce que d’autres informaticiens trouveraient raisonnable. Et dans mes collaborations, il a souvent sa part des idées cruciales, même si le côté technique mathématique retombe plus souvent sur moi.
\begin{array}{c}\hline\qquad\qquad\qquad\end{array}
J’attache ici la liste de ses publications. J’en ai marqué quelques-unes que je veux décrire ci-dessous. J’incluerai leurs copies dans le paquet que je t’enverrai. Ces articles illustrent trois “thèmes” dans mon “dossier Sweldens” pour toi, tous dans le cadre interaction math app \( \leftrightarrow \) algorithmes.
\begin{array}{c}\hline\qquad\qquad\qquad\end{array}
I. Lifting
“Lifting” est le nom donné par Sweldens à une construction qui permet de dériver des filtres d’ondelettes plus longs à partir d’autres, plus courts. Dans son stade le plus primitif, il s’agit d’une simple observation algébrique: \begin{equation}\label{eqtw} \eqalign{ \text{si }\quad & m_0 (\xi)\quad \text{ et } \quad \tilde{m}_0(\xi) \text{ satisfont }\cr & m_0 (\xi) \, \overline{\tilde{m}_0 (\xi)} + m_0(\xi + \pi)\, \overline{\tilde{m}_0 (\xi+\pi)} =1, \tag{*} } \end{equation} et on définit \[ m^{\#}_0 (\xi)=\tilde{m}_0(\xi) + e^{-i\xi} \alpha (2\xi)\, \overline{m_0\,(\xi+\pi)}, \] où \( \alpha \) est un polynôme trigonométrique arbitraire, alors la paire \( m_0 \) et \( m^\#_0 \) satisfont \eqref{eqtw} également. Cette observation a été faite pour plusieurs personnes indépendemment: Sweldens, Dahmen & Micchelli, Herley & Vetterli — et somme toute, c’est une observation assez triviale. Ils ont tous aussi observé que les ondelettes splines biorthogonales peuvent être générées à partir de la paire triviale \( m_0 = \frac{1}{\sqrt{2}} \), \( \tilde{m}_0 = \frac{1}{\sqrt{2}} \) en 2 étapes: \( m,\tilde{m}_0 \rightarrow m_0, m^{\#}_0\rightarrow m^b_0, m^{\#}_0 \) (opération duale). La différence entre le travail de Sweldens et les autres est l’interprétation qu’il a donnée (en termes de prédiction et update — voir article A) qui alors permettait plusieurs généralisations et applications très utiles:
• algorithme “in-place”: par ex. dans Haar:
alg. standard:
\[
\eqalign{
c^0_k \longrightarrow s^1_k &= \frac{c^0_{2k} + c^0_{2k+1}}{2}\cr
d^1_k &= c^0_{2k+1} - c^0_{2k}}\quad
\text{(non normalisés).}
\]
Il faut garder les \( c^0_{2k} \), \( c^0_{2k+1} \) en mémoire après le
calcul de \( s^1_k \), pour pouvoir calculer \( d^1_k \).
\smallbreak
alg. lifting:
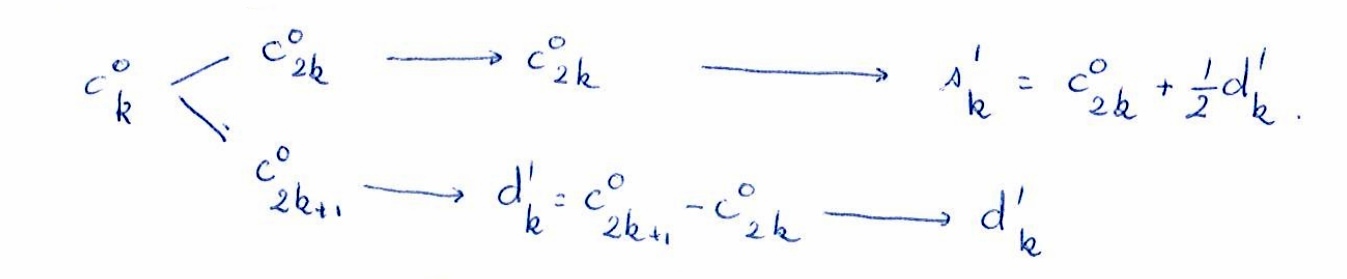
À chaque cacul: une quantité est remplacée par une autre (\( c^0_{2k+1} \) par \( d^1_k \), plus tard \( s^1_k \) par \( c^0_{2k} \)).
Ceci permet de faire des calculs beaucoup plus gros et dans des cadres où la “prédiction” et le “update” ne sont pas uniformes, commes dans l’[sic]
• application à des surfaces et triangulations non-uniformes (voir article A: second-generation wavelets)
• dans le cadre des 2 opérations triangulaires
II. Subdivision irrégulière
Ce cadre-ci est un exemple où Sweldens (et moi) avons regardé d’abord un problème mathématique pour voir si sa solution suggérerait un algorithme. En 1d, nous avons fait, avec Igor Guskov, mon étudiant, qui nous a joints très vite dans cet effort, une étude détaillée (papiers E et F) qui a alors suggéré à Igor la construction en 2d (surface) dans sa thèse, et des applications détaillées dans papier G (joint avec Schröder).
III. Normal meshes
Ici, le cheminement inverse a été fait. Une idée très belle a d’abord été implémentée (avec des résultats spectaculaires) — voir article H, et a ensuite excité ma curiosité mathématique — voir article I (un preprint, pas encore sur la page web de Sweldens). Nous espérons que des travaux math. plus poussés nous amèneront à d’autres algorithmes en 2d.
Cette lettre interminable doit cependant se terminer si je veux qu’elle te soit de quelque utilité, donc je termine, 2 jours et 2 bics plus tard, avec
des grosses bises,
Ingrid