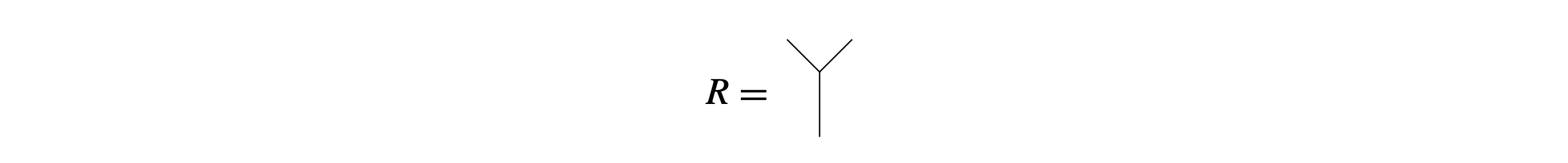Celebratio Mathematica — Jones

On Jones’ connections between
subfactors, conformal field theory,
Thompson’s groups and knots

by Arnaud Brothier

1. A promenade from subfactors to CFT meeting Thompson’s group on the way

From the very beginning the work of Jones has been motivated by and connected to mathematical physics. His theory of subfactors is linked to quantum field theory and in particular to chiral conformal field theory (CFT), which has been formalized in various ways, such as vertex operator algebras or conformal nets. Those latter mathematical objects give subfactors, and some subfactors provide conformal nets. It is by trying to find a systematic reconstruction that Jones unexpectedly met Richard Thompson’s groups \( F \) and \( T. \)

We will tell this story and its repercussions by first presenting subfactors, Thompson’s groups, CFT and explaining how they all became linked together. We will then introduce Jones’ technology for constructing actions of Thompson’s groups and will mainly focus on unitary representations. Finally, we will present how this latter framework led to a connection between Thompson’s groups and knot theory.

1.1. Subfactors

Subfactors are inclusions of von Neumann algebras with trivial center, which are called factors. They carry a rich algebraic structure (the standard invariant) that can be axiomatized — thanks to a reconstruction theorem due to Popa — and is described, for instance, by Jones’ planar algebra [1], [e10], [e13]. Structures like groups, subgroups and quantum groups can be encoded via subfactors, but also more exotic structures naturally appear in that context. Note that the Jones polynomial (the celebrated knot/link invariant) was defined using standard invariants of subfactors, creating a long bridge from operator algebras to low-dimensional topology [2]. Planar algebras are algebraic structures for which elements are composed in the plane rather than on a line. Compositions are encoded by planar diagrams that look like string diagrams used for monoidal categories. It is a collection of sets \( (P_n,\, n\geq 0) \) (usually some finite-dimensional C*-algebras) that is a representation of the planar operad. Hence, any planar tangle like the following:

defines a map where, informally, one can place inside the inner discs some elements of the \( P_n \) (where \( n \) must be the number of boundary points) giving a new element of \( P_m \) with \( m \) the number of boundary points of the outer disc. Hence, the last diagram gives a map from \( P_2\times P_3 \) to \( P_3 \). Gluing tangles by placing one into an inner disc of another provides an associative composition of maps and one can modify tangles by isotopy without changing the associated map.

1.2. Thompson’s groups

Richard Thompson defined three groups \( F\subset T\subset V \), sometimes called chameleon groups for good reason, where \( F \) is the group of piecewise linear homeomorphisms of the unit interval with slopes powers of 2 and finitely many breakpoints at dyadic intervals [e11]. Elements of \( F \) map one (standard dyadic) partition into another in an order-preserving way, being affine on each subinterval. Larger groups \( T,V \) are defined similarly but their elements are allowed to permute subintervals of the associated partitions in a cyclic way, or in any possible way, respectively. In particular, \( T \) still acts by homeomorphisms but on the circle rather than on the interval. Those groups have been extensively studied as they naturally appeared in various fields of mathematics such as infinite group theory, homotopy and dynamical systems, and follow very unusual behavior [e5], [e12]. A famous open problem is to decide whether \( F \) is amenable or not, but even more elementary questions are still open, such as whether \( F \) is exact or weakly amenable in the sense of Cowling and Haagerup [e7]. It is surprising to meet those discrete groups while considering very continuous structures like CFT and subfactors, but we will see that \( T \) appears as a discretization of the conformal group. Moreover, elements of \( T \) can be described by diagrams of trees, suggesting a connection with Jones’ planar algebras and thus with subfactors.

1.3. From CFT to subfactors and back

For us, a conformal net or a CFT is the collection of field algebras localized on intervals of the circle (spacetime regions), on which the diffeomorphism group acts, and that is subject to various axioms coming from physics [e9]. Representation theory of a conformal net looks like very much the algebraic data of a subfactor and one wants to know how similar they are. From a conformal net one can reconstruct a subfactor. However, the converse is fairly mysterious and only specific examples have been worked out, missing the most fascinating ones: the exotic subfactors (subfactors not coming from quantum groups). It is a fundamental question whether such a reconstruction always exists (“Does every subfactor have something to do with a CFT?”) and Jones has been trying very hard to answer it [3], [e21], [e23]. One of his attempts started as follows [4]: given a subfactor we consider its planar algebra \( P=(P_n,\, n\geq 0) \). The idea is then to interpret the outer boundary of a planar tangle as the spacetime circle of a CFT. Given any finite subset \( X \) of the dyadic rationals of the unit disc we consider \( P_X \), a copy of \( P_{|X|} \), where all boundary points on the outer disc of planar tangles are in \( X \). This \( X \) provides a partition of the unit disc. We want to be able to refine this partition \( X \) into a thinner one \( Y \) by adding middle points and to embed \( P_X \) inside \( P_Y \) (giving us a directed system). This is done using a fixed element \( R\in P_4 \) that we think of as a trident-like diagram:

Here is one example that explains how we build a map \( P_X\to P_Y \). Consider a finite subset of points \[ \textstyle X:=\bigl\{0,\frac18,\frac14,\frac12,\frac34\bigr\} \] of the circle identified with the torus \( \mathbb{R}/\mathbb{Z} \). Placing those points on the disc we obtain a partition with intervals \[ \textstyle \bigl(0,\frac18\bigr),\ \bigl(\frac18,\frac14\bigr),\ \ldots,\ \bigl(\frac34,1\bigr). \] Let us refine this partition by splitting the two consecutive intervals \( \bigl(0,\frac18\bigr) \) and \( \bigl(\frac18,\frac14\bigr) \) in two equal halves. This refined partition is characterized by the larger subset of points \[ \textstyle Y:=X\cup \bigl\{\frac1{16},\frac3{16}\bigr\} \] in which we added the middle points of \( \bigl(0,\frac18\bigr) \) and \( \bigl(\frac18,\frac14\bigr). \) Consider a planar tangle with one inner disc. Place the points of \( X \) on the inner disc and the points of \( Y \) on the outer disc. For common elements of \( X \) and \( Y \) we draw a straight line from the inner to the outer disc. In order to connect the two new points of \( Y \) we use our trident-like diagram. We obtain the following tangle:

By definition of the planar operad this tangle encodes a map from \( P_X \) to \( P_Y \) and under a certain condition on \( R \) this latter map is injective. Continuing this process of refinement of finite partitions we obtain at the limit the dense subset of dyadic rationals of the circle and obtain an obvious notion of support defining localized field algebras exactly like in (physics) lattice theory. Moreover, we can rotate and perform some local scale transformations but only using those behaving well with dyadic rationals. This group of transformation is none other than Thompson’s group \( T. \) Moreover, the tree-diagram description of elements of \( T \) can be explicitly used to understand this action simply by sending a branching of a tree to a trident \( R \) in the planar algebra. We obtain some kind of discrete CFT with \( T \) replacing the diffeomorphism group and field algebras localized on intervals of the circle. At this point, the hope was to perform a continuum limit and obtain an honest CFT but unfortunately strong discontinuities arise and the CFT goal was out of reach [5]; see also [e29].

The story could have stopped here but in fact this failed attempt opened whole new fields of research in both mathematics and physics. Indeed, accepting that the continuum limit cannot be done provides physical models relevant at a quantum phase transition with Thompson’s group for symmetry [6], [e28]. Moreover, Jones’ construction paired with models in quantum loop gravity leads to lattice-gauge theories, again with Thompson’s group symmetry [e30], [e27]. The physics described by Jones mathematical model is rather discontinuous and predicts different phenomena than CFT. Jones suggested the following laboratory experiment which would confront the two theories: set up a quantum spin chain and observe the correlation number associated to small translations. Approach a quantum phase transition. According to CFT the correlation number stays close to 1 but Jones’ model with Thompson group for symmetry predicts that this number becomes small. On the mathematical side, Jones discovered a beautiful connection between knot theory and Thompson’s groups by using the planar algebra of Conway tangles [9]. Moreover, he provided a whole new formalism for constructing unitary representations and evaluating matrix coefficients for Thompson’s groups that generalizes the planar algebraic construction [5].

2. Actions and coefficients

After presenting how Thompson’s groups were found in between subfactors and CFT we now present the general theory for constructing groups and actions from categories and functors that we illustrate with Thompson’s groups. Note that this formalism was not developed for the sake of generality but rather to understand better Thompson’s group and other related structures. Jones’ research is driven by the study of concrete and fundamental objects in mathematics such as Temperley–Lieb–Jones algebras, Haagerup’s subfactor, Thompson’s groups, braid groups, etc. His approach is to use or create whatever formalism is pertinent for better understanding those objects, leading to brand new theories like subfactor theory, planar algebras and today Jones actions for groups of fractions. We follow Jones’ attitude by presenting a general formalism but always accompanied by key examples and applications.

2.1. Groups of fractions

The general idea is that a category gives a group and a functor an action. Our leading example is the category \( \mathcal{F} \) of finite ordered rooted binary forests where the objects are the natural numbers and morphisms \( \mathcal{F}(n,m) \), the set of forests with \( n \) roots and \( m \) leaves that we consider as diagrams with roots on the bottom and leaves on top. Composition is obtained by vertical concatenation. For example,

It has been observed that an element of Thompson’s group \( F \) is described by an equivalence class \( t/s \) of pairs of trees \( (t,s) \) having the same number of leaves, where the class \( (t,s) \) is unchanged if we add a common forest on top of each tree [e6], [e11]. This comes from the identification between finite binary rooted trees and standard dyadic partitions of the unit interval. We often described this pair with two trees: \( s \) on the bottom and \( t \) reversed on top. For example, if

The group structure is given by the formula \[ \frac{t}{s}\cdot \frac{s}{r} = \frac{t}{r} \] and thus \[ \biggl(\frac{t}{s}\biggr)^{\!-1} = \frac{s}{t}. \] This corresponds to formally inverting trees and considering morphisms from 1 to 1 inside the universal groupoid of the category of forests \( \mathcal{F} \), where the group \( F \) is identified with the automorphism group of the object 1 inside this latter groupoid. Groups arising in this way are called groups of fractions. Considering trees together with cyclic permutations (affine trees) or all permutations (symmetric trees) we obtain the larger Thompson’s groups \( T \) and \( V \) and if we consider forests with \( r \) roots instead of trees we get Higman–Thompson’s groups. Taking braids, we obtain the braid groups, and taking a topological space as a collection of objects with paths (up to homotopy) for morphisms we get the Poincaré group. All of this was observed long ago in a categorical language in [e1] and for the particular example of Thompson’s groups [e6] that was rediscovered in different terms by Jones.

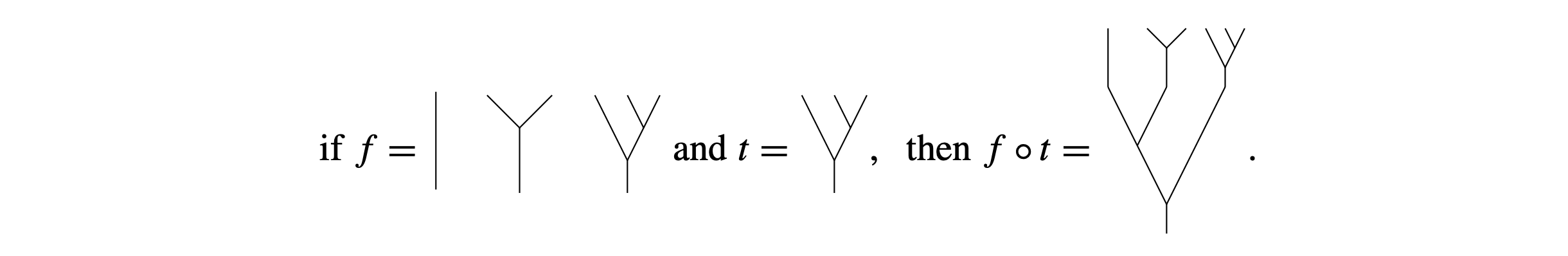
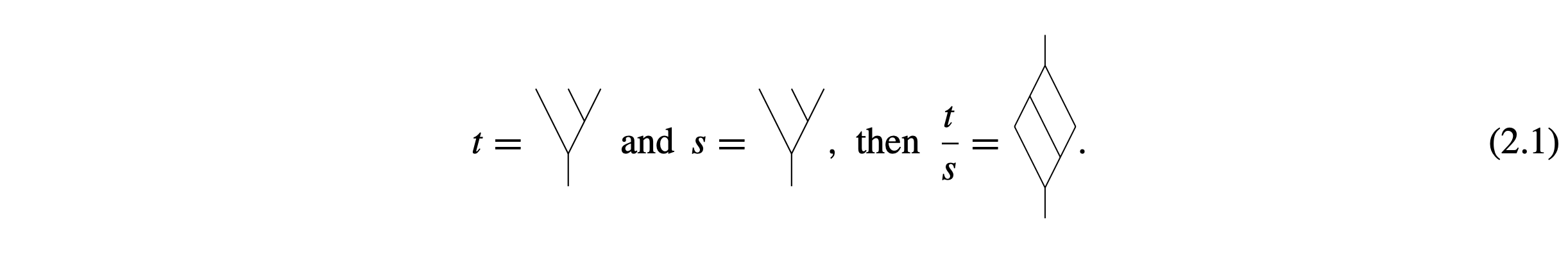
2.2. Jones actions

Jones found a machine to produce in a very explicit manner actions of groups of fractions. Given a functor \( \Phi:\mathcal{F}\to\mathcal{D} \) he constructed an action \( \pi:F\curvearrowright X \) that we call a Jones action. Formally, for a covariant functor and a target category with sets for objects, the space \( X \) is the set of fractions \( t/x \) that are classes of pairs \( (t,x) \) with \( t \) a tree, \( x\in\Phi(n) \) with \( n \) being the number of leaves of \( t \) and where the equivalence relation is generated by \[ (t,x)\sim (ft,\Phi(f)x) \] for any forest \( f \). The Jones action is then defined as \[ \pi\biggl(\frac{s}{t}\biggr) \frac{t}{x} = \frac{s}{x}. \] We sometimes want to complete this space with respect to a given metric, and this is what we do if \( \mathcal{D} \) is the category of Hilbert spaces. Observe that \( X \) is defined in the same way as the group of fractions except that now the denominator is in the target category and the equivalence relation is defined using the functor \( \Phi. \) Making \( \mathcal{F} \) monoidal by declaring that the tensor product of forests is the horizontal concatenation, we obtain that \( \mathcal{F} \) is generated by the single morphism \( Y, \) i.e., the tree with two leaves. Hence, (monoidal) functors \( \Phi:\mathcal{F}\to\mathcal{D} \) correspond to morphisms \[ R:=\Phi(Y)\in\operatorname{Hom}_\mathcal{D}(a, a\otimes a) \] in the target category \( \mathcal{D} \). In particular, a Hilbert space \( \mathfrak{H} \) and an isometry \[ R:\mathfrak{H}\to\mathfrak{H}\otimes\mathfrak{H} \] provide a unitary representation of Thompson’s group that we call a Jones representation. Using string diagrams to represent morphisms in a monoidal category we can interpret a functor \( \Phi:\mathcal{F}\to\mathcal{D} \) as taking the diagram of a forest and associating the exact same diagram but in the different environment of the target category \( \mathcal{D} \). This procedure is nothing other than replacing each branching in a forest by an instance of the morphism \( R \):

Note that for technical reasons we might use morphisms with four boundary points rather than three (if, for instance, one wants to work with subfactor planar algebras or Conway tangles that only have even numbers of boundary points) and thus consider a map of the form

We give credit to Jones for those actions, even if some of the ideas were already around; however, the construction with a direct limit was completely new. We are grateful to Matt Brin for a very nice explanation of the state of the art before Jones’ work. “What was known was that certain automorphism groups contained Thompson’s groups. How they acted was never under investigation and the fact that the actions could be manipulated to get desired properties never even occurred to anyone.”

2.2.1. Planar algebraic examples

Let us compute some coefficients with this technique. Start with a planar algebra \( P \) with a one-dimensional 0-box space (diagrams without boundary points correspond to numbers) and choose an object

satisfying

Assume that \( P \) is equipped with an inner product which consists of connecting two elements of \( P_n \) via \( n\text{ strings} \) like

Then \( R \) defines a unitary representation and moreover has a favorite vector called the vacuum vector corresponding to a straight line in the planar algebra. The positive definite function associated to the vacuum vector \( \Omega \) is then a closed diagram inside \( P \) which is equal to the following if we consider the group element \( t/s \) of (2.1):

but viewed inside \( P \) where it corresponds to a number (via the partition function). This number can be explicitly computed using skein relations (diagrammatic rules for reducing diagrams, such as (2.2), analogous to relations for a presented group) of the planar algebra chosen. Jones called them wysiwyg representations (“what you see is what you get”) [8]. Planar algebras have been extensively studied in the past two decades and we know today many interesting examples with fully understood skein relations providing candidates for wysiwyg representations. Using a certain class of planar algebras, (trivalent categories studied by Peters, Morrison and Snyder [e20]), Jones constructed an uncountable family of mutually inequivalent wysiwyg unitary representations that are all irreducible.

Those latter examples emanate from the planar algebraic approximation of CFT and keep some geometric flavor. Next we present examples that somehow forget the geometric structure of planar algebras but can be defined in a very elementary way.

2.2.2. Analytic examples

Let us consider the whole category of Hilbert spaces \( \operatorname{Hilb} \) with isometries for morphisms. There are various monoidal structures \( \odot \) we can equip \( \operatorname{Hilb} \) with such as the classical tensor product or the direct sum. Free products can also be done but one has to consider a slightly different category where objects are pointed Hilbert spaces \( (H,\xi) \), where \( \xi \) is a unit vector and morphisms are isometries sending the chosen unit vector to the other one; see [e8]. Each case provides Jones representations by taking an isometry \[ R:\mathfrak{H}\to\mathfrak{H}\odot\mathfrak{H} \] for the chosen monoidal structure \( \odot \). The second case can be written as \( R=A\oplus B \) with \( A,B:\mathfrak{H}\to\mathfrak{H} \) satisfying the Pythagorean identity \begin{equation} \tag{2.4} \label{eq:Pyth}A^*A+B^*B=1. \end{equation} We call the Pythagorean algebra the universal C*-algebra generated by this relation and observe that a representation of this latter algebra provides a Jones representation of Thompson’s groups [10]. Moreover, it has interesting quotient algebras such as the Cuntz algebra, noncommutative tori, and Connes–Landi spheres [e2], [e3], [e4], [e14]. Taking any unit vector \( \xi\in \mathfrak{H} \) we obtain a positive definite function as matrix coefficient. It can be computed as follows. Consider an element of \( F \) written \( t/s \). Place \( \xi \) at the root of \( s \) and make it go to the top by applying \( A\oplus B \) at each branching. We obtain on top of each leaf a word in \( A,B \) applied to \( \xi \). We do the same thing for \( t \) and then take the sum of the inner product at each leaf. For example, if \( t/s \) is the example of (2.1) we obtain the inner product \[ \langle A\xi \oplus AB\xi \oplus BB\xi , AA\xi\oplus BA \xi \oplus B\xi\rangle \] and the procedure in making \( \xi \) going from the bottom to the top of the tree \( s \) is described by the following diagram:

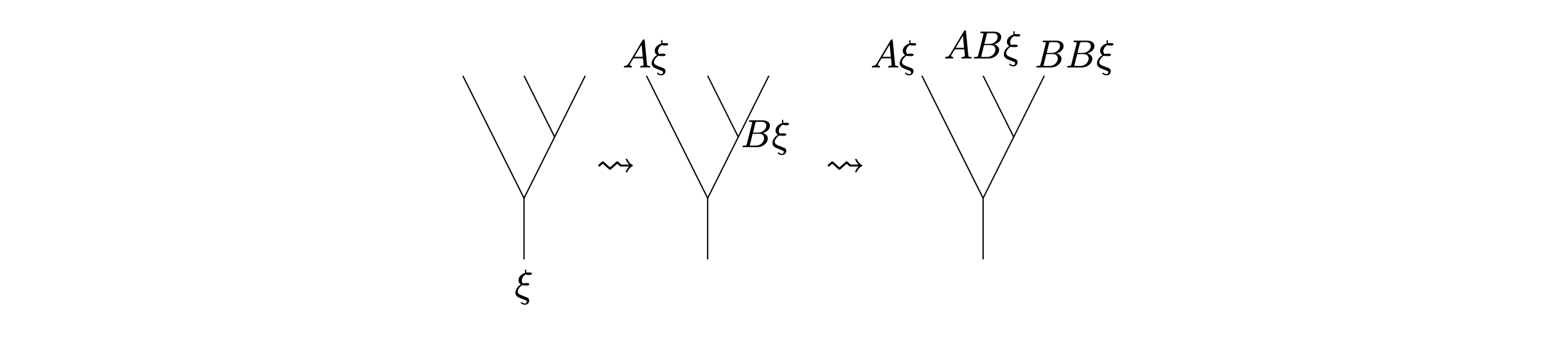
The formula of this coefficient for elements of the larger group \( T \) is similar up to permuting cyclically the order of the vectors in the direct sum and can be extended to \( V \) by considering any permutations. Many interesting representations and coefficients of Thompson’s groups can be created in that way. If \( A=B \) are real numbers equal to \( 1/\sqrt 2 \), then we recover the Koopman representation \( T\curvearrowright L^2(\mathbb S^1) \) induced by the usual action of \( T \) on the circle. In more detail: fix a tree \( s \) and a complex number \( \xi \). Following the procedure explained by the diagram above we obtain that each leaf \( \ell \) of \( s \) is decorated by \( 2^{-d^\ell_s/2} \xi \), where \( d_s^\ell \) is the distance from the leaf to the root. This latter number corresponds to \( \xi \) times the square root of the length of the interval \( I_s^\ell \) associated to the leaf. Taking a second tree \( t \) such that \( g=t/s\in F \) we obtain that the contribution of the inner product associated to \( \xi=1 \) and \( g \) at a leaf \( \ell \) is \( 2^{(d^\ell_s-d^\ell_t)/2} \) that is the square root of the slope of \( g \) when restricted to \( I_s^\ell \). From this observation it is not hard to conclude. Thanks to the flexibility of Jones’ formalism, we can easily deform this representation by replacing \( 1/\sqrt 2 \) by two different real or complex numbers \( v \) and \( w \) with \( |v|^2+|w|^2=1 \) obtaining various paths between the Koopman and the trivial representations where the former appears when \( v \) or \( w \) is equal to zero. Using the free group we obtain the map \[ g\in F\mapsto \operatorname{Measure}(x\in (0,1) : gx=x) \] as a diagonal matrix coefficient, and it is then positive definite. Other examples arise by taking representations of quotients of the Pythagorean algebras, providing interesting families of representations. One can also use this approach for constructing representations of such quotient algebras: with the help of Anna Marie Bohman and Ruy Exel, Jones and I could relate precisely representations of the Cuntz and the Pythagorean algebras, obtaining new methods for practical constructions of representations of the former.

If we choose the monoidal structure to be the classical tensor product of Hilbert spaces, then any isometry \[ R:\mathfrak{H}\to\mathfrak{H}\otimes\mathfrak{H} \] provides a unitary representation of \( V \). Matrix coefficients associated to \( \xi,\eta\in\mathfrak{H} \), \[ \biggl\langle \pi\biggl(\frac{t}{s}\biggr) \xi,\eta\biggr\rangle, \] can be computed as above but where we need to perform an inner product of two vectors in a tensor power of \( \mathfrak{H} \) instead of a direct sum, where each tensor power factor corresponds to a leaf of the tree \( t \). Interesting and manageable examples arise when \( R\xi \) is a finite sum of elementary tensors and thus matrix coefficients are then computed in an algorithmic way. Here is one story concerning those representations and how they can be manipulated and used.

During February 2018 Jones and I met one week in the beautiful coastal town of Raglan in New Zealand to finish up the paper on Pythagorean representations and to enjoy the kite-surf spot a bit. During this stay Jones told me that the absence of Kazhdan property (T) for \( F,T,V \) could be trivially proved via his recent formalism. Indeed, this can be done using maps like \[ R\xi=u\xi\otimes\zeta , \] where \( \zeta \) is a fixed unit vector and \( u \) an isometry. For example, this map and the pair of trees \( t/s \) of (2.1) give the following matrix coefficient: \[ \biggl\langle \pi\biggl(\frac{t}{s}\biggr) \zeta , \zeta \biggr\rangle = \langle u\zeta\otimes u\zeta\otimes \zeta , u^2\zeta\otimes \zeta\otimes \zeta\rangle = |\langle \zeta,u\zeta\rangle|^2. \] By considering a family of those pairs \( (u,\zeta) \) and making \( \langle u\zeta,\zeta\rangle \) tend to 1, we obtain an almost invariant vector but no invariant one in the associated Jones representation.

Moreover, he showed me how to create the left regular representation of \( F \) via a tensor product construction where \( \mathfrak{H}=\ell^2(\mathbb N) \) and \[ R\delta_n=\delta_{n+1}\otimes\delta_{n+1}=\delta_{n+1,n+1}. \] Indeed, if \( t \) is a tree, then using the functor \( \Phi \) we get \( \Phi(t)\delta_0 = \delta_{w_t}, \) where \( w_t \) is the list of distances between each leaf of \( t \) to its root. Since this characterizes the tree \( t \) we obtain that the cyclic component of the Jones representation associated to the vector \( \delta_0 \) is the left regular representation of \( F \).

Those two facts made me very excited. Showing that Thompson’s groups are not Kazhdan groups is a difficult result that stayed open for quite some time. Jones’ proof being so effortless gave hope to obtain stronger results with more elaborate techniques. The regular representation has coefficients vanishing at infinity and thus one might be able to construct others of that kind. For this purpose we started to think about deforming the isometry \( R\delta_n=\delta_{n+1,n+1} \), obtaining paths between the trivial and the left regular representations and new coefficients. Going back home during the very long journey from Raglan to Rome I only thought about those deformations. When I landed I had more or less a full proof showing that \( T \) has the Haagerup property improving the absence of the Kazhdan property but only for the intermediate Thompson’s group \( T \). I wrote to Jones about it and we decided to write a short paper giving the two proofs: \( F,T,V \) are not Kazhdan groups and \( T \) has the Haagerup property [11]. Even though those results are not optimal and already known (Farley showed that \( V \) has the Haagerup property [e16]) they display the power of Jones’ new techniques. One intriguing fact is that the maps constructed by Farley (the one associated to his cocycle) coincide with ours on Thompson’s group \( T \) but differ on the larger group \( V \) and it is still unclear how to build them using Jones representations. Another interesting problem would be to construct Farley actions on CAT(0) cubical complexes via Jones actions using the appropriate target category [e15].

A year later, new results were proved regarding analytical properties of groups. Choose a group \( \Gamma \) and a single group morphism \[ g\in\Gamma\mapsto (a_g,b_g)\in\Gamma\oplus\Gamma. \] This provides a (monoidal) functor from the category of forests to the category of groups and thus a Jones action of \( V \) on a limit group. One can then consider the semidirect product. Choosing the trivial embedding \( g\in\Gamma\mapsto (g,e) \) we obtain the (permutational and restricted) wreath product \( \bigoplus_{\mathbb{Q}_2} \Gamma\rtimes V \), where \( V \) shifts the indices via the usual action \( V\curvearrowright \mathbb{Q}_2 \), where \( \mathbb{Q}_2 \) is the set of dyadic rationals on the unit circle. Now comes a trivial but key observation: this new group can be written as a group of fractions where the new category is basically made of forests but with leaves labeled by elements of \( \Gamma. \) Composition of forests with group elements in this latter category, constructed with the map \( g\mapsto (a_g,b_g) \), is expressed by the equality

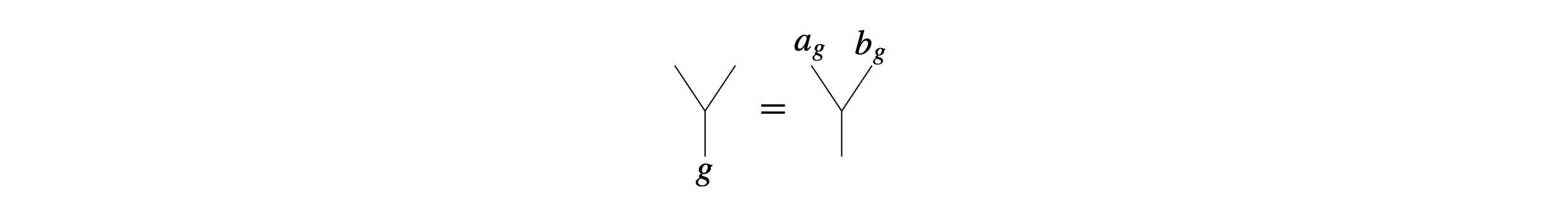
Note that a similar construction was observed by Brin using Zappa–Szép products, which he used to define the braided Thompson’s group [e18]; see also [e17]. Since it is a group of fractions, we can then apply Jones’ technology for constructing representations and coefficients of this larger group. Using this strategy I was able to show that those wreath products have the Haagerup property when \( \Gamma \) has it, which was out of reach by other known approaches [e26].

2.3. Connection with knot theory

Knot theory and Thompson’s groups are connected using the technology presented above. This has been very well explained in a recent expository article of Jones so I will be brief [9]. The connection comes from the idea to consider functors from forests to the category of Conway tangles that are roughly speaking strings inside a box possibly attached to the top and/or the bottom that can cross like

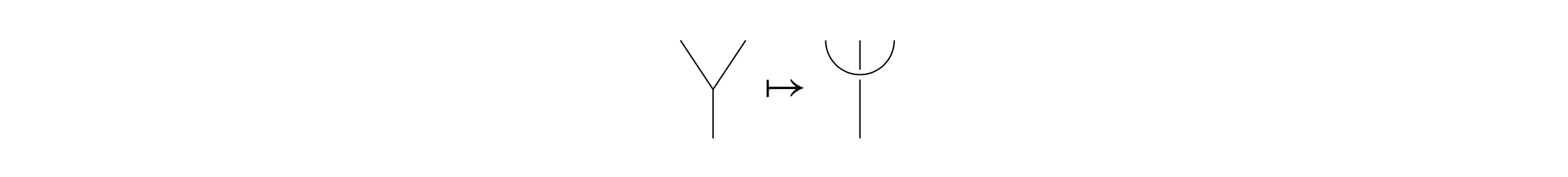
We ask that those diagrams be invariant under isotopy and the three Reidemeister moves. We define a functor from (binary) forests to Conway tangles by replacing each branching by one crossing as follows:

Consider an element of \( g=t/s\in F \) with \( t,s \) trees, where we put \( s \) on the bottom, \( t \) upside down on top and connect their roots. We then apply our transformation that replaces each branching by a crossing obtaining a link.

The procedure is the following for the example of (2.1):

Smoothing out this diagram we obtain the following knot:

Jones proved the theorem that every link can be obtained in that way, concluding that “Thompson’s group is as good as the braid groups for producing links”. This opened a completely new land of study in which Jones already suggested nine explicit research problems which explore the group structure analogy between Thompson’s and braid groups ([9], Section 7). Examples of problems are finding a Markov theorem for Thompson (what are the relations between two Thompson’s group elements that give the same link) or deciding the Jones–Thompson index of a link (what is the minimal number of leaves necessary for a couple of trees to form this link). This latter index for links can be defined for \( k \)-ary trees, \( k\geq 2 \), instead of binary trees, giving a discrete-parameter family of invariants for links.

The connection with links provided a new point of view on Thompson’s group elements. One can then ask whether the link associated to an element of \( F \) is orientable or not. It turns out that the set of all \( g\in F \) giving an orientable link forms a subgroup \( \vec F\subset F \) known today as the Jones subgroup. This subgroup can be defined in a number of ways using diagram groups, skein theory, stabilizers and is even equal to a group of fractions [4], [e19], [e22], [7]. Golan and Sapir were able to prove the striking result that \( \vec F \) is isomorphic to Thompson’s group \( F_3 \) associated to 3-adic numbers and moreover is equal to its commensurator, implying that the associated quasiregular representation is irreducible [e19]. The different definitions of \( \vec F \) suggested various natural generalizations of it: a circular Jones subgroup \( \vec T\subset T \); from the diagram group approach Golan and Sapir obtained an increasing chain of subgroups \( \vec F_n\subset F, \) \( n\geq 2; \) and the stabilizer definition provided an uncountable family \( F_{(I)}\subset F \) parametrized by the famous Jones’ range of indices for subfactors \[ \biggl\{4\cos\biggl(\frac{\pi}n\biggr)^{\!2}: n\geq 4\biggr\}\cup [4,\infty) \] [1]. Using skein theory of planar algebras Ren interpreted differently \( \vec F \) reproving that it is isomorphic to \( F_3 \) and interestingly, he and Nikkel showed that \( \vec T \) is not isomorphic to \( T_3 \) but is similar from a diagram-group perspective [e22], [e24]. Golan and Sapir proved properties for the subgroups \( \vec F_n\subset F \) similar to those for \( \vec F\subset F \), obtaining an infinite family of irreducible representations and isomorphisms \( \vec F_n \simeq F_{n+1} \) (Thompson’s group associated to \( (n+1) \)-adic numbers) [e19]. The uncountable family of \( F_{(I)} \) is less exciting as it generically provides trivial subgroups, except of course for \( \vec F \) which corresponds to the first nontrivial Jones’ index 2 [e25]. The Jones subgroup \( \vec F \) and the study around it summarize well the interplay of various fields in this brand new framework of Jones and how ideas, say from knot theory or skein theory, can be then applied in group theory and vice versa.

3. Conclusion

The recent technology of Jones regarding Thompson’s groups has provided new perspectives and connections for and between groups of fractions, knot theory, subfactor theory and quantum field theory. This complements previous beautiful connections that Jones made more than 35 years ago with his celebrated polynomial. This is only the very beginning of this development and various exciting research directions remain untouched. There have been already beautiful applications and promising techniques developed which augur a bright future.

References

[e1] P. Gabriel and M. Zisman: Calculus of fractions and homotopy theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 35. Springer-Verlag (New York), 1967. MR 210125 book

[e2] J. Cuntz: “Simple \( C^* \)-algebras generated by isometries,” Comm. Math. Phys. 57 : 2 (1977), pp. 173–185. MR 467330 article

[e3] A. Connes: “\( C^{\ast} \) algèbres et géométrie différentielle,” C. R. Acad. Sci. Paris Sér. A-B 290 : 13 (1980), pp. A599–A604. MR 572645 article

[e4] M. A. Rieffel: “\( C^{\ast} \)-algebras associated with irrational rotations,” Pacific J. Math. 93 : 2 (1981), pp. 415–429. MR 623572 article

[e5] M. G. Brin and C. C. Squier: “Groups of piecewise linear homeomorphisms of the real line,” Invent. Math. 79 : 3 (1985), pp. 485–498. MR 782231 article

[e6] K. S. Brown: “Finiteness properties of groups,” pp. 45–75 in Proceedings of the Northwestern conference on cohomology of groups, published as J. Pure Appl. Algebra 44 : 1–3 (1987). MR 885095 incollection

[e7] M. Cowling and U. Haagerup: “Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one,” Invent. Math. 96 : 3 (1989), pp. 507–549. MR 996553 article

[e8] D. V. Voiculescu, K. J. Dykema, and A. Nica: Free random variables: A noncommutative probability approach to free products with applications to random matrices, operator algebras and harmonic analysis on free groups. CRM Monograph Series 1. Amer. Math. Soc. (Providence, RI), 1992. MR 1217253 book

[e9] D. E. Evans and Y. Kawahigashi: “Subfactors and conformal field theory,” pp. 341–369 in Quantum and non-commutative analysis (Kyoto, 1992). Math. Phys. Stud. 16. Kluwer (Dordrecht), 1993. MR 1276304 incollection

[e10] S. Popa: “An axiomatization of the lattice of higher relative commutants of a subfactor,” Invent. Math. 120 : 3 (1995), pp. 427–445. MR 1334479 article

[e11] J. W. Cannon, W. J. Floyd, and W. R. Parry: “Introductory notes on Richard Thompson’s groups,” Enseign. Math. (2) 42 : 3–4 (1996), pp. 215–256. MR 1426438 article

[e12] M. G. Brin: “The chameleon groups of Richard J. Thompson: automorphisms and dynamics,” Inst. Hautes Études Sci. Publ. Math. 84 (1996), pp. 5–33. MR 1441005 article

[e13] V. F. R. Jones: Planar algebras, I. Preprint, 1999. ArXiv 9909027 techreport

[e14] A. Connes and G. Landi: “Noncommutative manifolds, the instanton algebra and isospectral deformations,” Comm. Math. Phys. 221 : 1 (2001), pp. 141–159. MR 1846904 article

[e15] D. S. Farley: “Finiteness and \( \rm CAT(0) \) properties of diagram groups,” Topology 42 : 5 (2003), pp. 1065–1082. MR 1978047 article

[e16] D. S. Farley: “Proper isometric actions of Thompson’s groups on Hilbert space,” Int. Math. Res. Not. 45 (2003), pp. 2409–2414. MR 2006480 article

[e17] P. Dehornoy: “The group of parenthesized braids,” Adv. Math. 205 : 2 (2006), pp. 354–409. MR 2258261 article

[e18] M. G. Brin: “The algebra of strand splitting. I. A braided version of Thompson’s group \( V \),” J. Group Theory 10 : 6 (2007), pp. 757–788. MR 2364825 article

[e19] G. Golan and M. Sapir: “On Jones’ subgroup of R. Thompson group \( F \),” J. Algebra 470 (2017), pp. 122–159. MR 3565428 article

[e20] S. Morrison, E. Peters, and N. Snyder: “Categories generated by a trivalent vertex,” Selecta Math. (N.S.) 23 : 2 (2017), pp. 817–868. MR 3624901 article

[e21] M. Bischoff: “The relation between subfactors arising from conformal nets and the realization of quantum doubles,” pp. 15–24 in Proceedings of the 2014 Maui and 2015 Qinhuangdao conferences in honour of Vaughan F. R. Jones’ 60th birthday. Proc. Centre Math. Appl. Austral. Nat. Univ. 46. Austral. Nat. Univ. (Canberra), 2017. MR 3635667 inproceedings

[e22] Y. Ren: “From skein theory to presentations for Thompson group,” J. Algebra 498 (2018), pp. 178–196. MR 3754410 article

[e23] F. Xu: “Examples of subfactors from conformal field theory,” Comm. Math. Phys. 357 : 1 (2018), pp. 61–75. MR 3764563 article

[e24] J. Nikkel and Y. Ren: “On Jones’ subgroup of R. Thompson’s group \( T \),” Internat. J. Algebra Comput. 28 : 5 (2018), pp. 877–903. MR 3844705 article

[e25] V. Aiello, A. Brothier, and R. Conti: “Jones Representations of Thompson’s Group F Arising from Temperley–Lieb–Jones Algebras,” International Mathematics Research Notices 10 (2019), pp. rnz240. article

[e26] A. Brothier: Haagerup property for wreath products constructed with Thompson’s groups. Preprint, 2019. ArXiv 1906.03789 techreport

[e27] A. Brothier and A. Stottmeister: Canonical quantization of 1+1-dimensional Yang-Mills theory: An operator-algebraic approach. Preprint, 2019. ArXiv 1907.05549 techreport

[e28] T. J. Osborne and D. E. Stiegemann: Quantum fields for unitary representations of Thompson’s groups F and T. Preprint, 2019. ArXiv 1903.00318 techreport

[e29] A. Kliesch and R. König: “Continuum limits of homogeneous binary trees and the Thompson group,” Phys. Rev. Lett. 124 : 1 (2020), pp. 010601, 5. MR 4053920 article

[e30] A. Brothier and A. Stottmeister: “Operator-algebraic construction of gauge theories and Jones’ actions of Thompson’s groups,” Comm. Math. Phys. 376 : 2 (2020), pp. 841–891. MR 4103960 article

Works

[1] V. F. R. Jones: “Index for subfactors,” Invent. Math. 72 : 1 (1983), pp. 1–25. A lecture based on this was published in Fields Medallists’ lectures (1997). MR 696688 Zbl 0508.46040 article

[2] V. F. R. Jones: “A polynomial invariant for knots via von Neumann algebras,” Bull. Am. Math. Soc. 12 : 1 (January 1985), pp. 103–111. A lecture based on this was published in Fields Medallists’ lectures (1997). MR 766964 Zbl 0564.57006 article

[3] V. F. R. Jones, S. Morrison, and N. Snyder: “The classification of subfactors of index at most 5,” Bull. Am. Math. Soc. (N.S.) 51 : 2 (2014), pp. 277–327. MR 3166042 Zbl 1301.46039 ArXiv 1304.6141 article

A subfactor is an inclusion \( N\subset M \) of von Neumann algebras with trivial centers. The simplest example comes from the fixed points of a group action \( M^G \subset M \), and subfactors can be thought of as fixed points of more general group-like algebraic structures. These algebraic structures are closely related to tensor categories and have played important roles in knot theory, quantum groups, statistical mechanics, and topological quantum field theory. There is a measure of size of a subfactor, called the index. Remarkably, the values of the index below 4 are quantized, which suggests that it may be possible to classify subfactors of small index. Subfactors of index at most 4 were classified in the 1980s and early 1990s. The possible index values above 4 are not quantized, but once you exclude a certain family, it turns out that again the possibilities are quantized. Recently, the classification of subfactors has been extended up to index 5, and (outside of the infinite families) there are only 10 subfactors of index between 4 and 5. We give a summary of the key ideas in this classification and discuss what is known about these special small subfactors.

Noah Snyder	Related
Scott Morrison	Related

[4] V. Jones: “Some unitary representations of Thompson’s groups \( F \) and \( T \),” J. Comb. Algebra 1 : 1 (2017), pp. 1–44. MR 3589908 Zbl 06684911 ArXiv 1412.7740 article

[5] V. F. R. Jones: “A no-go theorem for the continuum limit of a periodic quantum spin chain,” Comm. Math. Phys. 357 : 1 (2018), pp. 295–317. MR 3764571 Zbl 1397.82025 ArXiv 1607.08769 article

[6] V. F. R. Jones: “Scale invariant transfer matrices and Hamiltonians,” J. Phys. A 51 : 10 (2018). article no. 104001, 27 pages. MR 3766219 Zbl 1387.82010 ArXiv 1706.00515 article

Given a direct system of Hilbert spaces \( s\mapsto \mathcal{H}_s \) (with isometric inclusion maps \[ \iota_s^t:\mathcal{H}_s\rightarrow \mathcal{H}_t \] for \( s\leq t \)) corresponding to quantum systems on scales \( s \), we define notions of scale invariant and weakly scale invariant operators. In some cases of quantum spin chains we find conditions for transfer matrices and nearest neighbour Hamiltonians to be scale invariant or weakly so. Scale invariance forces spatial inhomogeneity of the spectral parameter. But weakly scale invariant transfer matrices may be spatially homogeneous in which case the change of spectral parameter from one scale to another is governed by a classical dynamical system exhibiting fractal behaviour.

[7] V. Aiello, R. Conti, and V. F. R. Jones: “The Homflypt polynomial and the oriented Thompson group,” Quantum Topol. 9 : 3 (2018), pp. 461–472. MR 3827807 Zbl 1397.57022 ArXiv 1609.02484 article

Roberto Conti	Related
Valeriano Aiello	Related

[8] V. F. R. Jones: Irreducibility of the Wysiwyg representations of Thompson’s groups. Preprint, June 2019. ArXiv 1906.09619 techreport

[9] V. F. R. Jones: “On the construction of knots and links from Thompson’s groups,” pp. 43–66 in Knots, low-dimensional topology and applications: Knots in Hellas (Olympia, Greece, 17–23 July 2016). Edited by C. C. Adams, C. M. Gordon, V. F. R. Jones, L. H. Kauffman, S. Lambropoulou, K. C. Millett, J. H. Przytycki, R. Ricca, and R. Sazdanovic. Springer Proceedings in Mathematics & Statistics 284. Springer (Cham, Switzerland), 2019. MR 3986040 Zbl 1423.57013 ArXiv 1810.06034 incollection

Renzo Luigi Ricca	Related
Radmila Sazdanović	Related
Józef Henryk Przytycki	Related
Cameron McAllan Gordon	Related	Volume
Kenneth C. Millett	Related
Louis H. Kauffman	Related
Colin C. Adams	Related
Sofia S. F. Lambropoulou	Related

@incollection {key3986040m,
	AUTHOR = {Jones, Vaughan F. R.},
	TITLE = {On the construction of knots and links
		 from {T}hompson's groups},
	BOOKTITLE = {Knots, low-dimensional topology and
		 applications: {K}nots in {H}ellas},
	EDITOR = {Adams, Colin C. and Gordon, Cameron
		 McA. and Jones, Vaughan F. R. and Kauffman,
		 Louis H. and Lambropoulou, Sofia and
		 Millett, Kenneth C. and Przytycki, Jozef
		 H. and Ricca, Renzo and Sazdanovic,
		 Radmila},
	SERIES = {Springer Proceedings in Mathematics
		 \& Statistics},
	NUMBER = {284},
	PUBLISHER = {Springer},
	ADDRESS = {Cham, Switzerland},
	YEAR = {2019},
	PAGES = {43--66},
	DOI = {10.1007/978-3-030-16031-9_3},
	NOTE = {(Olympia, Greece, 17--23 July 2016).
		 ArXiv:1810.06034. MR:3986040. Zbl:1423.57013.},
	ISSN = {2194-1009},
	ISBN = {9783030160302},
}

[10] A. Brothier and V. F. R. Jones: “Pythagorean representations of Thompson’s groups,” J. Funct. Anal. 277 : 7 (October 2019), pp. 2442–2469. MR 3989149 Zbl 07089431 ArXiv 1807.06215 article

[11] A. Brothier and V. F. R. Jones: “On the Haagerup and Kazhdan properties of R. Thompson’s groups,” J. Group Theory 22 : 5 (2019), pp. 795–807. MR 4000616 Zbl 07104291 ArXiv 1805.02177 article

A machinery developed by the second author produces a rich family of unitary representations of the Thompson groups \( F \), \( T \) and \( V \). We use it to give direct proofs of two previously known results. First, we exhibit a unitary representation of \( V \) that has an almost invariant vector but no nonzero \( [F,F] \)-invariant vectors reproving and extending Reznikoff’s result that any intermediate subgroup between the commutator subgroup of \( F \) and \( V \) does not have Kazhdan’s property (T) (though Reznikoff proved it for subgroups of \( T \)). Second, we construct a one parameter family interpolating between the trivial and the left regular representations of \( V \). We exhibit a net of coefficients for those representations which vanish at infinity on \( T \) and converge to 1 thus reproving that \( T \) has the Haagerup property after Farley who further proved that \( V \) has this property.