by R. S. MacKay
1. Introduction
Colin’s interest in cosmology came to my attention when I saw that he would give the first Warwick Mathematics Institute colloquium in our new building (December 2003), with title “A new paradigm for the universe”. In the end, the safety checks had not yet been completed, so he gave it in the old building. Nonetheless, to mark the occasion, the Physics Department kindly presented a photograph showing the new building at the centre of the universe (actually, the centre of the M31 galaxy) (Figure 1).
To summarise Colin’s talk, here is the abstract for the paper he put
on arXiv the month before
[1]:
A new paradigm for the structure of galaxies is proposed. The main hypothesis is that a normal galaxy contains a hypermassive black hole at its centre which generates the spiral arms. The paradigm gives satisfactory explanations for:
- the rotation curve of a galaxy;
- the spherical bulge at the centre of a normal galaxy;
- the spiral structure and long-term stability of a normal galaxy;
- the age and orbits of globular clusters;
- the origin and prevalence of solar systems;
- (highly speculative) the origin of life.
The paradigm is compatible with direct observations but not with many of the current interpretations of these observations. It is also incompatible with large swathes of current cosmological theory and in particular with the expanding universe and hot big-bang theories. A tentative new explanation for the observed redshift of distant objects is given which is compatible with a static model for the universe. This paper is being circulated in a very preliminary form in the hope that others will work both on interpreting observational data in the light of the new paradigm and on the obvious gaps in underlying theory.
Far reaching! Subsequently, Colin developed his ideas further, including firming up the promised explanation of redshift. It culminated in a book The Geometry of the Universe [6], which forms the basis for this review.
I found Colin’s talk somewhat whacky, but several aspects resonated with me, in particular that the big-bang story is over-simplistic, that redshift could have alternative explanations, and that dark matter is wild speculation. So I took up his invitation “to help complete the work” [1] and we began talking about it.
2. Galaxies
Colin’s paradigm starts with galaxies. In particular, he proposed that they have a hypermassive black hole at their centre. This might not sound revolutionary, because it was proposed more than 50 years ago [e6]. Furthermore, images have been produced recently of the gas cloud around proposed black holes at the centres of the Messier 87 galaxy and our own one (Figure 2). But although the mass of the observed black hole Sgr A\( ^* \) in the Milky Way is estimated at 4 million solar masses, Colin’s proposal is that there is one of around \( 10^{11}-10^{12} \) solar masses in a different location (revised down from his earlier estimate of \( 10^{15} \) solar masses but still much larger than the standard one).
He proposed that galaxies with spiral arms are around \( 10^{12}-10^{16} \) years old, longer than the time since the big bang (standardly estimated at \( 13.8 \times 10^9 \) years ago), thereby challenging the big-bang story. Amusingly, observations from the recently launched James Webb space telescope are showing distant galaxies as they were 400–500 million years after the big bang, for example, [e21] and Figure 3, but containing stellar populations that according to some look over a billion years old [e22] (though much scorn has been poured on that article). So Colin is not alone today in questioning the big-bang story.
A key ingredient of Colin’s new paradigm for galaxies is an inertial-drag effect due to rotation of the central black hole. Einstein’s general relativity is known to produce inertial-drag effects, that is, Coriolis and centrifugal forces in frames that do not appear to be rotating. In particular, the Lense–Thirring effect makes an effective frame-rotation rate \( \omega= \mathrm{G}J/(\mathrm{c}^2r^3) \) at distance \( r \) from a rotating black hole of angular momentum \( J \) (where \( \mathrm{G} \) is the gravitational constant and \( c \) the speed of light), and this has been confirmed by observations [e19]. But Colin’s proposed effect has \( \omega = \mathrm{G}M\Omega/(\mathrm{c}r) \) with mass \( M \) and angular velocity \( \Omega \) of the black hole. He argues for it from Sciama’s version of Mach’s principle, which I’ll review shortly.
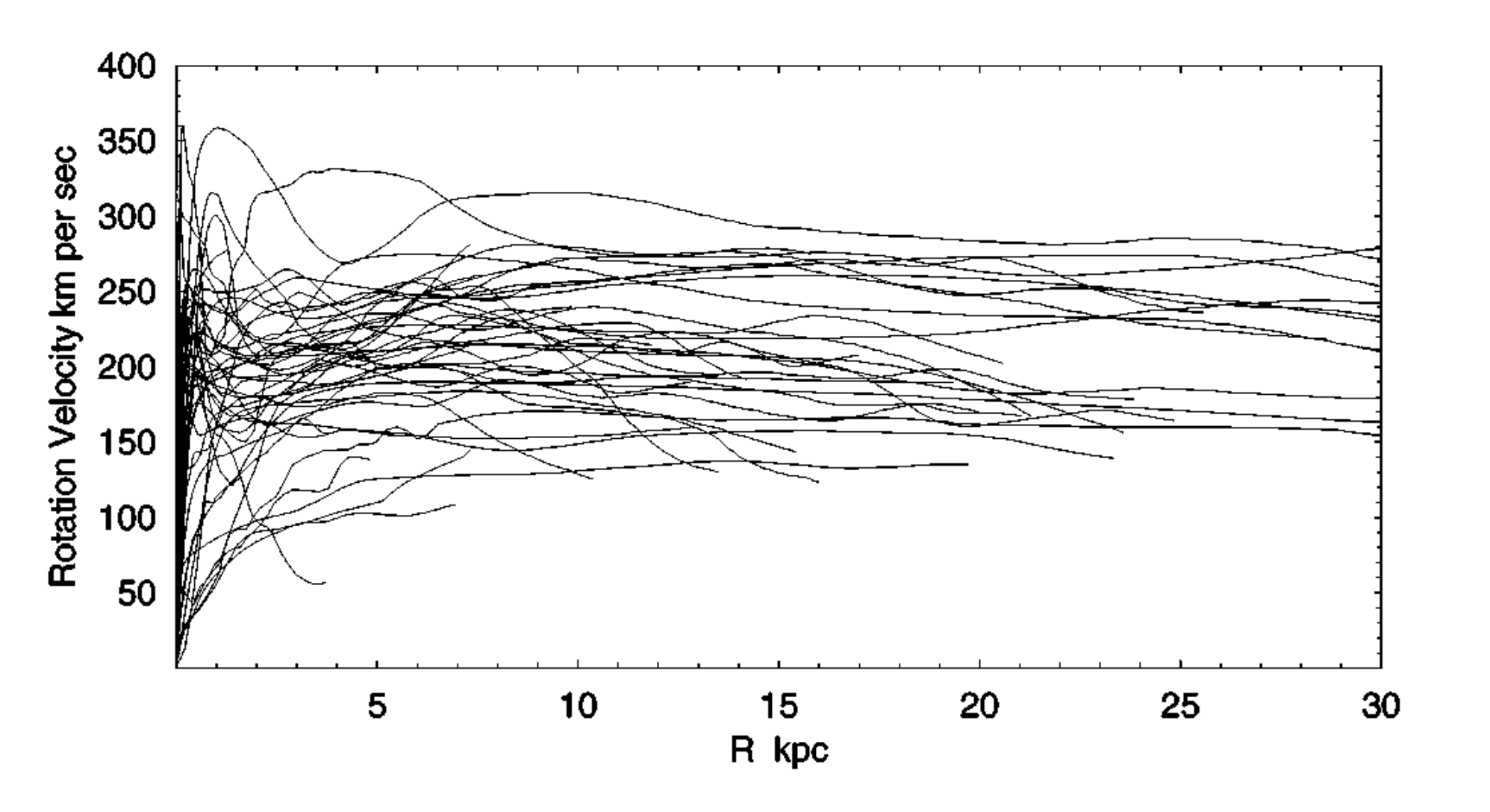
Colin uses this inertial drag law to explain the rotation curves of galaxies and to reinterpret quasars. I’ll address the rotation curves first.
The conundrum of the rotation curves of galaxies is that according to Newtonian gravity the tangential speed of matter outside the main mass of a galaxy should decrease like \( r^{-1/2} \) where \( r \) is the distance from the centre, whereas in practice it is almost constant (at about \( 10^{-3} \) times the speed of light) (see Figure 4). This suggested that there is a lot of invisible mass further out than the visible core. Named “dark matter”, it is an innocuous proposal (why should all matter be visible?) except that no-one has managed to detect any of it yet, apart from via its gravitational effect (though again, how else might one hope to detect it?). Dark matter had been proposed in 1933 by Zwicky to explain failure of observations of visible matter to fit the virial theorem (though with later observations it seems the discrepancy is much smaller). It has also been found to be an essential ingredient for the standard model of the universe: to fit observations of redshift as a function of luminosity distance (Hubble’s law) and the cosmic microwave background, \( 27\% \) of the mass in the universe is proposed to be dark matter (see [e15], for example).
Sciama’s version of Mach’s principle is that “the statement that the Earth is rotating and the rest of the universe is at rest should lead to the same dynamical consequences as the statement that the universe is rotating and the Earth is at rest” [e2]. Thus, rotation of bodies in the universe should produce Coriolis effects. Mach’s principle is plausible but appears incompatible with Einstein’s general relativity, despite having been part of the inspiration for it. So Colin is making a modification to standard physics here. But he is in good company: Sciama was an outstanding physicist, PhD student of Dirac and supervisor of many influential cosmologists, including Stephen Hawking. On the other hand, Mach’s principle has also been addressed by Pietronero [e8], who derived a frame-dragging effect \( \omega = {\mathrm{G}M^{\prime}\Omega/\mathrm{c}} \) at the axis of a rotating cylinder of mass \( M^{\prime} \) per unit length from general relativity and argued that this is a realisation of Mach’s principle. A natural question is what is the effect outside the cylinder? Does it decay like \( 1/r \) (just as in Newtonian gravity, the potential inside a spherical shell is constant and decays like \( 1/r \) outside)? Still, let us follow the implications of Colin’s proposed frame-dragging law.
Colin’s explanation of rotation curves gives asymptotic tangential
speed \( \mathrm{G}M\Omega/\mathrm{c}^2 \) (in units of \( \mathrm{c} \)) for large \( r \). Observations
show that it has much the same value (around \( 10^{-3} \)) for all
galaxies, so a remaining challenge is to explain this value of
\( M\Omega \). Note that \( \Omega \) is not an observable quantity in
standard theory of black holes: only the mass \( M \) and angular momentum
\( J \) are defined, not its angular velocity \( \Omega \). Yet, there are
natural notions of the radius of a black hole, for example, the Schwarzschild
radius \( R_s = 2\mathrm{G}M/\mathrm{c}^2 \).
So Colin quite reasonably writes \( J = M\Omega
k^2 R_s^2 \) for some factor \( k \) of order 1, and hence deduces
\[
\Omega = \frac{\mathrm{c}^4 J}{4\mathrm{G}^2M^2k^2}.
\]
Then Colin’s tangential speed is \( \mathrm{c}^2
J/(4k^2\mathrm{G}M) \). Noting the limit \( J \le \mathrm{G}M^2/\mathrm{c}^2 \) for Kerr solutions with
an event horizon, Colin’s theory could correspond to black holes
choosing their angular momentum to be a factor about \( 10^{-3} \) from
the Kerr limit. But is there a reason? Furthermore, it is claimed from
observations
[e9]
that the asymptotic speed for the rotation
curve is proportional to the fourth root of the luminosity; Colin does
not give much weight to this fit, but could it be explained by his
theory?
3. Quasars
Next, Colin used his inertial drag law to give a new interpretation of quasars. These “quasistellar radio sources” are, according to standard theory, large black holes (up to \( 10^{11} \) solar masses) surrounded by a gaseous accretion disk that radiates electromagnetic energy converted from part of the kinetic energy of infalling gas. They are considered to be at large distances, thereby explaining their large redshifts. Colin proposes (reviving a view discussed 60 years ago but rejected [e4]) that they might be closer and considerably less massive, with their redshift resulting from the radiation taking place from a small radius about the black hole and being redshifted as it climbs out (gravitational redshift). Colin’s key idea is that his frame-dragging law allows the black hole to absorb angular momentum from the gas, which otherwise was a known obstacle to theories along this line. He thereby proposed that to obtain a rough idea of the process it is enough to consider radial infall onto a spherically symmetric black hole and to suppose that the kinetic energy of infalling gas is converted to radiation coming principally from the Eddington radius, which is the location where radiation pressure provides the acceleration necessary to stop the infall. Colin refutes the objections to this interpretation in considerable detail.
Colin drafted a paper on his model for quasars [5], asking our joint PhD student Rosemberg Toalá-Enríquez and me to fill in some parts. I still haven’t managed the parts Colin asked me to do (making a realistic model for the profiles of density, temperature and ionisation fraction, to find the principal location from which the radiation comes), nor did I understand sufficiently Colin’s proposal about ignoring angular momentum, and I felt somewhat uncomfortable having my name on the draft, so resisted for a while but he prevailed. Rereading it now, I understand his argument better. It would still be good to examine his proposal in more detail (see the Appendix to this review).
4. The HLSW law
As can be inferred from his abstract, another important topic of Colin’s work is reinterpreting Hubble’s law. Hubble’s law is that the radiation received from objects is redshifted by an amount proportional to their luminosity distance.
First, Colin makes some comments on nomenclature. It was acknowledged by the International Astronomical Union in 2018 that credit for Hubble’s law should be shared with Lemaître. Colin and I certainly share this view and I have followed some of Lemaître’s history. Figure 5 shows the college in Leuven where he lived around this time (the Katholieke Universiteit had a college system with a history to rival Oxbridge’s). Colin argues that the discovery of the law goes back to Slipher and Weyl, so he refers to it as the HLSW law. Certainly, Lemaître used Slipher’s observational data.
The HLSW law is where our collaboration began. First we played around with the thought that it could be a cumulative result of null geodesics passing through fluctuations in the metric; we didn’t reach a conclusion, but see Section 7. Then after a study in spherically symmetric space-times [3], we found that the HLSW law is a feature of all space-times having what we called a “natural observer field” [2] (note that although written after [3], it was published earlier). Perhaps there is a better name, but we defined a natural observer field to be a timelike vector field whose integral curves are geodesic and whose perpendicular plane field is integrable. This generalises the concept of the “Hubble flow”, the vector field on a Friedmann universe pointing purely in the time direction (in “comoving coordinates”), along which all matter is assumed (approximately) to flow (and would be better called the Friedmann flow since it was part of Friedmann’s model). In particular, a natural observer field induces a coherent notion of time: constant on the perpendicular space-slices and whose difference between two space-slices is the proper time along any fieldline.
For any object, radiation emitted at frequency \( \omega_e \) in its frame is received by us at a frequency \( \omega_r \) proportional to \( \omega_e \), by convention written as \( \omega_r = \omega_e/(1+z) \), with \( z \) called the redshift. For space-times with a natural observer field we proved that if we are moving along the observer field, the redshift \( z \) of an object also moving along the observer field is given by \[ \log(1+z) = \int_{t_e}^{t_r} \rho(v(t))\, dt, \] where \( \rho(v) \) is the rate of expansion of space in spatial direction \( v \) along the observer field, \( v(t) \) is the spatial velocity of the null geodesic from the object to us at coherent time \( t \) and \( t_e, t_r \) are the times of emission and reception, respectively. The HLSW law relates the redshift to the luminosity distance \( d_L \). This is the distance such that the received power per unit perpendicular area (in the receiver frame) is the emitted power per unit solid angle (in the emitter frame) divided by \( ((1+z)d_L)^2 \), the factor that one would obtain from the inverse square law and the reduction of power by redshift. For space-times with a natural observer field we obtained \[ d_L = \int_{t_e}^{t_r} (1+z(t))\, dt, \] where \( z(t) \) is the redshift that an observer moving along the observer field would see on crossing the null geodesic at its time \( t \). If \( \rho(v(t)) \) is approximately a constant \( \rho_0 \) along the null geodesics then we derived \( z \approx \rho_0 d_L/\mathrm{c} \), the HLSW law with HLSW constant \( H_0 = \rho_0/\mathrm{c} \).
We found de Sitter space to provide an instructive example [2], [3]. De Sitter space is a solution of Einstein’s equations with positive cosmological constant \( \Lambda \) and negligible matter. It has expanding natural observer fields, namely the velocity field of any bundle of timelike geodesics all backwards asymptotic to each other. Indeed, Weyl [e1] declared that all matter must flow along such a field, else for each object there would be a time up to which it would be invisible to us and after which it would become visible, which he felt to be inconsistent with ideas of determinism (more on this later). These observer fields have constant expansion rate \( \sqrt{\Lambda/3} \) in any direction. Our universe is believed to be in a de Sitter phase [e17], with \( \sqrt{\Lambda/3} \) equal to the HLSW time \( H_0^{-1} \approx 14.4 \times 10^9 \) years, so it is a reasonable model. To include some matter we extended our illustration to Kottler space (also known as Schwarzschild–de Sitter space), which can be considered to be de Sitter space with a single nonrotating black hole (or more precisely an antipodal pair of black holes) [2], [3]. In Kottler space the expansion rate depends on direction.
Then we dropped the constraint of supposing that all matter flows along a natural observer field. Calculating arbitrary time-like geodesics in de Sitter space, and the null geodesics from one to the other, we confirmed that for an emitter-receiver pair in general position there is a receiver time \( t^* \) before which no light is received from the emitter (as anticipated by Weyl), and found there is an interval \( (t^*,t^*+t_B) \) during which light is received blueshifted, and on \( (t^*+t_B,+\infty) \) light is received redshifted and asymptotically satisfying the HLSW law with HLSW constant \( \sqrt{\Lambda/3} \). So the HLSW law could be the result of positive cosmological constant and an observer selection-bias: an emitter is more likely to be seen with a redshift near the HLSW law. A similar conclusion applies to perturbations of de Sitter space.
5. Gamma-ray bursts
Our study of de Sitter space had a remarkable spin-off, namely, it suggested a possible kinematic explanation for gamma-ray bursts (GRB) [4], [7]. These are bursts of intense electromagnetic radiation of cosmic origin that start abruptly, dying out over a few seconds or several minutes (Figure 6), whose frequency starts in the gamma range and decreases. Standard explanations are in terms of cataclysmic events like a black hole eating a neutron star, but we propose a simple kinematic explanation.
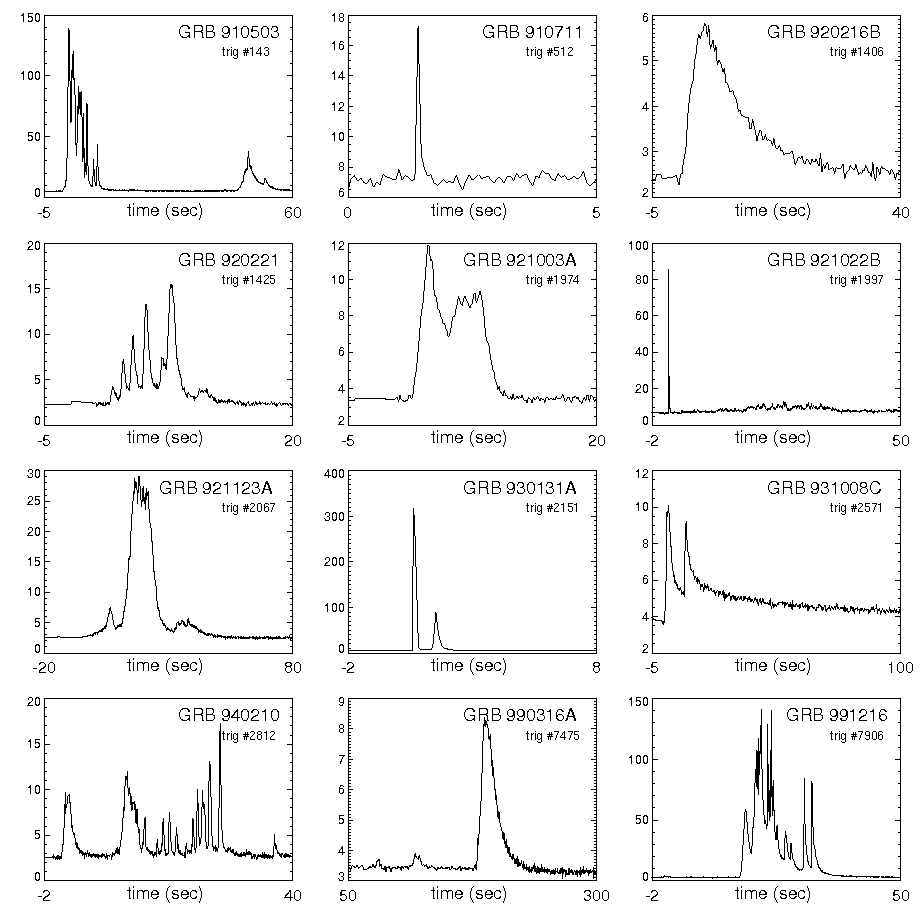
We already had the hint from the analysis that received light in de Sitter space starts blue-shifted. Indeed, it starts infinitely blue-shifted (so, even higher frequencies than gamma-rays). What about its intensity? Call the “intensification” the ratio of received power per unit area to emitted power per unit solid angle. We computed the intensification and found that it starts infinite. Both blue-shift and intensification subsequently decay (with the blue-shift turning to red after the blueshift period \( t_B \)). The typical blueshift period is an HLSW time, which is far too long compared to the observed durations, but we showed that the intensification is much stronger for shorter \( t_B \), and the distribution of \( t_B \) for emitter geodesics chosen uniformly with respect to the natural Haar measure has density like \( t_B^{-5} \). Thus we can expect to see very short \( t_B \). The observations peak around \( t_B \) of the order of 20 seconds and fall off for shorter durations, but this cutoff could have various explanations, on which more later.
More general space-times have similar effects (though not the Friedmann universes with big bang). So we propose that many GRBs are just the natural way that any emitter coming “over the horizon” should look in a non-big-bang universe. This fits with many observations, though is not accepted by the mainstream astrophysics community.
The nonacceptance of our explanation of GRBs was reflected in our attempts to publish. We had a paper on GRB ready in 2011 but it was rejected by the journals we tried over several years. To attempt to get some visibility, we also produced a punchy short version, but it was again rejected by all the places we tried (it is included as Appendix F in [6]). Eventually the long version was accepted as [4]. When I realised I could also explain observations that GRBs are not polarised, I rewrote the short version to include that, but the journals I tried rejected it, and to cap it all, so did arXiv! The best I found so far was to put it on ResearchGate [7].
6. Big bang
As mentioned near the beginning, a central feature of Colin’s work is to reject the big bang. Colin bases this on a number of arguments. One is that there are globular clusters that are dated to be 15 billion years old, thus before the big bang. Another is that the Hubble ultradeep field images show fully formed galaxies so far in the past that he says they did not have time to form.
My take on the big bang is that even if the conditions for the Penrose–Hawking singularity theorems are satisfied, the theorems do not say that everything came out of a singularity, only that there are some incomplete backward geodesics. The strongest version I have seen is that there is a 3-parameter family of incomplete timelike backward geodesics [e7]. That leaves plenty of room for the rest of the universe to keep going backwards as long as it likes.
I believe that the idea that all came from a singularity is due to over-reliance on the Friedmann solutions of general relativity (starting with the “primeval atom” theory of Lemaître, who rediscovered them). They are a special class of solutions in which there is a preferred time-coordinate and the spatial slices are homogeneous and isotropic. Under plausible physical conditions, they shrink to a singularity in finite backwards time. Friedmann’s solutions were a very important step in the understanding of the cosmological consequences of general relativity (in keeping with their importance, they were rediscovered by not only Lemaître but also Robertson and then Walker), but general relativity has many more solutions. In particular, a key consequence of Einstein’s genius was to liberate us from the concept of an absolute time and it is a pity that cosmologists put it back in. In particular, even if there is a preferred velocity field in space-time, in general the perpendicular plane field is not integrable (the Frobenius condition fails) so it does not define spatial slices nor an absolute time. We need to go beyond Friedmann’s solutions (and not just to the various Bianchi universes [e11]).
7. Cosmic microwave background
The largest thing that remains for Colin or successors to firm up is an explanation of the cosmic microwave background (CMB) without a big bang. The standard big-bang story is that the universe was filled by a hydrogen plasma and electromagnetic radiation in approximate equilibrium, but as the universe expanded, the density and temperature fell, and at a temperature of about \( 3000K \) the plasma combined into hydrogen atoms, the coupling between the matter and radiation was lost, and the resulting radiation was redshifted by further expansion by a factor around 1100 to become what we see now as the almost isotropic \( 2.7K \) cosmic microwave background field. Instead, we propose that it is the result of thermalisation of radiation by inhomogeneities in the metric, perhaps in the form of gravitational waves, as outlined in Colin’s book.
Consider the bundle of null geodesics that reach us in some solid angle of directions over the product of some transverse surface (which I will call “aperture”) and time interval. Follow them backwards. It is conventional to talk about going backwards along light rays for a given time or a given distance, but that requires choosing a reference frame. In a Friedmann universe (or with a natural observer field) there is a preferred notion of time, but for a general Lorentzian metric there is not. For time-like geodesics one has an intrinsic notion of time between two points along them, namely the proper time, but the intrinsic time between any two points along a null geodesic is zero. Nonetheless, there is a notion of affine parameter for a null geodesic, that is, a parametrisation that is intrinsic up to shift of origin and linear scaling. We choose to fix the origin of an affine parametrisation to be where the null geodesic crosses the product of the aperture and time interval, and choose the scaling to make the parametrisation agree with our proper time in a local frame.
In general, the bundle of null geodesics diverges as one follows it backwards in affine parameter. At first it diverges linearly because of the solid angle of directions, but further away one can expect typical nearby pairs of null geodesics to separate exponentially because of deviations of the metric from a simple one. This is because the equations for null geodesic flow on a Lorentzian space-time \( M \) with metric \( g \) are a Hamiltonian system in 7D (the flow on the zero-level of the metric \( g^{-1}:T^*M\to \mathbb{R} \) on the cotangent bundle), with the only general symmetry being scaling of the cotangent vectors, so we can expect to see a positive Lyapunov exponent. Indeed, one can expect the bundle of null geodesics to form 5D versions of whorls and tendrils and mix transversely, just like time-dependent stirring of a layer of fluid. So the bundle of null geodesics comes from a spread-out sample of points at early affine parameter, and what we see is an average over such a set.
Furthermore, the frequency spectrum we see is the result of some random redshifting. The redshifting can be described by parallel-transporting the emitter velocity (or the velocity of a frame in which the frequency distribution is known) along the null geodesic to the receiver, where it can be written as \( (\gamma, \gamma v) \) for some \( v \in \mathbb{R}^3 \) and \( \gamma = \sqrt{1-|v|^2/c^2} \). The redshift \( z \) is given by \[ 1+z = \gamma \biggl(1+\frac{|v|}{c}\cos\theta\biggr) \] where \( \theta \) is the angle between \( v \) and the direction of receipt of the null geodesic. Could the result perhaps be a black-body spectrum, with temperature \( T \) corresponding to the radiation density \( U \) by the standard formula \( U=(4/\mathrm{c})\sigma T^4 \) (where \( \sigma \) is Stefan’s constant)? Even if one considers a very small solid angle of initial directions, corresponding to looking in a precise direction, and if one takes a small aperture, what we receive can come from a very spread-out set. Colin makes the analogy with fog, where light paths are scattered a long way from a straight line.
One thing that needs estimating is the Lyapunov time, the affine parameter change for one e-folding in separation of null geodesics, that determines how fast the mixing occurs in backwards time. There is plenty of evidence for optical distortions, some of which is surveyed by Colin in ([6], Appendix E), generally attributed to passage of light rays near something particularly massive or through dark matter distributions, but some of which could be from gravitational waves. Figure 7 shows a more recent example. These distortions are already seen at redshifts of order 1, but more relevant is probably so-called “weak-lensing”, which is distortion due to passage through general inhomogeneities. Objects can be identified to at least \( z=10 \). So one could expect a Lyapunov time somewhat more than this.
After that, the big question is why does the resulting averaged radiation have the observed temperature of \( 2.7 K \)? The temperature would correspond to that of the radiation at the optical depth, modified by the redshift from there to us (note that it seems now standard to use the term “optical depth” for the logarithm of the incident to transmitted power, but I learnt it as the depth to which one can distinguish objects in the visual field, like “visibility” in meteorology, thus corresponding to transmitted power being some fraction like \( 1/e \) of incident).
And can we explain the observed slight anisotropies of the CMB? A big success of standard cosmological theory is to explain them in terms of (principally) acoustic oscillations in the plasma before the transition to atoms [e15], [e18]. Although the theory of the amplitude of acoustic oscillations depends on the hypothetical notion of inflation, we have a steep challenge to do better! Nevertheless, perhaps the spectrum of anisotropies from our mechanism is governed by the same law; the Sachs–Wolfe anisotropy effects of gravitational inhomogeneities (and a variant proposed by Rees and Sciama) are called secondary in the standard theory.
8. Other topics
There is a lot more in Colin’s paper [1] and in his book [6], for example on the structure of galaxies, the abundance of elements, and on quasars and galaxies as life forms. I don’t feel competent to review those, but recommend interested readers to study the book.
It is worth mentioning that there are other books challenging standard cosmology, even by leaders in the field like Roger Penrose [e16] and Steinhardt & Turok [e14]. It seems permitted to such authors to make far wilder speculations than Rourke’s.
9. Colin
I close with some personal remarks about Colin. He is very articulate (I remember him destroying other people’s arguments in staff meetings). He is ready to question received dogma: we need more like him. And it is fun to discuss ideas with him.
Appendix: Comments on Appendix C of “The geometry of the universe” on quasars
As stated in Appendix C of [6], the work on quasars reported there is still in progress and is based on a draft paper [5] that we intend to get into a publishable form one day.
Expanding on what is indicated in his Appendix C, the main thing we felt is needed is a suitable model of the infalling gas to determine profiles of density, temperature and ionisation fraction as functions of radial coordinate. Mestel [e3] gives an idea of what is involved but simplifies by proposing two shells of constant temperature. Our purpose is to find the location from where the outgoing radiation can be considered as coming. It is given by \( r \) for which \[ \sigma_T \int_r^\infty \frac{n_e}{\sqrt{Q}}\, dr \] is of order 1 (in treatments of optical depth it seems conventional to choose \( \tfrac23 \)), where \( n_e \) is the density of electrons and \( \sigma_T \) is the Thomson cross-section for scattering of light by an electron (or possibly modified versions to take into account other scattering processes). The factor \( \sqrt{Q} = \sqrt{1-2M/r} \) is to convert changes in \( r \) to changes in radial distance (\( r \) is the Schwarzschild coordinate such that the sphere at constant \( r \) has area \( 4\pi r^2 \)).
I think there is a simpler problem that needs fixing too, namely, (C.13) needs modifying to \( E(r) = mc^2(1-\sqrt{Q}) \), because the energy received outside is reduced by a factor only \( 1/(1+z) \). This agrees with [e5], for example. It is power that is reduced by \( 1/(1+z)^2 \). But I don’t think this correction has any effect outside section C.4.
I believe also that in (C.6) both the accretion rate \( A \) and the Eddington luminosity need dividing by \( \sqrt{Q} \), because the accretion rate in proper time at radius \( r \) is increased by a factor of \( 1/\sqrt{Q} \) and so is the relativistic Eddington luminosity (see, for example, [e10], [e12]). But this makes no difference to the outcome of (C.6).
