by Rob Kirby
A Heegaard splitting of a closed 3-dimensional manifold \( M^3 \) is a centuries-old [e1] description of \( M \) as a union of two handlebodies with their boundaries (surfaces of genus \( g \)) glued together by a diffeomorphism. The 3-sphere is the union of two 3-balls, or, more interestingly, the union of two donuts (neighborhoods of the unit circle in the xy-plane and the z-axis union infinity). The latter splitting is used to stabilize a Heegaard splitting of \( M \), increasing its genus to \( g+1 \). One can ask if two Heegaard splitting of the same manifold are equivalent; this was proved by Reidemeister [e3] and Singer [e2] to be true after stabilizing.
A Heegaard splitting of \( M \) also arises from a Morse-like function \( f:M\to [0,3] \) where critical points of index \( i \) are mapped to \( i \). Then the Heegaard surface is \( S=f^{-1}(3/2) \). Cerf theory then gives another proof of stabilization because stabilizing amounts to a birth of a cancelling 1–2-pair.
A key question arose: Is one stabilization sufficient or might more stabilizations be necessary to transform one Heegaard genus \( g \) splitting to another? All examples known needed only one stabilization until the Hass–Thompson–Thurston paper [1], which gave examples where \( g \) stabilizations are necessary. These are obtained by switching the two handlebodies, or equivalently turning the Morse function upside down by changing \( f \) to \( -f \).
The main theorem is:
It is always true that \( g \) stabilizations are enough to turn any Heegaard splitting of any closed 3-manifold upside down. A sketch of the argument is given in a remark at the end of the Introduction (Section 2) of [1].
The proof that \( g \) stabilizations are needed embodies a beautiful topological idea which requires subtle geometry involving curvature, volume, area and harmonic maps.
Let \( \Sigma \) be the original genus \( g \) Heegaard surface. Then we stabilize \( \Sigma \) \( k \) times to obtain a Heegaard surface \( S \) of genus \( g+k \), and we want to show that \( k \) must at least equal \( g \).
To turn the Heegaard surface \( S \) upside down, we need an isotopy \( f_s: M \to M, s \in [0,1] \) which takes \( S \) to itself but with the opposite orientation.
\( M \) can be expressed as \( \Sigma \times (-1,1) \) union two spines which are the wedges of \( g \) circles. As \( S \) flips upside down, we have a two parameter family of surfaces, \( S_{s,t}, s\in [0,1], t \in (-1,1) \), where the surface \( S_{s,t} \) is the image of the slice \( S \times t \) under the isotopy \( f_s \) at time \( s \). These surfaces divide \( M \) into two parts, and we color one red and one blue, giving the surface a red and a blue side.
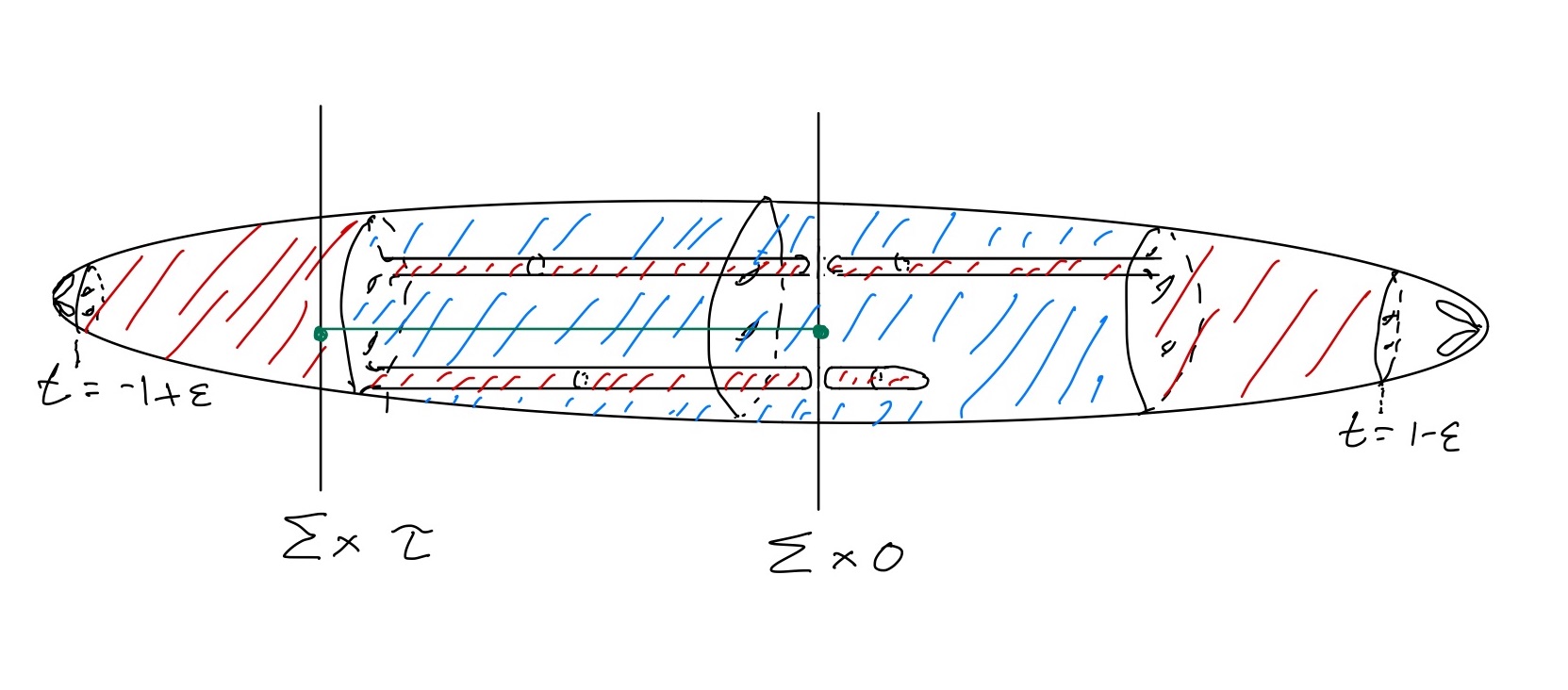
Now choose \( s \) and \( t \) so that the surface \( S_{s,t} \) divides the volume of \( M \) in half. There is a 1-parameter family \( \lambda \) of such surfaces. Consider the two halves, left and right, of \( M \) when cut by \( \Sigma \times 0 \). Then \( (0,0) \) and \( (1,0) \) both belong to \( \lambda \) but with the left side red in the first case, and the right side red in the second case. Thus there must be an \( (s,t) \) for which \( S_{s,t} \) divides the left side in equal parts and similarly the right side (see Figure 1).
Metrics are chosen so that \( \Sigma \times (-1,1) \) is very long and thin. Then because of area and volume bounds, each \( S_{s,t} \) will intersect a high percentage of the \( \Sigma \times t \) in very small circles, each one smaller than the injectivity radius of \( \Sigma \times t \) and thus bounding a disk in \( \Sigma \times t \). All disks will be the same color because their complement is connected (this is only true if the circles are not nested, in which case the argument is slightly more subtle).
Since \( S_{s,t} \) is so thin most of the time, we can assume it is thin at \( \Sigma \times 0 \). Then we can surger each of the small circles at time 0, thus capping off the tubes with disks. Assume these disks cap off red tubes. Now we focus on the left side of \( M \) and find a slice \( \Sigma \times \tau \), at which the tubes are thin and mostly blue (otherwise the volume of the left side would not be divided in half by red and blue regions). Now cap off these disks to get a closed surface \( F \) inside \( \Sigma \times [\tau,0] \).
The key observation now is that we can run a green arc from \( \Sigma \times 0 \) through a red cap, thus intersecting \( F \) in a point and going from a blue region into a red region, and then staying in the red region to its end point at \( \Sigma \times \tau \). The green arc may intersect \( F \) in two more points whenever intersecting a component of \( F \) which encloses a blue region. This green arc intersects \( F \) an odd number of times and hence is homologically dual to \( F \). This means that \( F \) represents \( H_2 (\Sigma \times [\tau ,0],Z/2) \), and thus must have genus greater than or equal to \( g \) because there is no degree one map of a surface of lower genus to a surface of higher genus.
Now we do the same for the right side, again getting a closed surface of genus greater than or equal to \( g \). It follows that our splitting \( S_{s,t} \) has genus equal to at least \( 2g \).
The bulk of this paper is devoted to delicate geometrical arguments. For example, the surfaces \( S_{s,t} \) need to be deformed to a family of harmonic or energy minimizing maps which may result in 2-chains (not necessarily embedded) which still allow the homological minimizing arguments above.
The paper introduces a new technique in its use of harmonic maps to understand the topology of 3-manifolds. This is reminiscent of the important role played by minimal surfaces and seems promising for future applications.