Celebratio Mathematica

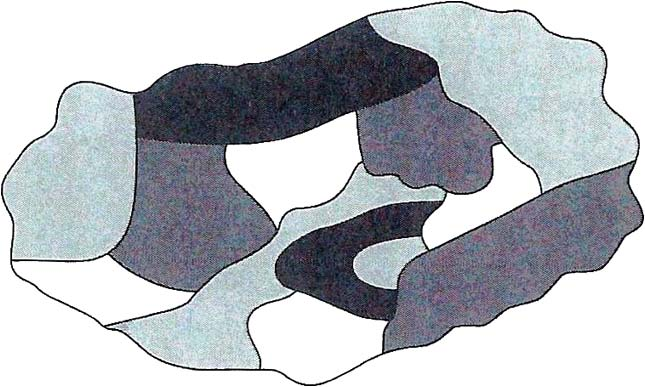
No pro­gress was made on its solu­tion un­til 1878, when Ar­thur Cay­ley posed the ques­tion again at a meet­ing of the Lon­don Math­em­at­ic­al So­ci­ety. In a short note for the Roy­al Geo­graph­ic­al So­ci­ety [e2], he sub­sequently gave a simple ar­gu­ment to show that when try­ing to prove that four col­ors are al­ways enough it is suf­fi­cient to con­sider cu­bic maps — those in which ex­actly three coun­tries (and there­fore three bound­ary lines) meet at each point of in­ter­sec­tion. In what fol­lows, we shall usu­ally as­sume that the maps un­der con­sid­er­a­tion are cu­bic maps, and our ap­proach will be to ex­plain why a min­im­al counter­example — a cu­bic map with the smal­lest pos­sible num­ber of coun­tries that can­not be colored with four col­ors — can­not ex­ist.

In the fol­low­ing year, Al­fred Kempe (a bar­ris­ter and former stu­dent of Cay­ley) answered Gu­thrie’s ques­tion in the af­firm­at­ive. His pa­per “On the geo­graph­ic­al prob­lem of the four col­ours” [e1] ap­peared in the newly foun­ded Amer­ic­an Journ­al of Math­em­at­ics and was com­mis­sioned from him by Cay­ley’s friend J. J. Sylvester. Al­though Kempe’s “solu­tion” was in­cor­rect, it con­tained a num­ber of im­port­ant ideas that re­sur­faced in later at­tempts on the prob­lem, in­clud­ing the even­tu­al proof by Ap­pel and Haken.

First, us­ing Euler’s poly­hed­ron for­mula for maps, \[ (\text{number of countries}) + (\text{number of meeting points}) = (\text{number of boundary edges}) + 2, \]

Kempe proved that every cu­bic map must con­tain at least one coun­try bounded by not more than five edges — a di­gon, tri­angle, quad­ri­lat­er­al, or pentagon, as il­lus­trated in Fig­ure 2. We call any such set an un­avoid­able set of con­fig­ur­a­tions — every cu­bic map must con­tain at least one of them.

Kempe also proved by math­em­at­ic­al in­duc­tion that any map con­tain­ing a di­gon or tri­angle can be colored with four col­ors. For, if the re­mainder of the map is colored with four col­ors, then this col­or­ing can im­me­di­ately be ex­ten­ded to the di­gon or tri­angle, since the coun­tries sur­round­ing it re­quire at most three col­ors. He then ex­ten­ded this idea to maps that con­tain a quad­ri­lat­er­al — here the four coun­tries sur­round­ing it may all be dif­fer­ent, but Kempe showed that we can al­ways in­ter­change pairs of col­ors in the map so that a col­or be­comes avail­able for the quad­ri­lat­er­al. Such an in­ter­change of col­ors is now called a Kempe-in­ter­change.

A re­du­cible con­fig­ur­a­tion of coun­tries in a map is a col­lec­tion of coun­tries with the prop­erty that any col­or­ing of the rest of the map can be ex­ten­ded to these coun­tries, either dir­ectly or after a suc­ces­sion of Kempe-in­ter­changes of col­or; thus, a di­gon, a tri­angle, and a quad­ri­lat­er­al are all re­du­cible con­fig­ur­a­tions. Note that no re­du­cible con­fig­ur­a­tions can ap­pear in a min­im­al counter­example to the four-col­or the­or­em.

Where Kempe ran in­to dif­fi­culties was in try­ing to show that a pentagon is re­du­cible. To do so, he car­ried out two in­ter­changes of col­or for the coun­tries sur­round­ing the pentagon, so that a col­or then be­came avail­able for the pentagon. Since this dealt with every case, he be­lieved that he had com­pleted the proof.

In 1890, P. J. Heawood [e3] showed that car­ry­ing out two such sim­ul­tan­eous in­ter­changes of col­or is in­val­id in gen­er­al, so that Kempe’s proof con­tained a fatal flaw. But Heawood was able to sal­vage enough from Kempe’s ar­gu­ment to prove that every map can be colored with five col­ors — it­self a worth­while res­ult.

For fu­ture ref­er­ence, we note that:

To prove the four-col­or the­or­em, it is enough to find an un­avoid­able set of re­du­cible con­fig­ur­a­tions.

This is be­cause every map must con­tain at least one of these con­fig­ur­a­tions, but each is re­du­cible and so can­not ap­pear in a min­im­al counter­example.

The next ad­vance took place in 1904 when Paul Wer­nicke, an Amer­ic­an math­em­atician study­ing for his doc­tor­ate in Göttin­gen, pro­duced a new un­avoid­able set [e4]. Since the pentagon had not been proved to be re­du­cible, he re­placed it by two oth­er con­fig­ur­a­tions (see Fig­ure 3), hop­ing that these new ones would turn out to be re­du­cible — spe­cific­ally, he proved that any cu­bic map with no di­gon, tri­angle, or quad­ri­lat­er­al must con­tain two ad­ja­cent pentagons or a pentagon ad­ja­cent to a hexagon. We prove this later in this art­icle.

Later, in 1922, Philip Frank­lin of Prin­ceton Uni­versity (and later M.I.T.) ex­ten­ded this res­ult by prov­ing that any cu­bic map with no di­gon, tri­angle, or quad­ri­lat­er­al must con­tain a pentagon ad­ja­cent to two oth­er pentagons, a pentagon and a hexagon, or two hexagons [e6]. Fur­ther un­avoid­able sets were dis­covered by Henri Le­besgue (of Le­besgue in­teg­ral fame) in 1940 [e7].

Mean­while, pro­gress was be­ing made on re­du­cible con­fig­ur­a­tions. Up to now it was known that di­gons, tri­angles, and quad­ri­lat­er­als were re­du­cible, but little fur­ther pro­gress had been made. This situ­ation changed dra­mat­ic­ally in 1913 with the pub­lic­a­tion of a ground-break­ing pa­per by G. D. Birk­hoff, one of the out­stand­ing Amer­ic­an schol­ars of the early 20th cen­tury who made sub­stan­tial con­tri­bu­tions to many areas of math­em­at­ics. Birk­hoff re­garded solv­ing the four-col­or prob­lem as one of his greatest as­pir­a­tions, even though he later re­gret­ted the time he had spent on it.

Birk­hoff pa­per on “The re­du­cib­il­ity of maps” [e5] ap­peared in the Amer­ic­an Journ­al of Math­em­at­ics, where Kempe had pub­lished his “solu­tion” over thirty years earli­er. In this pa­per Birk­hoff gave a sys­tem­at­ic treat­ment of re­du­cible con­fig­ur­a­tions and laid the ground­work for all later de­vel­op­ments in this dir­ec­tion. In par­tic­u­lar, he showed that a par­tic­u­lar con­fig­ur­a­tion, the so-called Birk­hoff dia­mond of four pentagons (shown in Fig­ure 4), is re­du­cible; this im­port­ant con­fig­ur­a­tion was once de­scribed as en­joy­ing as much renown in graph the­ory as the Ko­hinoor dia­mond does in fic­tion­al crim­in­al mys­ter­ies.

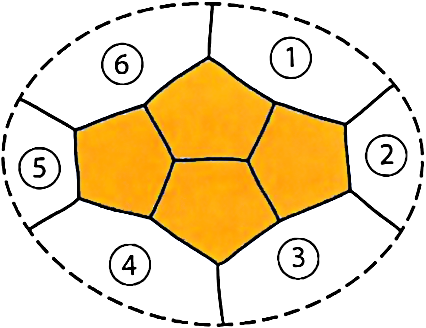
To prove that the Birk­hoff dia­mond is re­du­cible, we sup­pose that we have a min­im­al counter­example that con­tains it. Re­mov­ing the dia­mond yields a new map with few­er coun­tries which can be colored with four col­ors. We now try to ex­tend this col­or­ing to the pentagons in the dia­mond.

To do so, we look at all the pos­sible ways of col­or­ing the ring of six coun­tries sur­round­ing the dia­mond with the col­ors red (r), blue (b), green (g), and yel­low (y). It turns out that there are es­sen­tially thirty-one dif­fer­ent col­or­ings of the coun­tries 1 to 6, six­teen of which (such as rgrbrg) can be ex­ten­ded dir­ectly to the coun­tries of the dia­mond — these are called good col­or­ings — while all the oth­ers (such as rgbrgy) can be con­ver­ted in­to good col­or­ings by suit­able Kempe-in­ter­changes of col­or. Thus, all 31 col­or­ings of the sur­round­ing ring can be ex­ten­ded to the Birk­hoff dia­mond, which is there­fore re­du­cible.

After this the flood-gates were open, and sev­er­al math­em­aticians on both sides of the At­lantic began to de­vel­op Birk­hoff’s ideas, pro­du­cing re­du­cible con­fig­ur­a­tions galore. In par­tic­u­lar, Philip Frank­lin of Prin­ceton proved that each of the fol­low­ing con­fig­ur­a­tions is re­du­cible and so can­not ap­pear in a min­im­al counter­example:

a pentagon in con­tact with three pentagons and a hexagon;
a pentagon sur­roun­ded by two pentagons and three hexagons;
a hexagon sur­roun­ded by four pentagons and two hexagons;
and any \( n \)-sided poly­gon in con­tact with \( n - 1 \) pentagons (such as an oc­ta­gon in con­tact with sev­en pentagons).

By ap­ply­ing a count­ing ar­gu­ment de­rived from Euler’s poly­hed­ron for­mula, he de­duced that every map with up to 25 coun­tries can be colored with four col­ors, and there­fore that a min­im­al counter­example must have at least 26 coun­tries.

Later math­em­aticians con­tin­ued this work, ob­tain­ing fur­ther re­du­cible con­fig­ur­a­tions and us­ing count­ing ar­gu­ments to prove the four-col­or the­or­em for maps with more coun­tries. By the middle of the 20th cen­tury it was known that all maps with up to 35 coun­tries can be colored with four col­ors — but there was still a long way to go.

But much of this work on the four-col­or prob­lem was still piece­meal. At­tempts to find un­avoid­able sets and re­du­cible con­fig­ur­a­tions were largely in­de­pend­ent of each oth­er, and a co­ordin­ated search for the holy grail — an un­avoid­able set of re­du­cible con­fig­ur­a­tions — had not been forth­com­ing. The cred­it for ad­voc­at­ing such a search be­longs to Hein­rich Heesch, whose con­tri­bu­tions would pave the way for the even­tu­al solu­tion of the prob­lem by Ap­pel and Haken in the 1970s.

Heesch’s early ca­reer in math­em­at­ics was spec­tac­u­lar. After ob­tain­ing a doc­tor­ate in math­em­at­ics from the Uni­versity of Zürich for a dis­ser­ta­tion on sym­metry in three-di­men­sion­al geo­metry, he pro­ceeded to Göttin­gen, the home of such dis­tin­guished math­em­aticians as Dav­id Hil­bert, Richard Cour­ant, and Her­mann Weyl, and be­came as­sist­ant to Weyl, study­ing the geo­metry of crys­tals. While in Göttin­gen, Heesch came across the 23 cel­eb­rated “Hil­bert prob­lems” posed by Hil­bert at the In­ter­na­tion­al Con­gress of Math­em­aticians in Par­is in 1900. The four-col­or prob­lem was not one of these, but the “reg­u­lar par­quet prob­lem”, in­volving tilings of the plane, was part of Hil­bert’s Prob­lem 18. Heesch solved this prob­lem in 1932 by con­struct­ing tilings that cov­er the plane ac­cord­ing to the rules laid down in the prob­lem.

The mid-1930s were dif­fi­cult years for Heesch, as for many oth­er Ger­man math­em­aticians. Ob­ject­ing to the Nazi work camps set up for those de­sir­ing to be pro­fess­ors, he soon found him­self without uni­versity em­ploy­ment. For twenty years he taught math­em­at­ics and mu­sic in vari­ous schools and worked on in­dus­tri­al prob­lems that in­volved tiling pat­terns, while con­tinu­ing with his math­em­at­ic­al re­searches. He even­tu­ally se­cured a teach­ing po­s­i­tion at the Tech­nic­al Uni­versity of Han­over.

Heesch’s in­terest in the four-col­or prob­lem dates from around 1935. His friend Ernst Witt be­lieved that he had found a proof and they went to show this to Cour­ant. But Cour­ant was about to em­bark on a train jour­ney to Ber­lin, so Heesch and Witt bought train tick­ets too and ac­com­pan­ied him on his jour­ney. Fail­ing to con­vince Cour­ant that the proof was cor­rect they caught the train back to Göttin­gen: on the re­turn jour­ney, Heesch found an er­ror in Witt’s proof.

Un­avoid­able sets were still rather scarce, and in or­der to pro­duce them Heesch in­ven­ted his meth­od of dis­char­ging, first pub­lished in 1969; the term dis­char­ging is due to Haken. The gen­er­al ap­proach is as fol­lows. To prove that a giv­en set of con­fig­ur­a­tions is an un­avoid­able set, we as­sume the op­pos­ite — that there is a cu­bic map con­tain­ing none of them. We next as­sign to each coun­try a num­ber — like an elec­tric­al charge — so that the total charge on the coun­tries of the map is pos­it­ive. We then try to move these charges around the map in such a way that no charge is cre­ated or des­troyed, and so that each in­di­vidu­al coun­try ends up with zero or neg­at­ive charge (this is called dis­char­ging the map). Then the total charge on the map can­not be pos­it­ive. This con­tra­dic­tion proves that the giv­en set of con­fig­ur­a­tions is an un­avoid­able set.

To il­lus­trate the meth­od of dis­char­ging we prove Wer­nicke’s res­ult that the con­fig­ur­a­tions in Fig­ure 3 form an un­avoid­able set, and to do so we as­sume that we have a cu­bic map that con­tains none of them and ob­tain a con­tra­dic­tion. Our as­sump­tion tells us that no pentagon can be ad­ja­cent to a di­gon, tri­angle, or quad­ri­lat­er­al, or to an­oth­er pentagon or a hexagon, so each pentagon can ad­join only coun­tries bounded by sev­en edges or more.

We now as­sign the elec­tric­al charges. To each coun­try with k bound­ary lines, we as­sign a charge of \( 6 - k \), so that each pentagon (\( k = 5 \)) re­ceives a charge of 1, each hexagon (\( k = 6 \)) re­ceives zero charge, each hep­tagon (\( k = 7 \)) re­ceives a charge of \( -1 \), and so on. So if the map has \( C_5 \) pentagons, \( C_6 \) hexagons, \( C_7 \) hep­tagons, etc., then the total charge on the map is \begin{multline*} \tag{*} (1 \times C_5 ) + (0 \times C_6 ) + (-1 \times C_7 ) + (-2 \times C_8 )\\ + (-3 \times C_9 ) + (-4 \times C_10 ) + \cdots\\ = C_5 - C_7 - 2C_8 - 3C_9 - 4C_{10} - \cdots. \end{multline*}

But one can eas­ily prove from Euler’s poly­hed­ron for­mula that, for a cu­bic map with \( C_2 \) di­gons, \( C_3 \) tri­angles, \( C_4 \) squares, etc., \[ 4C_{2} + 3C_3 + 2C_4 + C_5 - C_7 - 2C_8 - 3C_9 - 4C_{10} - \cdots = 12, \] and so, since our map has no di­gons, tri­angles, or quad­ri­lat­er­als (\( C_2 = C_3 = C_4 = 0 \)), \[ \tag{*} C_5 - C_7 - 2C_8 - 3C_9 - 4C_{10} - \cdots = 12. \]

Com­par­ing the two starred res­ults, we see that the total charge on the map is 12, which is pos­it­ive.

We now move the charges around the map, trans­fer­ring one-fifth of a unit of charge from each pentagon to each of its five neg­at­ively charged neigh­bors: re­call that each of these neigh­bors has sev­en or more sides. Then the total charge on the map re­mains 12, but each pentagon now has zero charge and each hexagon still has zero charge.

What hap­pens to a hep­tagon? If a hep­tagon with ini­tial charge \( -1 \) re­ceives enough con­tri­bu­tions of \( \tfrac{1}{5} \) to ac­quire pos­it­ive charge, then it must have at least 5 six neigh­bor­ing pentagons — but two of these pentagons would then have to be ad­ja­cent, which is dis­al­lowed; thus, after the dis­char­ging, each hep­tagon re­tains neg­at­ive charge. In the same way we can prove that each oc­ta­gon, non­agon, deca­gon, etc., re­tains neg­at­ive charge.

Thus, each coun­try ends up with zero or neg­at­ive charge, con­tra­dict­ing our as­ser­tion that the total charge on the map is 12. This con­tra­dic­tion proves that every cu­bic map must con­tain at least one of Wer­nicke’s con­fig­ur­a­tions of coun­tries, which there­fore form an un­avoid­able set.

By modi­fy­ing the above meth­od of dis­char­ging we can show that many sets of con­fig­ur­a­tions are un­avoid­able, but the de­tails of the dis­char­ging pro­cess will vary from situ­ation to situ­ation: in oth­er cases it may be more ad­vant­age­ous to trans­fer one-fourth or one-third of a unit, or to dis­trib­ute the charge on each pentagon equally to all of its neigh­bors (as we see later). As the cen­tury pro­gressed, un­avoid­able sets with thou­sands of con­fig­ur­a­tions were con­struc­ted. To deal with such enorm­ous sets it proved ne­ces­sary to keep on modi­fy­ing the dis­char­ging pro­cess un­til it could deal with every pos­sible case that arose.

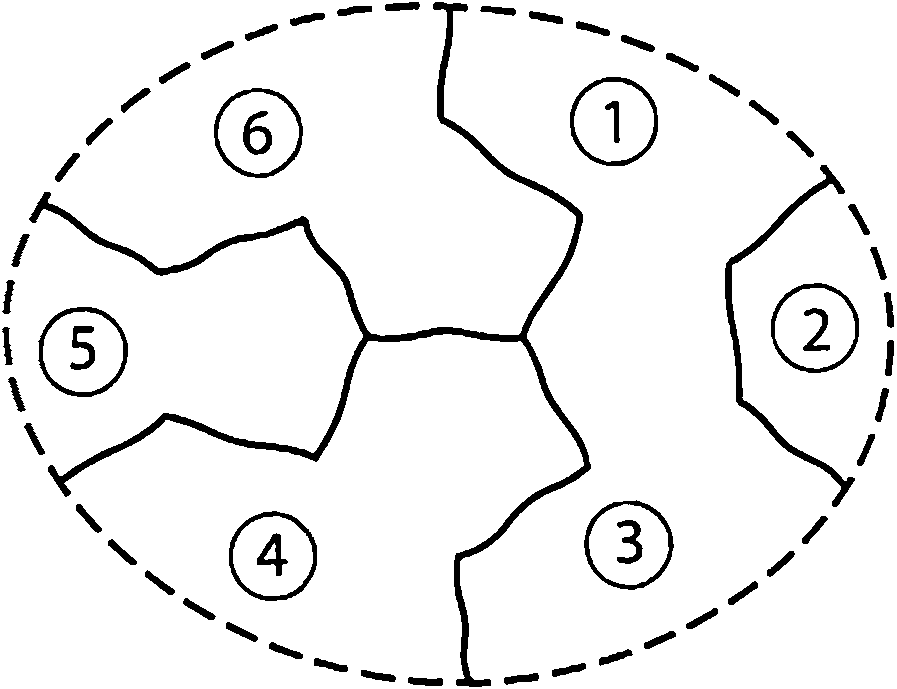
Heesch also con­trib­uted to the the­ory of re­du­cible con­fig­ur­a­tions, ob­tain­ing many thou­sands of them. When dis­cuss­ing the Birk­hoff dia­mond, we saw that all thirty-one pos­sible col­or­ings of the ring of coun­tries sur­round­ing the dia­mond are all good col­or­ings, or can be con­ver­ted to good col­or­ings by a suc­ces­sion of Kempe col­or-in­ter­changes. Heesch in­tro­duced the term \( D \)-re­du­cible for such con­fig­ur­a­tions of coun­tries.

In fact, we do not have to con­sider all thirty-one col­or­ings. If we modi­fy the map by re­mov­ing five of the bound­ary lines, as shown in Fig­ure 5, then we ob­tain a new map with few­er coun­tries which can there­fore be colored with four col­ors. Heesch used the term \( C \)-re­du­cible for those con­fig­ur­a­tions that can be proved re­du­cible after they have been mod­i­fied in some way. The con­cepts of \( D \)-re­du­cible and \( C \)-re­du­cible con­fig­ur­a­tion will fea­ture again later.

In the late 1940s Heesch presen­ted his find­ings pub­licly for the first time at the Uni­versit­ies of Ham­burg and his home town of Kiel. He had in­creas­ingly come to be­lieve that the right ap­proach to the four-col­or prob­lem was to seek an un­avoid­able set of re­du­cible con­fig­ur­a­tions. In his lec­tures Heesch ex­pounded on his be­lief that there ex­is­ted such a set and that its con­fig­ur­a­tions would not be par­tic­u­larly large, but that there would be a great num­ber of them.

One stu­dent who at­ten­ded Heesch’s 1948 lec­tures at the Uni­versity of Kiel was the young Wolfgang Haken, who had entered the Uni­versity as its young­est stu­dent and was study­ing math­em­at­ics, philo­sophy, and phys­ics. Haken still re­calls hear­ing Heesch’s lec­ture, much of which he did not un­der­stand at the time, but re­mem­bers Heesch men­tion­ing that there might be some ten thou­sand cases to be in­vest­ig­ated, that five hun­dred con­fig­ur­a­tions had already been checked at an av­er­age rate of about one per day, and that he seemed op­tim­ist­ic about deal­ing with the re­main­ing nine-and-a-half thou­sand cases.

Among the most stim­u­lat­ing series of lec­tures that Haken at­ten­ded at Kiel were those on to­po­logy by the only math­em­at­ics pro­fess­or, Karl Weise, who had him­self worked on the four-col­or prob­lem. In these lec­tures Weise de­scribed three long-stand­ing prob­lems that re­mained un­solved at that time: the knot prob­lem (de­term­in­ing wheth­er a giv­en tangle of string in three di­men­sions con­tains a knot), the now-solved Poin­caré con­jec­ture (con­cern­ing spheres in four-di­men­sion­al space), and the four-col­or prob­lem. Haken was to be­come fully in­volved with all three prob­lems, in each case us­ing “very ele­ment­ary means on which every­one else had giv­en up”. The first prob­lem he solved com­pletely — a great achieve­ment — and an­nounced his res­ults at the 1954 In­ter­na­tion­al Con­gress of Math­em­aticians in Am­s­ter­dam. The second he at­tacked vig­or­ously, re­du­cing it to 200 par­tic­u­lar cases, 198 of which he sys­tem­at­ic­ally and suc­cess­fully man­aged to deal with, but (frus­trat­ingly) not the fi­nal two. The third he battled with for sev­er­al years, as we shall see.

Haken’s work on the knot prob­lem so im­pressed Bill Boone, a lo­gi­cian at the Uni­versity of Illinois at Urb­ana-Cham­paign, that Haken was in­vited to Illinois as a vis­it­ing pro­fess­or. Shortly after ar­riv­ing there, he gave sev­er­al lec­tures on his re­searches in­to the knot prob­lem. His painstak­ing ap­proach to solv­ing math­em­at­ic­al prob­lems stim­u­lated one of his col­leagues to ob­serve:

Math­em­aticians usu­ally know when they have got­ten too deep in­to the forest to pro­ceed any fur­ther. That is the time Haken takes out his pen­knife and cuts down the trees one at a time.

The 1960s proved to be an ex­cit­ing time for map col­or­ing. In 1967 the first ma­jor book de­voted ex­clus­ively to map col­or­ing, Oystein Ore’s au­thor­it­at­ive and in­flu­en­tial The Four-Col­or Prob­lem [e9], was pub­lished, and in 1968 Ore and his re­search stu­dent Joel Stemple ex­ten­ded the earli­er meth­ods of Frank­lin and oth­ers to prove that all maps with up to 40 coun­tries can be colored with four col­ors: their proof in­volved the con­sid­er­a­tion of so many spe­cial cases that the full de­tails could not be pub­lished, but had to be de­pos­ited with the Math­em­at­ics De­part­ment Lib­rary at Yale Uni­versity.

In 1967 Haken con­tac­ted Heesch. With his ex­per­i­ence of the Poin­caré prob­lem, in which just two out of two hun­dred cases had failed to work, Haken feared that the same thing might have happened to Heesch with his ten thou­sand con­fig­ur­a­tions, and that Heesch might have giv­en up — but no: Heesch was still work­ing on the prob­lem. By this time, Heesch had in­ven­ted the meth­od of dis­char­ging and had dis­covered thou­sands of re­du­cible con­fig­ur­a­tions. But al­though he lec­tured widely about his work, it re­mained un­pub­lished un­til 1969 when he pro­duced a pa­per­back in Ger­man con­tain­ing the meth­od of dis­char­ging and his many oth­er con­tri­bu­tions.

Heesch’s aim was to “sys­tem­at­ize” the ideas in Birk­hoff’s 1913 pa­per by de­vel­op­ing an ap­proach for gen­er­at­ing re­du­cible con­fig­ur­a­tions, look­ing at both \( D \)-re­du­cible and \( C \)-re­du­cible ones. If a con­fig­ur­a­tion was not \( D \)-re­du­cible, Heesch could fre­quently see how to modi­fy it so as to de­term­ine wheth­er it was \( C \)-re­du­cible. By this means he could re­strict his at­ten­tion to a smal­ler num­ber of pos­sible col­or­ings, as happened for the Birk­hoff dia­mond.

Over the years Heesch had de­veloped an un­canny knack of be­ing able to look at a con­fig­ur­a­tion and say­ing wheth­er it was re­du­cible, with at least 80 per cent ac­cur­acy. As Haken re­marked:

What fas­cin­ated me most was that Heesch looked at the con­fig­ur­a­tion, and he either said, “No, there is no chance. That can­not be re­du­cible”, or he said, “But this one: that is cer­tainly re­du­cible”.

Haken in­vited Heesch to the Uni­versity of Illinois to give a lec­ture, and raised the ques­tion of wheth­er com­puters might be help­ful in the ex­am­in­a­tion of large num­bers of con­fig­ur­a­tions. Heesch had already had the same idea, and in the mid-1960s had ob­tained the help of Karl Dürre, a math­em­at­ics gradu­ate from Han­over who had be­come a school­teach­er. Dürre de­veloped u a meth­od for test­ing \( D \)-re­du­cib­il­ity that was suf­fi­ciently routine and al­gorithmic to be im­ple­men­ted on a com­puter, even though it might take a long time. By Novem­ber 1965, us­ing Al­gol 60 on the Uni­versity of Han­over’s CDC 1604A com­puter, Dürre con­firmed that the Birk­hoff dia­mond is \( D \)-re­du­cible u and as­cer­tained the \( D \)-re­du­cib­il­ity of many more con­fig­ur­a­tions of in­creas­ing com­plex­ity.

The com­plex­ity of a con­fig­ur­a­tion can be meas­ured by its ring-size, the num­ber of coun­tries sur­round­ing the con­fig­ur­a­tion. As we saw earli­er, the Birk­hoff dia­mond has ring-size 6, and there are 31 es­sen­tially dif­fer­ent col­or­ings of the coun­tries sur­round­ing it. Un­for­tu­nately, the num­ber of dif­fer­ent col­or­ings in­creases rap­idly as the ring-size in­creases, as we can see from the fol­low­ing table: \[ \begin{array}{lrrrrrrrrr} \hline \text{Ring-size} &6 &7 &8 &9 &10 &11 &12 &13 &14\\ \text{Colorings} &31 &91 &274 &820 &2461 &7381 &22144 &64430 &199291\\ \hline \end{array} \] So, for a con­fig­ur­a­tion of eight coun­tries with ring-size 14, we have al­most two hun­dred thou­sand es­sen­tially dif­fer­ent col­or­ings to con­sider. Moreover, in­form­al cal­cu­la­tions first in­dic­ated that a solu­tion to the four-col­or prob­lem might in­volve con­fig­ur­a­tions with ring-size 18, where the num­ber of col­or­ings ex­ceeds 16 mil­lion.

Heesch and Dürre found that the time taken to ana­lyze a con­fig­ur­a­tion u in­creases rap­idly as its ring-size in­creases. On their ma­chine a typ­ic­al con­fig­ur­a­tion with ring-size 12 might take six hours to ana­lyze, while some con­fig­ur­a­tions with ring-size 13 took any­thing between 16 and 61 hours, and those of ring-size 14 were bey­ond reach. They es­tim­ated that to veri­fy all ten thou­sand cases might in­volve up to fifty thou­sand hours of com­puter time; this was not a real­ist­ic pro­pos­i­tion on any com­puter then avail­able.

By this time it was clear that any solu­tion of the four-col­or prob­lem along these lines would have to be com­plic­ated. In the 1960s E. F. Moore of the Uni­versity of Wis­con­sin de­veloped a re­mark­able knack for con­struct­ing maps that con­tain no known re­du­cible con­fig­ur­a­tions; he thereby hoped to find a map that re­quired five col­ors. One of his maps con­tained no re­du­cible con­fig­ur­a­tions with ring-size 11 or less, so any un­avoid­able set of re­du­cible con­fig­ur­a­tions ne­ces­sar­ily con­tains at least one re­du­cible con­fig­ur­a­tion of ring-size 12 or great­er (see [e12]).

Al­though it looked as though con­fig­ur­a­tions of ring-size up to 18 might be ne­ces­sary, in the event the Ap­pel–Haken solu­tion in­volved only con­fig­ur­a­tions with ring-size 14 and less. Had it re­quired any lar­ger con­fig­ur­a­tions they would al­most cer­tainly not have been able to com­plete their solu­tion when they did.

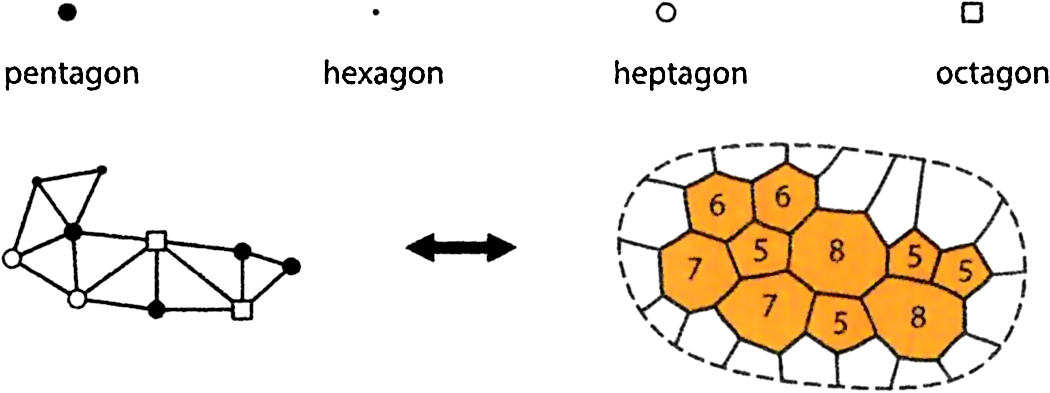
By this time, most work­ers on the four-col­or prob­lem were us­ing the “dual for­mu­la­tion”, in­tro­duced by Kempe, of col­or­ing the points of the cor­res­pond­ing graph or link­age. In par­tic­u­lar, Heesch de­vised a use­ful nota­tion, which soon be­came widely used, for rep­res­ent­ing each point by an ap­pro­pri­ate “blob” so that it can be eas­ily dis­tin­guished. Four of Heesch’s sym­bols and an ex­ample are shown in Fig­ure 6.

It soon be­came clear that the Han­over com­puter was in­suf­fi­ciently power­ful to carry out the work re­quired of it. Haken tried to help Heesch and Dürre by bid­ding to the Uni­versity of Illinois for time on a new su­per­com­puter whose con­struc­tion was near­ing com­ple­tion, but it was not yet ready for use. Even­tu­ally, they were re­ferred to Heesch’s friend Yosh­io Shi­m­amoto, Dir­ect­or of the Com­puter Centre at the Atom­ic En­ergy Com­mis­sion’s Brookhaven labor­at­ory in Up­ton, Long Is­land, where there was a Cray Con­trol Data 6600 ma­chine, the most power­ful ma­chine of its day.

Shi­m­amoto had al­ways been an en­thu­si­ast for the four-col­or prob­lem and was strongly sup­port­ive of Heesch’s ap­proach to the prob­lem. He gen­er­ously in­vited Heesch and Dürre to vis­it Brookhaven and con­tin­ue their re­du­cib­il­ity test­ing on the Cray com­puter (see Fig­ure 7). Heesch paid two ex­ten­ded vis­its, in­clud­ing a stay of one year, while Dürre vis­ited for al­most two years.

At Brookhaven pro­gress was quickly made. A con­fig­ur­a­tion with ring-size 13 was not ex­cess­ively large for the Cray com­puter, and those with ring-size 14 could be tested for the first time. Even­tu­ally, Heesch and Dürre were able to con­firm the \( D \)-re­du­cib­il­ity of more than a thou­sand con­fig­ur­a­tions.

Mean­while, Shi­m­amoto was car­ry­ing on his own re­searches in­to the prob­lem. Un­likely as it may seem, he showed that if he could find a single con­fig­ur­a­tion with cer­tain par­tic­u­lar prop­er­ties, and if this con­fig­ur­a­tion were \( D \)-re­du­cible, then the four-col­or the­or­em would fol­low: the whole of the proof would de­pend on a single con­fig­ur­a­tion! Sud­denly, on 30 Septem­ber 1971, he found what he was seek­ing, a con­fig­ur­a­tion with ring-size 14 that be­come known as the Shi­m­amoto horse­shoe (see Fig­ure 8): if this horse­shoe were \( D \)-re­du­cible, then the four-col­or prob­lem would be solved.

Co­in­cid­ent­ally Heesch and Haken were vis­it­ing Brookhaven on that very day. Heesch re­cog­nized the horse­shoe as one of his list of \( D \)-re­du­cible con­fig­ur­a­tions, but Shi­m­amoto was cau­tious and asked for it to be rechecked for \( D \)-re­du­cib­il­ity. Ex­cite­ment ran ri­ot: ru­mors about Shi­m­amoto’s solu­tion were be­gin­ning to en­circle the world. On the day fol­low­ing the horse­shoe’s dis­cov­ery, Haken was due to vis­it the Prin­ceton In­sti­tute for Ad­vanced Study be­fore re­turn­ing to Illinois, and he asked Shi­m­amoto’s per­mis­sion to tell people about the res­ult. Ac­cord­ing to Haken, Shi­m­amoto said “yes”, while Shi­m­amoto later denied do­ing so and be­came some­what an­noyed about Haken’s pro­nounce­ment, com­plain­ing that:

I am get­ting a de­luge of ques­tions from many people and I am now won­der­ing about the wis­dom of hav­ing you talk at Prin­ceton and Urb­ana be­fore a clean manuscript had been pre­pared.

In the event, things did not work out as hoped. The su­per­fast Cray com­puter was al­lowed to run for a whole week­end, and after grind­ing on for twenty-six ex­cru­ci­at­ing hours, it con­firmed that the horse­shoe was not \( D \)-re­du­cible after all. There was great dis­ap­point­ment all round.

It seemed as though the four-col­or prob­lem had again come to a dead end. But Heesch’s ap­proach was be­gin­ning to pay di­vidends, and in the hands of Haken and Ap­pel would yield the de­sired goal with­in the next five years.

In 1970 Heesch sent Haken the res­ults of a new dis­char­ging ex­per­i­ment, in which the pos­it­ive charge on each pentagon was now to be dis­trib­uted equally to all neigh­bor­ing coun­tries with neg­at­ive charge. The res­ult of this ex­per­i­ment, if ap­plied to a gen­er­al map, would yield about 8900 “bad” con­fig­ur­a­tions ex­tend­ing up to ring-size 18, in which some coun­tries would still have pos­it­ive charge. This ap­proach, the fi­nit­iz­a­tion of the four-col­or prob­lem, re­duced the prob­lem to the con­sid­er­a­tion of these 8900 con­fig­ur­a­tions, which Heesch pro­posed to work through one at a time.

Haken, however, was highly pess­im­ist­ic about be­ing able to deal with such a large num­ber of con­fig­ur­a­tions, es­pe­cially since some of them were fairly large. By this time, it had be­come a simple mat­ter to test con­fig­ur­a­tions of ring-size 11, since there are only 7381 dif­fer­ent col­or­ings of the sur­round­ing ring of el­ev­en coun­tries, but each time the ring-size in­creased by 1 the cor­res­pond­ing com­puter time seemed to ex­pand by a factor of four, with a cor­res­pond­ing in­crease in stor­age. Re­call­ing that the dif­fi­cult horse­shoe con­fig­ur­a­tion with ring-size 14 had taken twenty-six hours to run, Ap­pel and Haken later ob­served:

Even if the av­er­age time re­quired for ex­amin­ing four­teen-ring con­fig­ur­a­tions was only 25 minutes, the factor of four to the fourth power in passing from four­teen- to eight­een-rings would im­ply that the av­er­age eight­een-ring con­fig­ur­a­tion would re­quire over 100 hours of time and much more stor­age than was avail­able on any ex­ist­ing com­puter. If there were a thou­sand con­fig­ur­a­tions of ring-size 18, then the whole pro­cess would take over 100,000 hours, or about el­ev­en years, on a fast com­puter.

For some time, Haken had felt that the com­plex­ity of the prob­lem would be sub­stan­tially sim­pli­fied if one could find a bet­ter dis­char­ging meth­od. By re­strict­ing his at­ten­tion to maps without hexagons or hep­tagons, he suc­ceeded in find­ing a much sim­pler pro­ced­ure. En­cour­aged by this, he then pro­ceeded to gen­er­al maps, and com­mu­nic­ated his find­ings to Heesch.

Im­pressed by these, Heesch in­vited Haken to col­lab­or­ate with him, and in 1971 sent him sev­er­al of his un­pub­lished res­ults con­cern­ing re­du­cible con­fig­ur­a­tions. These in­cluded three “obstacles to re­du­cib­il­ity” whose pres­ence seemed to pre­vent a con­fig­ur­a­tion from be­ing re­du­cible. Al­though it has nev­er been proved that a con­fig­ur­a­tion con­tain­ing one of them can­not be re­du­cible, no such re­du­cible con­fig­ur­a­tion has ever been found, and so it seemed sens­ible to ex­clude them from con­sid­er­a­tion. The three obstacles are shown in Fig­ure 9: a 4-leg­ger coun­try ad­join­ing four con­sec­ut­ive coun­tries of the sur­round­ing ring, a 3-leg­ger ar­tic­u­la­tion coun­try ad­join­ing three sur­round­ing coun­tries that are not all ad­ja­cent, and a hanging 5–5 pair of ad­ja­cent pentagons that ad­join a single coun­try in­side the sur­round­ing ring.

But by this time, Haken was be­gin­ning to change his ap­proach to the prob­lem. Un­like every­one else whose ob­ject­ive seemed to be to col­lect re­du­cible con­fig­ur­a­tions by the hun­dreds and then pack­age them up in­to an un­avoid­able set, Haken’s primary mo­tiv­a­tion, later de­veloped with Ap­pel, was to aim dir­ectly for an un­avoid­able set. In or­der to avoid wast­ing time check­ing con­fig­ur­a­tions that would even­tu­ally be of no in­terest, this set was to con­tain only con­fig­ur­a­tions that were likely to be re­du­cible — in par­tic­u­lar, they should con­tain none of the re­duc­tion obstacles. Any con­fig­ur­a­tions that sub­sequently proved not to be re­du­cible could then be dealt with in­di­vidu­ally. Haken also con­sidered it in­ap­pro­pri­ate to spend ex­pens­ive com­puter time check­ing the re­du­cib­il­ity of con­fig­ur­a­tions that were un­likely to ap­pear in the even­tu­al un­avoid­able set. As he later com­men­ted:

If you want to im­prove something, you should not im­prove that part which is already in good shape. The weak­est point is al­ways the one you should im­prove. This is a very simple an­swer to why we got it and not the oth­ers.

So from this point on, Haken headed off in a dif­fer­ent dir­ec­tion from every­one else, con­cen­trat­ing on the un­avoid­able set and leav­ing de­tails of the re­du­cib­il­ity un­til much later. Heesch, while ini­tially sym­path­et­ic to these ideas, came to re­ject the idea of a “likely-to-be-re­du­cible” con­fig­ur­a­tion, and their co­oper­a­tion was doubt­less fur­ther dam­aged by the horse­shoe epis­ode. Mean­while, Heesch was hav­ing im­mense prob­lems ob­tain­ing the ne­ces­sary fund­ing for the use of a power­ful com­puter. As a re­l­at­ively minor fig­ure in the aca­dem­ic hier­archy he had little “clout”, and his pro­pos­als for fund­ing did not re­ceive the con­sid­er­a­tion they de­served.

With little know­ledge of com­put­ing and with the Brookhaven ma­chine no longer avail­able, Wolfgang Haken also con­sidered giv­ing up the prob­lem for a few years un­til more power­ful com­puters had be­come avail­able to deal with the massive cal­cu­la­tions that would clearly be ne­ces­sary. Com­puter “ex­perts” had told him that his ideas could not be pro­grammed, and in a lec­ture in Illinois on the horse­shoe epis­ode he an­nounced:

The com­puter ex­perts have told me that it is not pos­sible to go on like that. But right now I’m quit­ting. I con­sider this to be the point to which and not bey­ond one can go without a com­puter.

At­tend­ing his lec­ture was Ken­neth Ap­pel, who had re­ceived his doc­tor­ate from the Uni­versity of Michigan for a dis­ser­ta­tion on the ap­plic­a­tion of math­em­at­ic­al lo­gic to prob­lems in al­gebra. An ex­per­i­enced com­puter pro­gram­mer, he had worked for Douglas Air­craft and for the In­sti­tute for De­fense Ana­lys­is at Prin­ceton be­fore set­tling at the Uni­versity of Illinois. His com­puter ex­per­i­ence would prove in­valu­able for solv­ing the four-col­or prob­lem.

After the lec­ture Ap­pel told Haken that he con­sidered the com­puter ex­perts to be talk­ing non­sense, and offered to work on the prob­lem of im­ple­ment­ing the dis­char­ging pro­ced­ures:

I don’t know of any­thing in­volving com­puters that can’t be done; some things just take longer than oth­ers. Why don’t we take a shot at it?

Co­in­cid­ent­ally, Thomas Os­good, a re­search stu­dent of Haken’s, had just sub­mit­ted his doc­tor­al thes­is on solv­ing the four-col­or prob­lem for maps con­tain­ing only pentagons, hexagons, and oc­ta­gons. Since Ap­pel was a mem­ber of Os­good’s thes­is ex­am­in­a­tion pan­el, the col­lab­or­a­tion seemed be­ne­fi­cial for all con­cerned.

Haken was de­lighted to ac­cept Ap­pel’s of­fer to take care of the com­put­ing side of things. They de­cided to con­cen­trate their search on un­avoid­able sets, without tak­ing time to check the con­fig­ur­a­tions for re­du­cib­il­ity, and fo­cused on geo­graph­ic­ally good con­fig­ur­a­tions that con­tain neither of Heesch’s first two obstacles to re­du­cib­il­ity: such con­fig­ur­a­tions can eas­ily be iden­ti­fied by a com­puter, or in­deed by hand. They would then check their con­fig­ur­a­tions for re­du­cib­il­ity when the en­tire set had been con­struc­ted. But when they star­ted work in late 1972 Haken and Ap­pel had no clear idea of where they were head­ing. As Ap­pel re­called:

We star­ted with cer­tain ideas and kept dis­cov­er­ing that we had to be­come more soph­ist­ic­ated to avoid be­ing swamped by use­less or re­pet­it­ive data.

Their first ex­plor­at­ory com­puter runs already provided much use­ful in­form­a­tion since geo­graph­ic­ally good con­fig­ur­a­tions of reas­on­able size (with ring-size 16 or less) ten­ded to ap­pear close to most coun­tries with ul­ti­mately pos­it­ive charge. Since the com­puter out­put was enorm­ous, with many con­fig­ur­a­tions ap­pear­ing many times, they needed to keep such du­plic­a­tions un­der con­trol if the even­tu­al list were to be man­age­able. For­tu­nately, since the com­puter pro­gram had run in just a few hours, they could ex­per­i­ment as fre­quently as they needed to.

The ne­ces­sary changes to the pro­gram were eas­ily im­ple­men­ted and the second set of runs, a month later, was a def­in­ite im­prove­ment. The out­put was much re­duced in thick­ness, and would even­tu­ally come down to a frac­tion of an inch. The ma­jor prob­lems had been over­come and less­er ones would gradu­ally emerge. From then on, every two weeks or so, they mod­i­fied the dis­char­ging al­gorithm or the com­puter pro­gram so that the pro­gram grew while the out­put shrank. This two-way dia­log with the com­puter con­tin­ued, as prob­lems were sor­ted out and new ones arose. With­in six months of ex­per­i­ment­ing and im­prov­ing their pro­ced­ures, they real­ized that their meth­od for pro­du­cing a fi­nite un­avoid­able set of geo­graph­ic­ally good con­fig­ur­a­tions in a reas­on­able amount of time was in­deed feas­ible.

At this stage they changed tack. They de­cided to prove the­or­et­ic­ally that their meth­od would provide such an un­avoid­able set. This proved to be much more com­plic­ated than they had ex­pec­ted, tak­ing them more than a year to com­plete. But the out­come, in late 1974, was a lengthy proof that an un­avoid­able set of geo­graph­ic­ally good con­fig­ur­a­tions ex­ists, to­geth­er with an achiev­able meth­od for con­struct­ing such a set.

Their next task was to de­term­ine how com­plic­ated this pro­cess would be. They de­cided to ex­per­i­ment with the par­tic­u­lar case of maps that do not con­tain two ad­ja­cent pentagons. This was much sim­pler than the gen­er­al case, and pro­duced a set of 47 geo­graph­ic­ally good re­du­cible con­fig­ur­a­tions of ring-size 16 or less [1], as shown in Fig­ure 10. Based on their ex­per­i­ment, they es­tim­ated that the gen­er­al prob­lem might be about fifty times as bad as this, and on this basis they de­cided to pro­ceed: in the event, their es­tim­ate turned out to be over-op­tim­ist­ic.

In early 1975 they in­tro­duced the third of Heesch’s obstacles, the hanging 5–5 pair. This in­ev­it­ably in­volved changes in pro­ced­ure, but was car­ried out suc­cess­fully with only a doub­ling in the size of the un­avoid­able set. They also pro­grammed the com­puter to search for sets of con­fig­ur­a­tions with re­l­at­ively small ring-size.

At this stage, the com­puter star­ted to think for it­self, as Ap­pel and Haken later re­called:

It would work out com­plex strategies based on all the tricks it had been “taught” and of­ten these ap­proaches were far more clev­er than those we would have tried. Thus it began to teach us things about how to pro­ceed that we nev­er ex­pec­ted. In a sense it had sur­passed its cre­at­ors in some as­pects of the “in­tel­lec­tu­al” as well as the mech­an­ic­al parts of the task.

As soon as it seemed prob­able that they would be able to find an obstacle-free un­avoid­able set of con­fig­ur­a­tions, which were there­fore likely to be re­du­cible, they star­ted the massive de­tailed check for re­du­cib­il­ity. In­ev­it­ably, some “rogue” re­du­cible con­fig­ur­a­tions would ap­pear in the list, but the hope was that they would be re­l­at­ively few in num­ber. Also, with con­fig­ur­a­tions that might go up to ring-size 16, and oth­ers that might cause trouble in oth­er ways, they were ex­pect­ing to have to de­vise some clev­er short cuts.

In the middle of 1974, know­ing that they would need help with the re­du­cib­il­ity pro­grams, Ap­pel asked wheth­er any gradu­ate stu­dent would be in­ter­ested in writ­ing a thes­is in the area of pro­gram­ming, and co­in­cid­ent­ally John Koch was look­ing around for a suit­able top­ic. They set up Koch’s thes­is pro­ject so that its com­ple­tion would not de­pend on the suc­cess of their at­tack on the four-col­or prob­lem.

Koch was set to work on the \( C \)-re­du­cib­il­ity of con­fig­ur­a­tions of ring-size 11. Ap­pel and Haken were par­tic­u­larly in­ter­ested in two types of modi­fic­a­tion that were re­l­at­ively easy to im­ple­ment, and Koch dis­covered that 90 per cent of his con­fig­ur­a­tions were of these types. Agree­ing that little would be gained by in­clud­ing the oth­er ten per cent, which would have been dif­fi­cult to pro­gram, they re­stric­ted their at­ten­tion to the simple modi­fic­a­tions. Koch then de­vised an el­eg­ant and highly ef­fi­cient meth­od for test­ing the \( C \)-re­du­cib­il­ity of these con­fig­ur­a­tions of ring-size 11, which Ap­pel sub­sequently ex­ten­ded to con­fig­ur­a­tions of ring-sizes 12, 13, and 14.

To­wards the end of 1975, their work on the dis­char­ging meth­od had run in­to trouble: struc­tur­al changes would be ne­ces­sary, re­quir­ing sig­ni­fic­ant modi­fic­a­tions to the pro­gram. The prob­lem was that, while try­ing to dis­perse the pos­it­ive charge on each pentagon to its im­me­di­ate neigh­bors, they reg­u­larly came up against “bar­ri­ers of hexagons”, all with zero charge. Haken asked him­self why the pos­it­ive charge on the pentagons should not be per­mit­ted to “jump over” these hexagons. This would give a more ef­fi­cient pro­cess, but would leave them with a di­lemma: should they re­write their pro­gram from scratch or should they ad­opt a more ad hoc ap­proach? Since the former would have been a hor­rendous task, they op­ted for the lat­ter, im­ple­ment­ing the fi­nal ver­sion of the dis­char­ging pro­cess by hand. This in­ev­it­ably in­volved much work, but gave them ex­tra flex­ib­il­ity by en­abling them to make minor changes whenev­er ne­ces­sary. In­deed, they found so many im­prove­ments that they could re­strict all of their con­fig­ur­a­tions to ring-size 14 or less.

Throughout the first half of 1976, Haken and Ap­pel worked on the fi­nal de­tails of the dis­char­ging pro­ced­ure in or­der to pro­duce the de­sired un­avoid­able set of re­du­cible con­fig­ur­a­tions. To do this, they sought out “prob­lem con­fig­ur­a­tions” that would ne­ces­sit­ate fur­ther changes to the dis­char­ging pro­ced­ure. Whenev­er they found such a con­fig­ur­a­tion, they im­me­di­ately tested it for re­du­cib­il­ity — this could usu­ally be done fairly quickly. In this way the re­du­cib­il­ity test­ing by com­puter could keep pace with the manu­al con­struc­tion of the dis­char­ging pro­ced­ure. In the event, the fi­nal pro­cess in­volved 487 dis­char­ging rules, re­quir­ing the in­vest­ig­a­tion by hand of about 10,000 neigh­bor­hoods of coun­tries with pos­it­ive charge and the re­du­cib­il­ity test­ing by com­puter of some 2000 con­fig­ur­a­tions.

Be­cause the re­du­cib­il­ity of an awk­ward con­fig­ur­a­tion could some­times take a long time to check, and with memor­ies of the nonre­du­cible Shi­m­amoto horse­shoe, they found it con­veni­ent to im­pose on each con­fig­ur­a­tion an ar­ti­fi­cial lim­it of ninety minutes check­ing time on an IBM 370-158 com­puter, or thirty minutes on an IBM 370-168 com­puter. If a con­fig­ur­a­tion could not be proved re­du­cible in this time, it was aban­doned and re­placed by oth­er con­fig­ur­a­tions: find­ing such al­tern­at­ive con­fig­ur­a­tions was usu­ally straight­for­ward. By way of com­par­is­on, they es­tim­ated that check­ing the com­puter out­put of one of the more dif­fi­cult con­fig­ur­a­tions by hand would take someone work­ing a 40-hour week about five years in total.

The last few months were in­deed ex­tremely heavy on com­puter time, but here Ap­pel, Haken, and Koch were for­tu­nate. Prob­ably no oth­er in­sti­tu­tion would have giv­en them twelve hun­dred hours of com­puter time, but the Uni­versity of Illinois’s com­puter cen­ter was very sup­port­ive throughout. Use was also made of the com­puter in the Chica­go branch of the Uni­versity: pro­grams were sent to them overnight and the re­turns were ready by the next morn­ing.

In March 1976 a power­ful new com­puter was bought by the Uni­versity’s ad­min­is­trat­ors. As Haken re­calls, loc­al politi­cians star­ted to ask: “Why does this ad­min­is­tra­tion need a lar­ger com­puter than the sci­ent­ists?”, and the ad­min­is­trat­ors had to prom­ise: “OK, half the time, or whenev­er the thing is not needed by us, the sci­ent­ists can use it”. Since Ap­pel seemed to be the only sci­ent­ist who could get the ma­chine run­ning prop­erly, he was ini­tially al­most its only user, with a use­ful fifty hours of com­puter time over the East­er va­ca­tion. Every­one was happy: the ad­min­is­trat­ors could claim a more bal­anced load­ing of the sys­tem over a 24-hour peri­od, while Ap­pel got all the com­puter time he needed.

In the event, this new com­puter proved to be so power­ful that everything pro­ceeded far more quickly than they had ex­pec­ted, sav­ing them, by their own es­tim­a­tion, a full two years on the re­du­cib­il­ity test­ing. Mean­while, with the help of Haken’s daugh­ter Dorothea, they spent months of ex­haust­ing and stress­ful ef­fort work­ing through the two thou­sand or so con­fig­ur­a­tions that would even­tu­ally form the un­avoid­able set:

One of us wrote a sec­tion, and then the second one was read­ing it over, check­ing it for mis­takes, and bring­ing the er­rors to the at­ten­tion of the one who wrote it, and then the third per­son read it a third time. Read­ing it over was more strenu­ous than writ­ing it, be­cause it went faster, and it was more ex­haust­ing. It was a ter­rif­ic amount of work for three people.

Sud­denly by late June, al­most be­fore they real­ized what was hap­pen­ing, the en­tire job was fin­ished: the Hakens had com­pleted the con­struc­tion of the un­avoid­able set, and with­in two days Ap­pel was able to test the fi­nal con­fig­ur­a­tions for re­du­cib­il­ity. Ap­pel cel­eb­rated their achieve­ment by pla­cing a no­tice on the de­part­ment’s black­board:

Mod­ulo care­ful check­ing it ap­pears that four col­ors suf­fice.

This phrase, four col­ors suf­fice, sub­sequently be­came the de­part­ment’s postal meter slo­gan.

All that re­mained was the de­tailed check­ing, which had to be car­ried out speedily since — not ex­pect­ing the re­du­cib­il­ity test­ing to ad­vance so well — Ap­pel had ar­ranged a sab­bat­ic­al vis­it to France and was due to leave in late Ju­ly, leav­ing them just five weeks to fin­ish the job. Al­though they had not fully real­ized it, time was in­deed of the es­sence, as sev­er­al oth­er map-colorers were with­in strik­ing dis­tance of solv­ing the prob­lem.

At the Uni­versity of Wa­ter­loo, Ontario, Frank Al­laire had the best re­du­cib­il­ity meth­ods around: in Haken’s words, these were even bet­ter than Heesch’s and much bet­ter than ours. Ap­pel and Haken were aware of Al­laire’s su­per­i­or meth­ods, and by 1976 Al­laire was sev­er­al months ahead of them in his in­vest­ig­a­tions in­to re­du­cib­il­ity and was ex­pect­ing to com­plete his solu­tion with­in a few months.

Mean­while, at the Uni­versity of Rhodesia was a former chem­ist, Ted Swart, who was mak­ing ex­cel­lent pro­gress on the four-col­or prob­lem. Swart sub­mit­ted a pa­per to the Journ­al of Com­bin­at­or­i­al The­ory and re­ceived a reply from the Ed­it­or-in-Chief, Bill Tutte, to the ef­fect that Al­laire was work­ing along very sim­il­ar lines. Al­laire and Swart pooled their res­ults and sub­mit­ted a pa­per [e14] just be­fore Haken and Ap­pel’s proof was an­nounced: this de­scribed an al­gorithm for de­term­in­ing the re­du­cib­il­ity of con­fig­ur­a­tions and in­cluded a full list of all re­du­cible con­fig­ur­a­tions with ring-size 10 or less.

Yet an­oth­er per­son who had been de­vel­op­ing some power­ful new meth­ods for tack­ling the four-col­or prob­lem, and who was ex­pec­ted to com­plete his solu­tion with­in a year, was a Har­vard doc­tor­al stu­dent Wal­ter Strom­quist (see [e11]).

Al­though no-one was aware just how close every­one else was to com­plet­ing their solu­tions, Haken and Ap­pel sus­pec­ted that it would be too risky to wait for five months, es­pe­cially if a ru­mor leaked out that they had al­most reached their goal. They guessed that Al­laire, with his su­per­i­or re­du­cib­il­ity meth­ods, was some way ahead of them on that score, but con­fid­ently be­lieved that their strategy of spend­ing nine-tenths of their time on un­avoid­able sets and only one-tenth on re­du­cible con­fig­ur­a­tions (while oth­ers op­er­ated the oth­er way round) still gave them the edge over­all.

But they had no time to lose. Draft­ing in their chil­dren to help they im­me­di­ately set to work. They had high ex­pect­a­tions that, while the check­ing might turn up many ty­pos and the oc­ca­sion­al bad con­fig­ur­a­tion that would need re­pla­cing, there would be no ma­jor dis­asters. Laurel Ap­pel checked through the 700 pages of de­tailed work­ing and found about 800 mis­takes in total, most of them ty­pos, and all but fifty of these she im­me­di­ately cor­rec­ted her­self. As Haken later re­marked:

Some­body has worked one month full-time and found eight hun­dred mis­takes. And then we needed only five days to re­pair all that. This looks so stable — it is this in­cred­ible sta­bil­ity….

Haken and Ap­pel knew by this stage that they were safe: even if a few con­fig­ur­a­tions turned out not to be re­du­cible after all, there was more than enough self-cor­rec­tion in the whole sys­tem for these con­fig­ur­a­tions to be re­place­able eas­ily and quickly. It was not pos­sible for a single faulty con­fig­ur­a­tion, if such ex­is­ted, to des­troy the en­tire edi­fice. In fact, there was so much self-cor­rec­tion in the sys­tem that they ef­fect­ively had many thou­sands of proofs of the four-col­or the­or­em, rather than just one!

Armed with this con­fid­ence, they went pub­lic. On 22 Ju­ly, 1976, just a few days be­fore Ap­pel was due to leave for France, they form­ally in­formed their col­leagues and sent out com­plete pre­prints to every­one in the field. One of the re­cip­i­ents was Bill Tutte. Two years earli­er he had writ­ten an art­icle in the Amer­ic­an Sci­ent­ist [e10] claim­ing that people who used their ap­proach were real op­tim­ists, since the meth­od seemed ex­tremely un­likely to work. But when Tutte heard the news he waxed elo­quent, com­par­ing their achieve­ment with the slay­ing of a fabled Nor­we­gi­an sea mon­ster:

Wolfgang Haken
Smote the Kraken
One! Two! Three! Four!
Quoth he: “The mon­ster is no more”.

Haken and Ap­pel were de­lighted that a math­em­atician of Tutte’s stature should have giv­en his pos­it­ive sup­port so quickly. Tutte’s en­dorse­ment would go a long way to set­ting people’s minds at rest, while a luke­warm re­sponse could have cast ser­i­ous doubts about their solu­tion.

They de­cided to sub­mit the full solu­tion to the Illinois Journ­al of Math­em­at­ics. This was partly be­cause a few years earli­er they had pub­lished a long and tur­gid art­icle in its pages, and they felt that they owed it to the Illinois Journ­al to give it the kudos for pub­lish­ing their solu­tion of this fam­ous prob­lem. But the main reas­on that they wanted it to ap­pear loc­ally was be­cause they wished to be in a po­s­i­tion to sug­gest ap­pro­pri­ate ref­er­ees for their proof. It was clearly in every­one’s in­terest — theirs and the journ­al’s — that a pa­per such as this should be thor­oughly ref­er­eed:

We said to the Illinois Journ­al, “Look, if this thing is wrong, we want to know it as badly as any­one else does, and you’re not go­ing to re­ject it on the grounds of tri­vi­al­ity.”

They agreed with the Ed­it­or that the best people in the world should be se­lec­ted as ref­er­ees — Frank Al­laire for the re­du­cib­il­ity part and Jean May­er in France for the dis­char­ging ar­gu­ments. In France, Ap­pel spent much of his sab­bat­ic­al time in Mont­pel­li­er work­ing painstak­ingly through the de­tails of the proof with Jean May­er, one step at a time, deal­ing with all of May­er’s quer­ies and sug­ges­tions as they arose. On his re­turn in Decem­ber 1976 Ap­pel and Haken set to work re­fin­ing the proof, con­fer­ring with the ref­er­ees, and pre­par­ing the pa­per and its as­so­ci­ated mi­crofiche for pub­lic­a­tion.

Hein­rich Heesch was nat­ur­ally very dis­tressed that Ap­pel and Haken had got there first — not sur­pris­ingly, since their meth­od was es­sen­tially due to him and solv­ing the four-col­or prob­lem had been his goal for more than forty years. But later he be­came very co­oper­at­ive, send­ing Haken his own list of 2669 re­du­cible con­fig­ur­a­tions, to­geth­er with sup­port­ing data on the num­ber of good con­fig­ur­a­tions. Frank Al­laire was also bit­terly dis­ap­poin­ted when Ap­pel and Haken an­nounced their res­ult, as he him­self was near­ing a solu­tion. Moreover, he and Ted Swart had been tak­ing a more sys­tem­at­ic ap­proach, as op­posed to the more hit-and-miss meth­ods of Ap­pel and Haken. But he quickly sup­pressed his own feel­ings for the gen­er­al good, ref­er­ee­ing the re­du­cib­il­ity part con­scien­tiously and con­struct­ively.

Ap­pel and Haken’s pa­per was a sub­stan­tial im­prove­ment on the rough-and-ready pre­print that they had sent out in Ju­ly 1976. In par­tic­u­lar, they dis­covered that their pre­print con­tained sev­er­al “re­peats” of con­fig­ur­a­tions and many in­stances of one con­fig­ur­a­tion ap­pear­ing in­side an­oth­er, so that in each case they could omit the lar­ger one. By weed­ing out these su­per­flu­ous con­fig­ur­a­tions they man­aged to re­duce the ori­gin­al list of 1936 re­du­cible con­fig­ur­a­tions to the 1482 con­fig­ur­a­tions of the pub­lished ver­sion: they later re­duced this num­ber still fur­ther to 1405. However, they saw no point in aim­ing for the “smal­lest pos­sible” num­ber if the total com­puter time was thereby in­creased. As Ap­pel poin­ted out:

If one con­fig­ur­a­tion re­places twelve, but that one con­fig­ur­a­tion takes two hours and the twelve take five minutes, that doesn’t make sense.

Ap­pel and Haken’s solu­tion ap­peared in two parts in the Decem­ber 1977 is­sue of the Illinois Journ­al of Math­em­at­ics [4], [5]. Part I, Dis­char­ging, writ­ten by the two of them, out­lined the over­all strategy of their proof and de­scribed their meth­ods of dis­char­ging for con­struct­ing the un­avoid­able set. Part II, Re­du­cib­il­ity, writ­ten with John Koch, de­scribed the com­puter im­ple­ment­a­tion and lis­ted the en­tire un­avoid­able set of re­du­cible con­fig­ur­a­tions. These were sup­ple­men­ted by a mi­crofiche con­tain­ing 450 pages of fur­ther dia­grams and de­tailed ex­plan­a­tions.

Wolfgang Haken and Ken­neth Ap­pel had achieved their goal: the four-col­or the­or­em was proved.

The Ap­pel–Haken proof of the four-col­or the­or­em was greeted with great en­thu­si­asm: after 124 years one of the most fam­ous prob­lems in math­em­at­ics had fi­nally been solved. But it was also greeted with skep­ti­cism, out­right re­jec­tion, and (more than any­thing else) great dis­ap­point­ment.

Every Au­gust the Amer­ic­an Math­em­at­ic­al So­ci­ety and the Math­em­at­ic­al As­so­ci­ation of Amer­ica used to or­gan­ize a joint sum­mer meet­ing. In 1976 it was held at the Uni­versity of Toronto, and Wolfgang Haken was one of the main speak­ers. A re­port on the event by Don­ald Al­bers [e16] de­scribed the scene:

The el­eg­ant and old lec­ture hall was jammed with math­em­aticians anxious to hear Pro­fess­or Haken give the proof. It seemed like the per­fect set­ting to an­nounce a great math­em­at­ic­al res­ult. He pro­ceeded to out­line clearly the com­puter-as­sisted proof that he and his col­leagues had de­vised. At the con­clu­sion of his re­marks, I had ex­pec­ted the audi­ence to erupt with a great ova­tion. In­stead, they re­spon­ded with po­lite ap­plause!

Re­ac­tion to Haken’s lec­ture was cer­tainly mixed. Ted Swart praised the qual­ity of Haken’s present­a­tion, re­call­ing that the ap­plause was a little more than merely po­lite. But this was by no means the gen­er­al re­ac­tion:

Math­em­atician after math­em­atician ex­pressed un­eas­i­ness with a proof in which a com­puter played a ma­jor role. They were bothered by the fact that more than 1000 hours of com­puter time had been ex­pen­ded in check­ing some 100,000 cases and of­ten sug­ges­ted (hoped?) that there might be an er­ror bur­ied in the hun­dreds of pages of com­puter print outs. Bey­ond that con­cern was a hope that a much short­er proof could be found.

The re­port con­cluded:

It seems that the com­puter-as­sisted work of Ap­pel, Haken, and Koch on the well-known Four-Col­or Prob­lem may rep­res­ent a wa­ter­shed in the his­tory of math­em­at­ics. Their work has been re­mark­ably suc­cess­ful in for­cing us to ask What is a Proof Today?

It was clear that Ap­pel and Haken’s solu­tion of the four-col­or prob­lem had cre­ated a new situ­ation in math­em­at­ics. Is it a proof? And if so, how do we know that it is a proof? Con­cerns about it, and par­tic­u­larly about its use of the com­puter, con­tin­ued to rumble on — and still do. Can a proof be con­sidered val­id if it can­not be checked by hand?

As math­em­at­ic­al proofs have be­come longer and com­puters are used more widely, the whole ques­tion of sur­vey­ab­il­ity has be­come fraught with dif­fi­culties. A com­puter that per­forms ex­tens­ive but com­pletely routine tasks may cer­tainly be con­sidered at least as re­li­able than a hu­man check­ing by hand a proof that is long and com­plic­ated or breaks up in­to a large num­ber of spe­cial cases. In Ted Swart’s words:

Hu­man be­ings get tired, and their at­ten­tion wanders, and they are all too prone to slips of vari­ous kinds…Com­puters do not get tired.

But sur­vey­ab­il­ity has not been the only prob­lem caused by the Ap­pel–Haken proof. Sev­er­al math­em­aticians have com­plained that their proof is not suf­fi­ciently “trans­par­ent”. Among these was Ian Stew­art, the well-known writer on math­em­at­ics, who com­plained that it did not ex­plain why the the­or­em is true, partly be­cause it was too long for one to grasp all the de­tails, and partly be­cause it seemed to have no struc­ture:

The an­swer ap­pears as a kind of mon­strous co­in­cid­ence. Why is there an un­avoid­able set of re­du­cible con­fig­ur­a­tions? The best an­swer at the present time is: there just is. The proof: here it is, see for your­self. The math­em­atician’s search for hid­den struc­ture, his pat­tern-bind­ing urge, is frus­trated.

What every­one did agree on, however, was that the Ap­pel–Haken proof could not be de­scribed as beau­ti­ful or el­eg­ant math­em­at­ics. In his cel­eb­rated book A Math­em­atician’s Apo­logy [e8], the cel­eb­rated Eng­lish math­em­atician G. H. Hardy had once as­ser­ted:

There is no per­man­ent place in the world for ugly math­em­at­ics.

 — and even Ap­pel did not de­mur from this in re­spect to his own proof:

There were people who said, “This is ter­rible math­em­at­ics, be­cause math­em­at­ics should be clean and el­eg­ant”, and I would agree. It would be nicer to have clean and el­eg­ant proofs.

However, while every­one would like to see a non­com­puter solu­tion of the four-col­or the­or­em, such a solu­tion along the lines of the Ap­pel–Haken proof is al­most cer­tainly un­at­tain­able — not least be­cause any un­avoid­able set of re­du­cible con­fig­ur­a­tions must in­clude con­fig­ur­a­tions with ring-size 12 or more, as we saw earli­er. For a non­com­puter proof, new ideas are needed, and such ideas have not yet been forth­com­ing.

Fol­low­ing his lec­ture at the Toronto meet­ing, Haken spent a lot of time tour­ing the United States, ex­plain­ing the de­tails of their solu­tion. Ap­pel was do­ing a sim­il­ar thing in Europe, giv­ing lec­tures in France and Eng­land. These lec­tures were in­form­at­ive and con­vin­cing to those who at­ten­ded. But fol­low­ing the ap­pear­ance of their un­ortho­dox proof, Ap­pel and Haken were some­times made to feel most un­wel­come. The most dra­mat­ic oc­ca­sion oc­curred when the head of a math­em­at­ics de­part­ment re­fused to al­low them to meet his gradu­ate stu­dents on the grounds that:

Since the prob­lem had been taken care of by a totally in­ap­pro­pri­ate means, no first-rate math­em­atician would now work any more on it, be­cause he would not be the first one to do it, and there­fore a de­cent proof might be delayed in­def­in­itely. It would cer­tainly re­quire a first-rate math­em­atician to find a sat­is­fact­ory proof, and that was now im­possible.

They were made to feel that they had done something very wicked, and that the in­no­cent souls of stu­dents needed to be pro­tec­ted from their bad in­flu­ence.

Oth­er pub­lic­a­tions ap­peared in 1977. As well as brief re­ports on their solu­tion in the Bul­let­in of the Amer­ic­an Math­em­at­ic­al So­ci­ety [2] and Dis­crete Math­em­at­ics [3], Ap­pel and Haken wrote a more pop­u­lar art­icle on “The solu­tion of the four-col­or-map prob­lem” [Ed­it­or’s note: see the art­icle here] for the read­ers of Sci­entif­ic Amer­ic­an [6]: this is still one of the clearest de­scrip­tions of their ap­proach to solv­ing the prob­lem. An­oth­er ac­count ap­peared in [7], and a fur­ther re­search pa­per in [8]. Around the same time, a second book on the four-col­or prob­lem was pub­lished: The Four-Col­or Prob­lem: As­saults and Con­quests, by Thomas Saaty and Paul Kain­en [e13].

By the early 1980s, ru­mors were be­gin­ning to spread that there was a ma­jor er­ror in Ap­pel and Haken’s proof of the four-col­or the­or­em. In view of its com­plex­ity, many er­rors might have been ex­pec­ted to ap­pear, but this hardly happened. These ru­mors prob­ably arose from a mis­take (no­ticed by Ul­rich Schmidt, a Ger­man en­gin­eer­ing stu­dent) that took two weeks for Haken to cor­rect, and a draw­ing er­ror in one con­fig­ur­a­tion, but oth­er than these and a few mis­prints no sig­ni­fic­ant er­ror has ever been found in their proof.

In 1986 Ap­pel and Haken re­ceived a let­ter from the Ed­it­or of the Math­em­at­ic­al In­tel­li­gen­cer, who had heard these ru­mors that something was wrong with the proof and in­vited them to set the re­cord straight. Wel­com­ing such con­tro­versy, they replied:

With this kind of­fer we can­not but com­ply, al­though it is a pity to spike a good ru­mor. Math­em­at­ic­al ru­mors do add in­terest and ex­cite­ment to the con­ver­sa­tion at math­em­at­ic­al meet­ings. However, the ru­mors about the Four-Col­or The­or­em seem to be based on a mis­in­ter­pret­a­tion of the res­ults of the in­de­pend­ent check of de­tails of the proof by U. Schmidt.

The res­ult was “The four col­or proof suf­fices”, an up­beat art­icle ex­plain­ing the er­ror and de­scrib­ing their meth­ods in some de­tail [9]. They fol­lowed this in 1989 by their last word on the sub­ject, a hefty tome pub­lished by the Amer­ic­an Math­em­at­ic­al So­ci­ety en­titled Every Planar Map is Four Col­or­able [10]: this sup­plied sev­er­al more de­tails of the proof, proved some re­lated res­ults, cor­rec­ted all the er­rors that had aris­en, and in­cluded a prin­ted ver­sion of all their mi­crofiche pages.

In 1994 Neil Robertson, Daniel Sanders, Paul Sey­mour, and Robin Thomas ad­ded an ex­cit­ing new chapter to the four-col­or saga. For the pre­vi­ous ten years, mem­bers of this group had been ob­tain­ing some spec­tac­u­lar res­ults in graph the­ory, and they now turned to the four-col­or prob­lem be­cause it was re­lated to oth­er work in which they were in­volved.

They were con­cerned that Ap­pel and Haken’s proof was still not fully ac­cep­ted, as­sert­ing that there re­mained some doubt as to its valid­ity. The main reas­on was not that the proof in­volved a com­puter, even though a full check of the re­du­cib­il­ity part would have in­volved in­put­ting 1482 con­fig­ur­a­tions by hand in­to the com­puter and a lot of pro­gram­ming to test each one for re­du­cib­il­ity. It was the un­avoid­ab­il­ity ar­gu­ments that caused them most con­cern: the dis­char­ging al­gorithm that Ap­pel and Haken had car­ried out by hand was very com­plic­ated and no-one had ever made an in­de­pend­ent check of it all.

After a week of work­ing through the de­tails of the Ap­pel–Haken proof they gave up. They de­cided that it would be much more fun, and much more in­struct­ive, to dis­cov­er their own proof, us­ing the same gen­er­al ap­proach that Ap­pel and Haken had used. It took them a whole year to com­plete the work, but their even­tu­al proof was short­er and more ro­bust than its pre­de­cessor [e17].

The un­avoid­able set that they ob­tained con­tains only 633 re­du­cible con­fig­ur­a­tions — they could have re­duced it fur­ther, but only at the ex­pense of more com­puter time. Moreover, their dis­char­ging pro­ced­ure for prov­ing un­avoid­ab­il­ity in­volved only 32 dis­char­ging rules, in­stead of the 487 used by Ap­pel and Haken. Be­cause they con­sidered com­puter proofs of long and com­plic­ated res­ults to be more re­li­able than hand-checked ones, they used the com­puter for both the un­avoid­ab­il­ity and re­du­cib­il­ity parts of the proof. What is more, all the steps in their proof can be ex­tern­ally veri­fied by any­one on their home com­puter in just a few hours.

In Au­gust 1998, shortly after their new proof ap­peared, one of its au­thors, Robin Thomas, wrote an in­ter­est­ing art­icle giv­ing “An up­date on the four-col­or the­or­em” [e18] in the No­tices of the Amer­ic­an Math­em­at­ic­al So­ci­ety [Ed­it­or’s note: see the art­icle here], out­lining its main ideas and em­phas­iz­ing the the­or­em’s im­port­ance by de­scrib­ing some res­ults from oth­er branches of math­em­at­ics (the di­vis­ib­il­ity of in­tegers, the al­gebra of three-di­men­sion­al vec­tors, and matrices and tensors) that sur­pris­ingly turn out to be equi­val­ent to it.

The im­proved meth­ods em­ployed by Robertson and his team led to a more ef­fi­cient al­gorithm for col­or­ing maps. Ap­pel and Haken’s ap­proach had giv­en rise to a quart­ic al­gorithm for map col­or­ing: this means that if a map has \( n \) coun­tries, then the run­ning time re­quired for col­or­ing the map is pro­por­tion­al to \( n^4 \). The more ef­fi­cient meth­ods of Robertson’s cowork­ers led to a quad­rat­ic al­gorithm, for which the run­ning time is pro­por­tion­al to \( n^2 \). The res­ult­ing im­prove­ments are ap­par­ent from the fol­low­ing table which com­pares the run­ning times for vari­ous val­ues of \( n \) for a com­puter per­form­ing a mil­lion cal­cu­la­tions per second: \[ \begin{array}{lccc} \hline &n = 10 &n = 100 &n = 1000\\ \hline n^2 &0.0001 \,\text{seconds} &0.01 \,\text{seconds} &1 \,\text{second}\\ n^4& 0.01 \,\text{seconds}& 1 \,\text{minute}, 40 \,\text{seconds}& \text{over } 11 \frac{1}{2} \,\text{days}\\ \hline \end{array} \]

More re­cently, good pro­gress has been made in a num­ber of dir­ec­tions. We men­tion two of these here.

We re­call that a con­fig­ur­a­tion is \( D \)-re­du­cible if every col­or­ing of the sur­round­ing ring of coun­tries can be ex­ten­ded to the coun­tries of the con­fig­ur­a­tion, dir­ectly or after some Kempe-in­ter­changes of col­or, and that it is \( C \)-re­du­cible if it can be proved to be re­du­cible after it has been mod­i­fied in some way. Since \( D \)-re­du­cible con­fig­ur­a­tions are much easi­er to deal with, we may ask wheth­er there is a proof of the four-col­or the­or­em that in­volves only \( D \)-re­du­cible con­fig­ur­a­tions.

This ques­tion was answered in the af­firm­at­ive by John P. Stein­ber­ger [e21] in 2008. In­ev­it­ably it in­volved more con­fig­ur­a­tions and more dis­char­ging al­gorithms than had earli­er proofs, and the au­thor needed to con­sider con­fig­ur­a­tions with lar­ger ring-size. The fol­low­ing table sum­mar­izes the dif­fer­ences: \[ \begin{array}{lccc} \hline & \text{No. of configurations} &\text{No. of discharging rules} & \text{Largest ring-size}\\ \hline \text{Appel and Haken} & 1482 & 487 &14\\ \text{Robertson et al.} &633 &32& 14\\ \text{Steinberger} & 2832&42&16\\ \hline \end{array} \]

So now that the four-col­or prob­lem has been proved, what else is there for map-colorers to do? This ques­tion was asked back in 1978 in an art­icle by Bill Tutte [e15]:

I ima­gine one of them out­grib­ing in des­pair, cry­ing “What shall I do now?” To which the prop­er an­swer is “Be of good cheer. You can con­tin­ue in the same gen­er­al line of re­search.”

For the four-col­or the­or­em is by no means the end of the line — it is in­deed more of a be­gin­ning. In spite of its enorm­ous dif­fi­culty, it is just one spe­cial in­stance of some much harder prob­lems that de­vel­op the ideas of the four-col­or the­or­em in new and ex­cit­ing dir­ec­tions (such as find­ing proofs for Had­wi­ger’s con­jec­ture and the five-flow con­jec­ture), and on these prob­lems good pro­gress is already be­ing made.

With these thoughts of the fu­ture in our minds, we leave our last po­et­ic mus­ings to Bill Tutte:

The Four-Col­our The­or­em is the tip of the ice­berg,
the thin end of the wedge
and the first cuckoo of Spring.

Much of this art­icle is de­rived from the au­thor’s book, where fur­ther de­tails can be found: Robin Wilson, Four Col­ors Suf­fice (re­vised col­or edi­tion), Prin­ceton Sci­ence Lib­rary, Prin­ceton Uni­versity Press, 2013.

Much ma­ter­i­al re­lat­ing to Heesch can be found in the bio­graphy: Hans-Günther Bi­galke, Hein­rich Heesch: Kristallgeo­met­rie, Par­ket­tier­ungen, Vi­er­farben­forschung, Birkhäuser, Basel, 1988.

Many of the quo­ta­tions are taken from un­pub­lished in­ter­views by Don­ald MacK­en­zie with Ap­pel, Haken, Swart, and oth­ers (see also [e19]).