by Hyman Bass
Mathematicians are conventionally measured by the depth and creativity of their contributions to research. On these grounds alone Kaplansky is a towering figure. But another, perhaps comparably important, way to contribute to the advancement of mathematics lies in the building of human capacity, in the formation of productive young researchers, through teaching, mentoring, and written exposition. In this regard, Kaplansky, with an astonishing fifty-five doctoral students (among whom I count myself), and 627 mathematical descendants, has had a singular impact on our field.
Kap was born March 22, 1917, in Toronto, the youngest of four children, shortly after his parents had emigrated to Canada from Poland. His father, having studied to be a rabbi in Poland, worked in Toronto as a tailor. His mother, with little schooling, was enterprising and built up a business, “Health Bread Bakeries”, that supported (and employed) the whole family.
Kap showed an early and evolving talent for music, as he himself recounts [e1]:
At age four, I was taken to a Yiddish musical, Die Goldene Kala (The Golden Bride). It was a revelation to me that there could be this kind of entertainment with music. When I came home I sat down and played the show’s hit song. So I was rushed off to piano lessons. After 11 years I realized there was no point in continuing; I was not going to be a pianist of any distinction…. I enjoy playing piano to this day…. God intended me to be the perfect accompanist — or better, the perfect rehearsal pianist. I play loud, I play in tune, but I don’t play very well.
Indeed, Kap became a popular accompanist and performer through much of his career. At one point, to demonstrate the virtues of a structure he discovered common to his favorite songs, he says, “I tried to show that you could [use it to] make a passable song out of such an unpromising source of thematic material as the first 14 digits of \( \pi \).” The resulting “Song about \( \pi \)” was later given lyrics by Enid Rieser and is often performed by Kap’s daughter, Lucy, herself a popular folk singer-songwriter [e2]. Some more personal family vignettes of Kap can be found below in Lucy’s reminiscences of her father.
As a senior at the University of Toronto in 1938, Kap won the very first Putnam Competition, as did the Toronto team. This won him a fellowship to Harvard, where he earned his Ph.D. in 1941, under the direction of Saunders Mac Lane. He stayed on as a Benjamin Peirce Instructor till 1944, when Mac Lane brought him to the Applied Mathematics Group at Columbia University in 1944–45, which was doing work to support the war effort. Kap recounts, “So that year was spent largely on ordinary differential equations. I had a taste of real life and found that mathematics could actually be used for something.”
From there Kap moved to the University of Chicago in the fall of 1945, where he remained till his retirement in 1984, having chaired the department during 1962–67. A year after Kap’s arrival, Marshall Stone came to Chicago to direct and build up the mathematics department, ushering in what some have called “the Stone Age”. Stone made four gigantic appointments — Saunders Mac Lane, Antoni Zygmund, André Weil, and Shiing-Shen Chern — followed by waves of talented young faculty and graduate students. Among the younger colleagues who greatly influenced Kap were Irving Segal, Paul Halmos, and Ed Spanier. Kap’s life style, outside his family and music, was rigorous and austere. He scheduled classes and meetings at (defiantly) early hours of the morning. Daily swimming was a lifelong practice; he loved the Lake Michigan shoreline. Lunch was lean in time as well as substance. With students he was generous and indulgent in mathematical conversation, but entertained little else.
After Chicago, Kap, succeeding Shiing-Shen Chern, became the second director of the Mathematical Sciences Research Institute (MSRI) in Berkeley, 1984–1992. Also in 1984, Kap was elected president of the AMS. So we see here a career trajectory from a precocious college student to a dedicated, well established and prolific researcher, to a leader of some of the premier institutions of the profession. Along the way, Kap was honored by election to the National Academy of Sciences and to the American Academy of Arts and Sciences, and he was named an honorary member of the London Mathematical Society. In 1989 the AMS awarded him the Steele Prize, Career Award.
To understand Kap’s mathematical accomplishments, it is important to speak of his students as well as his publications, to distinguish and compare what these two records tell us. Kap’s mathematical work is distributed across several different areas of mathematics. For purposes of surveying them, I have somewhat arbitrarily grouped them as follows, the major areas in bold font:
| TA : | Topological algebra, including operator algebras, *-algebras, locally compact rings, etc. |
| Q : | Quadratic and higher forms, both abstract and arithmetic aspects |
| C : | Commutative and homological algebra |
| R : | Ring theory (noncommutative) |
| Lie : | Lie theory-groups and algebras, including infinite dimensional and characteristic p |
| # : | Combinatorics and number theory |
| M : | Module theory, including abelian groups |
| L : | Linear algebra |
| G : | Miscellaneous, including general topology, group theory, game theory |
| PS : | Probability and statistics |
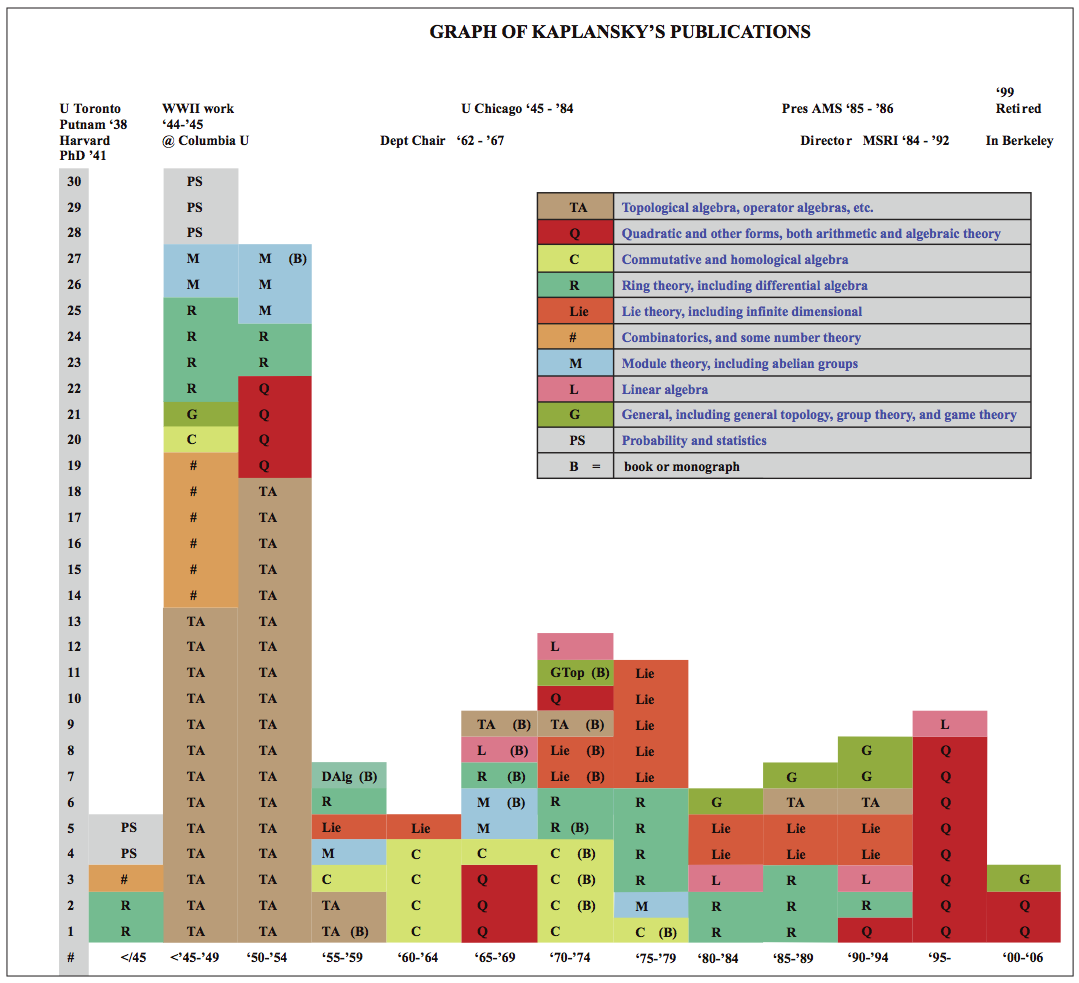
In this chronological chart I have color-coded Kap’s journal articles, books, and monographs according to which of these areas they belong. The data are taken from MathSciNet. Not included are the numerous contributions to the Problem sections of the American Mathematical Monthly; Kap remained throughout a virtuoso problem solver and contributor.
Several remarkable things stand out from this chart.
As a fresh Ph.D during the years of WWII, Kap published, beyond his dissertation (on maximal fields with valuation), a small but interesting mix of papers on combinatorics and on probability and statistics, perhaps in part influenced by his applied work at Columbia.
Then, in the decade 1945–54 there is an extraordinary outpouring of publications, predominantly in what we are calling topological algebra. In fact, in the four years 1948–52, Kap published thirty-two papers! Some of this may have been backlog from the war years, but it is an astonishing ensemble of cutting-edge work in this area. Kap’s general inclination was to algebraically axiomatize the various structures of concern to functional analysts, in the program launched earlier by Murray and von Neumann. Dick Kadison [e3] writes in some detail about this phase of Kap’s work.
Kap’s work in pure noncommutative ring theory is a persistent, but relatively modest theme in his work. One of his most influential papers, on “Rings with polynomial identity”, opened an important branch of noncommutative algebra. Here he proves the fundamental result that a primitive algebra with polynomial identity is finite dimensional over its center.
Lie theory, in its many aspects, is another important strand. This includes work on the classification of simple Lie algebras in characteristic \( p \), lecture notes on the solution of Hilbert’s Fifth Problem, and work, partly in collaboration with the physicist Peter Freund, on graded Lie algebras, super-symmetry, and related classification problems. Peter Freund writes vividly below about their collaboration.
Quadratic (and higher) forms: This subject, from the beginning to the end of Kap’s career, was dear to his heart. This interest was first inspired by his attending L. E. Dickson’s lectures in number theory and quadratic forms at Chicago in the 1940s. It was rekindled during the years of his retirement, when he turned to the arithmetic theory of such forms, partly in collaboration with William Jagy. A charming account of a significant piece of this work can be found in the contribution of Manjul Bhargava below.
In the eyes of many mathematicians today, commutative and homological algebra is the field with which they now most associate Kaplansky’s name. Yet we see that its (yellow) color occupies remarkably little of the chart of publications. How can we explain this paradox? Well, for one thing, Kap’s publications in this area include several books and monographs (lecture notes), and these contain a number of new results and methods that were not elsewhere published. This also reflects the fact that Kap was generating mathematics in this rapidly evolving field more through instruction than through papers written in solitude. And so what he was producing mathematically was significantly embodied in the work of the students who were learning from him.
We can see this phenomenon in the next chart of Kap’s Ph.D. students, again color-coded by the areas of their dissertations.
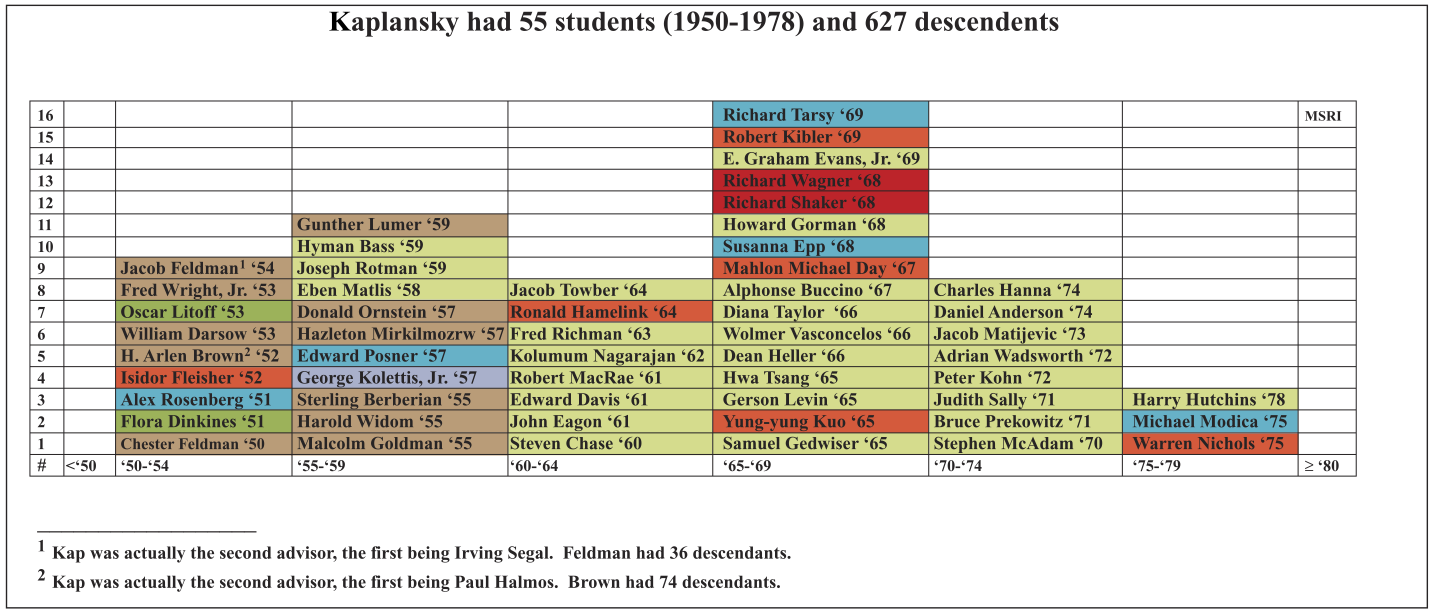
The first thing to notice in comparing these two charts is that the “relative masses” of topological algebra and commutative algebra have been approximately reversed, of course with a time shift. In topological algebra, Kap was a pioneer and a major, intensely productive, conceptual developer of the field. In commutative and homological algebra, in contrast, the field was already in rapid motion, into which Kap boldly ventured as more of an apprentice, guiding a flock of similarly uninitiated graduate students and postdocs with him. Homological algebra was spawned from algebraic topology. In the hands of Eilenberg, Mac Lane, Grothendieck, and others it evolved into a new branch of algebra, embracing category theory and other new constructs. Meanwhile, the Grothendieck–Serre reformulation of algebraic geometry demanded that its foundations in commutative algebra be deepened and expanded.
A basic new concept of homological algebra was that of global homological dimension, a new ring-theoretic invariant. This turned out to be uninteresting for the most investigated rings, finite dimensional (noncommutative) algebras. On the other hand, a landmark discovery (of Auslander–Buchsbaum and Serre) was that, for a commutative noetherian local ring \( A \), the global dimension of \( A \) is finite if and only if \( A \) is regular (the algebraic expression of the geometric notion of nonsingularity). This equivalence, and Serre’s homological formulation of intersection multiplicities, firmly established homological algebra as a fundamental tool of commutative algebra. However, these developments were known mainly on a Cambridge (MA)–Paris-axis. It was in this context that Kap offered a Chicago graduate course introducing these new ideas, methods, and results, then still very much in motion. Use of these methods led to the general proof (by Auslander–Buchsbaum) of unique factorization for all regular local rings. Kap’s course, and its sequels, lifted a whole generation of young researchers (myself included) into this field. This played out for Kap over the next two decades, with many students and several books to show for it.
In mathematical style, Kap was a problem solver of great virtuosity. For course goals he sought problems, and theorems of great pedigree, and probed them deeply. His main focus was on proofs (pathways), more than on theorems (destinations). He sought geodesics, and the most economic (high mileage) means to get there. Proof analysis led to double-edged kinds of generalization/axiomatization:
A given proof yields more than claimed. The given hypotheses deliver more than the stated theorem promises.
The hypotheses can be weakened. We can get the same results more cheaply, and so more generally.
The strength of this disposition was perhaps sometimes over-zealous, pushing toward “premature maturation” of the mathematics. But it was an effective mode of instruction, yielding powerful conceptual command of the territory covered.
As the record above indicates, and the testimonials below will affirm, Kap was a gifted teacher, mentor, and writer. Here are a few of the things he himself has said in reflection on this.
I like the challenge of organizing my thoughts and trying to present them in a clear and useful and interesting way. On the other hand, to see the faces light up, as they occasionally do, to even get them excited so that maybe they can do a little mathematical experimentation themselves — that’s possible, on a limited scale, even in a calculus class.
Advice to students: “Look at the first case, the easiest case that you don’t understand completely. Do examples, a million examples, ‘well chosen’ examples, or ‘lucky’ ones. If the problem is worthwhile, give it a good try — months, maybe years if necessary. Aim for the less obvious, things that others have not likely proved already.”
And: “Spend some time every day learning something new that is disjoint from the problem on which you are currently working (remember that the disjointness may be temporary). And read the masters.”
When a great mathematician has mastered a subject to his satisfaction and is presenting it, that mastery comes through unmistakably, so you have an excellent chance of understanding quickly the main ideas. [He cites as examples, Weil, Serre, Milnor, Atiyah.]
… the thing that bedevils the mathematical profession — the difficulty we have in telling the world outside mathematics what it is that mathematicians do. And for shame, for shame, right within mathematics itself, we don’t tell each other properly.
And here is a sampling of how Kap was seen by others, including some of his students:
“He was not only a fantastic mathematician but a marvelous lecturer, and he had a remarkable talent for getting the best out of students.”
— Richard G. Swan
“I knew Kaplansky in his later years, and also through some of his books. Cheerful, gracious, and elegant are some of the words that come to mind when I think of him.”
— Roger Howe
“The mathematical community in India is shocked to have news of the demise of Professor Irving Kaplansky. We all feel very sad at this irreparable loss. Professor Kaplansky was a source of inspiration for mathematicians around the world. He will no doubt live for all time through his mathematical contributions. We will miss his personal wit, charm and warm personality.”
— I. B. S. Passi (President, Indian Mathematical Society)
“I did know about the work of Emmy Noether and it may have influenced my choice of area, algebra, although I think the teaching of Irving Kaplansky was what really inspired me.”
— Vera Pless
Kaplansky’s books “have one feature in common. The content is refreshing and the style of exposition is friendly, informal (but at the same time mathematically rigorous) and lucid. The author gets to the main points quickly and directly, and selects excellent examples to illustrate on the way.”
— Man Keung Siu
“I learnt from his books in my youth, and would not have survived without them. Even today, I ask my students to read them, to learn the ‘tricks’ of the trade.”
— Ravi Rao
“Kaplansky was one of my personal heroes: during my student years, I discovered his little volume on abelian groups and noticed that algebra too has stories to tell…”
— Birge Huisgen-Zimmermann
Kap as a Thesis Advisor: “I was very young and very immature when I was Kap’s student. I’m deeply indebted to Kap for putting up with me and helping me to develop in my own eccentric way. I asked Kap for a thesis problem that didn’t require any background and, surprisingly, he found one with enough meat in it to allow me to get a feeling for doing research.
“It wasn’t until I had my own thesis students that I realized how hard it must have been to accommodate my special needs and help me develop in my way, not in his way.”
— Donald Ornstein (Kap Ph.D., 1957)
For me Kap’s transition from course instructor to thesis advisor was almost imperceptible, since I had become deeply engrossed in his courses on commutative and homological algebra and questions about projective modules, an exciting territory wide open for exploration, and for which Kap had laid a solid groundwork. He did float a few other problems to me, such as the structure of certain infinite dimensional Lie algebras, whose significance I only later came to appreciate. But I didn’t take that bait then. He was a generously available and stimulating advisor, often sharing promising ideas that he had not yet had time to pursue. What I remember most of that time is the brilliance of his courses, and the richness and excitement of the mathematical milieu that he had created among his many students then. This milieu powerfully amplified the many mathematical resources that Kap had to offer. I think that it is fair to say that Kap’s students are an important part of his oeuvre. One could hardly have asked for a better teacher and advisor.