by Cathleen S. Morawetz
I could have chosen to speak about the progress and changes in applied mathematics that have taken place in the years since the MAA was founded. I have chosen instead to speak about these particular giants of applied mathematics not only because they represent a certain period and a certain influence but because they attained their distinction in very different ways. These people divide into two groups. Those who did nothing or nearly nothing but applied mathematics and those who divided their time between pure and applied mathematics. The first kind is exemplified par excellence by Sir Geoffrey Taylor and Theodore von Karman (he might be annoyed to have the label mathematician) and the examples of the second kind are John von Neumann, Norbert Wiener and Kurt Friedrichs. I will also say if time permits a few words about my father, John L. Synge since there is no question that I learned a lot from him about attitude and action in applied mathematics. I might add that he was chairman of mathematics on this campus from 1943 to 1947.
Before describing the first two of these men — I would like to say a word or two about the subject applied mathematics. This is a term that has different meanings attached to it by both its friends and enemies. Some people like to call it mathematics of the real world (an unattractive expression but at least fairly general), others think of it as being useful and still others use the term as equivalent to lack of rigor.
I wish I could avoid the expression “applied” altogether, but it’s there and the meaning that I attach to it is:
It is mathematics.
It is connected to some other science including engineering science.
I then proceed to strip it down and I exclude statistics. If I did not want to talk about v. Neumann I would also exclude computer science. And I think computer scientists would most definitely agree.
The other sciences range all over: medicine, cryptography, economics, and I think we can be happy to embrace as much as we can.
What distinguishes pure mathematics is that it is exploring mathematics for itself. But I have yet to see in the flesh a pure mathematician who is not ecstatic with delight if someone can apply his result to some other science.
So I have picked my giants mainly on the basis of this distinction between pure and applied. But I have also picked them on the basis of my own knowledge and I confess the possibility of reminiscing.
I must have been interested at an early age in the struggles of the little department of applied mathematics in Toronto that my father chaired. As an undergraduate I remember asking him how many applied mathematicians there were in North America and he replied with the question “You mean excluding those who just do Laplace Transforms.” I have forgotten how many constituted the remainder but it was an insignificant minority of the mathematics community.
Let me start with the oldest of my group and I’ll bet an unsung hero in most mathematical halls. Geoffrey Ingram Taylor, born in 1886, was the grandson of George Boole, so mathematics cannot have been strange to him. He also had a mathematical aunt, Boole’s youngest daughter who published her first paper in geometry in her old age. (I imagine that her father was her teacher). Geoffrey Taylor took the natural science tripos not the mathematical tripos at Cambridge. I have wondered if he was not discouraged from pure mathematics by the situation of his distinguished grandfather who got his first position at the advanced age of 36 in that outpost of the British empire, the University of Cork in Ireland. Taylor received a fellowship at Cambridge in 1908 and there he stayed the rest of his life. In 1911 he was scientific crew for a trip to the Arctic on the H.M.S. Scotia. There he not only enjoyed the making of measurements in the middle of nature but he got started on his study of turbulence. He was fascinated by the outpouring of smoke from the ship’s funnel.
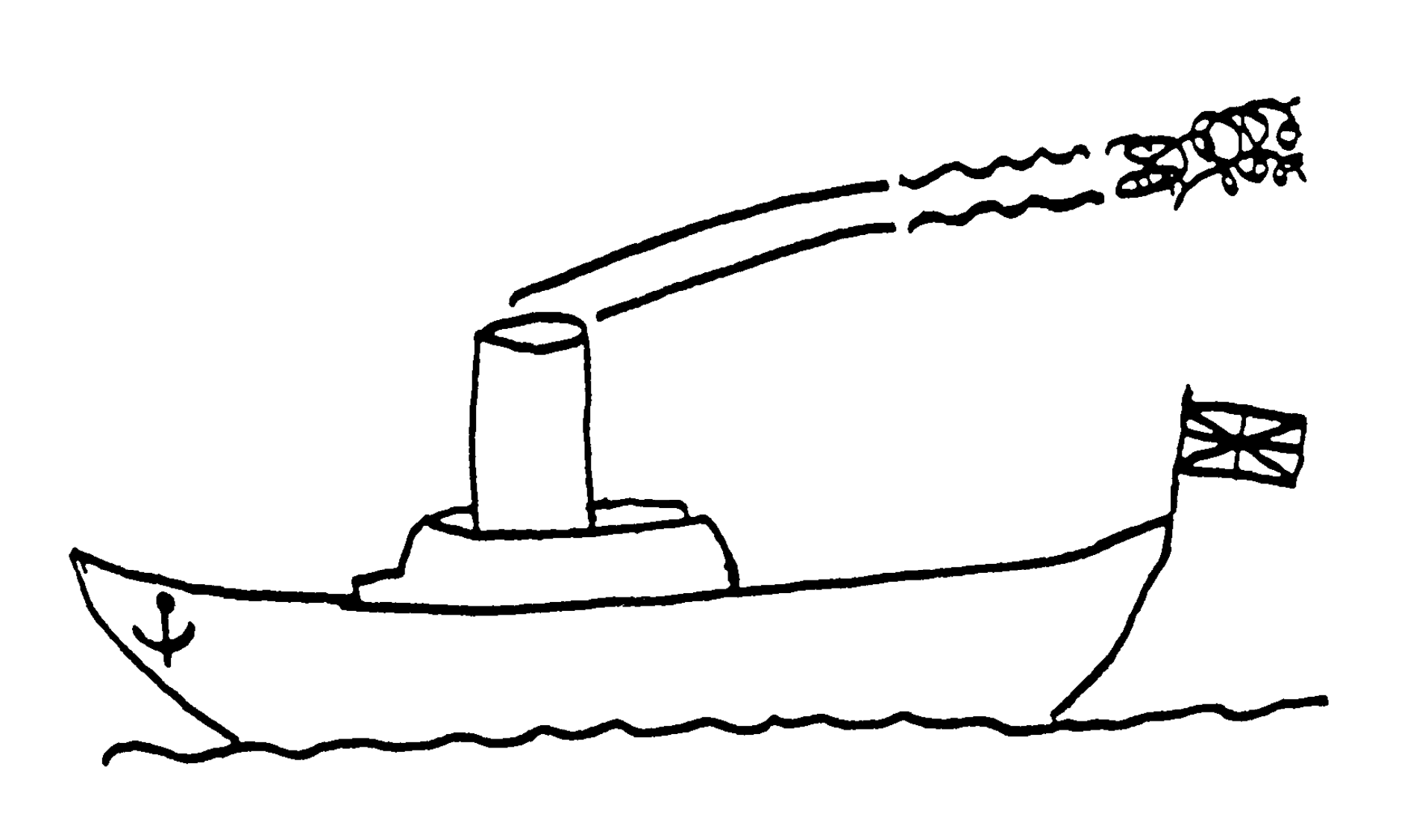
I recently had the opportunity to get equally fascinated. Twice a day a local steamer plies its way past my summer cottage. And this is what I see on a windless day, Figure 1, and I suppose that is what Taylor saw.
In the beginning you have a plume of smoke, a layer of air and under it a layer of hot air and smoke which has lower density and under that again air.
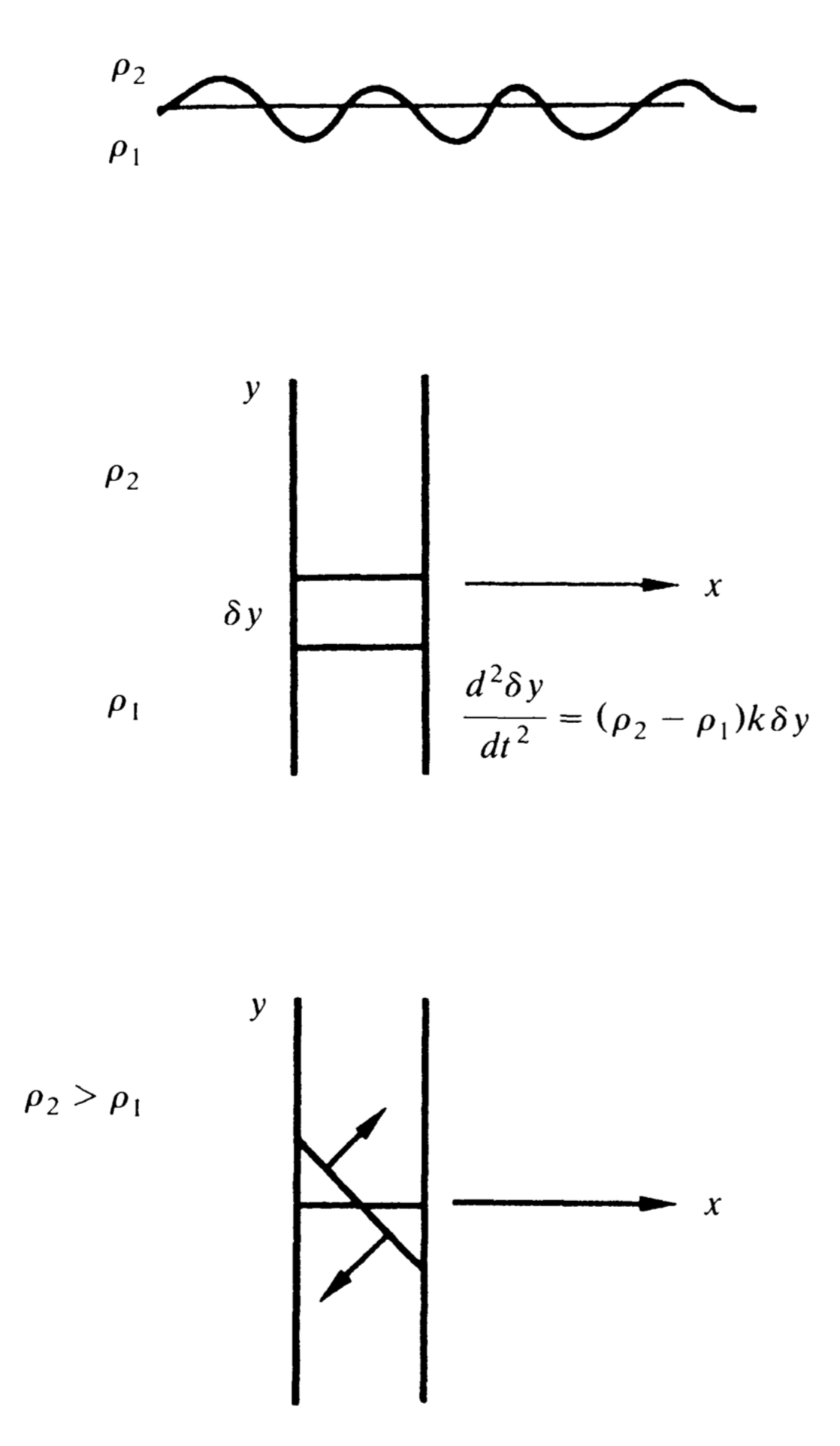
Let us just look at one surface separating gas at different densities as in Figure 2a. Just think of these two layers between two walls separated by a surface \( S \) as in Figure 2b. If we displace the surface by changing its level then the increased pressure on the surface is the difference in the weight of the water above the surface and thus proportional to \[ \delta y(\rho_2-\rho_i) . \] where \( \delta y \) is the difference in level. The acceleration of the surface will be proportional to this force. \begin{equation*} \frac{d^2}{dt^2}\delta y =k(\rho_2-\rho_1)\delta y. \end{equation*} If \( \rho_2 > \rho_1 \) there is exponential growth in time proportional to \[ \sqrt{k}(\rho_2-\rho_1) .\] If \( \rho_2 < \rho_1 \) things are stable.
So we are not surprised that the upper layer of the smoke plume is unstable. But it is really worse than that. Disturb the surface by tilting it as in Figure 2c. Then the pressure will form a torque if \( \rho_2 > \rho_1 \) that makes the surface tilt still more. So it is more unstable. I won’t bore you with the large number of equations you have to write down to do this problem fully. You assume there is a ripple of some prescribed wave length in the surface, again as in Figure 2a and you find the corresponding exponents in time growth. There is no growth if \( \rho_2 < \rho_1 \) but if we have the Taylor situation, every wave length (sufficiently small) produces exponential growth at a rate proportional to the inverse of the wave length.
So this pair of layers is not just unstable. The initial value problem is ill-posed (but that is a long story whose answer is coming slowly now). And so the smoke becomes turbulent very soon.
Having settled the instability in this case (Rayleigh–Taylor), Taylor studied many other problems of stability. Then he went on to formulate a theory for what happens after the flow becomes turbulent.
He introduced the fundamental concept of mixing length and various correlations. Work that influenced Wiener’s work and Taylor himself in turn was influenced by Wiener. Primarily his interest in applied mathematics was in understanding nature by mathematical means and for him much of nature was fluid.
I met him in his lab in 1953 in Cambridge. He delighted in showing me a big trough with a huge kind of paddle for making waves. (I should add he had an incredibly able technician to help him make things.) He also had an uncanny ability to find the right mathematical models always reducing his answers to something currently computable.
One of the amusing tales of my visit is that he could not invite me as a woman, to lunch in the Commons, a completely masculine stronghold, so instead he arranged a lunch for a small group in a student’s room — something that in America would have at that time been completely forbidden.
I saw him again, I think in 1972, in Poland at a conference in his honor. To please him he was taken sailing, his lifelong hobby, and being myself an aficionado of that sport I was particularly impressed that a man of 84 could jibe so elegantly.
By the way, many people who know all about Taylor instability do not know that he designed an anchor, still in common use; it folded better and could be stored less awkwardly. And it also held. He left a legacy not only in his own work but in the work of his scientific children and grandchildren especially G. K. Batchelor. There are not many like him and although in principle one can do fancier experiments followed by modelling followed by very fancy computations — it is hard to imagine that any one being will be able to span it all as he did.
I turn next to Theodore von Karman born in 1881 in Hungary where he was trained as an engineer and when I claim him for applied mathematics it is because of the role he played in bringing mathematics into aeronautical engineering. In his autobiography he describes the poor engineering education he received and how he decided to study mechanics with Prandtl in Gottingen. But there he also studied mathematics and physics. He did some fundamental work with Born on crystal lattices but in the end went to Aachen as a professor of aeronautical engineering finally going to Caltech in 1930. Anybody who has studied flight or vortices or many other aspects of fluid dynamics knows von Karman’s work.
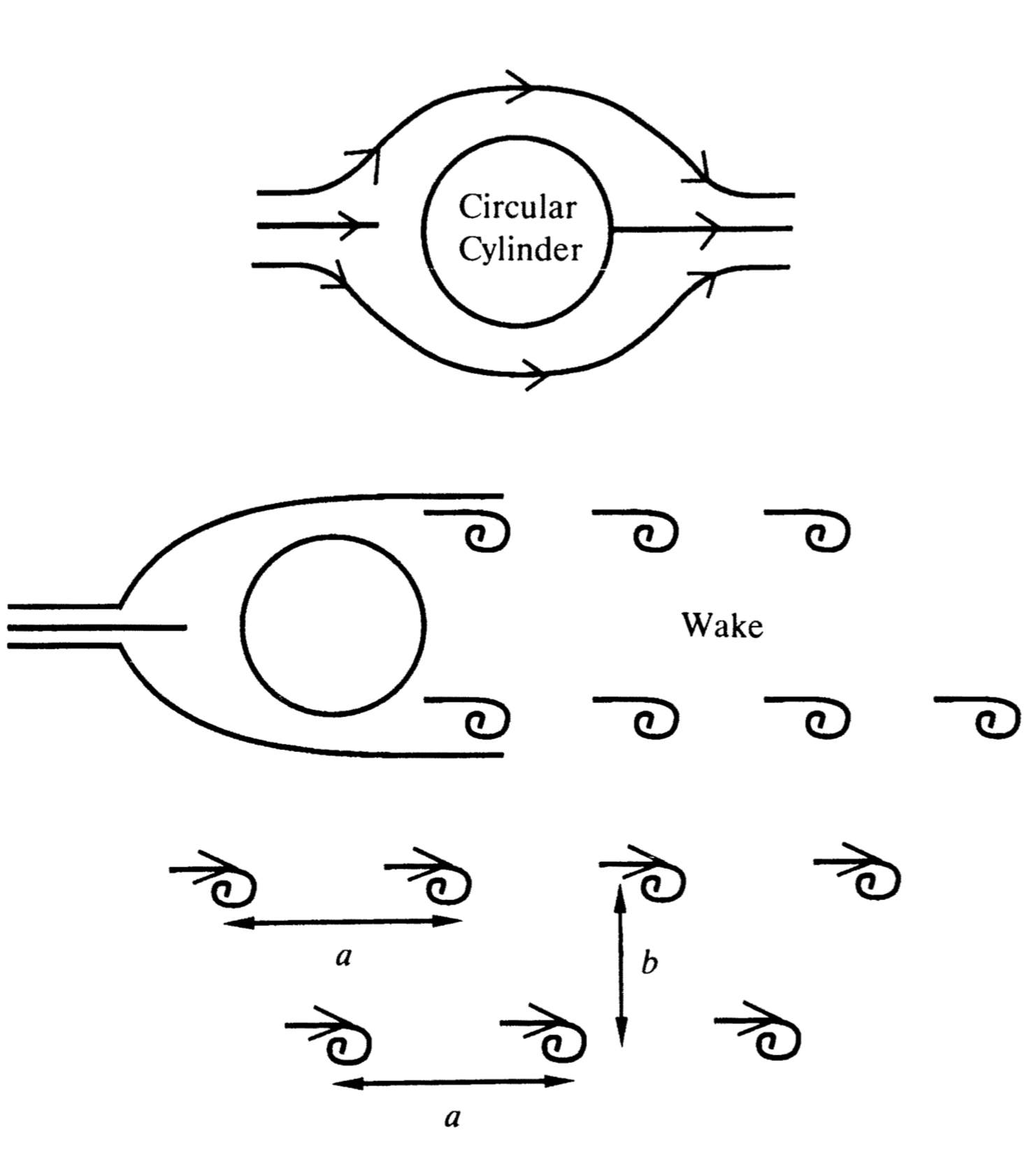
For example, I learned about the von Karman vortex street as an undergraduate in Toronto. It had been discovered by Hiemenz in Gottingen that no matter how smoothly a cylinder was honed to be circular, flow past it was always oscillatory and the cylinder oscillated too. One never found the classical 2D flow of the complex variable application, Figure 3a. Von Karman postulated that vortices were shed alternately on each side and a wave could not be avoided as in Figure 3b. He then proposed a simple model of a vortex street with regular spacings and equal strength vortices, Figure 3c.
He found the very elegant result that if the spacing and the width of the street do not satisfy a very simple ratio condition then the array is unstable.
Thus this pattern is the one that is seen. All others being unstable will not be seen.
Enamored by the elegance of this theory I wanted to go to Caltech myself but since Caltech did not admit women in 1945 I landed up in Wiener’s class at MIT instead. But I met von Karman later. I had written a paper on the so-called limiting line which had been a proposed way of explaining why most transonic flow has shocks. I attributed the idea to von Karman in part without checking a reference and then proceeded to show that it could not be the explanation. I was actually following up some work of Friedrichs. The next time von Karman came to N.Y. he invited Courant and Friedrichs, Lax as a representative Hungarian and me to lunch in his hotel. Every few minutes he turned to me and asked where I had seen the limiting line proposition. I felt terrible and learned my lesson but from then on was treated very well by von Karman.
His biggest role was as the father of our space program and the developer of rocketry. But wherever he could, he brought mathematics to bear. I think Friedrichs, or perhaps Courant told me that once when an admirer asked him about his successful mastery of a problem he patted a large pile of calculations meanwhile muttering “Physical intuition, physical intuition.”
Let me turn now to the “other kind” of a giant and let me begin with Norbert Wiener. Probably most of you have read his autobiography. There is no question that his formative years were his childhood years and that his tastes and ambitions were a product of his struggle to be independent of his father.
After graduating at the age of 14 from college, he tried graduate school in zoology but his clumsiness and bad eyesight made him realize that the experimental science of that time was not for him. He tried philosophy then logic and finally ended in mathematics. His enormous talent took time to develop and it was not until he had made many starts, that he settled down by his own account to really study mathematics at the age of 24. Finally, he was appointed to the faculty of MIT. In the late twenties he went for a second time as a young post-doc to Gottingen where his, I was going to say arrogance but perhaps it’s better to say his particular mixture of self-esteem and lack of self-esteem led Hilbert to try to “cure” him with scorn. The Hilbert entourage followed suit and Wiener understandably retained a lifelong dislike of many of them especially Richard Courant. When I told Wiener at a Sunday lunch at his house that I was leaving MIT to join Courant’s group as my new husband was in the New York area, I was not aware of this bad situation and couldn’t understand why Wiener refused to carry on the conversation. Thus, to say the least, I had very little contact with Wiener. But as a fresh graduate student I had briefly tried out his course in Noise and Random Processes. It was clearly for those who knew more mathematics than I had learned in Toronto in applied mathematics and I dropped out. In spite of the Gottingen story Wiener admired Hilbert and continued to see him as, to quote his autobiography, “the sort of mathematician I would like to become, combining tremendous abstract power with a down-to-earth sense of physical reality.”
To quote Mark Kac writing in 1964 on Wiener’s work:
“The simplest and most celebrated example of a stochastic process is the Brownian motion of a particle. Wiener conceived in (1921) the idea of basing the theory of Brownian motion on a theory of measure in a set of all continuous paths. This idea proved enormously fruitful for probability theory. It breathed new life into old problems.”
This work drew strongly on Taylor’s work that came from pictures of “plumes of smoke” and which had led Taylor to introduce his special correlations. As Norman Levinson put it there were two reasons for Wiener’s interest in Taylor’s work — one was that it inspired him to try turbulence as a model for his problem of integration in function spaces. And the other was that it suggested his own auto and cross correlation functions for his generalized harmonic analysis.
I reread the introduction to Wiener’s “Cybernetics.” Looked at from a human point of view one perceives the incredibly high scientific aspirations of Wiener. Resting, I would like to say comfortably (but even I knew as a student his uneasiness), on a long history of successful accomplishment Wiener wanted to conquer the brain with mathematics. In the course of it he worked very hard with able physicians and experts in neurology to become not only as knowledgable as he could but able to interact. His great ambition was to put together the extant knowledge of computers, feedback systems and physiology coupled with the emerging subject of signal processing — all subjects he had contributed to fundamentally. The course I went to in 1945 was a spinoff of these interests.
In his introduction, read now 43 years later, he takes a rather high position for the role of his new subject. Still cybernetics has stood the test of time with engineers. His view of the relation of science and society is interesting if pessimistic.
“The best we can do is to see that a large public understands the trend and the bearing of the present work, and to confine our personal efforts to those fields, such as physiology and psychology, most remote from war and exploitation. As we have seen, there are those who hope that the good of a better understanding of man and society which is offered by this new field of work may anticipate and outweigh the incidental contribution we are making to the concentration of power (which is always concentrated, by its very conditions of existence, in the hands of the most unscrupulous). I write in 1947, and I am compelled to say that it is a very slight hope.”
There is no good source of biographical information for my next giant, John von Neumann. This situation is being repaired and we can look forward to a full biography in the next couple of years. v. Neumann was, like Wiener, a mathematical prodigy as a child. His father, however, was an enlightened banker and somehow or other when v. Neumann was ready to go to university a compromise between banking (big business) and mathematics (purest of sciences) was worked out. v. Neumann went to Zurich to study chemistry (possibly applicable in the eyes of the family).
I never met von Neumann. Occasionally I saw him in Richard Courant’s company. And that affected my life a lot because as I understand it, it was at v. Neumann’s recommendation that the first big university computer was placed with Courant’s group at N.Y.U. That was probably not disconnected from the fact that Courant and those around him shared v. Neumann’s view that mathematics would become an arid subject if it lost contact with science and engineering.
Those who knew v. Neumann always remark on the speed of his brain. He grasped things immediately. His interests ranged over everything. I don’t know whether one should call his early work in quantum mechanics applied. One might say he set it up as a part of pure mathematics. His early elegant work in game theory received little attention until after the Second World War. But even before the Second World War broke out he became involved in ballistics in anticipation.
von Neumann, as everyone knows played a big role in the development of the atomic bomb. And it was in that connection that he made his mark in fluid dynamics.
Despite some striking contributions to the field (lots of us are hard at work these days on the paradoxes he uncovered in shock reflection) it led him quickly into big computation (big for its day) and hence into the whole area of large scale computing: The universal machine, the coding, the programming. Some ideas were around but he cleaned them up and set the whole thing on a logical and expandable footing. As Peter Lax has suggested he would have developed parallel computing if he had lived long enough. I have really no time to bring up his many contributions, to economics, to Monte Carlo methods etc. It might be said of v. Neumann that his sweep was so broad that it included most of applied mathematics.
I would only like to reiterate his philosophy that mathematics would become an esoteric arid branch of science if it lost its connections. I think he would be happy to see today how modern mathematics is knitting bonds within its many branches and even more with other sciences.
I turn now to my teacher Kurt Friedrichs, or as he was known to those around him, Frieder.
Born in Kiel in 1901 he entered university in Dusseldorf. Following the German practice he studied a variety of topics in a variety of places (including the philosophy of Husserl and Heidegger). Finally, he came to “the Mecca of mathematics,” Gottingen in 1922.
His relation to mathematics, pure and applied, is best described by his own expression that “he was like a dancing bear on a stove, first hopping on his pure foot till it got too hot and then on his applied foot.” In fact, if one looks over his work one finds a pretty random distribution. His first official applied mathematical work was as von Karman’s assistant in Aachen. He took the position according to his own explanation to Constance Reed because Courant thought that in the late twenties Friedrichs being so shy and withdrawn would have a hard time competing against pure mathematicians for an academic position in Germany. He became shortly the youngest professor at the University of Braunschweig. He left Germany to join Courant in America partly from disgust with the Nazis but also to be able to marry Nellie Bruell, forbidden under the Nazi racist rules.
From then on he worked in elasticity, fluid dynamics, quantum field theory, plasma physics alternately with partial differential equations, asymptotics, spectral theory and other subjects too pure to be applied but too applied to be quite pure. Friedrichs liked to say that applied mathematics was whatever the physicist had discarded as no longer exciting.
As a graduate student at New York University I first worked at editing the book on “Supersonic Flow and Shock Waves” by Courant and Friedrichs. That was my good luck. I learned the main ideas from Courant and the exceptions and the necessity to be accurate from Friedrichs.
After passing my orals after my first child I went to Friedrichs for a thesis topic. I thought it would be in fluid dynamics but he showed me a whole bunch of topics mainly I think on spectral theory. He asked me if I could get excited about one; that was an essential part of my taking it on. I could not but we agreed I would work on one. But when my second child was on the way, the gods (Courant, Stoker and Friedrichs) decided my contract work could be developed quickly into a thesis. It was on stability of implosions (used as neither I nor Friedrichs knew for detonating the atomic bomb. It was connected to the collapse of supernovae under self-gravitation.) Beautiful special solutions can be found using the group invariance of the equations. Friedrichs was hopping on his pure foot and at times it was very hard to get him to think about fluids. Incidentally the idea of an implosion had been considered by v. Neumann, G. I. Taylor and by the German aeronautical scientist Guderley and for all I know the Russians. My stability result was very modest but it did give me a thesis and the asymptotic theory involved gave me a good start for other problems. I kept on learning from Friedrichs but I never did get involved in either quantum mechanics or spectral theory.
Once Friedrichs got a physical problem properly and clearly mathematized (as say with either fluid dynamics or magneto-hydrodynamics), he then went after it with every tool he knew and wrestled it to the ground. When I was helping him with his Selecta just a few years before he died he kept saying “oh let’s not pick that one. So and so did it much more cleanly later.” He somehow had trouble realizing how important his innovations had been.
One of the things that surprised me about Friedrichs was his indifference to the role of the big computer and even his own contributions to difference schemes as a useful tool for finding answers as opposed to existence theorems. I tried once to draw him out on that subject but got nowhere — which is the way it was when Friedrichs did not want to follow a particular line of thought. I wish now that I had asked him a lot more.

My father is another example of the applied mathematician of this century. Born in 1897 and trained in Trinity College Dublin he came to Canada as a young man and started working in mechanics. He was diverted into differential geometry and the exciting new subject of relativity by the influence of Veblen. His lifelong interest was in the intersection of geometry and physics. He was fascinated like Taylor at the way nature worked and he fought hard for the turf of applied mathematics through the thirties. The war threw a lot of mathematicians into applied problems (in Canada that was 1939) and he fitted naturally. None of us should forget how frightened our world was at the thought that Hitler would win and his terrible ideas would prevail. Today some may look back and ask how we could have helped with weapons of destruction. But by and large there was very little pacifism and applied mathematicians for the most part were heavily engaged. It was in that period I first studied mathematics and its utility was of paramount interest. Only later did I capture the sense from my father of the beauty of nature transformed into mathematics and from Friedrichs the beauty of proof of the resulting mathematics.
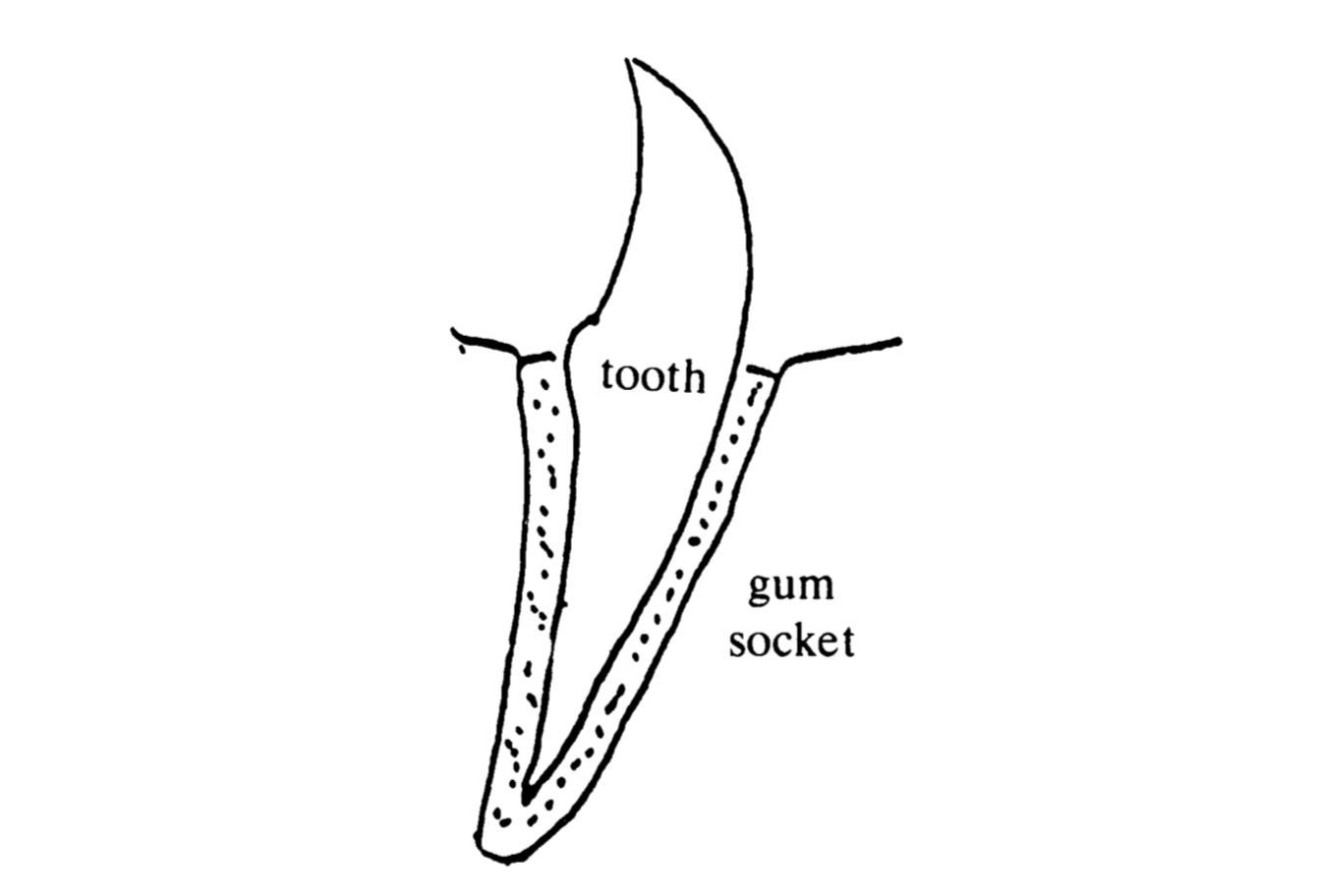
My father’s work has ranged from ideal steering mechanisms to general relativity with the latter being his main stomping ground. A particular physics-geometry approach led him to invent the first finite element method accompanied by estimates. But the item I would like to tell you about is his excursion into dentistry and his feelings about it, since they have a universal application. In the thirties he was approached by a dentist, H. K. Box, about the problem of traumatic occlusion caused by biting. What’s that? In Figure 4, we have a rigid tooth lying in its rigid socket and separated from each other by the periodontal membrane which is transmitting the force of the bite and also the pain of traumatic occlusion if the membrane defects. Clearly a problem in elasticity and, mindful of George Bernard Shaw’s saying that even the Archbishop of Canterbury is 90% water, my father decided to tackle the problem with a model of a thin incompressible elastic membrane to represent the periodontal membrane. He worked hard and got some results but in 1972, 40 years later when he received the Boyle medal in Dublin he reflected:
“I have a social conscience of sorts. When Dr. Box told me about traumatic occlusion, I lacked the strength of mind to tell him that I had other things to do. So I engaged on this work as a social duty. But as the mathematical argument took shape, my professionalism took over and I was fascinated by this problem in which the geometry of the tooth and the physics of the membrane were combined. The final result calls for a sardonic laugh. On the one hand, you have a paper of over forty pages, published nearly forty years ago, full of intricate formulae developed (if I may say so) with considerable skill. On the other hand, you have humanity suffering still, I presume, from traumatic occlusion.”
So one must be wary of trying to do good in mathematics.
I’d like to close with a parting shot in the dark. Of all the sciences mathematics has had the least impact on biology. v. Neumann died before the spectacular developments of molecular biology had started and that is really even true of Wiener. Both were challenged by problems of biology but as it turned out somewhat peripheral problems. Can we look forward in the next decade to new giants: to a new G. I. Taylor or a new von Karman thoroughly immersed in biology as they were in mechanics who will bring to the v. Neumann or Wiener of the day the deep and as yet not formulated mathematical problems of biology? I think that’s an extremely interesting future to look forward to.
Thank you.