by Constance Reid
Introduction
It was my sister Julia Robinson who first suggested to me that I wrote the lives of mathematicians. She thought that students would be interested in knowing something about the people whose names are attached to theorems and concepts in textbooks. She herself, in the normal course of events, would never have considered recounting the story of her own life. As far as she was concerned, what she had done mathematically was all that was significant. However, with her acceptance in 1982 of a public role as president of the American Mathematical Society, she found this position increasingly untenable. She also came under pressure from the society and various academies for official biographical material. Finally one day she said, “Constance, you write something!”
That was late in the spring of 1985 when we were bicycling at Pebble Beach. The preceding August, during the summer meeting of the AMS at Eugene, she had learned that she had leukemia. After lengthy treatment by chemotherapy, she had finally won a remission from the disease. At Pebble Beach she said that she felt as good as she ever had.
I could never write about Julia without writing more intimately then she or I would wish, and it took me a while to come up with the solution of writing her “autobiography.” What I wrote would then be entirely what she would want to have written about her own life. I would be writing in her spirit, not my own. She was amused by the idea and agreeable, although not completely reconciled. Later she happened upon something by the writer Kay Boyle to the effect that the only excuse for writing an autobiography is to give credit where credit has not been given. That seemed to her a reasonable justification, for there were people to whom she very much wanted to give credit.
Just a few weeks after we were bicycling at Pebble Beach, she learned that her hard-won remission had ended. When I started to write, she was back in the hospital. Although she was hopeful of a second remission, she was also realistic about her chances. Every few days I read aloud to her what I had written. She listened attentively and amended or deleted as appropriate, sometimes just a word. She heard and approved all that which appears below — although she objected that my account of her life was much too long. Her own life was not. She died on July 30, 1985, at the age of sixty-five.
\[ \star\qquad\star\qquad\star \]

I was born in St. Louis, Missouri, on December 8, 1919, the second of two daughters born to Ralph Bowers Bowman and Helen Hall Bowman. Neither of my parents had gone to college, but both had had good secondary educations and my mother had gone to business college after graduation from high school. I learned recently from her commencement program that in high school she had elected to follow the scientific course rather than the more popular liberal arts course.
My mother died when I was two, and my father sent my sister, Constance, and me with our nurse to Arizona, where our grandmother wintered for her health. We lived 12 miles from Phoenix in the middle of the desert, very close to Camelback Mountain. Ours was a tiny community of only three or four families living under quite primitive conditions.
After my mother’s death my father, who was the owner of a machine tool and equipment company, lost interest in his business. He had saved what was an enormous sum in those days; and he was certain that, conservatively invested, it would provide an income sufficient to support his family. When he remarried, he closed his office and joined us in Arizona. My new mother had been Edenia Kridelbaugh before her marriage. Subsequently I shall refer to her as my mother, for I always thought of her that way.
We continued to live in Arizona for several years. One of my earliest memories is of arranging pebbles in the shadow of a giant saguaro, squinting because the sun was so bright. I thought that I have always had a basic liking for the natural numbers. To me they are the one real thing. We can conceive of a chemistry which is different from ours, or a biology, but we cannot conceive of a different mathematics of numbers. What is proved about numbers will be a fact in any universe.
I was slow to talk and pronounced the words so oddly that no one except Constance could understand me. Since people would ask me a question and look at Constance for the answer, she got into the habit of speaking for me, and she is now. My mother, who had taught kindergarten and first grade before her marriage, said that I was the stubbornnest child she had ever known. I would say that my stubbornness has been to a great extent responsible for whatever success I have had in mathematics. But then it is a common trait among mathematicians.
Our family always left Arizona during the summer. Several times we went to San Diego; and in 1925, when I was five and Constance seven, my mother, who had been teaching Constance at home, insisted that my father settle someplace where we could go to school. That fall we moved to Point Loma on San Diego Bay.
Except for the fort and the lighthouse, which are still there, Point Loma was at the time quite different from the expensive, overbuilt residential area which it is today. There were about fifty families scattered over the hill, not counting the military families at Fort Rosecrans or the colony of Portuguese fisherman. Like the desert, it was open to exploration and fantasy.
The Cabrillo Elementary School which we attended was very small with several grades combined in each classroom. During our first few years both Constance and I were skipped so that later we were always among the youngest in our classes.
The most exciting event of our first years on Point Loma was the birth of our little sister, Billie, on Easter Sunday at 1928. It was followed by an event which was to have a permanent effect upon my life and career.
Less than a year after Billie’s birth, when I was nine years old, I came down with scarlet fever. To prevent the spread of the disease, especially to the new baby, my father took over my care. He washed all my dishes and, whenever he entered my room, put on an old duster which he had worn when we had an open touring car. The entire family was isolated and a conspicuous sign to that effect posted on the front door. When, after a month, the isolation was lifted, the family celebrated by going to see “The Ghost Speaks.” I believe it was our first “talkie.”

The scarlet fever was followed by rheumatic fever, which today would be treated effectively with penicillin. My family moved from Point Loma so that I would not find myself in a class behind my old classmates when I went back to school, but I did not recover as soon as expected. Ultimately I had to spend a year in bed at the home of a practical nurse. During that year there was nothing in the world which I wanted so much as a bicycle. My father assured me that when I got well I would get one but, childlike, I interpreted this as meaning that I was not going to get well.
I have since read that a solitary childhood or, what amounts to the same thing, a period of isolation resulting from illness is frequently noted in the early lives of scientists. I am not sure what the significance of this finding is. Obviously I had to amuse myself for long periods of time, but I didn’t do so with mathematics. I am inclined to think that what I learned during that year in bed was patience.
By the time I was well enough to go back to school, I had missed more than two years. My parents arranged to have me tutored by a retired elementary school teacher. In one year, working three mornings a week, she and I went through the state syllabuses for the fifth, sixth, seventh, and eighth grades. It makes me wonder how much time must be wasted in classrooms. One day she told me that you could never carry the square root of two to a point where the decimal begin to repeat. She knew that this fact had been proved, although she did not know how. I didn’t see how anyone could prove such a thing, and I went home and utilized my newly acquired skills at extracting square roots to check it but finally, late in the afternoon, gave up.

In the fall of 1932, a few months before the election of Franklin Roosevelt, I entered the ninth grade at Theodore Roosevelt Junior High School. For me it was an almost Kafka-like experience. I was a beginner in the game which everyone else in my class have been playing for two years. I made many stupid and embarrassing mistakes and ate lunch in a corner as quickly as I could so that no one would notice that I was alone. Finally a girl named Virginia Bell invited me to eat with her and her friends. She became my best and only friend as long as I remained in San Diego. A few years ago, when I returned for a colloquium lecture there, I visited her and found that although much had happened to us both in the interim we were still just as congenial as we had been during our school days.
At Roosevelt I was introduced to algebra by a woman mathematics teacher. Before graduation she made a valiant effort to explain to the class that sometimes the best students in math could not get math honors because they had not received grades at their previous school.
The mathematics course at San Diego High School was standard for that time: plane geometry in the tenth grade, advanced algebra in the eleventh, and trigonometry and solid geometry in the twelfth. There were two women mathematics teachers, and I took classes from both of them. After plane geometry (which fulfilled the University of California’s entrance requirement), I was the only girl still taking mathematics. I was also the only girl in physics. I was very shy so it may sound strange for me to say that entering a room full of boys did not disconcert me. Unlike many shy people I have never given much thought to what other people think about me. I believe this attitude is a legacy from my parents. My father conveyed it by example, but my mother frequently articulated it to us. Naturally I was interested in some of the boys in my math classes, but they didn’t pay any attention to me except when they had a question about the homework. None of them ever seem to be bothered by the fact that a girl was getting the best grades.
My high school mathematics teachers were all well qualified to teach the subject at that level — unlike the high school teacher my nephew later had who always referred to “the communicative laws of arithmetic.” There were, however, no enrichment programs in the high schools in the 1930s, no math days at the local college, no well publicized competitions like the Putnam. None of my teachers encouraged me to do more advanced work. Of course I did try a few of the usual things like trisecting the angle. Once — and this is just about the only piece of personal direction that I recall — one of my teachers, it may have been the head of the department, who was my counselor, advised me that now that I had learned to solve math problems I should learn to be neat.
We had all been given an intelligence test — I think it was the Otis — while we were still in junior high school. Constance had done very well on it but I, being a slower reader and unaccustomed to taking tests, had done poorly. She found out later, when she was herself a teacher at the high school, that my I.Q. was recorded as 98, two points below average. The result was that even after we were in college, Constance, who took her classes lightly while devoting herself to the school paper, was being called into the office to find out why she wasn’t doing better while I was being called in to find out why I was able to perform above ability.

My friend Virginia Bell was an art major — she later became an art teacher and supervisor in the San Diego City Schools — and, encouraged by her and by the fact that one semester of art or music was a requirement, I took an art course in which I learned something about perspective and among other things drew an impressively realistic baseball. I was a great baseball fan, keeping box scores at games and spending my allowance on The Sporting News. In spite of my complete lack of musical ability or appreciation, I had a crush on the Metropolitan Opera’s baritone, Lawrence Tibbett, who starred in several movies at that time. When he gave a concert in San Diego, my mother got tickets for us; and my father, an inveterate photographer, took a picture for me of the billboard advertising the concert. I learned from my father how to shoot both a rifle and a pistol and once wrote a paper on barrel rifling for physics. I mentioned these things only to show that I was not absorbed entirely in mathematics.
In retrospect, I see my high school years as very relaxed compared to those of young people today. There was no pressure to get into a “good” college, and my parents were seemingly unconcerned by the fact that on occasion I was in an English class which was not college preparatory. They were concerned, though, that I had only one friend and didn’t seem to know how to make any others.

Of course, since we were still in the middle of the Depression, I was always conscious of economic pressures. My fathers savings were being eroded more rapidly than any of us dreamed. He listened every noon to the stock market report, and his mood for the next 24 hours depended on whether the market had gone up or down. We never went without anything essential, but we had no luxuries such as trips during summer vacations. I remember that our next-door neighbor, a civil engineer, lost his job and began to make jigsaw puzzles, which along with Monopoly had become a national fad.
When I graduated from high school, I received awards in mathematics and the other sciences I had taken as well as the Bausch–Lomb medal for all-around excellence in science. My selection for this last was not approved by some of the science teachers because I had never taken chemistry, the subject which to this day I know nothing about. After the award assembly my mother expressed some concern about what the future could hold for such a girl, but my father told her not to worry — I would marry a professor. My graduation present was a beautiful and expensive slide rule, which I christened “Slippy.”
It had always been taken for granted that Constance and I would go to college. That meant the local state college (now San Diego State University). State, as it was called, had been until quite recently a teachers’ college and, before that, a normal school. Very few of my high school classmates went away to college after graduation, but a number attended State for two years and then transferred to UC or UCLA. Those who remained took some education courses and got one of the several teaching credentials which were offered. My mother had always inculcated in us the idea that a girl should equip herself to earn a living. She placed an especially high value on a teaching credential because it qualified the holder to do a very specific thing for which she would be paid.
At State there were only a few PhD’s on the faculty. Neither of the two mathematics professors had a doctorate. There were no women teaching mathematics; but I remember women, with doctorates, teaching biology and psychology.
Naturally I elected to major in mathematics. The lower division majors followed the usual sequence of courses in analytic geometry and calculus. There were 35 or 40 math students, most of them planning to be engineers, so there was some competition. There were also girls who were going to be teachers. At that time I had no idea that such a thing as a mathematician (as opposed to a math teacher) existed.
By the beginning of my sophomore year all the savings which my father had so confidently expected to support his retirement had been wiped out. He took his own life that September, leaving behind only an insurance policy on which he had borrowed to the limit and an unimproved lot on Point Loma. We moved to a modest apartment and received some regular financial help from our aunt, Lucille Hall, an elementary school teacher in St. Louis. In spite of our straightened circumstances, Constance and I continued in college. Tuition at that time was \$12 a semester.
In the upper division at State the number of math students dropped precipitously, those who were going to be engineers having transferred to other colleges. Two, and only two, upper division mathematics courses were offered each semester. All the math majors had to take them. In a way this was a good system because we focused on those two in a way we wouldn’t have if there had been a larger number of courses offered. In my junior year I took advanced calculus, which completed the calculus cycle although it wasn’t so advanced as Math 104 (real analysis) at Berkeley. I also took a course in algebra that was the equivalent of Math 8, a lower division course at Berkeley. There was something called modern geometry, which was really very old-fashioned (nothing nonEuclidean). The history of mathematics was also offered. It was probably in that class that I read E. T. Bell’s Men of Mathematics, which had just been published.
Mathematics was by far my favorite subject, but I hardly knew what the subject was. The only idea of real mathematics which I had came from Men of Mathematics. In it I got my first glimpse of a mathematician per se. I cannot overemphasize the importance of such books about mathematics in the intellectual life of a student like myself completely out of contact with research mathematicians. I learned many interesting things from Bell’s book. I was especially excited by some of the theorems of number theory — he was a number theorist himself — and I used to recount these to Constance at night after we went to bed. She soon found that if she wasn’t ready to go to sleep she could keep me awake by asking questions about mathematics.
Neither Constance nor I was interested in teaching elementary school or qualified to get one of the special credentials offered in art, music, or physical education. We settled reluctantly on the very limited junior high school credential. I took some of the required education courses and found them boring. Also, when Constance graduated, I learned that a junior high school credential did not guarantee a teaching job. It was not highly regarded by school superintendents, who could get teachers with the more comprehensive general secondary credential for the same salary. To obtain such a credential, however, you had to take a post-graduation year on one of the campuses of the University of California.
When, six months after graduation, Constance still had no job, my mother, with great courage and faith in the future, dug into the family’s small savings and sent her to Berkeley. Happily the gamble paid off. Even before Constance had finished the coursework for the new credential, she was hired as an English/Journalism teacher and faculty adviser of the school paper at San Diego High School.
I now conceived an absolute passion to go away to school, too — whether to UC or UCLA, I was not particular — any place where there was a real department of mathematics. A young PhD in astronomy from Berkeley, Clifford E. Smith, had joined the faculty at State; and although I don’t remember his encouraging me to go away, he did give me a glimpse of something beyond Mr. Livingston and Mr. Gleason. I am sure he found the students at State quite a change from the politically conscious students at Berkeley. One morning he announced that we were excused from turning in our homework because he knew that we had been up late the night before listening to the radio. We looked bewilderedly at one another, none of us aware that Chamberlain and Hitler had just come to an agreement in Munich which would still, almost 50 years later, symbolize appeasement and dishonor.
When, after Constance had her job, I told the math professors at State that I was going to go somewhere else the following year, Mr. Livingston, the head of the department, tried to dissuade me. The college was planning to inaugurate an honors program, and I was obviously the only mathematics student whom he could propose. Mr. Gleason, however, said that I should go and that I should go to Berkeley rather than UCLA.
I arrived at Berkeley most fortuitously as far as mathematics was concerned, although of course I did not realize it then. At the beginning of the 1930s the other science departments had persuaded President Sproul to bring in someone of recognized achievement to head the mathematics department and upgrade it. The mathematician who had been chosen was Griffith C. Evans. He had almost immediately hired Alfred Foster, Charles Morrey, and Hans Lewy. The year before I arrived he had brought Jerzy Neyman from England.
My mother expected me to get a general secondary credential, just as Constance had; but the adviser for math majors planning to go into teaching discouraged me. I never understood why, but Constance tells me that although there were a number of women teaching mathematics in junior and senior high schools, as I have indicated, there was a definite drive (affirmative action?) to bring more men into secondary education and it was thought this could be done most easily in the sciences.
I took five courses in mathematics that first year at Berkeley, including a course in number theory taught by Raphael M. Robinson. The fact that Raphael was teaching number theory was a stroke of luck — for us. Evans had hired Dick Lehmer as the department’s number theory specialist, but Dick had had to fulfill a year’s commitment to Lehigh before he could come to Berkeley and Raphael had been assigned to teach number theory in his place. In the second semester there were only four students — I was again the only girl — and Raphael began to ask me to go on walks with him.
Although I had lost some credits by transferring, I was still able to get my A.B. in a year. I applied for jobs with various companies in San Francisco, but they were not interested in my mathematical training — they asked if I could type. (A few years later, after we were in the war, they suddenly did become interested in me.) I applied to Evans for a teaching assistantship, but he was trying to bring students from other universities to Berkeley. He told me that the only possible position for me was at Oregon State. Since it was an undergraduate department and I would not be able to go on with my studies, he advised me not to take it. Neyman, hearing of my plight, quickly arranged for me to get some of the money which had been allotted for Betty Scott, his half-time lab assistant. As I remember, she wanted a little more time for her studies anyway — she was an astronomy major then, now of course a long-time professor of statistics at Berkeley — so she took two-thirds of the half and I took the other one-third. I remember that Neyman asked me how much I needed to live on. I said \$32 a month and he got me \$35.
I was very happy, really blissfully happy, at Berkeley. In San Diego there had been no one at all like me. If, as Bruno Bettelheim has said, everyone has his or her own fairy story, mine is the story of the ugly duckling. Suddenly, at Berkeley, I found that I was really a swan. There were lots of people, students as well as faculty members, just as excited as I was about mathematics. I was elected to the honorary mathematics fraternity, and there was quite a bit of departmental social activity in which I was included. Then there was Raphael.
During our increasingly frequent walks, he told me about various interesting things in mathematics. He is, in my opinion, a very good teacher. He thoroughly understands a large part of mathematics, both classical and modern, and has it so well organized in his mind that he is able to explain it with exceptional clarity. On one of our early walks, he introduced me to Gödel’s results. I was very impressed and excited by the fact that things about numbers could be proved by symbolic logic. Without question what had the greatest mathematical impact on me at Berkeley was the one-to-one teaching that I received from Raphael.
Although I had done well in mathematics, my mother was concerned about my getting a real job and earning some real money. Earlier, I had taken a civil service examination for Junior Statistician; now I was offered a job as a night clerk in Washington DC at \$1200 a year. My mother thought that I should except it, but Raphael had other ideas. At his insistence I came back to Berkeley for a second graduate year and, this time, received a teaching assistantship. I wanted to teach calculus, but Neyman asked Evans for me and so I taught statistics (which I found very messy, not beautiful and clear and true like number theory). At the end of the semester, a few weeks after the Japanese attacked Pearl Harbor, Raphael and I were married.
Mina Rees has observed that it is hard to name a woman mathematician who isn’t married to a man mathematician. I think what she says was very true in her generation and also in mine, although no longer true. I doubt that I would have become a mathematician if it hadn’t been for Raphael. He taught me and has continued to teach me, has encouraged me, and has supported me in many ways, including financially. Through his position as a professor at Berkeley, he has provided me with access to professional facilities and society. Although he is a much better and much brighter mathematician than I, his research is not so generally appreciated, since he has pursued his own interests rather than current fashions or flashy problems. He keeps up with modern developments even now in his 70s, working through the recent proof of the Bieberbach conjecture, for example; but he has always been a rather old fashion mathematician — as he says, he has liked to work on “neglected problems.” I feel that his work is very interesting and should be much better known, and I am planning to take it as the subject of my Presidential Address at the AMS meeting in New Orleans this winter.
When we were married, there was a rule at Berkeley that members of the same family could not teach in the same department. Since I already had a one-year contract as a teaching assistant, this rule did not immediately apply to me. I didn’t really like teaching statistics, especially since Neyman, convinced that American students were woefully ignorant of statistical theory, had conceived the idea of using both lecture and lab for lectures and making the students do the lab work on their own time. I wrote and asked Evans if I could teach mathematics instead. He did not respond, but Neyman heard about my letter and became very angry. He stop using me as a T.A. and left me in a kind of limbo for the rest of the academic year, doing absolutely nothing for the money I was regularly being paid. He did not hold a grudge, however. During the war he employed me in the stat lab, and my first paper came out of the stat lab work. Actually I did not want to publish it because someone else had already proved the same thing, although in a different way; but Neyman insisted. (He always encouraged students to publish before they got their degrees.) For many years I avoided him because I found it almost impossible to say no to him, but I understand that when I was proposed for membership in the National Academy of Sciences he was one of my most enthusiastic and energetic supporters.

Because of the nepotism rule I could not teach in the mathematics department the next year, but this fact did not particularly concern me. Now that I was married, I expected and very much wanted to have a family. Raphael and I bought a house and, although I continued to audit math courses, I was really more interested in shopping for furniture. When I finally learned that I was pregnant, I was delighted — and very disappointed when a few months later I lost the baby. Shortly afterwards, visiting in San Diego, I contracted viral pneumonia. My mother called a doctor. His first question after he examined me was, “how long have you had heart trouble?” It was true that I had always puffed, especially climbing the stairs to the math classes on the third floor of Wheeler Hall (only professors were permitted to use the elevator in those days); but no one, including my obstetrician, had ever shown more than a cursory interest in the condition of my heart. I believe the doctor in San Diego had had rheumatic fever himself and was thus more familiar with the resulting buildup of scar tissue in the mitral valve. He advised me that under no circumstances should I become pregnant again and told my mother privately that I would probably be dead by forty, since by that time my heart would have broken down completely. What he could not know was that when I was forty-one a surgeon would be able to go into the mitral valve and remove the scar tissue!
For a long time I was deeply depressed by the fact that we could not have children. Finally Raphael reminded me that there was still mathematics. He had written a paper about simplifying definitions of primitive recursive functions, and he suggested that I do the same thing for general recursive functions. I worked very hard on the problem during the year 1946–47, when we were at Princeton, and published my results the following year. I cannot honestly say that the mathematical problem eliminated the emotional problem, but it did help to take my mind off it some of the time. When we came back to Berkeley, I began to work toward a PhD with Alfred Tarski.
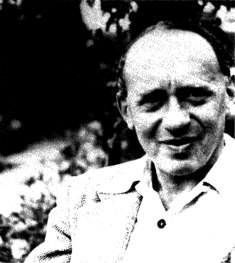
Tarski, a Pole, had been caught in the United States, as a visiting lecturer at Harvard, when Germany invaded Poland in 1939. Unbelievable as it now seems, a permanent position had not been found for him between 1939 and 1942, when Evans brought him to Berkeley. Like Neyman, Tarski was a tremendous addition to our department. In my opinion, and that of many other people, he ranks with Gödel as a logician.
Previously, in the summer of 1943, I had audited a seminar given by Tarski on Gödel’s results. In the summer he had read us a letter from Mostowski, who had been his only Polish PhD. Mostowski wanted to know whether it was possible to define addition in terms of successor and multiplication. I played around with the problem and in a couple of days came up with a very complicated definition. It is still rather surprising to me that I was able to do this, considering the low probability of a mathematician’s going directly to a definition. Tarski was immensely pleased and made some remark to the fact that my work was so original that it would do for a thesis. In writing up my results, however, I kept generalizing and simplifying it until it became essentially trivial. I knew without Tarski’s telling me that it wasn’t enough for a thesis. Later he suggested a problem about relation algebra. I never really got anywhere with it or maybe just didn’t work very hard, since I wasn’t particularly interested in it.
Tarski had great respect for Raphael and often talked with him about problems. One day at lunch at the Men’s Faculty Club (in those days women were not allowed in the main dining room at lunch), he mentioned the question whether one could give a first order definition of the integers in the field of rationals. This was not meant as a suggestion for a thesis topic for me; but when Raphael came home, he told me about it. I found it interesting, and I just began to work on it without saying anything to Tarski. I think that a great deal of the difficulty that students have in producing a thesis goes back to the fact that they are not really interested in the problem that they are given, just as I was not interested in Tarski’s problem about relation algebra. I consider myself very lucky to have come so early upon a field and a problem that excited me.
In my thesis, “Definability and decision problems in arithmetic” [1], I showed that the notion of an integer can be defined arithmetically in terms of the notion of a rational number and the operations of addition and multiplication on rationals. Thus the arithmetic of rationals is adequate for the formulation of all problems of elementary number theory. Since the solution of the decision problem was already known to be negative for elementary number theory, it followed from my results that the solution of the decision problem is negative for the theory of rationals. When I took my work to Tarski, he was delighted. It was then that he told me that he had been concerned that the other thing had become so simple, although it is still included in my thesis.
Tarski had always recognized that the decision problem for the theory of arbitrary fields would be undecidable if the integers could be defined in the field of rationals. That was why he had been interested in the problem in the first place. So he added a section to my thesis pointing out that undecidability for arbitrary fields follows from my work. I always gave him the credit for that result, since he was the one who recognized it; but he always gave me the credit, since he had not been able to establish it himself. Later somebody produced a simpler and more direct proof for a different field, but I don’t believe that anyone has improved on my work on definability in the rational field.
Tarski was a very inspiring teacher. He had a way of setting results into a framework so that they all fit nicely together, and he was always full of problems — he just bubbled over with problems. There are teachers whose lectures are so well organized that they convey the impression that mathematics is absolutely finished. Tarski’s lectures were equally well organized; but, because of the problems, you knew that there were still things that even you could do which would make for progress. Often, of course, he had problems which he didn’t give to students because he thought they were too hard; and sometimes he was mistaken about what was an easy problem. Bob Vaught once went to him, terribly depressed because he felt that he hadn’t been able to accomplish anything in mathematics. He asked for an easy problem that he was sure to be able to solve, and Tarski gave him this problem — it’s still unsolved! Fortunately Bob went on with mathematics anyway.
In 1948, the same year that I got my PhD, I began to work on the tenth problem on Hilbert’s famous list: to find an effective method for determining if a given Diophantine equation is solvable in integers. This problem has occupied the largest portion of my professional career. Again it was Tarski, talking to Raphael, who started me off. He had noticed that the numbers which are not powers of two can be existentially defined as the solution of a Diophantine equation. One simply has to show that the number contains an odd factor; for example, \( z \) is not a power of 2 if and only if there exist integers \( x \) and \( y \) such that \( z=(2x+3)y \). He wondered whether, possibly using induction, one could prove that the powers of 2 cannot be put in the form of a solution of a Diophantine equation.
Again Raphael mentioned the problem to me when he came home. I am sure that Tarski was thinking about the Tenth Problem, but I wasn’t — in the beginning. Probably if I had been, I would never have tackled it. I was just thinking about that specific problem. It was a problem that was not of particular interest in itself; however, it appealed to me. I like to work on that type of problem. Usually in mathematics you have an equation and you want to find a solution. Here you were given a solution and you had to find the equation. I liked that. I would have worked on the problem very hard without the connection to the Tenth Problem, but soon it became clear to me that that was where it came from. I haven’t worked on very many problems, and the ones that I have worked on have been problems that I find interesting even when I recognize that they would not be so interesting to other people. That is partly because I’ve never been held to getting results and publishing or perishing. As Raphael says, the problem of over-production of mathematics would be solved if we just changed the or to and.
I wasn’t able to show that the powers of 2 cannot be expressed as the solution of a Diophantine equation. In fact, I became discouraged right away, because proving something by induction over polynomials, as Tarski had suggested, is very difficult. Instead I started to work in the other direction, trying to prove that powers of 2 like nonpowers of 2 could be so expressed. When I couldn’t do that either, I turned to related problems of existential definability. The relevance of my efforts to Hilbert’s problem is clear from the fact that a set of natural numbers is existentially definable if and only if it is the set of values of a parameter for which a certain Diophantine equation is solvable. The main result in my paper, “Existential definability in arithmetic” [3], was the proof that the relation \( x=y^2 \) is existentially definable in terms of any relation of roughly exponential growth.
Raphael had a sabbatical coming up in 1949–50. Since I had had virtually no teaching experience, I wanted to teach at UCLA that year. As it turned out, Oliver Gross was there, and he was interested in George Brown’s fictitious play problem, which had been proposed as a means of computing a strategy for zero-sum games. The idea was that you set up two fictitious players. The first player makes a random choice of moves, and then the second player does the best thing against what the first player has done. Then the second player takes the average of the two strategies — in other words, weights the probabilities equally — and does the best thing. Then the first player weights the choice of the second player and so on. The question was whether, if this procedure were continued indefinitely, it would converge to a solution of the game. A number of people at Rand had tried to prove that it would. Von Neumann had even looked at the problem. And Rand was offering a \$200 prize for its solution. In my paper, “An iterative method of solving a game” [2], I showed that the procedure did indeed converge; but I didn’t get the prize, because I was a Rand employee. I was once told by David Gale that he considered the theorem in that paper the most important theorem in elementary game theory; but I cannot judge, since I never again did anything in game theory.
Even while employed at Rand, I continued to think about problems of existential definability relevant to Hilbert’s tenth problem. Since there are many classical Diophantine equations with one parameter for which no effective method of determining the solvability for an arbitrary value of the parameter is known, it seemed very unlikely that a decision procedure could be found. But a negative answer would be an answer, too.

In 1950, at the first postwar International Congress at Harvard, Martin Davis, who had just completed his thesis under Emil Post, presented a 10-minute paper on his theorem about reducing recursive enumerable sets to a particular form, and I presented a 10-minute paper on my work on existential definability. That was the first time I had met Martin. I remember that he said he didn’t see how my work could help to solve Hilbert’s problem, since it was just a series of examples. I said, well, I did what I could.
During the 1950s, in another field, I experienced a failure which still embarrasses me. (I think our failures should be included along with our successes.) There was a lot of money available for mathematical research at that time, and Hans Lewy got me into some work on hydrodynamics that was being done at Stanford under Al Bowker. It was not my field, and I shouldn’t have taken it on, but I did. Although I worked very hard, I was able to prove absolutely nothing. When the year was up, I resigned without even turning in a report, I had nothing to report. Bowker later became Chancellor here at Berkeley, and I could hardly bring myself to look him in the face.
After I escaped from hydrodynamics, I read a magazine article about Adlai Stevenson, then the governor of Illinois, which interested me very much. I became even more interested after he was nominated for president and promised in his acceptance speech “to talk sense to the American people.” (This was in the middle of the McCarthy era.) Although I did not entirely abandon mathematics, I spent a lot of time on politics in the next half a dozen years. I was even county manager for Alan Cranston’s first political campaign.
And I continued to struggle with the Tenth Problem. In 1961 Martin Davis, Hilary Putnam, and I published a joint paper, “The undecidability of exponential Diophantine equations” [4], which used ideas from the papers Martin and I had presented at the International Congress along with various new results. The paper contains what is sometimes referred to as the Robinson hypothesis (or, as Martin calls it “J.R.”) to the effect that if there were some Diophantine relation that grew faster than an exponential but not too terribly fast — less than some function that could be expressed in exponentials — then we would be able to define exponentiation. It would follow from the definition that exponential Diophantine equations would be equivalent to Diophantine equations and that, therefore, the solution to Hilbert’s tenth problem would be negative. At the time many people told Martin that this approach was misguided, to say the least. They were more polite to me.
By the time the joint paper was published, my heart had broken down, just as the doctor in San Diego had predicted; and I had to have the open-heart surgery which I mentioned earlier. One month after the operation I bought my first bicycle. It has been followed by half a dozen increasingly better bikes and many cycling trips in this country and in Holland. Raphael sometimes complains that while other men’s wives buy fur coats and diamond bracelets, his wife buys bicycles.
Throughout the 1960s, while publishing a few papers on other things, I kept working on the Tenth Problem; but I was getting rather discouraged. For a while I ceased to believe in the Robinson hypothesis, although Raphael insisted that it was true but just too difficult to prove. I even worked in the opposite direction, trying to show that there was a positive solution to Hilbert’s problem; but I never published any of that work. It was the custom in our family to have a get-together for each family member’s birthday; and when it came time for me to blow out the candles on my cake, I always wished, year after year, that the Tenth Problem would be solved — not that I would solve it, but just that it would be solved. I felt that I couldn’t bear to die without knowing the answer.
Finally — on February 15, 1970 — Martin telephoned me from New York to say that John Cocke had just returned from Moscow with the report that a 22-year-old mathematician in Leningrad had proved that the relation \( n=F_{2m} \), where \( F_{2m} \) is a Fibonacci number, is Diophantine. This was all that we needed. It followed that the solution to Hilbert’s tenth problem is negative — a general method for determining whether a given Diophantine equation has a solution in integers does not exist.
Martin did not know the name of the mathematician or the method he had used. I was so excited by the news that I wanted to call Leningrad right away to find out if it were really true. Raphael and other people here said no, hold on — the world had gone for seventy years without knowing the solution to the tenth problem, surely I could wait a few more weeks! I wasn’t so sure. Fortunately I didn’t have to wait that long. Three days later John McCarthy called from Stanford to say that in Novosibirsk he had heard a talk by Ceitin on the proof, which was the work of a mathematician named Yuri Matijasevic. John had taken notes on Ceitin’s talk. While he was doing so, he had felt that he understood the proof; but by the time he got back to Stanford he found that he couldn’t make much sense of his notes. He offered to send them to me if I wanted to see them. Of course I wanted to, very much.
When I received the notes, I sent a copy to Martin even before I went over them myself. He told me later that he was always glad that I had let him go through them on his own. It was the next best thing to solving the problem.
It was quite immediately clear what Matijasevic had done. By using the Fibonacci numbers, a series which had been known to mathematicians since the beginning of the thirteenth century, he had been able to construct a function that met the requirements of the Robinson hypothesis. There was nothing in his proof which would not be included in a course in elementary number theory!
Just one week after I had first heard the news from Martin, I was able to write to Matijasevic:
“…[N]ow I know it is true, it is beautiful, it is wonderful.”
“If you are really 22 [he was], I am especially pleased to think that when I first made the conjecture you were a baby and I just had to wait for you to grow up!”
That year when I went to blow out the candles on my cake, I stopped in mid-breath, suddenly realizing that the wish I had made for so many years had actually come true.
I have been told that some people think that I was blind not to see the solution myself when I was so close to it. On the other hand, no one else saw it either. There are lots of things, just lying on the beach as it were, that we don’t see until someone else picks one of them up. Then we all see that one.
In 1971 Raphael and I visited Leningrad and became acquainted with Matijasevic and his wife, Nina, a physicist. At that time, in connection with the solution of Hilbert’s problem and the role played in it by the Robinson hypothesis, Linnik told me that I was the second most famous Robinson in the Soviet Union, the first being Robinson Crusoe. Yuri and I have since written two papers together; and, after the 1974 De Kalb symposium on the Hilbert problems, Martin, Yuri, and I collaborated on a paper entitled “Positive aspects of a negative solution” [5].

I have written so incompletely and nontechnically about my more than twenty years of work on the Tenth Problem because Martin, who contributed as much as I to its ultimate solution, has published several excellent papers telling the whole story. These include both a popular account in Scientific American and a technical one in The American Mathematical Monthly.
When any one of Hilbert’s problems is solved or even some progress made toward a solution, everybody who has had any part in the work gets a great deal of attention. In 1975, for instance, I became the first woman mathematician to be elected to the National Academy of Sciences, although there are other women mathematicians who in my opinion are more deserving of the honor.
When the University press office received the news, someone there called the mathematics department to find out just who Julia Robinson was. “Why, that’s Professor Robinson’s wife.” “Well,” replied the caller, “Professor Robinson’s wife has just been elected to the National Academy of Sciences.” Up to that time I had not been an official member of the University’s mathematics faculty, although from time to time I had taught a class at the request of the department chairman. In fairness to the University, I should explain that because of my health, even after the heart operation, I would not have been able to carry a full-time teaching load. As soon as I was elected to the Academy, however, the University offered me a full professorship with the duty of teaching one-fourth time — which I accepted.
In 1982 I was nominated for the presidency of the American Mathematical Society. I realized that I had been chosen because I was a woman and because I had the seal of approval, as it were, of the National Academy. After discussion with Raphael, who thought I should decline and save my energy for mathematics, and other members of my family, who differed with him, I decided that as a woman and a mathematician I had no alternative but to except. I have always tried to do everything I could to encourage talented women to become research mathematicians. I found my service as president of the Society taxing but very, very satisfying.
Other honors, including election to the American Academy of Arts and Sciences, an honorary degree from Smith College, and a generous grant from the MacArthur Foundation, have come with disconcerting speed. Even more general notice has been taken of me. Vogue and The Village Voice have inquired after my opinions, and The Ladies’ Home Journal has included me in a list of the 100 most outstanding women in America.
All this attention has been gratifying but also embarrassing. What I really am is a mathematician. Rather than being remembered as the first woman this or that, I would prefer to be remembered, as a mathematician should, simply for the theorems I have proved and the problems I have solved.