by Rob Kirby
The Whitney trick is a method for removing points of intersection between two submanifolds. It can be seen in its most elementary form in Figure 1, in which it is obvious that the two points of intersection can be removed by an isotopy (a 1-parameter family of embeddings) of the arc labeled \( P^p \) which pulls the arc across the disk \( D \). (Note that \( x \) and \( y \) have opposite signs.) More generally the Whitney trick is used to remove a pair of intersections, \( x \) and \( y \), between two manifolds \( P^p \) and \( Q^q \) which are embedded in an ambient manifold \( M^{p+q} \). To see how this is done, we first construct a model, then show how to embed it in \( M \) (if possible), and then sketch some applications of the Whitney trick.
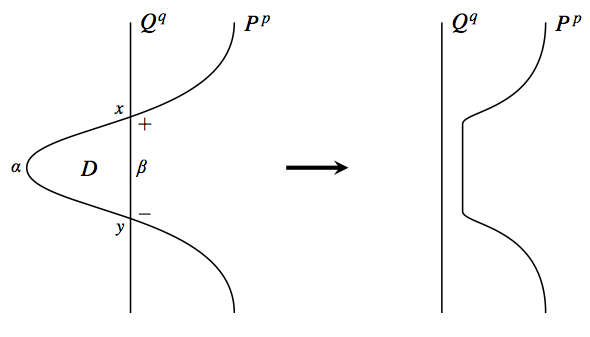
The model is merely a stabilization of the example in Figure 1. We cross the plane in which \( D \) is embedded with \( \mathbb R^{(p-1) + (q-1)} \) so that the ambient space is just \( \mathbb R^{p+q} \), and then we cross the curve which includes \( \alpha \) by \( \mathbb R^{p-1} \) to get an \( p \)-dimensional manifold \( P \), and similarly cross with \( \mathbb R^{q-1} \) to get an \( q \)-manifold \( Q \). These two manifolds still meet in two points \( x \) and \( y \), which are connected in \( P \) by the original arc \( \alpha \) and in \( Q \) by the original arc \( \beta \). Note that the two arcs still bound a 2-dimensional disk \( D \), and that \( D \) lies inside a larger open disk \( \Delta \) in the plane. Also note that \( \Delta \) has a normal \( (p-1)+(q-1) \)-plane bundle which splits as the direct sum (also called “Whitney sum”) of a \( (p-1) \)-plane bundle which coincides along \( \alpha \) with the normal bundle of \( \alpha \) in \( P \), and an \( (q-1) \)-plane bundle which coincides along \( \beta \) with the normal bundle of \( \beta \) in \( Q \).
The plane isotopy described in Figure 1 easily extends to an isotopy taking place in the plane crossed with the \( p-1 \) coordinates of \( P \), as drawn for \( p=2 \) in Figure 2 [e4]; nothing happens with the other \( q-1 \) coordinates.
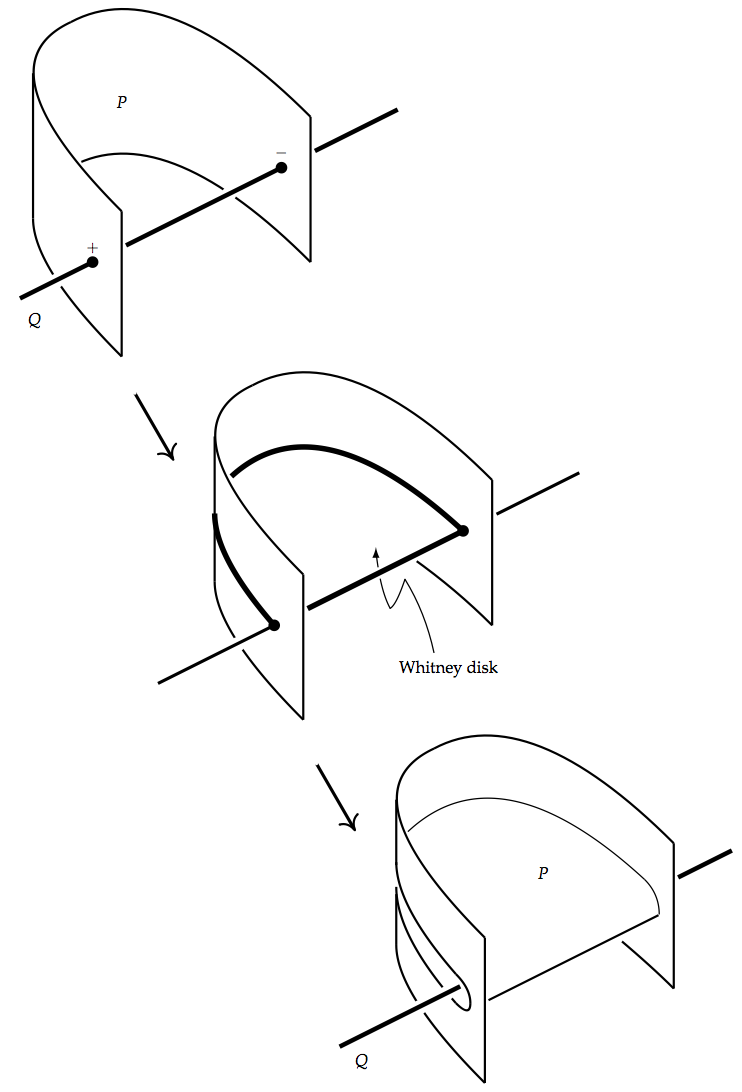
Now this model must be embedded in \( M^{p+q} \) so that the actual manifolds \( P \) and \( Q \) and two points of intersection \( x \) and \( y \) correspond to the manifolds and points in the model.
If both \( P \) and \( Q \) are connected, then the arcs \( \alpha \) and \( \beta \) exist, and if \( P \) and \( Q \) are simply connected (as they often are in applications), then the arcs are unique up to homotopy. If \( M \) is simply connected, then the disk \( D \) can be mapped into \( M \). If not, then \( x \) must be connected by an arc (unique up to homotopy if \( P \) is simply connected) to a base point \( x_0 \in P \) which is connected by an arc to a base point \( z \in M \). Similarly with arcs to a base point \( y_0 \in Q \). It follows that \( x \) then determines an element of \( \pi_1(M) \) by running from \( z \) to \( x_0 \) to \( x \) to \( y_0 \) and back to \( z \). Now if \( x \) and \( y \) both represent the same element of \( \pi_1(M) \), then we can still map a disk \( D \) into \( M \). (This is important in proving the \( s \)-cobordism theorem.)
Once \( D \) is mapped into \( M \), we can embed it if the dimension of \( M \), \( p+q \), is five or more. Furthermore, if each of \( p \) and \( q \) is three or more, then the embedding of \( D \) can be chosen to miss \( P \) and \( Q \) except along its boundary.
Now that \( D \) is embedded missing \( P \) and \( Q \), it remains to find the embedding of the normal bundle of \( D \). The normal \( (p+q-2) \)-bundle to \( D \) (in fact, \( \Delta \)) in \( M \) can be split along \( \alpha \) as the normal \( (p-1) \)-bundle to \( \alpha \) in \( P \) direct sum the orthogonal \( (q-1) \)-bundle. That splitting extends across \( \Delta \). The only problem remaining is that this \( (p-1) \)-plane bundle may not coincide with the \( (p-1) \)-plane bundle which is the normal bundle to \( \beta \) in \( Q \).
The problem reduces to an arc of \( (p-1) \)-planes in \( \mathbb R^{(p-1) + (q-1)} \) which we want to isotope to the trivial arc, relative to the endpoints. Note that the trivial arc, as in the model, corresponds to \( x \) and \( y \) having opposite signs, so this is necessary. Now, this is possible because the fundamental group of the Stiefel manifold of \( (p-1) \)-planes in \( \mathbb R^{p+q-2} \) is trivial when \( p > 2 \) (see [e3], p. 202). For more details, see the excellent description in [e4].
Whitney developed the Whitney trick in order to embed \( P^p \) in \( \mathbb R^{2p} \) [e1]. For \( p=2 \), this is easy. In higher dimensions, \( P \) only immerses in \( \mathbb R^{2p} \) (by general position), so for each double point, Whitney introduces in local fashion another double point of opposite sign (some thought is needed if \( P \) is non-orientable), and then uses the Whitney trick to remove both points of intersection.
A later, and crucial, use of the Whitney trick is in Smale’s proof of the \( h \)-cobordism theorem [e2].