Celebratio Mathematica

Rob Kirby was my Ph.D. su­per­visor at UC Berke­ley; I fin­ished my Ph.D. there in 1999. Dur­ing my first postdoc po­s­i­tion, at the Uni­versity of Ari­zona, my postdoc ad­visor Doug Pick­rell sug­ges­ted that I in­vite Rob to give a col­loqui­um talk; I think that was in the fall of 2001. I re­mem­ber Rob gave a sur­vey of the be­gin­ning of Hee­gaard Flo­er the­ory and in par­tic­u­lar I clearly re­mem­ber him say­ing something about or­gan­iz­ing the vari­ous spin\( ^\mathbb{C} \) struc­tures on a 4-man­i­fold in­to “buck­ets”. However, the key event of that vis­it for me was a full-moon night hike that Doug or­gan­ized at Sabino Canyon. (Part of my point here in the story is to make sure to give Doug due cred­it for his role in all of this. An­oth­er point is to em­phas­ize the im­port­ance of hik­ing in Rob’s math­em­at­ic­al life.) Dur­ing the hike, we ended up talk­ing about my thes­is work on handle-by-handle sym­plect­ic con­struc­tions, and I re­mem­ber Rob com­ment­ing, “Oh, so that’s what your thes­is was about.” The point is not that he didn’t read my thes­is but that the es­sen­tial idea of my thes­is was some­how ob­scured in the whole mech­an­ics of writ­ing, re­view­ing, gradu­at­ing, and so forth; I do know that Rob and I both talked about most of the de­tails of my thes­is but some­how we had nev­er stepped back and thought about what it was really about. And once Rob un­der­stood what it was really about, the ideas star­ted flow­ing.

In this art­icle I want to tell the (mostly math­em­at­ic­al) story of my col­lab­or­a­tion with Rob Kirby that star­ted dur­ing that night hike and ended up with our dis­cov­ery of tri­sec­tions of 4-man­i­folds [5]. I use “dis­cov­ery” cau­tiously be­cause much of what we dis­covered was already known and in the end a lot of our work can be thought of as just find­ing the right way to or­gan­ize the ideas and the ques­tions. Our work star­ted hov­er­ing around vari­ous to­po­lo­gic­al con­struc­tions re­lated to the vis­ion of ex­tend­ing 4-di­men­sion­al sym­plect­ic tools to a lar­ger class of 4-man­i­folds us­ing near-sym­plect­ic struc­tures (in­spired by Cliff Taubes). We then fol­lowed what seemed like the nat­ur­al math­em­at­ic­al trail to the study of broken Lef­schetz fibra­tions (in­spired by Auroux, Don­ald­son and Katzarkov, Ush­er and Per­utz), then to think­ing more gen­er­ally about gen­er­ic maps from 4-man­i­folds to sur­faces (in­spired by Lekili), which we ended up call­ing Morse 2-func­tions. (A lot of this in­volved re­dis­cov­er­ing for ourselves in our own way of un­der­stand­ing lots of things already known to sin­gu­lar­ity the­or­ists and oth­ers.) From there we more or less stumbled on tri­sec­tions of 4-man­i­folds as a par­tic­u­larly nice out­come of the the­ory of Morse 2-func­tions. At the end I will give a brief sur­vey of some of the de­vel­op­ments sur­round­ing tri­sec­tions that have happened since our first pa­per, em­phas­iz­ing my work with Rob and Aaron Ab­rams [6] on group tri­sec­tions.

I hope to em­phas­ize throughout the power­ful in­flu­ence of Rob’s unique way of see­ing the math­em­at­ic­al world on my own math­em­at­ic­al de­vel­op­ment and the nat­ur­al­ness of the math­em­at­ic­al flow of our col­lab­or­a­tion. When I was a gradu­ate stu­dent and asked Rob for some ad­vice about what to think about math­em­at­ic­ally, I don’t re­mem­ber the ex­act con­text, but I re­mem­ber clearly that his ad­vice was sim­ul­tan­eously vague, un­help­ful and deeply mean­ing­ful: “Fol­low your nose.”

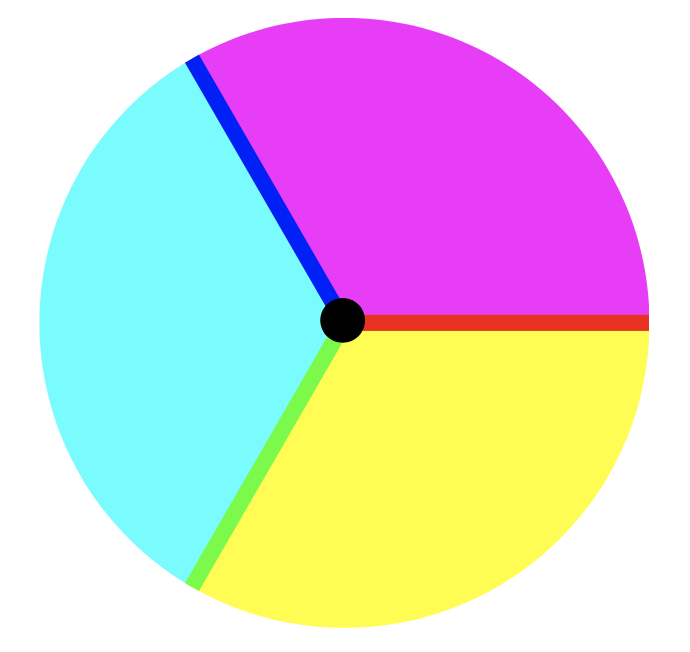
For those who have not thought about tri­sec­tions be­fore, the idea is al­most stu­pidly simple. A tri­sec­tion of a smooth, closed, ori­ented, con­nec­ted 4-man­i­fold \( X \) is a de­com­pos­i­tion of \( X \) in­to three to­po­lo­gic­ally simple pieces \[ X = X_1 \cup X_2 \cup X_3 \] which fit to­geth­er like three “slices of a pie” as in Fig­ure 1: Each piece \( X_i \) is dif­feo­morph­ic (after some mild smooth­ing of corners) to a reg­u­lar neigh­bor­hood of a bou­quet of (zero or more) circles in \( \mathbb{R}^4 \). (A bou­quet of zero circles is a point, one circle is a circle, two circles is a fig­ure eight, etc.) Each pair­wise in­ter­sec­tion \( X_i \cap X_j \) is dif­feo­morph­ic to a reg­u­lar neigh­bor­hood of a bou­quet of (zero or more) circles in \( \mathbb{R}^3 \) (a.k.a. a sol­id handle­body). The triple in­ter­sec­tion \( X_1 \cap X_2 \cap X_3 \) is dif­feo­morph­ic to a closed, ori­ent­able, con­nec­ted sur­face.

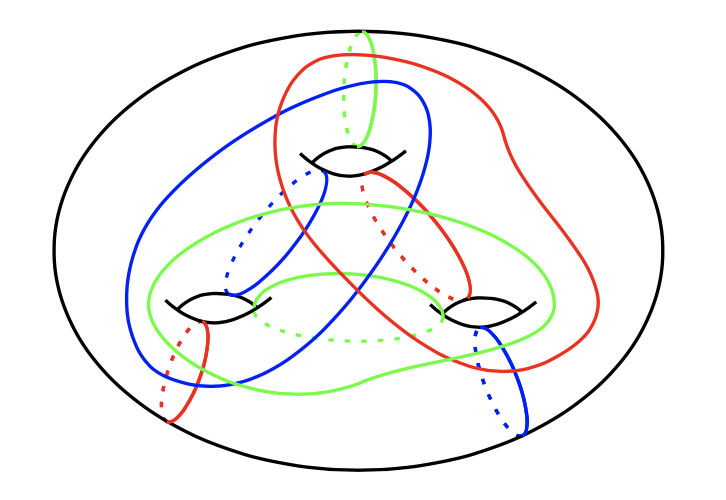
The sur­pris­ing facts which we dis­covered between 2011 and 2013 are (i) that every smooth, closed, ori­ented, con­nec­ted 4-man­i­fold has a tri­sec­tion (ex­ist­ence), and in fact it has lots of them; (ii) that there is a simple-to-de­scribe sta­bil­iz­a­tion op­er­a­tion that in­creases the com­plex­ity of a tri­sec­tion; and (iii) that any two tri­sec­tions of a giv­en 4-man­i­fold have a com­mon sta­bil­iz­a­tion (unique­ness). Fur­ther­more, this means that every such 4-man­i­fold can be de­scribed up to dif­feo­morph­ism by a tri­sec­tion dia­gram which is a dia­gram drawn on a closed, ori­ented sur­face of genus \( g \) in­volving \( g \) red simple closed curves, \( g \) blue simple closed curves, and \( g \) green simple closed curves. See Fig­ure 2 for an in­ter­est­ing ex­ample. The sur­face is the triple in­ter­sec­tion and the curves of each col­or are curves that bound disks in the pair­wise in­ter­sec­tions.

One form­ally sat­is­fy­ing fea­ture of tri­sec­tions is that they turn out to be the right gen­er­al­iz­a­tion of the no­tion of a Hee­gaard split­ting of a 3-man­i­fold to the world of 4-man­i­folds, with the sur­prise be­ing that in or­der to gen­er­al­ize a Hee­gaard split­ting (a de­com­pos­i­tion of a 3-man­i­fold in­to two simple pieces) one needs to con­sider de­com­pos­i­tions in­to three pieces. In fact Hee­gaard split­tings of a 3-man­i­fold \( M \) are best seen as com­ing from par­tic­u­larly nice smooth maps \( f: M \to [-1,1] \) (Morse func­tions with well or­gan­ized crit­ic­al points) and then de­com­pos­ing \( M \) in­to \( f^{-1}([-1,0]) \) and \( f^{-1}([0,1]) \). Sim­il­arly, tri­sec­tions of a 4-man­i­fold \( X \) are best seen as com­ing from par­tic­u­larly nice smooth maps \( f: X \to D^2 \) to the disk, called Morse 2-func­tions, with par­tic­u­larly well or­gan­ized sin­gu­lar­it­ies, and then de­com­pos­ing in­to three pieces by pulling back the de­com­pos­i­tion of the disk in­to three (fat) pie slices. Also, Hee­gaard split­tings al­low 3-man­i­folds to be de­scribed by Hee­gaard dia­grams, which are just like tri­sec­tion dia­grams but only in­volve curves of two col­ors. Fi­nally, note that a tri­sec­tion dia­gram gives three Hee­gaard dia­grams, by con­sid­er­ing each pair of two col­ors.

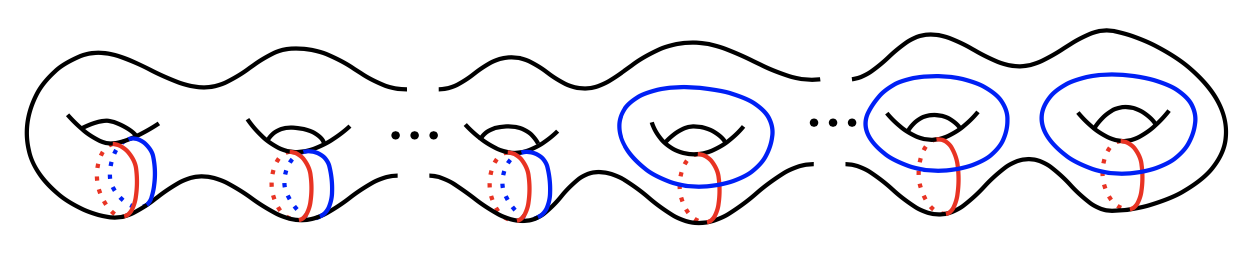
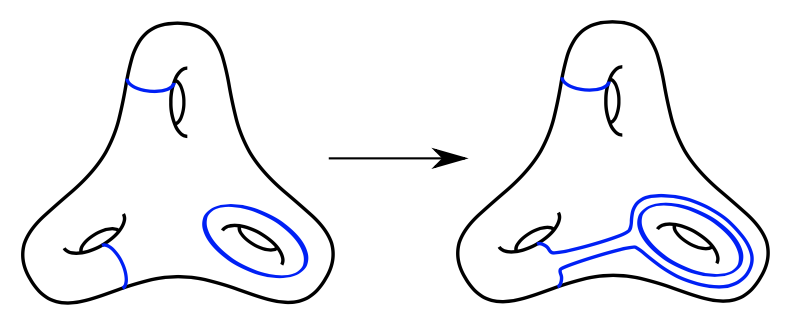
In prin­ciple, a tri­sec­tion dia­gram is not much dif­fer­ent from a framed link dia­gram, but it is bet­ter or­gan­ized, and there are al­gorithms to turn either one in­to the oth­er. In par­tic­u­lar, tri­sec­tion dia­grams have an in­ter­est­ing form­al prop­erty sum­mar­ized in the slo­gan “pair­wise bor­ing, triply in­ter­est­ing”. There is a stand­ard move on a col­lec­tion of dis­joint simple closed curves on a sur­face, called a handle slide, which in­volves one curve “slid­ing over” and pick­ing up a copy of an­oth­er curve, as shown in Fig­ure 3. Handle slides do not change either the 4-man­i­fold as­so­ci­ated to a tri­sec­tion dia­gram or the 3-man­i­fold as­so­ci­ated to a Hee­gaard dia­gram. A tri­sec­tion dia­gram \( (\Sigma, \alpha.\beta,\gamma) \) has the prop­erty that each as­so­ci­ated Hee­gaard dia­gram of two col­ors \( (\Sigma,\alpha,\beta) \), \( (\Sigma,\beta,\gamma) \) and \( (\Sigma,\gamma,\alpha) \) is equi­val­ent, after some handle slides and a dif­feo­morph­ism, to the bor­ing Hee­gaard dia­gram in Fig­ure 4, which is a Hee­gaard dia­gram for the con­nec­ted sum of some num­ber of \( S^1 \times S^2 \)s (a bor­ing 3-man­i­fold). However, all 4-man­i­folds (and thus a very large class of very in­ter­est­ing ob­jects) can be de­scribed by these triples of col­lec­tions of curves, des­pite the fact that in pairs they are bor­ing. The in­ter­ested read­er might en­joy veri­fy­ing this pair­wise stand­ard­ness for the dia­gram in Fig­ure 2.

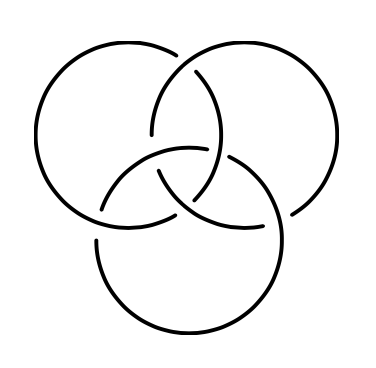
A clas­sic­al ex­ample of the “pair­wise bor­ing, triply in­ter­est­ing” slo­gan, by the way, is the three-com­pon­ent link known as the Bor­romean rings, shown in Fig­ure 5. This link of three circles has the prop­erty than any pair of the three are un­linked but all to­geth­er they are non­trivi­ally linked. Here is a meta-ques­tion for the math­em­at­ic­al com­munity at large: Where else in math­em­at­ics does this slo­gan ap­ply?

My en­tire to­po­lo­gic­al ca­reer has been dom­in­ated by the in­cred­ible twin res­ults of Freed­man [e5] that two closed simply con­nec­ted smooth 4-man­i­folds are homeo­morph­ic if and only if they are ho­mo­topy equi­val­ent and of Don­ald­son [e6] that there ex­ist in­vari­ants that can dis­tin­guish pairs (known as “exot­ic pairs”) of closed, simply con­nec­ted smooth 4-man­i­folds that are ho­mo­topy equi­val­ent but not dif­feo­morph­ic. Rob was closely con­nec­ted with Freed­man’s work, but Don­ald­son’s work used gauge the­ory (PDEs com­ing from phys­ics), and Rob was nev­er a gauge the­or­ist. Ever since I have known Rob an im­port­ant part of his math­em­at­ic­al quest has been to un­der­stand in some “genu­inely to­po­lo­gic­al” how to see that exot­ic pairs are not dif­feo­morph­ic. The Don­ald­son in­vari­ants were later re­placed to some ex­tent with the sim­pler Seiberg–Wit­ten in­vari­ants [e9] and even­tu­ally many gauge the­or­et­ic res­ults could be proved us­ing Oz­sváth and Szabó’s Hee­gaard Flo­er in­vari­ants [e19], but, still, un­der­ly­ing it all is the prob­lem of count­ing solu­tions to PDEs. Rob al­ways wanted a way to see what we were count­ing ex­pli­citly and com­bin­at­or­i­ally, and to see from a geo­met­ric to­po­lo­gist’s per­spect­ive, in a dir­ect way, why these counts were in­vari­ants of smooth struc­tures.

We would like to be able to stare at some dia­gram­mat­ic, com­bin­at­or­i­al de­scrip­tion of a 4-man­i­fold, “count” something in the dia­gram, per­haps count smooth iso­topy classes of some ob­jects in the dia­gram, and then un­der­stand that this is an in­vari­ant be­cause one un­der­stands the moves needed to re­late any two such dia­gram­mat­ic de­scrip­tions of the same 4-man­i­fold. I would ar­gue that we are still far from such a per­spect­ive, but that for form­al reas­ons such a per­spect­ive should be out there. The closest we have come that I am aware of are the hand­ful of 4-di­men­sion­al res­ults com­ing out of Khovan­ov ho­mo­logy, be­gin­ning with Rasmussen’s com­pu­ta­tions of slice genus [e22].1 In what fol­lows, one thread of the story of my col­lab­or­a­tion with Rob is that we were con­stantly try­ing to catch up with gauge and Flo­er the­ory and re­in­ter­pret it in ways we non­ana­lyt­ic­ally minded “mere geo­met­ric to­po­lo­gists” could un­der­stand and really see.

Gen­er­ally, however, al­most all in­vari­ants pro­ceed by first im­pos­ing some ad­di­tion­al struc­ture, then count­ing something, and then show­ing that the an­swer does not de­pend on the choice of that ad­di­tion­al struc­ture. In the gauge the­or­et­ic con­text this ad­di­tion­al struc­ture is a col­lec­tion of dif­fer­en­tial geo­met­ric data such as Rieman­ni­an met­rics, con­nec­tions on vari­ous bundles, and so forth. In the Flo­er the­or­et­ic set­ting the ad­di­tion­al struc­ture is gen­er­ally an al­most com­plex struc­ture, usu­ally with a sym­plect­ic struc­ture lurk­ing in the back­ground. In our hy­po­thet­ic­ally more “com­bin­at­or­i­al”, more “to­po­lo­gic­ally un­der­stand­able” vis­ions, there would still be ex­tra struc­ture, but this would come in the form of a dia­gram de­scrib­ing a con­struc­tion of the man­i­fold or simply a de­com­pos­i­tion of the man­i­fold in­to ele­ment­ary pieces. For us, in­spired heav­ily by Morse the­ory, an in­ter­me­di­ate struc­ture has typ­ic­ally been some kind of smooth map from the man­i­fold in ques­tion to an­oth­er sim­pler man­i­fold, e.g., \( \mathbb{R} \) or \( \mathbb{R}^2 \) or \( S^2 \). Sym­plect­ic to­po­logy has al­ways lurked in the back­ground as “bor­der­line un­der­stand­able” to simple minded to­po­lo­gists, and thus you will find the fol­low­ing storyline pro­gresses through sym­plect­ic to­po­logy to un­der­stand­ing vari­ous classes of maps from di­men­sion 4 to di­men­sion 2 and fi­nally ar­riv­ing at de­com­pos­i­tions of man­i­folds and as­so­ci­ated dia­grams, with an ad­dendum in which the “dia­grams” are even­tu­ally re­placed with group the­ory.

There is a great deal also to be said about the ex­tent to which com­plex al­geb­ra­ic geo­metry has in­spired smooth 4-di­men­sion­al to­po­logy, with smooth al­geb­ra­ic sur­faces be­ing in some sense the pro­to­typ­ic­al 4-man­i­folds. This is too much for me to com­pet­ently dis­cuss here but suf­fice it to say that this thread very much lurks in the back­ground, and I be­lieve that much of Rob’s in­sight in­to the prob­lems he and I have thought about can be traced back to his early work with Harer and Kas on the smooth to­po­logy of com­plex sur­faces [1]. (To a com­plex al­geb­ra­ic geo­met­er, a quick in­tro­duc­tion to tri­sec­tions is to say that they are the nat­ur­al gen­er­al­iz­a­tion of the de­com­pos­i­tion of the com­plex pro­ject­ive plane in­to three co­ordin­ate charts.)

Per­haps a bet­ter reas­on for this quest than just the fact that we couldn’t un­der­stand gauge the­ory is that all gauge the­or­et­ic meth­ods have failed to say any­thing about ho­mo­topy 4-spheres, and thus shed no light on the holy grail, the smooth 4-di­men­sion­al Poin­caré con­jec­ture (or its sis­ter, the smooth 4-di­men­sion­al Schoen­flies prob­lem). Thus, like any good 4-di­men­sion­al to­po­lo­gist should, we have al­ways held out hope that some day we might stumble upon some in­vari­ant, al­most cer­tainly not defined us­ing any­thing like gauge the­ory, which could dis­tin­guish smooth ho­mo­topy 4-spheres and hence dis­prove the Poin­caré con­jec­ture. Own­ing up to such a dream in pub­lic is per­haps not good form, but in our col­lab­or­a­tion we have had mo­ments of (prob­ably mis­guided) op­tim­ism and en­thu­si­asm in this dir­ec­tion. The truth is that we have been fre­quently quite na­ive about the po­ten­tial to make hard things easy to un­der­stand, but that our naïveté seems to have served us pretty well.

In what fol­lows I will try to give a fairly thor­ough ac­count of the path Rob and I took that brought us to think­ing about tri­sec­tions of 4-man­i­folds. Of course we nev­er knew where we were go­ing in the long run, but we looked at a se­quence of re­lated prob­lems that each raised new ques­tions that, in hind­sight, seemed to lead in­ex­or­ably to­wards tri­sec­tions. All of the ques­tions we thought about along the way are, in my opin­ion, still very im­port­ant and serve to set tri­sec­tions in the right con­text. At each step we were work­ing on 4-man­i­folds equipped with cer­tain aux­il­i­ary struc­tures, and I will de­scribe those aux­il­i­ary struc­tures as they arise.

The rel­ev­ant aux­il­i­ary struc­tures to dis­cuss here are sym­plect­ic and al­most com­plex struc­tures on 4-man­i­folds, build­ing on the found­a­tion­al work of Gro­mov [e7]. Sym­plect­ic struc­tures are closed, nonde­gen­er­ate 2-forms, which means one can al­ways find loc­al co­ordin­ates in which they have (in di­men­sion 4) the form \( dx_1 \wedge dy_1 + dx_2 \wedge dy_2 \). (A 2-form at a point is an an­ti­sym­met­ric bi­lin­ear form on the tan­gent space at that point that should be thought of meas­ur­ing the “signed area” of the par­al­lel­o­gram spanned by two vec­tors, and in this case the area of the \( 1 \times 1 \) squares in the \( x_1,y_1 \) and \( x_2,y_2 \) planes are 1 while the \( 1 \times 1 \) squares in any of the \( x_1,x_2 \), \( x_1,y_2 \), \( y_1,x_2 \) and \( y_1,y_2 \) planes have “area” 0.) An al­most com­plex struc­ture on a 4-man­i­fold is a way to “mul­tiply by \( i \)” in the tan­gent spaces, in oth­er words a smoothly vary­ing lin­ear auto­morph­ism \( J \) of each tan­gent space such that \( J^2 = -\operatorname{id} \). The struc­ture of a 2-di­men­sion­al com­plex man­i­fold on a 4-man­i­fold in­duces an al­most com­plex struc­ture on the tan­gent spaces, but not every al­most com­plex struc­ture comes from a com­plex man­i­fold struc­ture.

A clas­sic­al way to probe the struc­ture of a com­plex al­geb­ra­ic vari­ety is to study enu­mer­at­ive prob­lems for curves in that vari­ety. Re­mem­ber­ing that “curves” over \( \mathbb{C} \) are ac­tu­ally real 2-di­men­sion­al sur­faces, one can push these enu­mer­at­ive meth­ods to the softer set­ting of al­most com­plex man­i­folds and study pseudo­holo­morph­ic curves, which are sur­faces in the 4-man­i­fold whose tan­gent spaces are fixed by the al­most com­plex struc­ture, in oth­er words, their real 2-di­men­sion­al tan­gent spaces are ac­tu­ally com­plex lines with re­spect to \( J \). Gro­mov’s key con­tri­bu­tion was to show that, when an al­most com­plex struc­ture is dom­in­ated by a sym­plect­ic struc­ture (mean­ing that the 2-form as­signs pos­it­ive area to a par­al­lel­o­gram spanned by \( V \) and \( JV \) for any nonzero tan­gent vec­tor \( V \)), then one can con­trol fam­il­ies of pseudo­holo­morph­ic curves and get com­pact­ness res­ults for their mod­uli spaces. This then al­lows, in spe­cial cases, for one to have well-defined counts of pseudo­holo­morph­ic curves and prove that these counts are in­vari­ant un­der vari­ous choices. Note that the pseudo­holo­morph­ic con­di­tion on an em­bed­ding of a sur­face is ba­sic­ally a par­tial dif­fer­en­tial equa­tion, so look­ing for pseudo­holo­morph­ic curves is ba­sic­ally count­ing solu­tions to a PDE, but some­how it feels a little more con­crete than the PDEs in­volved in gauge the­ory.

Re­turn­ing now to the pro­ject of find­ing a more “con­crete” or “geo­met­ric to­po­lo­gist friendly” un­der­stand­ing of gauge the­or­et­ic in­vari­ants of smooth 4-man­i­folds, Taubes [e11] showed that, when a 4-man­i­fold sup­ports a sym­plect­ic struc­ture, its Seiberg–Wit­ten (SW) in­vari­ants can be cal­cu­lated by count­ing pseudo­holo­morph­ic curves with re­spect to a gen­er­ic al­most com­plex struc­ture dom­in­ated by that sym­plect­ic struc­ture, in oth­er words, a Gro­mov in­vari­ant (Gr). This res­ult is gen­er­ally sum­mar­ized as SW=Gr. This has a range of spec­tac­u­lar im­plic­a­tions, but when handed a ran­dom 4-man­i­fold, it might not be so clear wheth­er it has a sym­plect­ic struc­ture or not. On the oth­er hand, Taubes, Honda [e16] and oth­ers had ob­served that every 4-man­i­fold with \( b_2^+ > 0 \), which means that it con­tains sur­faces which have pos­it­ive signed in­ter­sec­tion num­ber with any wiggled ver­sions of them­selves, sup­ports a “near sym­plect­ic” struc­ture. This is a closed 2-form which is sym­plect­ic away from a 1-di­men­sion­al locus where it is zero, and along this locus it van­ishes trans­versely in the ap­pro­pri­ate sense, so that its zero locus is a 1-man­i­fold in a neigh­bor­hood of which the 2-form has a stand­ard mod­el. Taubes floated the idea that per­haps suit­ably defined Gro­mov in­vari­ants in this set­ting would re­cov­er Seiberg–Wit­ten in­vari­ants for ar­bit­rary 4-man­i­folds with \( b_2^+ \) pos­it­ive, and ini­ti­ated a study [e13] of the be­ha­vi­or of pseudo­holo­morph­ic curves in the stand­ard loc­al mod­el near the van­ish­ing locus. This line of reas­on­ing seems to have fi­nally reached fruition with Chris Gerig’s work [e26], which is also a bet­ter re­source than this para­graph for a prop­er ac­count of the his­tory and the mo­tiv­a­tion for the idea.

Still, the fact that every 4-man­i­fold with pos­it­ive \( b_2^+ \) sup­ports a near sym­plect­ic struc­ture was not con­struct­ive, however, so if the SW=Gr plan panned out in the near sym­plect­ic set­ting it was still not clear how use­ful that would be if one did not know how to ex­pli­citly con­struct a near sym­plect­ic form on a par­tic­u­lar 4-man­i­fold. After our Sabino Canyon hike, Rob ex­plained these ideas to me and then Rob and I set out to solve this prob­lem [2], where “ex­pli­citly” meant to us “start­ing from a framed link dia­gram de­scrib­ing a handle de­com­pos­i­tion of the 4-man­i­fold” and then pro­ceed­ing in something that might loosely be called an al­gorithm.

It is im­port­ant to point out here that in the end it is a bit disin­genu­ous to de­scribe our con­struc­tion as ex­pli­cit be­cause of one key point; at a crit­ic­al stage in our con­struc­tion we had two near-sym­plect­ic sym­plect­ic struc­tures, one on one half of the 4-man­i­fold and one on the oth­er, and we needed to glue them to­geth­er along the sep­ar­at­ing 3-man­i­fold. There is a stand­ard way to do this, us­ing a con­tact struc­ture on the 3-man­i­fold as the ap­pro­pri­ate glu­ing bound­ary data. (If you don’t know what a con­tact struc­ture is, just know that it is the cor­rect bound­ary data for sym­plect­ic struc­tures.) In or­der to glue, we needed to know that the con­tact struc­tures com­ing from the con­struc­tions on the two halves were equal (or could be de­formed to be equal). We knew this thanks to Eli­ash­berg’s res­ult [e8] that a cer­tain class of con­tact struc­tures, known as over­twisted con­tact struc­tures, could be clas­si­fied us­ing al­geb­ra­ic to­po­lo­gic­al in­vari­ants, so we ad­jus­ted our con­struc­tion ap­pro­pri­ately to make sure that the in­vari­ants com­ing from the two sides matched. However it is not at all clear that Eli­ash­berg’s ma­chinery to go from know­ing that the in­vari­ants match to de­form­ing (iso­top­ing) the con­tact struc­tures to be equal is “ex­pli­cit”.

The aux­il­i­ary struc­tures of con­cern here are Lef­schetz fibra­tions; for a good over­view see Gom­pf’s ex­pos­i­tion in the No­tices of the AMS [e18]. In short, a Lef­schetz fibra­tion on an ori­ented 4-man­i­fold \( X \) is a smooth map from \( X \) to the 2-sphere \( S^2 \) which has fi­nitely many isol­ated sin­gu­lar­it­ies, each of which is loc­ally modeled (re­spect­ing ori­ent­a­tions) on the simplest sin­gu­lar­ity that can arise in a holo­morph­ic map from \( \mathbb{C}^2 \) to \( \mathbb{C} \): \( (z_1,z_2) \mapsto z_1^2+z_2^2 \). Away from these sin­gu­lar­it­ies, the map thus looks like a sur­face bundle over a sur­face, so loc­ally like \( \Sigma \times B^2 \to B^2 \) for some sur­face \( \Sigma \). To get a more to­po­lo­gic­al un­der­stand­ing of what it means to sup­port a sym­plect­ic struc­ture, Don­ald­son [e10] showed that, after blow­ing up enough times, all sym­plect­ic 4-man­i­folds sup­port Lef­schetz fibra­tions. (“Blow­ing up”, des­pite its name, is a mild op­er­a­tion that changes a man­i­fold in a very con­trolled way so as to al­low two sur­faces that in­ter­sect to be­come dis­joint, at the ex­pense of in­tro­du­cing a new sur­face, called the ex­cep­tion­al di­visor, that they both in­ter­sect; as long as one keeps track of the ex­cep­tion­al di­visor one still has ac­cess to the ori­gin­al man­i­fold and all of its to­po­logy.) With this in mind, Ush­er [e15] showed that one could re­cov­er the full Gro­mov pseudo­holo­morph­ic curve count by a cer­tain count of pseudo­holo­morph­ic “multi­sec­tions” of sym­plect­ic Lef­schetz fibra­tions, ar­gu­ably mak­ing Taubes’ \( \text{SW}=\text{Gr} \) res­ult slightly more mean­ing­ful to the av­er­age geo­met­ric to­po­lo­gist, and giv­ing us a slightly more to­po­lo­gic­al way to think of what the Seiberg–Wit­ten in­vari­ants are count­ing.

In­spired by Taubes’ near-sym­plect­ic vis­ion dis­cussed in the pre­ced­ing sec­tion, Auroux, Don­ald­son and Katzarkov [e17] gen­er­al­ized Don­ald­son’s Lef­schetz fibra­tion res­ult to show that every near-sym­plect­ic 4-man­i­fold, after blow­ing up, has the struc­ture of a broken Lef­schetz fibra­tion (BLF), which is like a Lef­schetz fibra­tion over \( S^2 \) but also al­lows for a 1-di­men­sion­al locus of sin­gu­lar­it­ies of a par­tic­u­lar mod­el, called in­def­in­ite folds. This 1-di­men­sion­al sin­gu­lar set is ex­actly the same zero locus where the near sym­plect­ic form van­ishes. Fol­low­ing our noses, we nat­ur­ally wondered next how to con­struct these BLF’s “ex­pli­citly” from, for ex­ample, a handle de­com­pos­i­tion of a 4-man­i­fold. In the end [3] we dis­covered that if we al­lowed both ori­ent­a­tion pre­serving and ori­ent­a­tion re­vers­ing loc­al mod­els for the Lef­schetz type sin­gu­lar­it­ies (we called the res­ult­ing fibra­tions broken achir­al Lef­schetz fibra­tions, or BALFs), then we could con­struct BALFs on all closed ori­ented 4-man­i­folds.

The con­struc­tion was sim­il­ar in spir­it to our con­struc­tion of near-sym­plect­ic forms: First we found a good way to split the giv­en 4-man­i­fold in­to two pieces on each of which we could con­struct par­tial fibra­tions and then we figured out the ap­pro­pri­ate bound­ary con­di­tions to gov­ern these fibra­tions on the sep­ar­at­ing 3-man­i­fold. (Ex­per­i­enced low-di­men­sion­al to­po­lo­gists will not be sur­prised that this bound­ary con­di­tion is the struc­ture of an “open book de­com­pos­i­tion”.) Then we mas­saged our con­struc­tions care­fully so as to ar­range that this bound­ary data agreed and we could glue the fibra­tions to­geth­er. As be­fore, it would be disin­genu­ous to de­scribe our con­struc­tion as ex­pli­cit be­cause of this last step, which passed from open book de­com­pos­i­tions to con­tact struc­tures by way of the Giroux cor­res­pond­ence [e14] and then ap­pealed again to Eli­ash­berg’s clas­si­fic­a­tion [e8] of over­twisted con­tact struc­tures.

Aside from this caveat about ex­pli­cit­ness or the lack there­of, an­oth­er thread the read­er may be pick­ing up is the in­creas­ing mix­ing of cat­egor­ies here: The study of al­most com­plex struc­tures, sym­plect­ic struc­tures and Lef­schetz fibra­tions already lies (a little bit un­com­fort­ably) some­where between com­plex al­geb­ra­ic geo­metry and dif­fer­en­tial to­po­logy. Throw­ing in circles along which new types of de­gen­er­a­tions arise, and in the fibra­tion case hav­ing both isol­ated com­plex type sin­gu­lar­it­ies as well as 1-di­men­sion­al de­cidedly non­holo­morph­ic sin­gu­lar­it­ies, and then al­low­ing the isol­ated sin­gu­lar­it­ies to flip ori­ent­a­tions, really starts to seem like a bit of a stretch and an awk­ward mix of per­spect­ives. The next phase in our col­lab­or­a­tion star­ted to clean this up.

The aux­il­i­ary struc­tures of rel­ev­ance here are, in a broad sense, stable smooth maps from man­i­folds of some di­men­sion to oth­er man­i­folds of lower di­men­sion. A map is stable if small per­turb­a­tions do not change its es­sen­tial qual­it­at­ive fea­tures; more pre­cisely, the ori­gin­al map and the per­turbed are equal after pre- and post-com­pos­ing with iso­top­ies of the do­main and range. Thus the func­tion \( y=x^2 \) is stable in the world of smooth maps from \( \mathbb{R} \) to \( \mathbb{R} \) while the func­tion \( y=x^3 \) is not. Stable maps from smooth man­i­folds to \( \mathbb{R} \) (and some­times to oth­er 1-man­i­folds such as the circle or a closed in­ter­val) are called Morse func­tions and have been tre­mend­ously use­ful tools for prob­ing the to­po­logy of smooth man­i­folds in gen­er­al, es­pe­cially when used in con­junc­tion with gradi­ent-like vec­tor fields to give handle de­com­pos­i­tions. Stable maps to di­men­sion 2 are also fairly well un­der­stood but have not been used as ex­tens­ively as Morse func­tions as a tool to probe the to­po­logy of man­i­folds.

Per­utz [e20] stud­ied the prob­lem of de­fin­ing, in the broken Lef­schetz fibra­tion set­ting, something ana­log­ous to the counts of pseudo­holo­morph­ic multi­sec­tions for Lef­schetz fibra­tions stud­ied by Ush­er, mo­tiv­ated by the pos­sib­il­ity that these would then again re­cov­er Seiberg–Wit­ten in­vari­ants, or at least be in­vari­ants even if one did not know that they agreed with preex­ist­ing in­vari­ants. To show dir­ectly that these counts, called Lag­rangi­an match­ing in­vari­ants, are in fact 4-man­i­fold in­vari­ants, and did not de­pend upon the choice of BLF, one would need to un­der­stand how to move from one BLF on a giv­en 4-man­i­fold to an­oth­er. In oth­er words, one needs not only ex­ist­ence res­ults for B(A)LFs, but also unique­ness res­ults.

While we were think­ing about this (work­ing to­geth­er at the Afric­an In­sti­tute of Math­em­at­ic­al Sci­ences in Muizen­berg, South Africa, prob­ably in 2007) we found out about Lekili’s in­sight­ful ob­ser­va­tion [e21] that if one wanted to con­nect two BLF’s by a 1-para­met­er fam­ily of smooth func­tions, one should first ob­serve that Lef­schetz sin­gu­lar­it­ies are ac­tu­ally not stable in the world of smooth maps. A small per­turb­a­tion in the world of smooth maps will make a Lef­schetz sin­gu­lar­ity in­to a much more com­plic­ated circle of sin­gu­lar­it­ies. Thus a gen­er­ic 1-para­met­er fam­ily of smooth func­tions con­nect­ing two Lef­schetz fibra­tions or BALFs should be ex­pec­ted to pass through func­tions that are much more gen­er­al and do not have any Lef­schetz sin­gu­lar­it­ies at all. The loc­al be­ha­vi­or of stable smooth maps from 4-man­i­folds to 2-man­i­folds has in fact been un­der­stood for a long time and Lekili’s pa­per [e21] has an ex­cel­lent ap­pendix that runs through the gen­er­al ma­chinery for un­der­stand­ing stable maps between vari­ous di­men­sions [e3] ap­plied in the case of di­men­sions 4 and 2. At least this is where I learned this ma­ter­i­al, Rob prob­ably ba­sic­ally had already ab­sorbed most of this by os­mos­is over the years and just needed a little re­mind­er from Lekili’s art­icle.

Lekili es­sen­tially answered the ques­tion of how to think about loc­al moves con­nect­ing one BALF to an­oth­er, but the key prob­lem was that in the in­ter­me­di­ate stages one might wander quite far away from the world of BALFs and move through maps that are noth­ing like small per­turb­a­tions of BALFs. In par­tic­u­lar, one might run in­to what are called def­in­ite folds, dis­cussed in more de­tail be­low. Wheth­er one could avoid def­in­ite folds is ana­log­ous to the ques­tion of wheth­er, in a 1-para­met­er fam­ily of func­tions con­nect­ing two giv­en Morse func­tions with the same num­ber of min­ima and max­ima, one can avoid in­tro­du­cing ex­tra min­ima or max­ima along the way. In gen­er­al this can be done, mod­ulo some ob­vi­ous counter­examples and low-di­men­sion­al ex­cep­tions. Be­cause of the ana­logy with Morse the­ory, Rob and I began call­ing stable maps to di­men­sion 2 Morse 2-func­tions, think­ing of them as vaguely like a 2-cat­egory ver­sion of Morse func­tions, whatever that might mean. (Here we were very much in­spired by con­ver­sa­tions with Peter Teich­ner at MSRI in the spring of 2010.)

The key idea of a Morse 2-func­tion is that loc­ally a Morse 2-func­tion \( F \) on an \( n \)-man­i­fold looks like a gen­er­ic 1-para­met­er fam­ily \( f_t \) of Morse func­tions on an \( (n-1) \)-man­i­fold, so that there are loc­al co­ordin­ates so that \( F(t,p) = (t,f_t(p)) \) where \( t \) is a single time para­met­er, \( p \) is an \( (n-1) \)-di­men­sion­al “spa­tial” co­ordin­ate, and \( f_t \) is a gen­er­ic path of func­tions con­nect­ing two Morse func­tions. However, glob­ally there is no well-defined time dir­ec­tion, either in do­main or range. Gen­er­ic 1-para­met­er fam­il­ies of Morse func­tions will be hon­est Morse func­tions for all but fi­nitely many times, and at fi­nitely many times will ex­per­i­ence births or deaths of pairs of crit­ic­al points, or the co­in­cid­ence of two crit­ic­al points hav­ing the same crit­ic­al value at an in­stant. The tracks of the crit­ic­al points for the hon­est Morse func­tions are called folds, and are 1-di­men­sion­al in do­main and range, while the birth/death events are called cusps; the co­in­cid­ences of hav­ing two crit­ic­al points with the same crit­ic­al value are folds whose im­ages in the range cross. The gen­er­ic be­ha­vi­or of ho­mo­top­ies between Morse 2-func­tions is ex­actly loc­ally modeled on the gen­er­ic be­ha­vi­or of ho­mo­top­ies between ho­mo­top­ies between Morse func­tions, in oth­er words the moves of “Cerf the­ory”.

If the pre­ced­ing para­graph did not mean much to the read­er, the ba­sic idea is well il­lus­trated with a pic­ture of a Morse 2-func­tion on a sur­face. Fig­ure 6 shows a Morse 2-func­tion on a tor­us. In fact, any time one draws a pic­ture of a sur­face on a piece of pa­per, one is of course present­ing a map from that sur­face to \( \mathbb{R}^2 \) and, as­sum­ing gen­er­i­city, this will be a Morse 2-func­tion. The folds are lit­er­ally the places where the sur­face folds over, and the cusps are where folds “switch dir­ec­tions” in some sense; these are all clearly vis­ible in this il­lus­tra­tion. The preim­age of a nonsin­gu­lar point is an even num­ber of points in the tor­us, and the num­ber of these points jumps by 2 when cross­ing a fold. The only dif­fer­ence in high­er di­men­sions in that dif­fer­ent di­men­sions and codi­men­sions can fold in op­pos­ite dir­ec­tions along a fold, and the preim­ages of nonsin­gu­lar points are high­er di­men­sion­al sub­man­i­folds, not col­lec­tions of points. In di­men­sion 4, the preim­ages of points are sur­faces, and the to­po­logy of these sur­faces changes as one crosses a fold.

Note that the in­dex of a fold ranges from 0 to \( n-1 \), but is only well-defined up to switch­ing \( k \) with \( n-1-k \). A fold of in­dex 0 (equi­val­ently \( n-1 \)) is called a def­in­ite fold and all oth­er folds are called in­def­in­ite. Thus on 4-man­i­folds there are only really two types of folds: def­in­ite in­dex 0 (equi­val­ently 3) folds and in­def­in­ite in­dex 1 (equi­val­ently 2) folds. (On a 2-man­i­fold, all folds are def­in­ite.) One reas­on def­in­ite folds in di­men­sion 4 might be un­desir­able is that they in gen­er­al lead to dis­con­nec­ted fibers, since cross­ing a def­in­ite fold in the in­dex 0 dir­ec­tion cre­ates a new \( S^2 \)-com­pon­ent of the fiber. This (and \( S^2 \)-fibers in gen­er­al per­haps) is bad from a sym­plect­ic geo­metry and in­vari­ant con­struct­ing per­spect­ive, as ex­plained to us by Kat­rin Wehrheim, an­oth­er ma­jor mo­tiv­at­or for us in our early work in this sub­ject.

The up­shot is that we showed [4] how to con­struct in­def­in­ite, fiber-con­nec­ted Morse 2-func­tions on a giv­en \( n \)-man­i­fold in a giv­en ho­mo­topy class of maps, when \( n > 3 \) and a nat­ur­al \( \pi_1 \) con­di­tion is sat­is­fied, and we also showed that any two such Morse 2-func­tions can be con­nec­ted by a gen­er­ic ho­mo­topy main­tain­ing the in­def­in­ite and fiber-con­nec­ted prop­er­ties, again when \( n > 3 \). Of course, all along we were primar­ily in­ter­ested in the case \( n=4 \) and, hav­ing settled this ques­tion, we now star­ted to think ser­i­ously about what to do with Morse 2-func­tions in gen­er­al on smooth 4-man­i­folds, how to put them in­to par­tic­u­larly nice forms, and how to use them to ap­pro­pri­ately probe the to­po­logy of the man­i­folds in­volved.

I star­ted my po­s­i­tion at the Uni­versity of Geor­gia (UGA) in Au­gust 2011. One thing Rob was al­ways fant­ast­ic about was trav­el­ing to vis­it me wherever I ended up, un­der­stand­ing that my fam­ily life with three kids made it harder for me to up and travel at the drop of a hat. And Rob had a long time con­nec­tion to UGA go­ing back to the early days of the Geor­gia To­po­logy Con­fer­ence, so he star­ted vis­it­ing me at UGA pretty reg­u­larly (and mak­ing sure to com­bine each such vis­it with some so­cial time with old re­tired friends Jim Cantrell and John Hollings­worth). Over the course of a few vis­its in late 2011 and early 2012 we were busy draw­ing pic­tures of \( \mathbb{R}^2 \)-val­ued Morse 2-func­tions on ho­mo­topy 4-spheres arising from bal­anced present­a­tions of the trivi­al group not known to be An­drews–Curtis trivi­al­iz­able. Our grand hope of course was to find an in­vari­ant that could show that these ho­mo­topy 4-spheres were not dif­feo­morph­ic to \( S^4 \), and we had an idea that would in­volve count­ing cer­tain sur­faces with bound­ary on the folds. (We called these sur­faces flow charts be­cause they would be swept out by flow lines of gradi­ent-like vec­tor fields in loc­al charts; this is a loose end idea that nev­er panned out for us, just in case the story was seem­ing too tidy with sus­pi­ciously few false starts and dead ends.)

In the pro­cess we de­veloped a very sys­tem­at­ic and stand­ard­ized way to or­gan­ize the im­age of a \( \mathbb{R}^2 \)-val­ued Morse 2-func­tion and, sud­denly, one day tri­sec­tions jumped out at us! In hind­sight so much of it is ob­vi­ous but at the time it seemed some­how un­usu­al and dra­mat­ic. The key point is that we were busy build­ing Morse 2-func­tions “from left to right”, start­ing from handle de­com­pos­i­tions of 4-man­i­folds, with the 0- and the 1-handles at the left con­trib­ut­ing a very stand­ard part of the Morse 2-func­tion, the 3- and 4-handles at the right con­trib­ut­ing a mirrored stand­ard piece, and the 2-handles in the middle do­ing something in­ter­est­ing. Then sud­denly tri­sec­tions jumped out at us when we real­ized one day in my of­fice at UGA that we could split things a little dif­fer­ently by sep­ar­at­ing the cusps in­to three groups.

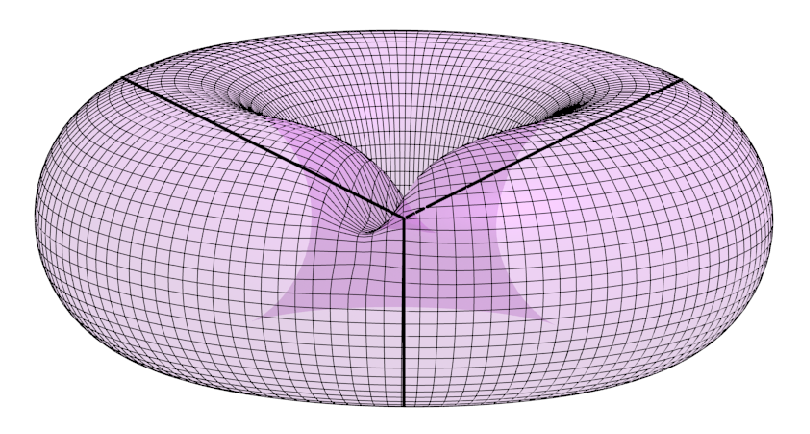
The ba­sic idea is well il­lus­trated by a half-di­men­sion­al car­toon. (I be­lieve that Rob taught all of his stu­dents and col­lab­or­at­ors the value of the half-di­men­sion­al ana­logy when work­ing in di­men­sion 4.) In Fig­ure 7, we show a se­quence of Morse 2-func­tions on the tor­us, each ob­tained by per­form­ing some pro­ced­ure to the pre­ced­ing one, and end­ing with one which might seem un­ne­ces­sar­ily com­plic­ated. However, if one then tri­sects the tor­us us­ing the last Morse 2-func­tion, as il­lus­trated in Fig­ures 8 and 9, we see that in fact the tor­us is de­com­posed in­to three disks (care­ful in­spec­tion shows that these disks are hexagons), and this is the ba­sic “tri­sec­tion” of \( T^2 \). We es­sen­tially mim­ic this pro­ced­ure with more care in di­men­sion 4 to pro­duce tri­sec­tions of ar­bit­rary 4-man­i­folds.

We re­leased two ver­sions of our pa­per on the arX­iv with quite a gap between them and a sig­ni­fic­ant dif­fer­ence. One of Rob’s life les­sons for me was that if you prove an ex­ist­ence the­or­em then you should prove a unique­ness the­or­em. Our first ver­sion (May 2012) only had the ex­ist­ence res­ult and then it took us more than a year to nail down the unique­ness res­ult (Septem­ber 2013). Some­where in between those two dates was a hard­work­ing ses­sion at the Max Planck In­sti­tute for Math­em­at­ics in Bonn, in which An­dras Stip­sicz had sev­er­al help­ful com­ments about how to pro­ceed with unique­ness. Once we had the unique­ness res­ult it was stu­pidly ob­vi­ous, and the (for us) really start­ling fact was just how closely it mirrored the unique­ness res­ult for Hee­gaard split­tings of 3-man­i­folds.

Hav­ing “dis­covered” tri­sec­tions, it did also be­come clear to us that in many ways we were ob­vi­ously re­dis­cov­er­ing things oth­ers already knew quite well. Of par­tic­u­lar note is the fact that Birman and Craggs [e4] es­sen­tially already thought about tri­sec­tions of 4-man­i­folds from the per­spect­ive of map­ping class groups of sur­faces, us­ing the term tri­ad­ic 4-man­i­folds. (At least, this term ap­pears in a sec­tion head­ing in that pa­per, al­though it nev­er ap­pears in the ac­tu­al tex­tu­al body of the pa­per. Per­haps they had an in­tu­ition that there was something more go­ing on with these struc­tures on 4-man­i­folds or even, as is so of­ten the case, knew much more than they wrote in their pa­per.) More re­cently, Os­zváth and Szabó were very ob­vi­ously work­ing with these struc­tures in the guise of Hee­gaard triples [e19] Our main ex­ist­ence res­ult is more or less im­pli­cit in Os­zváth and Szabó’s work, and one could in­ter­pret the thrust of our work as be­ing to un­der­stand the raw to­po­lo­gic­al im­plic­a­tions of the fact that every 4-man­i­fold can be de­scribed by a Hee­gaard triple, rather than simply view­ing Hee­gaard triples as a tool to un­der­stand­ing vari­ous maps in Hee­gaard Flo­er the­ory. However the unique­ness res­ult, and the study of tri­sec­tions as ac­tu­al de­com­pos­i­tions of 4-man­i­folds, uni­fies the sub­ject and sets the stage for many in­ter­est­ing dir­ec­tions of study.

Many oth­er math­em­aticians have made strik­ing con­tri­bu­tions to the the­ory of tri­sec­tions since our first pa­per. Each of this con­tri­bu­tions is worth a lengthy dis­cus­sion, but since we are fo­cus­ing on Rob Kirby’s work here, I’ll briefly de­scribe the most im­port­ant ex­ten­sion to the the­ory that Rob and I were in­volved in, namely the de­vel­op­ment of group tri­sec­tions [6] in col­lab­or­a­tion with Aaron Ab­rams.

One of the first things we thought about with tri­sec­tions was un­der­stand­ing how much in­form­a­tion about a smooth 4-man­i­fold one re­tains when ap­ply­ing al­geb­ra­ic to­po­lo­gic­al func­tors to a tri­sec­tion, (to all the pieces and their in­ter­sec­tions and the vari­ous in­clu­sion maps). Since Freed­man taught us that in some spe­cial cases the al­geb­ra­ic to­po­logy of 4-man­i­folds seems to ba­sic­ally re­cord homeo­morph­ism type, we ex­pec­ted some­how that by passing from smooth tri­sec­tions to the al­geb­ra­ic to­po­lo­gic­al shad­ows of tri­sec­tions we would pass from smooth in­form­a­tion to to­po­lo­gic­al in­form­a­tion and then be able to un­der­stand something about how tri­sec­tions of homeo­morph­ic but not dif­feo­morph­ic man­i­folds are re­lated. In fact it turned out, after Aaron Ab­rams re­minded Rob and me of some ba­sic facts from 3-man­i­fold to­po­logy, that the most ba­sic al­geb­ra­ic to­po­logy func­tor of all, \( \pi_1 \), loses no in­form­a­tion at all! The in­clu­sion maps between the triple in­ter­sec­tions, double in­ter­sec­tions, single pieces and total man­i­fold mak­ing up a tri­sec­tion fit in­to a cube of spaces and, when the \( \pi_1 \) func­tor is ap­plied, one gets a cube of groups in­volving one sur­face group, six free groups, and the fun­da­ment­al group of the total 4-man­i­fold and from this cube of groups one can com­pletely re­cov­er the smooth 4-man­i­fold and its tri­sec­tion.

We thus defined a group tri­sec­tion of a giv­en group \( G \) as a cube of groups and ho­mo­morph­isms between them such that at one ver­tex we have the fun­da­ment­al group of a closed, ori­ented sur­face, at the op­pos­ite ver­tex we have the group \( G \), and at the six in­ter­me­di­ate ver­tices we have free groups. The maps all flow from the sur­face group in the dir­ec­tion of \( G \), all the maps are sur­ject­ive, and all the six faces of the cube are pushouts. The main res­ult is that a tri­sec­ted group gives a tri­sec­ted 4-man­i­fold and vice versa. This is strik­ing; for ex­ample, a tri­sec­ted group car­ries with it an in­teg­ral quad­rat­ic form, namely the in­ter­sec­tion form of the as­so­ci­ated 4-man­i­fold.

The cru­cial piece of 3-man­i­fold to­po­logy that Aaron re­minded us of is the fol­low­ing “stand­ard fact” (for a proof see [e12]): Any sur­ject­ive group ho­mo­morph­ism from the fun­da­ment­al group of a genus \( g \) sur­face to a free group of rank \( g \) arises as the map in­duced by the in­clu­sion of the sur­face as the bound­ary of a genus \( g \) handle­body, and the handle­body filling of that sur­face is uniquely de­term­ined by the group sur­jec­tion. This, to­geth­er with Lauden­bach and Poénaru’s res­ult [e2], that every dif­feo­morph­ism of a con­nec­ted sum of \( S^1 \times S^2 \)s ex­tends across a bound­ary con­nec­ted sum \( S^1 \times B^3 \)s, is really all you need to prove that a tri­sec­ted 4-man­i­fold can be com­pletely re­covered from the as­so­ci­ated group tri­sec­tion.

In fact, everything we did is fore­shad­owed in, and in­spired by, John Stallings’ fam­ous pa­per [e1] “How not to prove the Poin­caré con­jec­ture”, which be­gins with the mem­or­able line “I have com­mit­ted the sin of falsely prov­ing Poin­caré’s Con­jec­ture. But that was in an­oth­er coun­try and un­til now, no one has known about it.” One con­sequence of the dic­tion­ary between tri­sec­tions of groups and tri­sec­tions of 4-man­i­folds is that the smooth 4-di­men­sion­al Poin­caré con­jec­ture can be re­for­mu­lated en­tirely group the­or­et­ic­ally, just as Stallings re­for­mu­lated the 3-di­men­sion­al Poin­caré con­jec­ture purely group the­or­et­ic­ally. I ar­gued un­suc­cess­fully with my coau­thors in fa­vor of titling our group tri­sec­tions pa­per “How not to prove the smooth 4-di­men­sion­al Poin­caré con­jec­ture”. I sus­pect that Rob, in par­tic­u­lar, re­jec­ted my pro­pos­al be­cause, deep down, he is a fun­da­ment­ally op­tim­ist­ic math­em­atician and, wheth­er the con­jec­ture is true or false, he’s al­ways will­ing to con­sider the pos­sib­il­ity that some new idea really might be the right way for­ward to set­tling the ques­tion once and for all.

Dav­id Gay was born in 1968 in Sua­coco County in up­coun­try Liber­ia, grew up in Liber­ia, Eng­land, Leso­tho and Mas­sachu­setts, ended up with a PhD in Math­em­at­ics from UC Berke­ley in 1999, and has been a pro­fess­or at the Uni­versity of Geor­gia since 2011. He has thought about to­po­logy and taught math­em­at­ics at many levels around the world, with postdoc­tor­al po­s­i­tions at the Uni­versity of Ari­zona, the Nankai In­sti­tute of Math­em­at­ics, and the Uni­versity of Que­bec, a Seni­or Lec­ture­ship at the Uni­versity of Cape Town, and, most re­cently, a vis­it­ing po­s­i­tion as Hirzebruch Re­search Chair at the Max Planck In­sti­tute of Math­em­at­ics in Bonn in 2019–20.