by Cathleen S. Morawetz
It seems impossible to recall when I first met Olga Taussky-Todd. She was an old Göttingen friend of both Courant and Friedrichs, and she spent a year with John at the fledgling Courant Institute in the early 1950s, but I feel sure I met her before then. I also heard about her from my parents, who had known Olga’s Irishman, John Todd, for a long time.
I recall two conversations with Olga. In the first one, very long ago, I asked Olga about her war work on flutter problems (flutter is caused by the resonance interaction between an airfoil and the gas flowing past it). But she was no longer interested in the subject, and my interest was also mostly gone. By then, algebra was her main concern, and her great arena.
Our later talk took place around 1968. I had just been appointed to the AMS Committee on Women. I used a trip west to ask all the women mathematicians I knew who were roughly my age about their careers and positions. It was a sobering mission as none of the women, except the statistician Betty Scott, had the standard academic job I had.
Olga insisted our talk was off the record, and so it shall essentially remain. However, it was an opportunity for her to put away her wonderful smile and air her complaints. Her greatest difficulties had come from being both Jewish and a woman. Her early year in Bryn Mawr had been difficult, and not having a regular position at Caltech rankled within her. But her beloved work in mathematics saved her.
I shall talk now about my own early years in mathematics. I worked on my first scientific problem during 1943–1944. I was measuring the muzzle velocity of shells for the Inspection Board of the United Kingdom and Canada. I was there because I had wanted to be a radar officer in the Navy, as my male fellow students became, but I was told I would have to start with boot-training, scrubbing floors, etc. (That made me angry!)
I found an error in a graph that was used whenever the weather was bad. Fixing it up was great fun. I will not bore you with the details, but it showed me that a little bit of undergraduate mechanics could get you something useful. Well, useful, although maybe the old graph had pragmatic information that I had not used. I owe it to my boss, Malcolm Macphail, a very able physicist, for making me write it up.
At the Inspection Board, I had my first exposure to visible prejudice — against my French–Canadian coworkers. So I retained a lifelong sympathy for their nationalist reaction as I did for my parents’ Irish nationalism, that is, nationalism tempered by understanding and goodwill.
My second problem in mathematics was a master’s thesis at MIT in elasticity. It was in fact a rather unmanageable problem in flutter theory. I did not really understand it or find it interesting. I am glad to see that master’s theses in math are mostly replaced today by learning more mathematics.
The atmosphere at MIT, though essentially male, was not at all hostile to women. I was there because Caltech took no women and Harvard only put them thorough via Radcliffe, which I found offensive. However, I did find at MIT, as I have found almost everywhere, men whose attitude toward professional women is best told through a story of today:
A few weeks ago I was traveling in a remote part in the west of Ireland, where I met a country man. He asked me if it was true that I “was in the higher education.” I replied that I was a professor of mathematics, to which he responded, “It would not do a man to make some kind of failure and you around.”
On to my third mathematical problem. I married and moved to New York in 1946 to the group to the working with Courant, Friedrichs, and Stoker. They had worked together on military problems during the war. For better or worse, since the time of Archimedes’s catapult, the military has been the source of very interesting problems in mechanics, and I was engaged to work for and be supported by an ONR contract. The job, shades of Olga’s past at Göttingen, was to fix the English and not tamper with the mathematics of Courant and Friedrichs’s great book, Supersonic Flow and Shock Waves,1 which was being made out of a previously classified set of notes, written during the war. This had been, I now think, the greatest wartime contribution of that group. Except for another year at MIT, I spent the rest of my career at NYU as Courant’s group evolved.
Friedrichs gave me, from time to time, spin-off problems, but mostly I edited. I learned fluid dynamics, at the same time complaining about the obscurity of Friedrich’s writing and the shortcuts Courant introduced to make the book more readable.
My first “published” contribution was an appendix to a paper using stationary phase. I learned stationary phase that way. For me, doing, not reading, has been the best way to learn. The paper was by Friedrichs and Hans Lewy on flow near a dock [e2]. My job was to find the second term in an asymptotic expansion. The first was of course found by Friedrichs and Lewy, and, I might add, no estimate of the error was made by me or anyone else.
I found that I had some skill and got great pleasure out of the manipulation of the necessary formulas. Friedrichs urged me to be a coauthor but out of some perverse vanity I declined. This was 1948, and the paper was published in one of the first issues of Communications.2 I was duly credited in the text.
By then I had one child. Courant had a big ONR grant. He generously allowed me to work part-time. No timetable was mentioned except that I should take my orals as soon as possible, which I did. I started to work on a thesis in quantum mechanics, Friedrichs’s lifelong love, but by that time I had one-and-a-half children, and Friedrichs and Courant persuaded me to convert one of my Navy problems into a thesis.
The thesis was a study of the stability of a spherical implosion under a perturbation of the initial conditions, while preserving spherical symmetry. To me, the application was to collapsing stars, and in fact the interest today would again be in the stars. The military application to igniting the first nuclear bombs was unknown to Friedrichs and to me. It was not made public until the spy trial of the Rosenbergs in 1952.
I never published my thesis because it was disappointingly incomplete. I know now that almost every thesis has unfinished business, and one should think twice before not publishing one’s thesis. The underlying problem is a perturbation of a particular solution of Euler’s equations that is spherically symmetric. Thus the equations are for \( u \) radial velocity, \( \rho \) density, and \( p \) pressure, respectively. The radial distance is \( r \). the equations are \begin{equation*} \begin{aligned} \rho_t+u\rho_r+\rho\Big(u_r+\frac{2u}{r}\Big) &=0 &&\mathrm{Mass}\\ u_t+uu_r+\frac{1}{\rho}p_r &=0 &&\mathrm{Momentum}\\ (p\rho^{-\gamma})_t+u(p\rho^{-\gamma})_r &=0 &&\mathrm{Entropy} \end{aligned} \end{equation*}
The exponent \( \gamma \) is the ratio of the specific heats. The special solutions are of the form \( u=r/tU(\eta) \) etc. with \( \eta=r^{-\lambda}t \). The pictures are in Figure 1.
The problem reduces to solving a single autonomous ordinary differential equation: \begin{equation*} \frac{dC^2}{dU}=\frac{B(U,C)}{A(U,C)} \end{equation*}
\( C \) is essentially the sound speed. There are lots of lovely singular points where \( A=B=0 \). The parameter \( \lambda \) has to be chosen so that a solution exists which represents an implosion.
This solution was found during World War II by v. Neumann and others at Los Alamos, G. I. Taylor in Britain, and, of all things, by G. Guderley in Germany, where it was published during the war in the open literature [e1]. This literature was combed by scientists after the war, and the result was described in Courant and Friedrichs’s book.
To look at stability we perturb around this solution and look for complex solutions of the resulting linear equation that grow exponentially in time, like \( \exp(k,t) \) with \( \operatorname{Re} k > 0 \). I succeeded in reducing the problem to studying a second-order ordinary differential equation (o.d.e.) with real coefficients depending on \( \eta \); i.e., \( r^{-\lambda}t \) and the complex parameter \( k \). It was singular where \( \eta=0 \); i.e., \( t=0 \), the moment of reflection. I had to prove there were no eigenvalues with \( \operatorname{Re}k > 0 \). But \( k \) appeared in an odd non-standard way and, even worse, the equation was singular at \( \eta=0 \) in a manner not considered in the then standard works of Langer on o.d.e. Langer’s results worked for “something” less than zero. I needed equals zero. Torture! I tried hand computation on a Marchand calculator — too time-consuming and inaccurate. Later asymptotic theory for such equations was worked out, but too late for me. I never looked back. What was really wrong? (1) The problem had too many cliffhangers for a thesis. (2) I had too many duties as a mother of two. But I got my degree or, as Courant liked to say, my union card.
The next problems were similar: singular o.d.e. with a parameter. But this time they were solvable. I was at MIT working for C. C. Lin and paid for part-time from NASA grant. I wrote my first two papers, and they were published [1], [2].
Even before this, Courant invited me to come back to his institute, again to be supported by ONR. For the next six years, I worked on an assortment of problems, mostly on transonic flow. Everything worked well, more or less. And I had two more children.
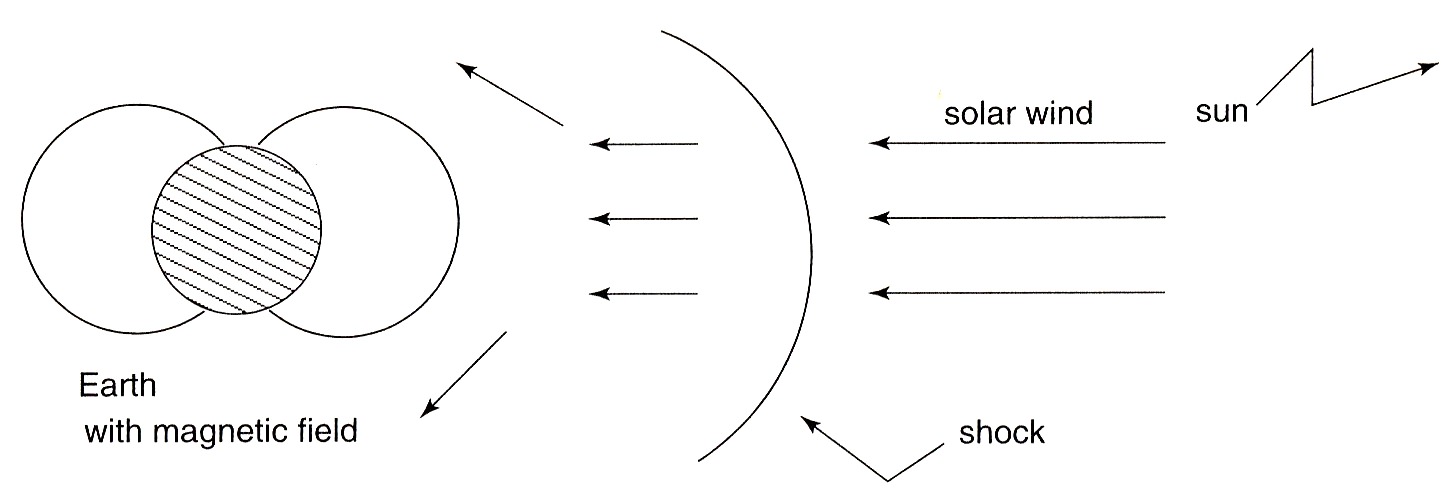
Courant, around 1956 I think, proposed that I join Harold Grad’s group in magneto hydrodynamics (MHD) and plasma physics. He enticed me with the prospect of helping to solve the world’s energy problem through thermonuclear fusion. Still an open question to say the least! But it was a golden lode for problems, from nonlinear hyperbolic partial differential equations in MHD to statistical mechanics without collisions. I nibbled away for twelve years, but the rewards were all modest. As an example, here in Figure 2 is a plasma problem, connected actually to the solar wind as well as thermonuclear fusion. An ionized gas or plasma, the solar wind flows toward earth. The magnetic field of the earth repels the wind. Because of the high speed of the wind, a shock, like the bow shock in front of a supersonic airplane, is formed between the earth and the sun. Question: What is the mechanism for the shock?

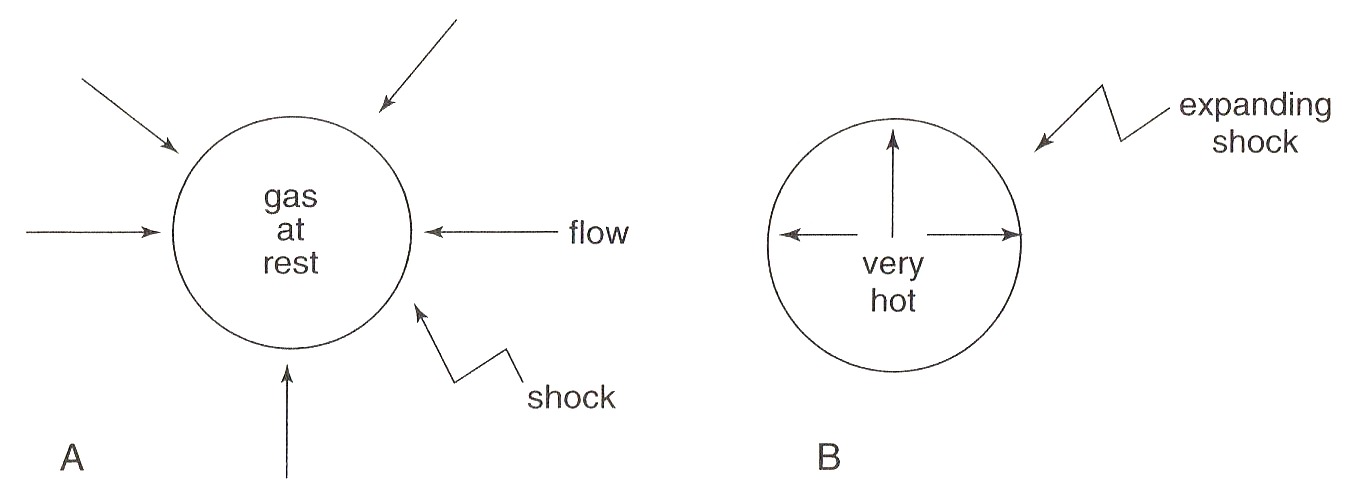
In gas dynamics you argue that the shock (jump in flow quantities) is smoothed out by adding viscous terms to the questions. In Figure 3, a one-dimensional model, the width of the transition goes to infinity with the viscosity or mean free path. I do not know what the mechanism is for the solar wind, but for the controlled thermonuclear fusion setup for making energy it is enormous. If there is going to be a realistic shock limit, there has to be a better mechanism. I did create a crude model, but this is still today an interesting unsolved problem involving asymptotics and statistical mechanics and with lots of room for new ideas.
Aside from untreatable mathematics problems, and that’s the way most problems from physics are, the problem of those years was that I was moving forward professionally only very slowly. I had successfully avoided teaching. I considered that I could not raise four children, do research, and teach, so I settled for the first two. I hoped to get a regular position when my youngest child went to school. In 1957, six years after my Ph.D., Courant offered me an assistant professorship in the Institute. I accepted knowing that I might not have a second chance. So in 1957 I stopped being a hybrid, part-time research worker cum postdoc and became a regular faculty member.
Those six early years gave me a very special start. I wish something like those opportunities were more available to women — as I like to call them, those valiant women — who have to choose between having children and risking tenure, or getting tenure and risking not having children.