Celebratio Mathematica

The work of Cath­leen Mor­awetz on tran­son­ic flu­id flow and the un­der­ly­ing PDEs of mixed el­lipt­ic-hy­per­bol­ic type spanned her ca­reer. Here we de­scribe her earli­est work. Be­gin­ning in the mid 1950s, Mor­awetz began work­ing on tran­son­ic flow prob­lems through her in­ter­ac­tions with Kurt O. Friedrichs and Lip­man Bers. This prob­lem area was ripe for the unique blend of joy­ous in­genu­ity and prac­tic­al tenacity which char­ac­ter­ized her ap­proach to hap­pily do­ing math­em­at­ics in or­der to say something about a real world prob­lem. Mor­awetz quickly made a name for her­self by giv­ing a math­em­at­ic­al an­swer to an im­port­ant en­gin­eer­ing ques­tion in tran­son­ic air­foil design.

Mor­awetz peri­od­ic­ally re­turned to this area with bursts of pro­ductiv­ity that res­ul­ted in fun­da­ment­al con­tri­bu­tions over the next five dec­ades. The photo of Mor­awetz in 1958 shows the happy face that Mor­awetz would dis­play when dis­cuss­ing what in­ter­ested her most. It was with the same gentle smile and glint in the eyes that she might also show her warm tough­ness and at­tach­ment to phys­ic­al rel­ev­ance when li­quid­at­ing a night’s cal­cu­la­tions of a col­lab­or­at­or with a phrase like: “You know, the solu­tions should not really be­have this way. Let’s change the equa­tion.”

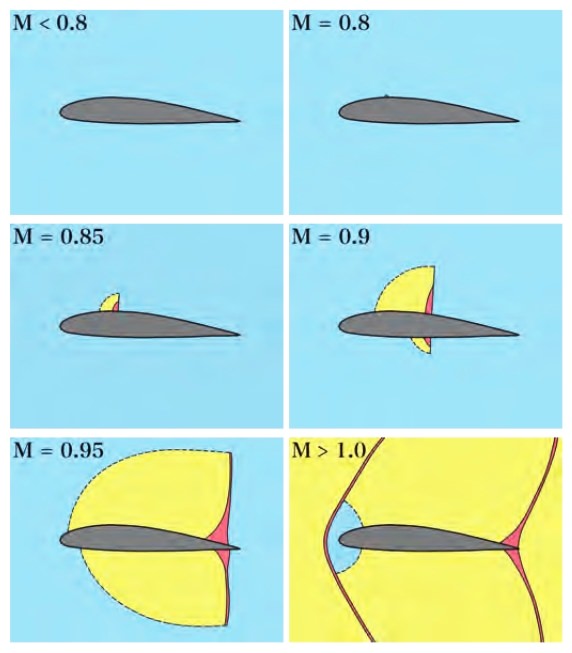
In aero­dy­nam­ics, a ba­sic ques­tion is: How does one fly at a re­l­at­ively high speed, with re­l­at­ively low cost and re­l­at­ively low eco­lo­gic­al dam­age? In Mor­awetz’s 1982 art­icle in the Bul­let­in of the AMS, she de­scribed the prob­lem as fol­lows. The sci­ence of flight de­pends on the re­l­at­ive speed of the air­craft with re­spect to the speed of sound in the sur­round­ing air. At re­l­at­ively low speeds, the sub­son­ic range, one can “sail” by design­ing wings to “get as much as pos­sible of a free ride” from the wind. At very high speeds, the su­per­son­ic range, one needs “rock­et propul­sion” to over­come the drag pro­duced by shocks that in­vari­ably form (the son­ic boom). The goal of study­ing tran­son­ic flow is to find a com­prom­ise which al­lows for “sail­ing” ef­fi­ciently “near the speed of sound.” Shocks pro­duce drag, which in­creases fuel con­sump­tion and hence in­creases cost. As seen in Fig­ure 7, shocks (colored red) be­gin to ap­pear on air­foils in wind tun­nels when the up­stream ve­lo­city is be­low, but near the speed of sound.

The 2-D ir­rota­tion­al, sta­tion­ary, com­press­ible and is­en­trop­ic flow of air about a pro­file \( P \) is gov­erned by an equa­tion for the po­ten­tial \( \phi(x, y) \) whose gradi­ent is the ve­lo­city field of the flu­id with vari­able dens­ity \( \rho \): \begin{equation} \label{seventeen} (c^2 - \varphi^2_x) \varphi_{xx} - 2\varphi_x \varphi_y \varphi_{xy} + (c^2 - \varphi^2_y ) \varphi_{yy} = 0. \end{equation} The nat­ur­al bound­ary con­di­tion is to have nor­mal de­riv­at­ive \begin{equation} \label{eighteen} \frac{\partial\varphi}{\partial n} = 0 \quad\text{on } \partial P. \end{equation} The nature of the flow is de­term­ined by the loc­al Mach num­ber \( M = q/c \) where \( q = |\nabla \varphi| \) is the flow speed and \( c > 0 \) is the loc­al speed of sound defined by \( c^2 = \partial p/\partial \rho \), where the adia­bat­ic pres­sure dens­ity re­la­tion in air is \( p = p(\rho) \sim \rho^{\gamma} \) with \( \gamma \approx 1.4 \). Ob­serve that equa­tion \eqref{seventeen} is of the form \[ A\varphi_{xx} - 2B\varphi_{xy} + C\varphi_{xx}. \] It is el­lipt­ic when \[ AC - B^2 > 0, \] which oc­curs at points where the flow is sub­son­ic \( (q < c) \). It is hy­per­bol­ic when \[ AC - B^2 < 0, \] which oc­curs at points where the flow is su­per­son­ic \( (q > c) \) (see Fig­ure 7). A tran­son­ic flow hap­pens when there are both sub- and su­per­son­ic re­gions and the equa­tion \eqref{seventeen} is of mixed el­lipt­ic-hy­per­bol­ic type.

The pres­ence of shocks in su­per­son­ic re­gions cor­res­ponds to drastic changes in air dens­ity and pres­sure com­ing from the com­press­ib­il­ity, and these large pres­sure changes propag­ate at su­per­son­ic speeds, res­ult­ing in a shock wave which typ­ic­ally has a small but fi­nite thick­ness. In Fig­ure 7, the shock wave re­gion is de­pic­ted in red. The ve­lo­city field \( \nabla\varphi \) gov­erned by \eqref{seventeen} will ex­per­i­ence jump dis­con­tinu­it­ies as one crosses the shock wave. One can use the pres­ence of such dis­con­tinu­it­ies to de­tect the pres­ence of shocks. The math­em­at­ic­al de­scrip­tion of shocks re­quires a sep­ar­ate ana­lys­is of en­tropy ef­fects, where equa­tion \eqref{seventeen} has broken down.

By the time of the Third In­ter­na­tion­al Con­gress for Ap­plied Mech­an­ics in 1930, a lively de­bate centered around the ques­tion: Do tran­son­ic flows about a giv­en air­foil al­ways, nev­er, or some­times pro­duce shocks? In par­tic­u­lar, is it pos­sible to design a vi­able air­foil cap­able of shock-free flight at a range of tran­son­ic speeds? Con­trast­ing evid­ence was presen­ted at the con­gress which led many aero­dy­nam­icists to take op­pos­ing views. G. I. Taylor presen­ted con­ver­gent Rayleigh series ex­pan­sions for the ve­lo­city po­ten­tial of some smooth tran­son­ic flows, while A. Buse­mann presen­ted the res­ults of wind tun­nel ex­per­i­ments that in­dic­ated the pres­ence of a lot of shocks. World War II moved at­ten­tion to rock­et propul­sion. An an­swer would await the work of Mor­awetz in the 1950s. It was a case of “math­em­at­ics com­ing to the res­cue.”

In a series of pa­pers pub­lished in 1956–58 in Comm. Pure Ap­pl. Math., Mor­awetz gave a math­em­at­ic­al an­swer by prov­ing that shock-free tran­son­ic flows are un­stable with re­spect to ar­bit­rar­ily small per­turb­a­tions in the shape of the pro­file. Her the­or­em says that even if one can design a vi­able pro­file cap­able of a shock-free tran­son­ic flow, im­per­fec­tion in its con­struc­tion will res­ult in the form­a­tion of shocks at the design speed.

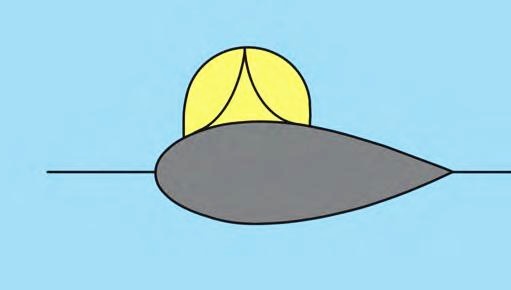
Mor­awetz’s proof in­volved two ma­jor steps. First, she de­term­ined the cor­rect bound­ary value prob­lem sat­is­fied the per­turb­a­tion of the ve­lo­city po­ten­tial in the hodo­graph plane where a hodo­graph trans­form­a­tion lin­ear­izes the PDE \eqref{seventeen} and sends the known pro­file ex­ter­i­or in­to an un­known do­main. Then, us­ing care­fully tailored in­teg­ral iden­tit­ies, she proved a unique­ness the­or­em for reg­u­lar solu­tions of the trans­formed PDE with data pre­scribed on only a prop­er sub­set of the trans­formed bound­ary pro­file, which says that the trans­formed prob­lem is over­de­termined and no reg­u­lar solu­tions ex­ist. Mor­awetz ex­ten­ded this res­ult to in­clude fixed pro­files but fi­nite per­turb­a­tions in \( q_{\infty} \), and the ex­ten­sion to non­sym­met­ric pro­files was car­ried out by L. Pamela Cook (In­di­ana Univ. Math. J., 1978).

Cath­leen Mor­awetz’s early work on tran­son­ic flow both trans­formed the field of mixed-type par­tial dif­fer­en­tial equa­tions and served as ex­cel­lent pub­li­city for math­em­at­ics. Com­ment­ing on the tran­son­ic con­tro­versy in 1955, the cel­eb­rated aero­dy­nam­icist Theodore von Kármán ob­served: “…the math­em­atician may ex­actly prove ex­ist­ence and unique­ness of solu­tions in cases where the an­swer is evid­ent to the phys­i­cist or en­gin­eer…On the oth­er hand, if there is really ser­i­ous doubt about the an­swer, the math­em­atician is of little help.” Mor­awetz’s sur­pris­ing the­or­em on the nonex­ist­ence of smooth flows was a cheer­ful re­sponse to von Kármán’s well-in­ten­tioned chal­lenge.

Hav­ing settled the en­gin­eer­ing ques­tion about the “ex­cep­tion­al nature” of shock-free tran­son­ic flows, Mor­awetz turned to re­lated ques­tions: Can one prove ro­bust ex­ist­ence the­or­ems for weak shock solu­tions? Can one “con­tract” a weak shock to a son­ic point on the pro­file? The first ques­tion was sup­por­ted by work of Ga­rabedi­an–Korn in 1971, which demon­strated that small per­turb­a­tions of con­tinu­ous flows can have only weak shocks. The second ques­tion was in­spired by the think­ing of K. G. Guder­ley in the 1950s. Mor­awetz took two very dif­fer­ent ap­proaches to such ques­tions.

Tak­ing a sin­gu­lar per­turb­a­tion with a hodo­graph trans­form­a­tion, the ques­tions re­duce to prov­ing the ex­ist­ence of weak solu­tions to the Di­rich­let prob­lem for lin­ear mixed-type equa­tions on do­mains \( \Omega \) in the hodo­graph plane: \begin{alignat}{2} K(\sigma)\psi_{\theta\theta} + \psi_{\sigma\sigma} &= f &\quad &\text{in } \Omega,\\ \text{and }\quad \psi& =0 &\quad &\text{on } \partial\Omega, \end{alignat} where \( K(\sigma) \sim\sigma \) as \( \sigma \rightarrow 0 \). Here \( \psi \) is the stream func­tion of the flow, \( \sigma \) is a log­ar­ithmic res­cal­ing of the flow speed which is son­ic at \( \sigma = 0 \), and \( \theta \) is the flow angle. For spe­cial do­mains, Mor­awetz [Comm. Pure Ap­pl. Math. 1970] proved the sur­pris­ing res­ult of the ex­ist­ence of a unique weak solu­tion to the prob­lem.

In­spired by the dif­fer­en­cing meth­od of Jameson, Mor­awetz in­tro­duced an ar­ti­fi­cial vis­cos­ity para­met­er \( v \) in­to the non­lin­ear po­ten­tial equa­tion by re­pla­cing the (in­vis­cid) Bernoulli law \[ \rho = \rho_B (|\nabla\varphi|) \] with a first-or­der PDE which re­tards the dens­ity \( \rho \). An am­bi­tious pro­gram en­sued in or­der to prove the ex­ist­ence of weak solu­tions to the in­vis­cid prob­lem as a weak lim­it of vis­cous solu­tions. Power­ful but del­ic­ate tools in the ap­plic­a­tion of the com­pensated com­pact­ness meth­od of F. Mur­at, L. Tar­tar, and R. Di Per­na were ap­plied with suc­cess to com­plete parts of the pro­gram in Mor­awetz [Comm. Pure Ap­pl. Math. 1985, 1991] and Gamba–Mor­awetz [Comm. Pure Ap­pl. Math. 1996].

Dur­ing the peri­od 1952–2007, Mor­awetz pro­duced 22 deep re­search pa­pers and 10 sur­vey pa­pers on tran­son­ic flow and mixed-type par­tial dif­fer­en­tial equa­tions. She was an ex­em­plary fig­ure of the ap­plied math­em­atician “who proves the­or­ems to solve prob­lems.” Mor­awetz dis­covered and im­ple­men­ted a wide vari­ety of tools to handle the com­plex­ity of mixed-type PDEs. She de­veloped en­ergy meth­ods and im­port­ant iden­tit­ies by the skill­ful and in­geni­ous use of mul­ti­pli­er meth­ods cham­pioned by K. Friedrichs [Comm. Pure Ap­pl. Math. 1958] and found sur­pris­ing max­im­um prin­ciples which were cal­ib­rated to in­vari­ances in the equa­tion.

The leg­acy of Cath­leen Mor­awetz in­cludes her ded­ic­a­tion to the pro­pos­i­tion that “there is no such thing as a dis­tant re­l­at­ive,” which she ap­plied to every part of her well-lived life. Her grace, warmth and gen­er­os­ity to gen­er­a­tions of math­em­aticians work­ing in the area will be long re­membered. She was a truly in­spir­a­tion­al fig­ure who in­vited us all to “sail with her, near the speed of sound.”1