Celebratio Mathematica

Les matrices aléatoires furent considérées par Eugène Wign­er comme paradigme pour les niveaux d’éner­gie d’une large classe de systèmes quantiques. Sa vis­ion d’uni­ver­salité de ces spectres stochastiques a dépassé les espérances: les stat­istiques de matrices de Wign­er ap­par­ais­sent au­jourd’hui not­am­ment dans des do­maines tels le chaos quantique, les modèles de crois­sance, les polymères aléatoires et l’arithmétique.

Souvent, l’élar­gisse­ment de cette classe d’uni­ver­salité s’est ef­fectué via de nou­velles struc­tures intégrables, syn­onymes d’égalités en loi éton­nantes.1 À ce titre, les matrices aléatoires furent un centre d’at­trac­tion et d’ac­tion naturel pour Marc Yor. Son intérêt se doublait d’un en­viron­nement idéal au Labor­atoire de Prob­ab­ilités et de Modèles Aléatoires, en­viron­nement auquel con­tribuèrent not­am­ment Phil­ippe Bi­ane, Phil­ippe Bouger­ol, Mar­ie-France Bru, Cath­er­ine Donati-Mar­tin, Thi­erry Jeulin et Neil O’Con­nell.

Parmi les con­tri­bu­tions de Marc Yor en matrices aléatoires on peut citer par ex­emple l’ana­lyse des pro­ces­sus de Wis­hart, des tra­jectoires de matrices de corréla­tion qui généralis­ent les pro­ces­sus de Bessel. L’étude de ces pro­ces­sus mat­ri­ciels fut initiée par Mar­ie-France Bru [e10]. Dans un trav­ail com­mun avec Cath­er­ine Donati-Mar­tin, Yan Dou­merc et Hiroy­uki Mat­sumoto [7], Marc Yor a prouvé que de nom­breuses pro­priétés re­marquables des pro­ces­sus de Bessel se généralis­ent au cas Wis­hart. Par ex­emple les pro­ces­sus de Wis­hart de di­men­sions différentes véri­fi­ent des re­la­tions d’ab­solue con­tinu­ité, où ap­par­ais­sent des lois de Hart­man–Wat­son général­isées. Ces lois ont des ap­plic­a­tions en stat­istiques et mathématiques fin­ancières.

Marc Yor était aus­si motivé par l’ap­par­i­tion de stat­istiques de matrices aléatoires en théorie des nombres. Il était en par­ticuli­er ad­mir­at­if de la con­jec­ture de Keat­ing et Snaith [e14] qui lie les mo­ments de la fonc­tion \( \zeta \) le long de l’axe cri­tique à un cal­cul ana­logue pour la mesure de Haar sur le groupe unitaire. Ce cal­cul fut ini­tiale­ment ac­com­pli grâce à une for­mule de Sel­berg. Marc Yor dev­ina dans cette for­mule l’ap­par­i­tion de l’algèbre beta-gamma, ini­ti­ant ain­si une preuve géométrique et prob­ab­il­iste des intégrales de Sel­berg: le polynôme ca­ra­ctéristique de matrices aléatoires sur les groupes com­pacts classiques est un produit de vari­ables aléatoires indépendantes [8]. Ceci soulève la ques­tion d’une hy­pothétique décom­pos­i­tion ana­logue en théorie ana­lytique des nombres.

Cette note décrit un autre as­pect2 des travaux de Marc Yor en matrices aléatoires, les li­ens mystérieux avec les modèles de polymères, où ap­par­ais­sent des égalités en loi aux faux airs de simples curi­os­ités, en vérité fécondes. Plus précisément, la solu­tion d’un problème de plus long chemin en mi­lieu aléatoire (per­col­a­tion de derni­er pas­sage) est liée aux valeurs pro­pres ex­trêmes de matrices aléatoires (mouvement browni­en de Dys­on). Cette égalité en loi a eu de nom­breuses ex­ten­sions, not­am­ment une ver­sion ex­po­nen­ti­elle (i.e. à températ­ure pos­it­ive) qui est à la source d’un cer­tain nombre de pro­grès récents dans l’ana­lyse d’EDP stochastiques non linéaires.

Le tableau suivant résume des con­tri­bu­tions de Marc Yor sur ce sujet. La première est la découverte, avec Hiroy­uki Mat­sumoto, d’une contre­partie ex­po­nen­ti­elle au théorème de Pit­man: pour la première fois la pro­priété de Markov ap­paraît dans un modèle de polymère, à n’im­porte quelle températ­ure. En grande di­men­sion, Neil O’Con­nell et Marc Yor ont prouvé un résul­tat ana­logue à températ­ure nulle. Par­allèlement, ils ont in­troduit un modèle de polymère à températ­ure finie, pour le­quel Neil O’Con­nell a mon­tré une re­marquable ex­ten­sion de la pro­priété markovi­enne de Mat­sumoto–Yor. Ces modèles intégrables sont au­jourd’hui l’un des meil­leurs accès à l’ana­lyse quant­it­at­ive de l’équa­tion de Kardar, Par­isi et Zhang.

	Températ­ure 0	Températ­ure pos­it­ive
Pro­ces­sus markovi­en en	Pit­man	Mat­sumoto–Yor
petite di­men­sion
Pro­ces­sus markovi­en en	O’Con­nell–Yor	O’Con­nell
grande di­men­sion
Mesure as­sociée	Per­col­a­tion de derni­er	Polymère d’O’Con­nell–Yor
	pas­sage

Au fil des preuves des résul­tats ci-des­sus s’en­tr­emêlent physique stat­istique, mathématiques fin­ancières, grossisse­ments de fil­tra­tions, files d’at­tente, fonc­tions spéciales et systèmes intégrables, re­flétant je l’espère le chemin em­prunté par Marc Yor: la variété et la pro­fondeur de son sa­voir en cal­cul stochastique ont per­mis l’émer­gence d’iden­tités prob­ab­il­istes plus ac­tuelles que ja­mais.

Soit \( (B_t)_{t\geq 0} \) un mouvement browni­en stand­ard et \( S_t=\sup_{0\leq s\leq t}B_s \) son max­im­um. Un fameux théorème de Paul Lévy as­sure que \( (S_t-B_t)_{t\geq 0} \) est markovi­en3 Plus ex­acte­ment, ce pro­ces­sus a la même dis­tri­bu­tion que \( (|B_t|)_{t\geq 0} \), un résul­tat démon­tré habituelle­ment par l’as­tuce du prin­cipe de réflex­ion. Peut-on com­pren­dre ce ca­ra­ctère markovi­en sans cette as­tuce, stricte­ment grâce au cal­cul stochastique? Une pos­sib­ilité con­siste à in­troduire la ver­sion ex­po­nen­ti­elle du pro­ces­sus \( (S_t-B_t)_{t\geq 0} \), \[ X_t^{(\beta)}=\int_0^te^{\beta(B_s-B_t)}\,\mathrm{d} s. \] Par la méthode de Laplace, on ret­rouve \( S_t-B_t \) à partir de \( \beta^{-1}\log X_t^{(\beta)} \) quand \( \beta \) tend vers l’in­fini. La for­mule d’Itô donne \[ \mathrm{d} X^{(\beta)}_t=-\beta X_t^{(\beta)}\,\mathrm{d} B_t+(1+\beta^2 X^{(\beta)}_t/2)\,\mathrm{d} t. \] On con­clut immédiate­ment que \( (X^{\beta}_t)_{t\geq 0} \) est markovi­en, donc le pro­ces­sus \( (S_t-B_t)_{t\geq 0} \) l’est aus­si en fais­ant tendre \( \beta \) vers l’in­fini.

Fin de l’his­toire? Vraiment pas. Il ex­iste une autre com­binais­on linéaire markovi­enne de \( B \) et \( S \), comme l’a mon­tré Jim Pit­man [e3]: \[ (2S_t-B_t)_{t\geq 0}\overset{(\mathrm{ loi})}{=}(R_t)_{t\geq 0}, \] où \( R \) est un pro­ces­sus de Bessel de di­men­sion 3, c’est-à-dire la dis­tance eu­c­lidi­enne entre l’ori­gine et un point de \( \mathbb{R}^3 \) aux co­or­données browni­ennes indépendantes. Le pro­ces­sus \( R \) est aus­si un mouvement browni­en de di­men­sion 1 con­di­tionné à rest­er pos­i­tif. Il sat­is­fait l’équa­tion différen­ti­elle stochastique \( \mathrm{d} R_t=\mathrm{d} B_t+R_t^{-1}\,\mathrm{d} t \), en par­ticuli­er il est markovi­en. Parmi les com­binais­ons linéaires de \( B \) et \( S \), celles de Lévy et Pit­man sont les deux seules ay­ant cette re­marquable pro­priété [e20].

Il est tentant de sup­poser que la ver­sion ex­po­nen­ti­elle de la com­binais­on linéaire de Pit­man, \[ Z_t^{(\beta)}=\int_0^te^{\beta(2 B_s-B_t)}\,\mathrm{d} s \] est égale­ment markovi­enne. Par pro­priété de scal­ing du mouvement browni­en, on peut re­streindre l’étude à \( \beta=1 \). On peut aus­si poser la même ques­tion lor­sque \( B \) est re­m­placé par sa ver­sion avec dérive, \( B^\mu_t=B_t+\mu t \) (le théorème de Pit­man ad­met une ex­ten­sion dans cette dir­ec­tion [e7]). Mal­heureuse­ment, la for­mule d’Itô seule ne donne guère d’es­poir: \begin{equation}\label{eqn:SDE} \tag{1.1} \mathrm{d} Z_t^{\mu}=-Z_t^{\mu}\,\mathrm{d} B_t+\bigl( e^{ B_t^\mu}+\tfrac{1}{2}Z_t^{\mu}-\mu Z_t^{\mu} \bigr)\,\mathrm{d} t,\quad \mbox{où}\ Z_t^{\mu}=\int_0^t e^{2B_s^\mu-B_t^\mu}\,\mathrm{d} s. \end{equation} La méthode semble échouer, mais bizar­re­ment le résul­tat de­meure.

Les asymp­totiques de \( K_0 \) et la pro­priété de scal­ing per­mettent al­ors de montrer que le générat­eur de \( \frac{1}{\beta}\log Z_t^{(\beta)} \) con­verge vers \( \partial_{xx}/2+x^{-1}\partial_x \) sur \( \mathbb{R}_+ \), on ret­rouve donc le théorème de Pit­man. Il ex­iste désor­mais de nom­breuses démon­stra­tions du théorème de Mat­sumoto–Yor [2], [e18], [e23], y com­pris une récente in­ter­préta­tion géométrique de ce pro­ces­sus sur des es­paces symétriques de grande di­men­sion [e27]. La preuve ori­ginelle [3] est es­quissée ci-des­sous, pour soulign­er l’ex­traordin­aire di­versité des tech­niques em­ployées.

1er in­grédi­ent: pro­jec­tion d’équa­tion différen­ti­elle stochastique. Soit \( \mathcal{Z}^{\mu}_t=\sigma((Z_s^\mu)_{0\leq s\leq t}). \) On peut pro­jeter \eqref{eqn:SDE} sur la fil­tra­tion \( (\mathcal{Z}^{\mu}_t) \) (voir par ex­emple [e4]), de fa­con à ob­tenir, pour un cer­tain \( (\mathcal{Z}^{\mu}_t) \)-mouvement browni­en \( (\beta_t)_{t\geq 0} \), \[ \mathrm{d} Z_t^\mu=-Z_t^\mu\,\mathrm{d} \beta_t+\bigl(\tfrac{1}{2}-\mu\bigr)Z_t^\mu\,\mathrm{d} t+\mathbb{E}(e^{B_t^\mu}\mid (Z_s^\mu)_{0\leq s\leq t})\,\mathrm{d} t. \] Ain­si, si \( \mathbb{E}(e^{B_t^\mu}\mid (Z_s^\mu)_{0\leq s\leq t}) \) ne dépend en vérité que de \( Z_t^\mu \), al­ors le pro­ces­sus \( (Z_t^\mu) \) est markovi­en. Ceci semble peu prob­able, mais Marc Yor a rap­proché ce problème d’une iden­tité en loi au par­fum semblable.

2ème in­grédi­ent: une iden­tité re­marquable motivée par l’ac­tu­ar­iat. Il s’agit de l’ex­ten­sion, tou­jours par Mat­sumoto et Yor [3] d’un résul­tat de Daniel Du­fresne [e9] con­cernant les perpétu­ités. Ce résul­tat est le théorème 4.1 de l’art­icle de Cath­er­ine Donati-Mar­tin et Frédérique Petit dans ce volume: en not­ant \( A_t^{\nu}:=\int_0^te^{2 B_s^{\nu}}\,\mathrm{d} s \), pour tout \( \mu > 0 \) on a \[\frac{1}{A_\infty^{-\mu}}\overset{\mathrm{(loi)}}{=}2 G_{\mu},\] où \( G_\mu \) désigne une vari­able aléatoire de loi gamma de paramètre \( \mu \). Daniel Du­fresne [e17] a étendu son iden­tité en montrant que pour tout \( t > 0 \) donné, \begin{equation}\label{eqn:DMY} \tag{1.2} \frac{1}{A_t^{-\mu}}\overset{\mathrm{(loi)}}{=}\frac{1}{A_t^{\mu}}+2 G_{\mu} \end{equation} où \( G_\mu \) est indépendant du mouvement browni­en \( B \). Cette égalité à temps fixe s’étend aux pro­ces­sus, comme l’ont mon­tré Mat­sumoto et Yor [3].

3ème in­grédi­ent: grossisse­ment de fil­tra­tion. La preuve de [3] re­pose sur la très utile théorie des grossisse­ments de fil­tra­tion, large­ment déve­loppée par Jeulin [e6] et dont les premi­ers as­pects re­mon­tent à Itô [e5]. En par­ticuli­er, pour un grossisse­ment ini­tial de fil­tra­tion, on a le résul­tat suivant [1].

Si \( (\mathcal{F}_t) \) est la fil­tra­tion naturelle d’un mouvement browni­en \( B \) et \( L \) est \( \mathcal{F}_\infty \)-mesur­able, on note \( \widetilde{\mathcal{F}_t}=\mathcal{F}_t\vee\sigma(L) \). Pour toute fonc­tion \( f \) rais­on­nable, soit \[ \lambda_t(f)=\mathbb{E}(f(L)\mid\mathcal{F}_t)=\mathbb{E}(f(L))+\int_0^t\dot\lambda_s(f)\,\mathrm{d} B_s, \] où \( \dot\lambda_f(t) \) est un cer­tain pro­ces­sus prévis­ible, par re­présen­t­a­tion des mar­tin­gales. On peut aus­si écri­re \( \lambda_t(f)=\int f(x)\lambda_t(\mathrm{d} x) \) pour une cer­taine fa­mille prévis­ible de mesur­es \( (\lambda_t) \). On sup­pose que \( \dot\lambda_t(f) \) ad­met le même type de décom­pos­i­tion: \( \dot\lambda_t(f)=\int f(x)\dot\lambda_t(\mathrm{d} x) \), où \( \dot\lambda_t \) est ab­so­lu­ment con­tin­ue par rap­port à \( \lambda_t \): \( \dot \lambda_t(\mathrm{d} x)=\varrho(x,t)\lambda_t(\mathrm{d} x) \). Al­ors si \( (X_t) \) est une \( (\mathcal{F}_t) \)-mar­tin­gale sat­is­fais­ant de bonnes con­di­tions d’intégrabilité, \[ \widetilde X_t:=X_t-\int_0^t\varrho(L,s)\,\mathrm{d}\langle X,B\rangle_s \] défi­nit une \( (\widetilde{\mathcal{F}_t}) \)-mar­tin­gale.

On laisse au lec­teur le soin d’ap­pli­quer ce résul­tat pour montrer que, lor­sque \( L=A^{-\mu}_\infty \), le nou­veau pro­ces­sus \[ \widetilde B_t=B_t-\int_0^t\biggl(\frac{e^{2B_s^{-\mu}}}{A_\infty^{-\mu}-A_s^{-\mu}}-2\mu\biggr)\,\mathrm{d} s \] est un \( (\widetilde{\mathcal{F}_t}) \) mouvement browni­en, indépendant de \( A_{\infty}^{-\mu} \). La résolu­tion de cette équa­tion d’in­con­nue la fonc­tion \( B \) donne \[ B_t-\mu t=\widetilde B_t+\mu t-\log(1+\widetilde A_t^{(\mu)}/A_\infty^{-\mu}) \] pour tout \( t\geq 0 \). En ap­pli­quant \( f\mapsto \int_0^te^{2f(s)}\,\mathrm{d} s \) à ces deux fonc­tions on ob­tient, pour tout \( t\geq 0 \), \[ \biggl(\frac{1}{A_t^{-\mu}}\biggr)_{t\geq 0}=\biggl(\frac{1}{\widetilde A_t^{(\mu)}}+\frac{1}{A_\infty^{-\mu}}\biggr)_{\!t\geq 0}. \] Ceci con­clut la preuve de \eqref{eqn:DMY}, car \( \widetilde B \) est indépendant de \( A_\infty^{-\mu} \), de dis­tri­bu­tion voulue grâce à Du­fresne.

4ème in­grédi­ent: une équa­tion stochastique fonc­tion­nelle. On peut donc dériver \eqref{eqn:DMY} en \( t \) pour ob­tenir, con­jointe­ment avec la valeur en \( +\infty \), \[ \biggl(\biggl(\frac{1}{(Z_t^{-\mu})^2}\biggr)_{\!t\geq 0},\frac{1}{A_\infty^{-\mu}}\biggr)\overset{\mathrm{ (loi)}}{=} \biggl(\biggl(\frac{1}{(Z_t^{\mu})^2}\biggr)_{\!t\geq 0},2 G_\mu\biggr). \] En par­ticuli­er, \( (Z_t^{-\mu}))_{t\geq 0} \) est indépendant de \( A_\infty^{-\mu} \).

Soit désor­mais \( X \) une vari­able aléatoire de loi celle de \( \exp(B_t^{-\mu}) \) con­di­tion­nelle­ment à \( \mathcal{Z}_t^{-\mu} \) et \( Z_t^{-\mu}=z \). En util­is­ant l’indépendance précédente et la décom­pos­i­tion élémen­taire \[ A_\infty^{-\mu}=e^{B_t^{-\mu}}Z_t^{-\mu}+(e^{B_t^{-\mu}})^2\int_t^\infty e^{2(B_s^{-\mu}-B_t^{-\mu})}\,\mathrm{d} s, \] on ob­tient fa­cile­ment une équa­tion fonc­tion­nelle stochastique sat­is­faite par \( X \): \[ (2 G_\mu)^{-1}X^2+z\, X\overset{\mathrm{ (loi)}}{=}(2 G_\mu)^{-1}, \] où \( G_\mu \) et \( X \) sont indépendants. La résolu­tion de cette équa­tion fonc­tion­nelle pe­met d’ob­tenir \[ \mathbb{E}(e^{B_t^{-\mu}}\mid (Z_s^{-\mu})_{s\leq t})=(K_{\mu+1}/K_\mu)(1/Z_t^{-\mu}). \] Des ma­nip­u­la­tions de fonc­tions de Bessel–Mac­don­ald con­clu­ent al­ors la preuve du théorème de Mat­sumoto–Yor pour une dérive négat­ive, résul­tat étendu à tout \( \mu \) par pro­longe­ment ana­lytique, par ex­emple.

Les con­nec­tions entre problèmes de plus court (ou long) chemin en di­men­sion deux et valeurs ex­trêmes de valeurs pro­pres de matrices aléatoires sont ap­par­ues dans [e12], où Baik, Deift et Jo­hans­son ont mon­tré le résul­tat suivant. Soit \( \ell(N) \) la lon­gueur de la plus longue sous-suite crois­sante d’une per­muta­tion uni­forme de \( [\![ 1,N]\!] \). Al­ors pour tout réel \( t \) \begin{equation}\label{TW1} \tag{2.1} \lim_{N\to\infty}\mathbb{P}\biggl(\frac{\ell(N)-2\sqrt{N}}{N^{1/6}}\leq t\biggr)=\mathrm{ F}_\mathrm{ TW}(t), \end{equation} où \( \mathrm{ F}_\mathrm{ TW} \) est la fonc­tion de répar­ti­tion de la loi de Tracy et Wi­dom, qui peut s’exprimer à l’aide des solu­tions d’équa­tions de Pain­levé II [e11].

Cette loi est ap­par­ue ori­ginelle­ment dans un con­texte de matrices aléatoires. Soit en ef­fet \( H_N \) une matrice her­mi­tienne de taille \( N\times N \), telle que \( (H_N)_{ii} \), \( \sqrt{2}\mathbb{R}e(H_N)_{ij} \) et \( \sqrt{2}\Im(H_N)_{ij} \) (\( i > j \)) sont gaussi­ennes indépendantes, de vari­ance \( 1/N \). Ce modèle de matrices aléatoires in­troduit par Wign­er est naturel, il est es­sen­ti­elle­ment unique­ment ca­ra­ctérisé par l’indépendance des en­trées et l’in­vari­ance par con­ju­gais­on unitaire. Si on or­donne les valeurs pro­pres de \( H_N \), \( \lambda_1\leq \dots\leq \lambda_N \), al­ors on a aus­si la con­ver­gence \begin{equation}\label{TW2} \tag{2.2} \lim_{N\to\infty}\mathbb{P}(N^{2/3}(\lambda_N-2)\leq t)=\mathrm{ F}_\mathrm{ TW}(t). \end{equation} Cette oc­cur­rence de la même loi dans un problème de plus court chemin \eqref{TW1} et de matrices aléatoires \eqref{TW2} a été depuis véri­fiée dans de nom­breux autres ex­emples (par ex­emple ce li­en est prouvé dans [e13] pour un modèle plus réal­iste de plus long chemin sur \( \mathbb{Z}^2 \)).

Il semble fructueux de recherch­er une ex­ten­sion tem­porelle aux li­ens ci-des­sus. Par ex­emple, le modèle dy­namique classique de matrice aléatoire gaussi­enne suivant fut in­troduit dans [e2]: chaque en­trée de la matrice her­mi­tienne \( H_N \) est désor­mais un mouvement browni­en com­plexe cor­recte­ment nor­malisé, les valeurs pro­pres restent or­données (\( \lambda_i(t) < \dots < \lambda_N(t) \) pour tout \( t > 0 \)) et sat­is­font l’équa­tion différen­ti­elle stochastique autonome suivante, le mouvement browni­en de Dys­on: \[ \mathrm{d}\lambda_k(t)=\frac{\mathrm{d} B_k(t)}{\sqrt{N}}+\frac{1}{N}\sum_{i\neq k}\frac{1}{\lambda_k(t)-\lambda_i(t)}\,\mathrm{d} t, \] où \( B_1,\dots B_N \) sont des mouve­ments browni­ens indépendants. Cette dy­namique de \( \boldsymbol{\lambda}=(\lambda_1,\dots,\lambda_N) \) co­in­cide avec celle de mouve­ments browni­ens indépendants con­di­tionnés à de­meurer dans \( C_N=\{\boldsymbol{\lambda}\in\mathbb{R}^N:\lambda_1\leq\dots\leq\lambda_N\} \): le générat­eur in­fin­itésim­al est (à change­ment d’échelle près) \[ \frac{\Delta}{2}+\nabla\log h\cdot\nabla \] où \( h(\boldsymbol{\lambda})=\prod_{1\leq i < j\leq N}(\lambda_i-\lambda_j) \) est har­mo­nique dans \( C_N \). Ex­iste-t-il un modèle dy­namique de per­col­a­tion de derni­er pas­sage de loi \( (\lambda_N(t))_{t\geq 0} \)?

Pour ex­hiber un tel modèle, considérons de nou­veau \( B_1(t), \dots,B_N(t), t\geq 0 \) une col­lec­tion de \( N \) mouve­ments browni­ens indépendants, dont les ac­croisse­ments sont notés \( B_k(s,t)=B_k(t)-B_k(s) \). La vari­able aléatoire \begin{equation}\label{eqn:prob} \tag{2.3} M_t^N=\max_{0\leq s_1\leq \dots\leq s_{N-1}\leq t}(B_1(s_1)+B_2(s_1,s_2)+\dots+B_N(s_{N-1},t)) \end{equation} re­présente la solu­tion d’un problème d’op­tim­isa­tion du type derni­er pas­sage: le plus long chemin entre \( (0,0) \) et \( (t,N) \) pour un march­eur dont les seuls pas autor­isés sont dis­crets vers le nord, pour un coût nul, ou con­tinus vers l’est, pour un coût gaussi­en in­fin­itésim­al.

Pour \( t \) fixé, les vari­ables aléatoires \( M_t^N \) et \( \lambda_t^N \) sont identique­ment dis­tribuées, comme l’ont mon­tré Bary­sh­nikov [e15], Gravn­er, Tracy and Wi­dom [e16]. La ver­sion dy­namique de ce résul­tat ap­paraît sim­ul­tanément dans les travaux de Bouger­ol et Jeulin [e19] (dans un con­texte de chambres de Weyl plus général) et ceux d’O’Con­nell et Yor [6]. À l’oc­ca­sion de leur étude, ces derniers ont in­troduit une ver­sion du problème \eqref{eqn:prob} à températ­ure ar­bit­raire, décrite dans la prochaine partie.

Aupara­v­ant, pour énon­cer leur résul­tat à températ­ure zéro, on aura be­soin des trans­form­a­tions suivantes. Pour toutes fonc­tions càdlàg sur \( \mathbb{R}_+ \) nulles à l’ori­gine, on défi­nit \[ (f\otimes g)(t)=\inf_{0\leq s\leq t}(f(s)+g(t)-g(s)),\quad (f\odot g)(t)=\sup_{0\leq s\leq t}(f(s)+g(t)-g(s)). \] En l’ab­sence de par­enthèses, l’or­dre des opéra­tions est de gauche à droite (par ex­emple \( f\odot g\otimes h=(f\odot g)\otimes h \)). On défi­nit aus­si la trans­formée \( \Gamma_2(f,g)=(f\otimes g,g\odot f) \) et ses itérés: \[ \eqalign{ \Gamma_k(f_1,&\dots,f_k) \cr& =\bigl(f_1\otimes f_2\otimes\dots\otimes f_k, \Gamma_{k-1}( f_2\odot f_1,f_3\odot(f_1\otimes f_2),\dots,f_k\odot(f_1\otimes\dots\otimes f_{k-1}) ) \bigr)} \] Si \( \Gamma_N({\mathbf B})_1 \) désigne la première com­posante de \( \Gamma_N({\mathbf B}) \), ob­tenue lor­sque \( f_1=B_1,\dots, f_N=B_N \) sont des mouve­ments browni­ens indépendants is­sus de 0, al­ors \[ \Gamma_N({\mathbf B})_1(t)=\min_{0\leq s_1\leq\dots\leq s_{N-1}\leq t}(B_1(s_1)+B_2(s_1,s_2)+\dots+B_N(s_{N-1},t)). \] Par symétrie, \( -\Gamma_N({\mathbf B})_1 \) est dis­tribué comme le pro­ces­sus \( M^N \).

Ce résul­tat cor­res­pond, quand \( N=2 \), au théorème de Pit­man. En ef­fet, d’un côté \( R:=(\lambda_2-\lambda_1)/\sqrt{2} \) est un mouvement browni­en con­di­tionné à rest­er pos­i­tif, i.e. un pro­ces­sus de Bessel en di­men­sion 3. D’un autre côté, un cal­cul donne \[ \Gamma_2(f_1,f_2)_2-\Gamma_2(f_1,f_2)_1=2m-x \] où \( x=f_2-f_1 \) et \( m(t)=\max_{0\leq s\leq t} x(s) \).

La preuve du théorème re­pose sur la maîtrise et l’ap­pro­fon­disse­ment de résul­tats de files d’at­tente. On se donne \( \mathrm{ N}_1,\dots,\mathrm{ N}_N \) les fonc­tions de comptage de pro­ces­sus de Pois­son indépendants sur \( \mathbb{R}_+ \), d’in­tens­ités re­spect­ives \( \mu_1 < \dots < \mu_N \). O’Con­nell et Yor ont mon­tré le résul­tat suivant.

La ver­sion Pois­son (O’Con­nell–Yor [6]) La loi con­di­tion­nelle de \( \mathrm{ \mathbf N}=(\mathrm{ N}_1,\dots,\mathrm{ N}_N) \) sachant \( \mathrm{ N}_1(t)\leq \dots\leq \mathrm{ N}_N(t)) \) pour tout \( t\geq0 \) est la même que la loi, in­con­di­tion­nelle, de \( \Gamma_N(\mathrm{ \mathbf N}) \).

On ret­rouve les li­ens entre mouvement browni­en de Dys­on et per­col­a­tion de derni­er pas­sage quand \( \mu_1,\dots,\mu_N \) con­ver­gent vers une même in­tens­ité, puis en ap­pli­quant le théorème de Don­sker.

Pour com­pren­dre le résul­tat ci-des­sus con­cernant les pro­ces­sus de Pois­son, re­gar­dons le cas \( N=2 \), lié aux files d’at­tente de type \( M/M/1 \). Celles-ci sont con­stru­ites à partir de deux pro­ces­sus de Pois­son \( A \) et \( S \) sur \( \mathbb{R} \) d’in­tens­ités re­spect­ives \( 0 < \lambda < \mu \). On note \( \chi(t)=\chi(0, t] \) pour tout pro­ces­sus ponc­tuel \( \chi \). Soit \begin{align*} Q(t)&=\sup_{s\leq t}(A(s,t]-S(s,t])_+,\quad t\in\mathbb{R},\\ D(s,t]&=A(s,t]+Q(s)-Q(t). \end{align*} En ter­mes de file d’at­tente, le pro­ces­sus \( A \) re­présente les ar­rivées, \( S \) le ser­vice, \( Q \) le nombre de cli­ents dans la queue et \( D \) le pro­ces­sus des départs. Le théorème de Burke [e1] est le résul­tat suivant.

Théorème de Burke. \( D \) est un pro­ces­sus de Pois­son d’in­tens­ité \( \lambda \).

Une preuve de ce résul­tat est très simple et re­pose sur la révers­ib­ilité de \( Q \): celle-ci im­plique que la loi de \( (A,D) \) est la même que celle de \( (\overline{D},\overline{A}) \), où on défi­nit \( \overline{\chi}(s,t)=\chi(-t,-s) \). En par­ticuli­er, \( \overline{D} \) est un pro­ces­sus de Pois­son d’in­tens­ité \( \lambda \), donc \( D \) aus­si. O’Con­nell et Yor ont trouvé l’ex­ten­sion suivante, simple et très utile, où l’on note \( U=S-D \) le pro­ces­sus de ser­vice non util­isé et \( T=A+U \).

Ex­ten­sion du théorème de Burke. (O’Con­nell–Yor [6]) Les pro­ces­sus \( D \) et \( T \) sont des pro­ces­sus de Pois­son indépendants d’in­tens­ités re­spect­ives \( \lambda \) et \( \mu \).

En ef­fet, pour \( Q \) donné, \( U \) est un pro­ces­sus de Pois­son d’in­tens­ité \( \mu \) sur \( \{t: Q(t)=0\} \). Si \( V \) est indépendant de \( U \) con­di­tion­nelle­ment à \( Q \), Pois­son d’in­tens­ité \( \mu \) sur \( \{t: Q(t)\neq0\} \), al­ors \( N=U+V \) est Pois­son d’in­tens­ité \( \mu \) sur \( \mathbb{R} \) indépendant de \( Q \). Le couple \( (A,S) \) est fonc­tion de \( (Q,N) \): \( (A,S)=f(Q,N) \). Al­ors par con­struc­tion \( (\overline{D},\overline{T})=f(\overline{Q},\overline{N}) \). Par révers­ib­ilité de \( Q \) et \( N \), \( (\overline{D},\overline{T}) \) a la même loi que \( (A,S) \), donc \( (D,T) \) aus­si.

L’ex­ten­sion du théorème de Burke donne une preuve limp­ide de la ver­sion Pois­son du théorème, quand \( N=2 \): la loi de \( (A(t),S(t))_{t\geq 0} \), étant donné \( A(t)\leq S(t) \) pour tout \( t\geq0 \), est la même que celle de \( (D(t),T(t))_{t\geq 0} \) sachant \( Q(0)=0 \). Mais si \( Q(0)=0 \), al­ors \( (D(t),T(t))=\Gamma_2(A,S)(t) \) pour tout \( t\geq 0 \). De plus les ac­croisse­ments de \( A \) et \( S \) sont indépendants, donc \( (\Gamma_2(A,S)(t))_{t\geq 0} \) est indépendant de \( Q(0) \). La loi de \( (A(t),S(t))_{t\geq 0} \) étant donné \( A(t)\leq S(t) \) pour tout \( t\geq0 \) est donc la même que celle, in­con­di­tion­nelle, de \( (\Gamma_2(A,S)(t))_{t\geq 0} \).

L’ex­ten­sion du théorème de Burke donne donc en par­ticuli­er une ver­sion Pois­son du théorème de Pit­man, ain­si qu’une preuve élémen­taire de ce derni­er.

La preuve de la ver­sion Pois­son pour \( N \) général re­pose sur une récur­rence et des ar­gu­ments semblables à ceux ci-des­sus.

Les polymères di­rigés en mi­lieu aléatoire furent in­troduits par Huse et Haley [e8]. Ils ont une dir­ec­tion dite tem­porelle im­posée et sont libres de bouger dans les autres di­men­sions. Le poids de Boltzmann donne la prob­ab­ilité de ret­rouver le polymère dans une cer­taine con­fig­ur­a­tion, il s’exprime à l’aide d’un hamiltoni­en qui dicte l’éner­gie d’une tra­jectoire \( \pi \): \[ \mathrm{d} \mathbb{P}_\mathrm{ Q}(\pi)=\frac{1}{Z^{(\beta)}_\mathrm{ Q}}e^{\beta H(\pi)}\,\mathrm{d} \mathbb{P}_0(\pi), \] où \( \beta \) est la températ­ure in­verse, \( \mathbb{P}_0 \) une mesure sur les chemins indépendante du hamiltoni­en \( H \) et des aléas qui le défin­is­sent. L’in­dice Q men­tionne qu’il s’agit d’une loi de type quenched, c’est-à-dire dépendant du choix du mi­lieu aléatoire.

Le croise­ment des résul­tats de Mat­sumoto–Yor et d’O’Con­nell–Yor suggère que cer­tains modèles de polymères, à températ­ure ar­bit­raire, pour­raient s’in­ter­préter comme com­posantes de dif­fu­sions markovi­ennes de di­men­sion finie. Cette idée fut ren­forcée par la découverte d’ana­logues de la pro­priété de Burke [5] dans le cas de modèles de type Mat­sumoto–Yor. En par­ticuli­er, dans [5] O’Con­nell et Yor in­troduis­ent le modèle de polymère avec fonc­tion de par­ti­tion \[ Z^{(N,\beta)}_t=\int_{0 < s_1 < \dots < s_{N-1} < t}e^{\beta(B_1(s_1)+B_2(s_1,s_2)+\dots+B_N(s_{N-1},t))}\,\mathrm{d} s_1\dots\mathrm{d} s_{N-1}, \] où \( B_1,\dots, B_N \) sont des mouve­ments browni­ens indépendants. Parmi les nom­breux résul­tats con­cernant ce modèle, les asymp­totiques de l’éner­gie libre (\( \lim_{N\to\infty}N^{-1}\log Z^{(N,\beta)}_t \)) peuvent être cal­culées [5], [e22], ain­si que ses fluc­tu­ations [e30]. Pour com­pren­dre ses fluc­tu­ations jointes en \( t \), peut-on in­ter­préter ce polymère comme co­or­donnée d’un pro­ces­sus de Markov ex­pli­cite, de façon sim­il­aire à la partie précédente (\( \beta=\infty \))?

Neil O’Con­nell a récem­ment ap­porté une belle réponse à cette ques­tion: les iden­tités en loi de Marc Yor n’ont pas fini d’être éten­dues et in­flu­entes. Pour décri­re le résul­tat prin­cip­al de [e24], on défi­nit au préal­able \( \phi \), un chemin nord/est comme une ap­plic­a­tion crois­sante et sur­ject­ive de \( [0,t] \) and \( [\![ 1,N]\!] \), dont les sauts ont lieu à des in­stants \( s_1 < s_2 < \dots < s_{N-1} \). On util­ise l’abrévi­ation \[ E(\phi)=B_1(s_1)+B_2(s_1,s_2)+\dots+B_N(s_{N-1},t) \] et on peut im­poser \( \beta=1 \) sans perte de généralité, par scal­ing browni­en. Le polymère d’O’Con­nell–Yor cor­res­pond à la première co­or­donnée (\( n=1 \)) du modèle \[ Z^{(N)}_{n,t}=\int_{D_n(t)}e^{\sum_{i=1}^n E(\phi_i)}\,\mathrm{d} \phi_1\dots\mathrm{d}\phi_n, \] où \( D_n(t) \) est l’en­semble des \( n \)-up­lets de chemins \( (\phi_1,\dots,\phi_n) \) dis­joints, démar­rant à \( (0,1),\dots,(0,n) \) et fin­is­sant en \( (t,N-n+1),\dots,(t,N) \). La mesure \( \mathrm{d} \phi_1\dots\mathrm{d}\phi_n \) est la mesure de Le­besgue sur le do­maine eu­c­lidi­en \( D_n(t) \).

On défi­nit al­ors \[ X_{n,t}^N=\log\biggl(\frac{Z_{n,t}^N}{Z_{n-1,t}^N}\biggr). \]

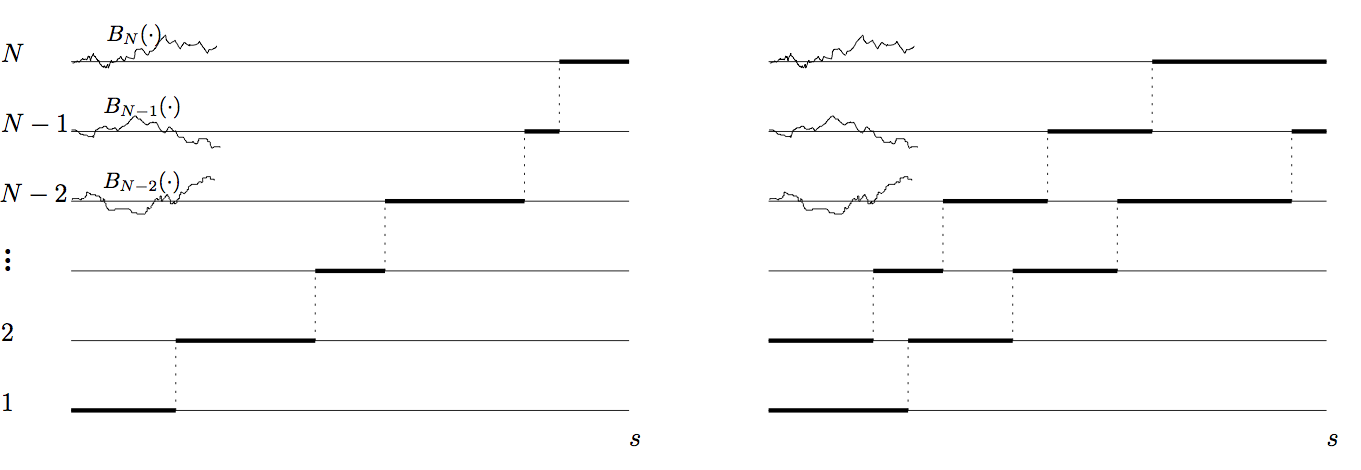
Le polymère d’O’Con­nell–Yor est donc ob­tenu via une trans­formée de Doob du mouvement browni­en. Il est im­possible dans cette note de soulign­er de façon com­plète l’in­flu­ence de ces modèles de polymères (en par­ticuli­er leur ca­ra­ctère markovi­en). Voici néan­moins quelques avancées sig­ni­fic­at­ives très récen­tes que l’on peut situer dans la généalo­gie de Mat­sumoto–Yor.

1. Le polymère d’O’Con­nell–Yor con­verge, après une bonne nor­m­al­isa­tion, vers la solu­tion de l’équa­tion KPZ au sens Hopf–Cole, c’est-à-dire le log­ar­ithme de la solu­tion de l’équa­tion de la chaleur stochastique (avec comme con­di­tion ini­tiale un Dir­ac) [e29].
2. Cette con­ver­gence a ain­si per­mis de montrer que la solu­tion de l’équa­tion de Kardar Par­isi et Zhang (tou­jours au sens précédent, avec une con­di­tion ini­tiale spéci­fique) hérite de la re­la­tion d’ab­solue con­tinu­ité du pro­ces­sus d’O’Con­nell par rap­port à la mesure de Wien­er [e26].
3. Ch­haibi [e25] a général­isé le théorème précédent à une grande classe de groupes de Lie. Pour cette théorie générale qui im­plique trans­form­a­tion de Pit­man géométrique, théorie des re­présen­t­a­tions et cristaux géomet­riques, voir [e21], [e25].
4. Rider et Valkó ont en­tre­pris l’ex­ten­sion des résul­tats de Du­fresne, Mat­sumoto et Yor pour des pro­ces­sus mat­ri­ciels de type Wis­hart [e28].